1. Introducción
Los módulos Fotovoltaicos (FV) están constituidos por la unión de varias células solares, que a su vez son la base de la energía solar fotovoltaica, esto nos ayuda a generar energía eléctrica de manera limpia, renovable y segura para abastecer la demanda creciente de energía eléctrica que tenemos en nuestros hogares y edificios [1]. La energía FV está creciendo continuamente de acuerdo con estudios realizados por IRENA (Agencia de Energía Renovable Internacional) [2]. Hecho que hace que aumente su presencia en el mundo energético con 175.3 GW instalados al final de 2014, según demuestran los estudios hechos por IRENA [3].
En este trabajo se estudia el comportamiento de la tecnología FV con el objetivo de mejorar su funcionamiento, y para ello hay que considerar sus pérdidas energéticas. El interés principal de este trabajo es estudiar las pérdidas por reflectancia en la corriente debidas a la desviación angular del rayo de incidencia respecto a la normal de la superficie de los generadores fotovoltaicos.
Las pérdidas angulares se definen como la variación relativa de la corriente eléctrica generada por un módulo FV bajo una radiación incidente a un ángulo de incidencia respecto del valor obtenido a esa misma irradiancia a la incidencia normal [1].
En este documento se cuantifican las pérdidas angulares que se producen en los módulos FV trabajando en condiciones reales, comparando distintas tecnologías comerciales FV y teniendo en cuenta el comportamiento de los módulos con un grado de suciedad.
Las pruebas se han desarrollado en la unidad de energía solar fotovoltaica del Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas (CIEMAT), que está ubicada en el edificio 42. Se trabajó con medidas tomadas con: un piranómetro, un módulo FV y una célula normalizada para estudiar los efectos de reflectancia en los módulos fotovoltaicos situados en el exterior, en la terraza del edificio.
Es importante medir las pérdidas por reflexión en la ganancia de corriente debida a la desviación angular del rayo de la incidencia respecto a la normal de la superficie de los generadores fotovoltaicos, en condiciones reales ya que al medir en interior con una lámpara no tendremos todo el campo del espectro solar, y además la luz está más colimada y se evitan errores de no homogeneidad de la iluminación.
La versión original del arreglo experimental, contaba con una plataforma giratoria donde estaban montados los instrumentos (célula fija, módulo fotovoltaico y piranómetro), primero se orientaba manualmente poniéndola en una posición normal al sol, después haciendo un barrido de 180º grados valiéndose de un transportador para conocer los ángulos de inclinación, al mismo tiempo con un multímetro se iban anotando los datos manualmente conforme se iba girándola plataforma manualmente, esto hacia que para esta tarea se tuviera que realizar con mínimo dos personas, una que estuviera girando la plataforma y otra que estuviera anotando los datos.
Observamos que se podía mejorar el ensayo trabajando en la automatización del movimiento de la plataforma, esto se hará colocando un potenciómetro conectado al eje transversal, esto nos dará una señal en ohmios que capturaremos en un datalogger, después con un algoritmo que diseñamos, leeremos esa información para controlar dos relés que están conectados de forma que controlemos un motor DC para hacer girar la plataforma.
2. Fundamentos teóricos
2.1 Electricidad FV generada
Plantas con la misma capacidad de potencia máxima pueden tener diferencias importantes en la producción de energía; debido principalmente a la irradiación recibida por los módulos fotovoltaicos, hecho que depende de las condiciones ambientales del sitio.
Normalizado la irradiancia específica a una de referencia de 1 kW/m2, se define el rendimiento de referencia (Yr) (reference yield) y se expresa en unidades de horas [4], magnitud que permite la comparación del número efectivo de horas de sol pico en cada caso.
Generalmente, la productividad de una instalación fotovoltaica conectada a la red se calcula sobre la base anual y es caracterizada por la productividad final del sistema (YF), que es la energía generada por el sistema normalizado por el pico de potencia instalada (kWh/kWp) y se entiende como el número efectivo de horas de producción de la planta. Por ejemplo, en España la producción de plantas fotovoltaicas en horas reales en generadores fijos instalados de más de una década normalmente varía desde 900 a 1200 kWh/kWp mientras que los valores en el Reino Unido por lo general varían de 300 a 650 kWh/kWp la diferencia en los rendimientos de la plantas FV se debe principalmente a las diferencias de productividades de referencia (recurso solar), en menor grado a la diferencia de rendimiento del sistema.
2.2. El rendimiento global
El Performance Ratio (PR), o rendimiento global o característico de un sistema fotovoltaico, es la relación entre la productividad final del sistema y la productividad de referencia [4], y compara la energía generada con lo que se produciría con la misma cantidad de irradiación, pero en condiciones ideales sin pérdidas. Por lo general las pérdidas FV son debidas al generador FV, espectro solar, reflexión angular, suciedad en la cara, cableado y otras ineficiencias de los componentes del sistema FV. Aunque algunas de estas pérdidas deben calcularse por hora, por lo menos debemos suministrar un valor integrado anual para calcular la relación de rendimiento y así:
PR = (1 - L temperatura )·(1 - L suciedad )·(1 - L angulares )·(1 - L inversor ) (1 - L cableado )... (Ec. 1)
Dónde:
Ltemperatura: pérdidas por temperatura
Lsuciedad: pérdidas por suciedad
Langulares: pérdidas angulares
Linversor: perdidas por los inversores
Lcableado: pérdidas por el cableado
El PR nos sirve para encontrar la eficiencia de un sistema FV, independientemente de la eficiencia del módulo. El PR anual de los sistemas FV es aproximadamente 0.8 con tendencia al alza desde alrededor de 0.7 en 80s [5].
2.3. El concepto de pérdidas
El concepto de pérdidas en este ámbito de la generación de la energía se refiere a unas condiciones reales, con ello tendremos todo el campo de irradiación del espectro solar, por el contrario anteriormente en este ensayo se intentaba reproducir la irradiancia del espectro solar con el uso de una lámpara por lo tanto solo conseguían parte de campo irradiación del espectro solar [6].
En general, se analizan las pérdidas de corriente y a su vez las pérdidas de potencia se analizan a partir de éstas mediante un factor de proporcionalidad que es dependiente de la tecnología del módulo [6].
2.4. La reflectancia ponderada
Los módulos fotovoltaicos producen corriente fotogenerada, esta además de depender de la radiación incidente, es función de la reflectancia y de su repuesta espectral, S(λ). En principio, todos los materiales que constituyen los módulos son dispersivos [7], con lo que las características ópticas del conjunto dependerán de la longitud de onda de la radiación incidente. Por lo tanto usaremos la reflectancia R(λ) y transmitancia T(λ) espectrales, las cuales dependen a su vez del ángulo de incidencia.
La respuesta espectral es una función que es fuertemente dependiente de la longitud de onda, y débilmente dependiente de ángulo de incidencia, además para longitudes de onda altas, solo resulta significativo el aumento de recorrido medio óptico del haz de luz dentro del material activo de la célula inducidos por ángulos de incidencia altos, sin embargo estos ángulos ya no son tan altos cuando llegan al material de la célula, debido a la cubierta de vidrio en el módulo [8].
Entonces, al considerar la respuesta espectral del módulo dependiente exclusivamente de la longitud de onda, se conviene para trabajar con valores de reflectancia ponderada por el producto de estas funciones por la distribución espectral de la radiación, E(λ), que se tomará como estándar ignorando por el momento los cambios espectrales de la luz. Esta reflectancia ponderada, simbolizada por ˉR (Ecuación 2) [8].
La Ecuación (2) nos da una idea del comportamiento angular global de módulo, ya que al integrarla considerando los límites de integración de la respuesta espectral en cuestión, que normalmente para el silicio son de 300 nm y 1200 nm, resulta solo función del ángulo de incidencia (α).
3. Desarrollo del proyecto
3.1. Pérdidas angulares
La obtención de pérdidas angulares en el estudio del comportamiento angular bajo radiación directa se obtiene mediante la expresión [8]:
Donde el subíndice B indica que la radiación incidente es directa y no hay componente difusa. Esta expresión se refiere a la transmisión angular con relación a la situación de incidencia normal [8].
Las pérdidas angulares se definen como la variación relativa de la corriente generada por un módulo bajo una radiación incidente a uno o más ángulos de incidencia respecto del valor obtenido a la incidencia normal.
Para la obtención de pérdidas las angulares, en el estudio del comportamiento angular de un módulo en condiciones reales usaremos la ecuación siguiente [8]:
Dónde:
α es el ángulo de incidencia.
Ics(α) es la corriente de cortocircuito en la posición de ángulo de incidencia.
Isc(0) es la corriente de cortocircuito en la posición normal al sol.
La Ecuación (4) muestra el cálculo del cociente en corto circuito a un ángulo determinado y su valor a incidencia normal, corregido por el factor de coseno de la reducción de la irradiancia con el ángulo.
3.2. Ensayo con el potenciómetro para su calibración en función del ángulo
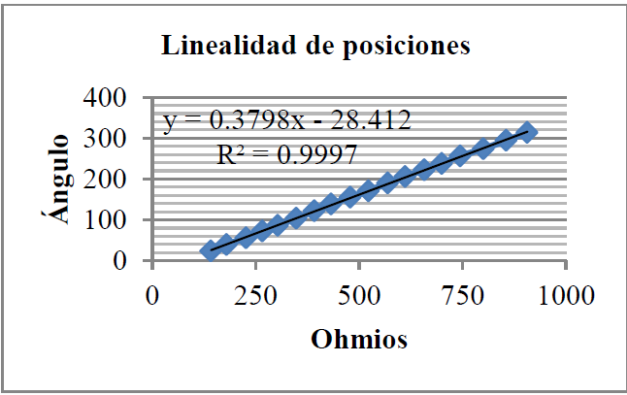
Para poder automatizar el movimiento transversal de la plataforma giratoria donde se colocaran los instrumentos de medida, se tuvo que instalar unido al eje trasversal un potenciómetro de 1000 ohmios con tornillo sin fin multivuelta con una tolerancia de linealidad de ± 0.25 %., Este dispositivo entrega una señal en ohmios que después registramos, para conocer la resistencia en cada punto de giro se obtuvo la línea de tendencia (5) que nos ayudó para ajustar el control de la posición de la plataforma.
La ecuación de la línea de tendencia mostrada en la Figura 2 se incorporara a un algoritmo para controlar los movimientos de la plataforma.
3.3. Montaje experimental del módulo FV para ensayos y medidas
Se colocaron sobre la plataforma los siguientes dispositivos para probar su respuesta en condiciones reales: un módulo FV de silicio multicristalino (Si-m), un módulo de lámina delgada de silicio amorfo con 30 % de transparencia (Si-a 30 %) y un piranómetro CMP11 el cual utiliza la tecnología de detector de temperatura compensada.

Figura 3 Detalle del: ii) piranómetro CMP11 y iii) minimódulo de silicio multicristalino en el equipo de medidas.

Figura 4 Montaje de instrumentos sobre el eje de la plataforma (v), al fondo se observa parte de la estructura de aluminio.
Después se colocó una estructura hecha con perfiles de aluminio de 1 pulgada formando una estructura cúbica liviana y resistente sobre la plataforma. Se fijó esta con el fin de servir de soporte para colocar sobre ella una tela negra muy gruesa para evitar que llegara la luz que se refleja en los instrumentos.

Figura 5 Plataforma giratoria para sujeción de los módulos a ensayar. iv) Se observa el mecanismo mediante un tornillo y una manivela para orientar los módulos hacia el sol de manera correcta.

Figura 6 Montaje del armazón cúbico para después tapar los laterales para evitar la radiación difusa y reflejada a los módulos y el piranómetro.
Por último, se fijó a la estructura cúbica, una tela oscura y gruesa para proteger los paneles y el piranómetro de la luz reflejada y la difusa, por reflejo del piso, para que no afecte a las medidas del experimento de pérdidas angulares.
4. Montaje del sistema completo
Para hacer el diseño eléctrico se tuvo que investigar las características de los componentes. Para ello se consultaron sus hojas de características de datos.
4.1 Diseño eléctrico
Después de conocer las características de los componentes se continuó con el diseño de la automatización de la plataforma. Para ello, primero se diseñó el circuito eléctrico para conectar un datalogger Agilent 34970A que es un recolector de datos, tiene un barrido de 60 canales de 2 a 4 hilos y además se puede conectar remotamente mediante comandos SCPI. En este dispositivo se pueden introducir hasta 3 multiplexores. Se utilizó la tarjeta 34901A porque tiene 20 canales con switch de uso general y la tarjeta Agilent 34903A que cuenta con 20 relés independientes. A estas tarjetas se les conectaron los dispositivos de medida (potenciómetro, piranómetro CPM11), y los módulos fotovoltaicos (Si-a 30 %) y célula de referencia (Si-m) según se muestra en la Figura (8).
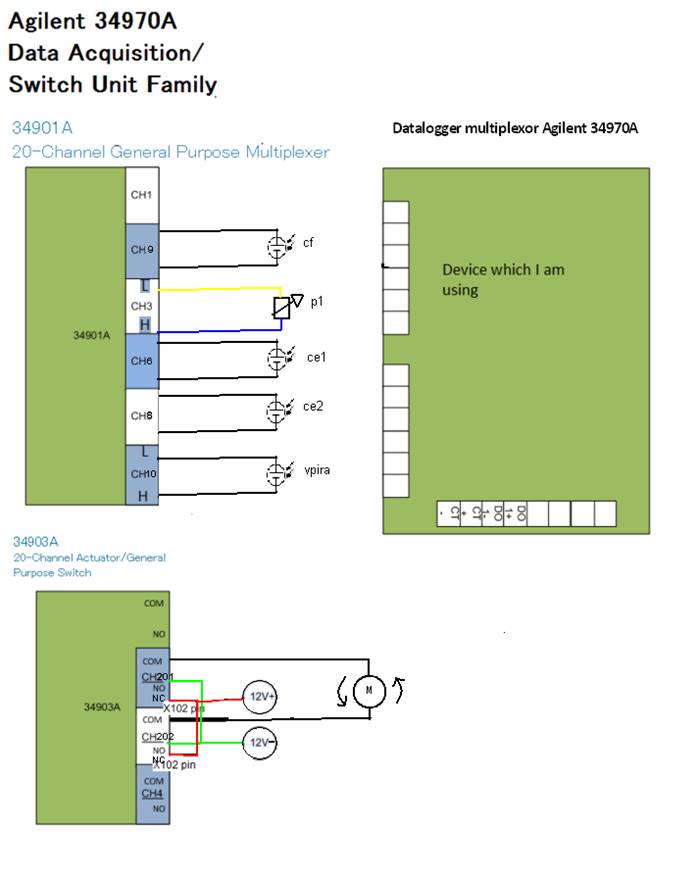
Figura 8 Circuito eléctrico diseñado para conectar el datalogger y las tarjetas con los dispositivos de medida, donde cf es la célula fija, ce1 es la célula de ensayo 1, ce2 célula de ensayo 2, p1 el potenciómetro y vpira el piranómetro.
Se conectó el potenciómetro de 1000 ohmios ligado al eje transversal de la plataforma. Esto nos dio una señal en ohmios que se capturó en el datalogger. Se utilizó esta señal para ajustar la línea de tendencia (5) y conocer la posición de la plataforma giratoria.
A continuación, se diseñó un programa en Matlab para que registrara la señal de salida del potenciómetro. Usando esa información controlamos dos relés que están conectados entre sí, de tal forma que se pueda controlar el arranque, paro y cambio de giro del motor, que moverá la plataforma mientras el sistema toma los datos y los va almacenado en la memoria interna del ordenador.
4.2 Descripción del programa de control de la plataforma y adquisición de datos
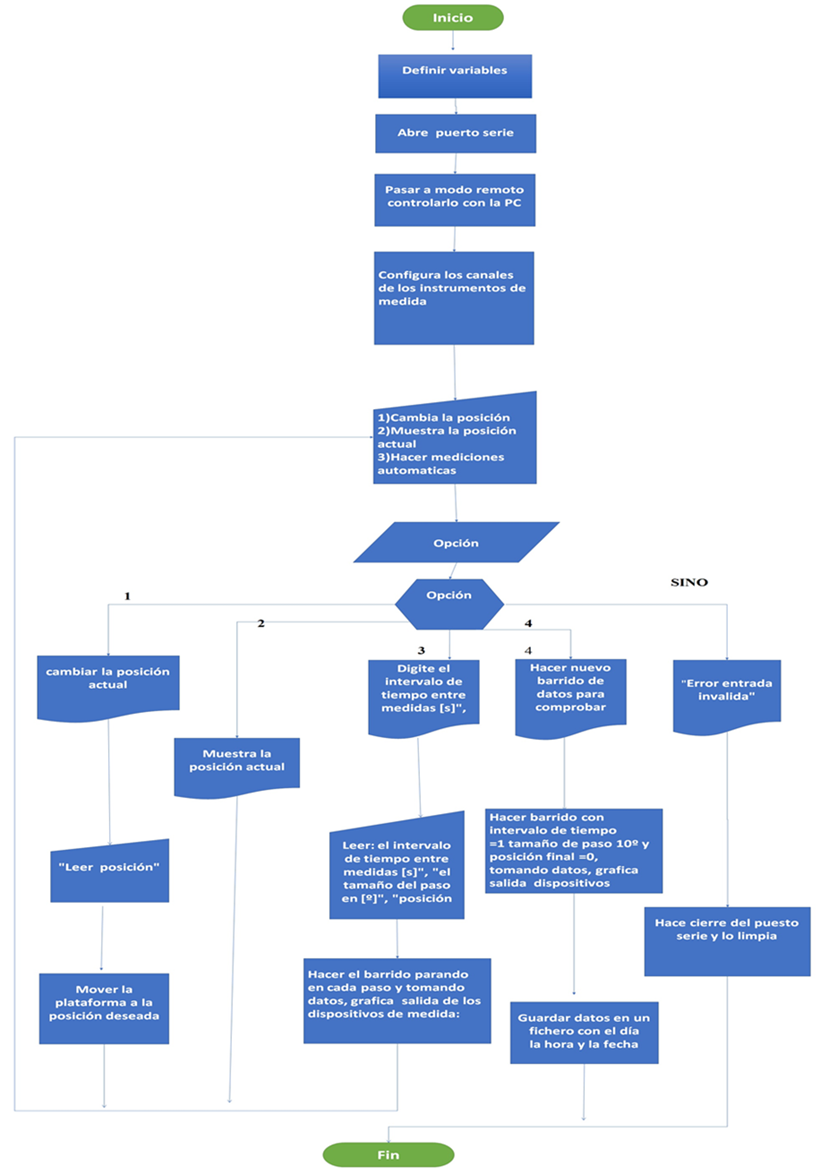
El programa de control de la plataforma y adquisición de datos lleva a cabo las siguientes tareas, en el Anexo 1 se muestra el diagrama de flujo:
Primero establece el tipo de variables que son las señales de los instrumentos.
Abre el puerto serie del ordenador.
Manda una instrucción al datalogger para pasar a modo remoto y controlarlo con el PC.
Configura los canales para medir la salida de los instrumentos a medir.
Abre una cadena de ciclos o bucles, lee la salida del potenciómetro y ajusta la salida.
Después muestra el siguiente menú: 1) cambiar la posición actual 2) no 3) desea hacer mediciones automáticas 4) salir.
La opción 1 nos permite mover la plataforma al lugar donde nos convenga iniciar las mediciones teniendo una apertura de 320 grados.
Una vez colocado en posición, podemos seleccionar en el menú la opción 3) para hacer mediciones automáticas. Nos pedirá que le proporcionemos lo siguiente:
El intervalo de tiempo entre medidas (en segundos), el tamaño del paso (en grados). La posición final del barrido.
El programa tomará los parámetros que le introducimos, empezará a hacer el barrido e irá parando en cada paso y tomando datos. Al mismo tiempo va haciendo una gráfica en tiempo real de la salida de los dispositivos de medida de forma automática como las mostradas a continuación.
El programa tiene mecanismos de seguridad para que en caso de poder ingresar un valor no válido, éste automáticamente detecte un error y se salga del programa, cierre el puerto serie y lo limpie para evitar errores al intentar comunicarse nuevamente.
Una vez que el programa ha terminado el ciclo, podemos elegir la opción 4) salir del programa.
El programa vuelve a hacer un barrido ahora con un intervalo de tiempo de 1 tamaño de paso de 10º y posición final = 0. Representa gráficamente la salida de dispositivos de medidas de la célula fija, célula de ensayo 1, célula de ensayo 2, potenciómetro y piranómetro.
Cierra el puerto serie.
Finalmente guardamos los datos para analizarlos.
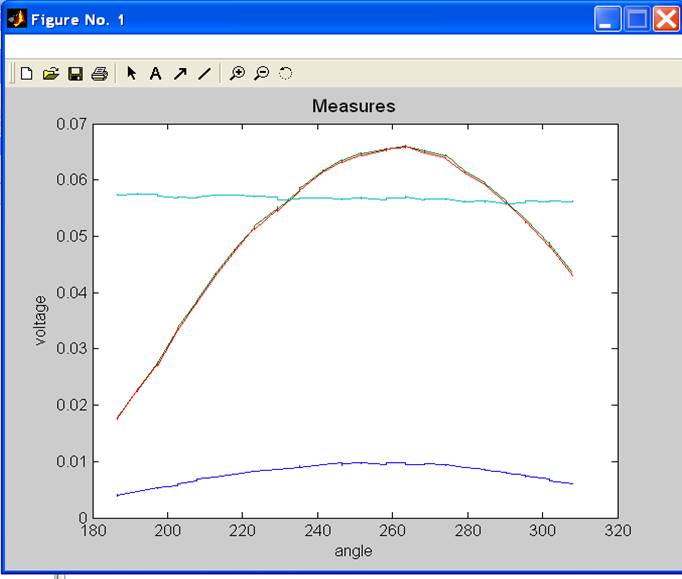
Figura 9 Respuesta de la salida de los instrumentos en tiempo real en un día despejado próximo al medio día solar, en función del ángulo de incidencia, línea azul claro: célula fija, línea roja: célula de ensayo, 1 silicio multicristalino y línea azul oscuro: piranómetro.
4.3. Registro de datos y medidas de la corriente generada durante periodos cercanos al mediodía en días despejados en función del ángulo de incidencia
Una vez que todos los dispositivos están preparados y orientados correctamente, se le da la instrucción al programa para que gire la plataforma en pequeños pasos de 5º y en cada paso haga una pausa de 5 segundos para hacer 5 mediciones por cada dispositivo (una medición por cada segundo), esto para comparar cada medida 5 veces, y al final del ciclo completar un barrido de 180º. Una vez que el programa hizo las mediciones automáticas, se exportaron los datos a Excel para facilitar su estudio.
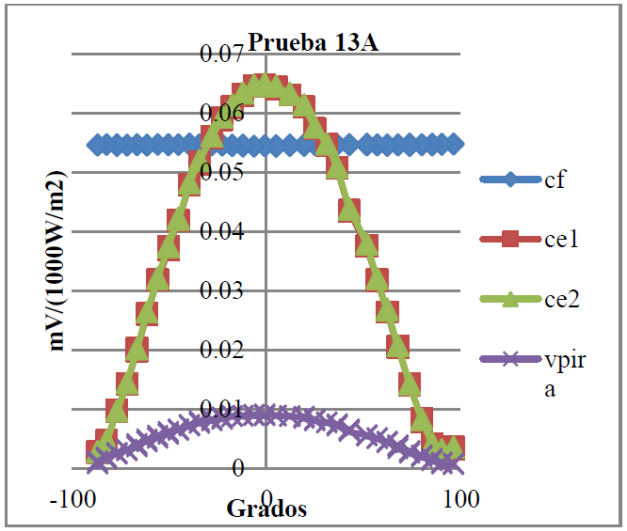
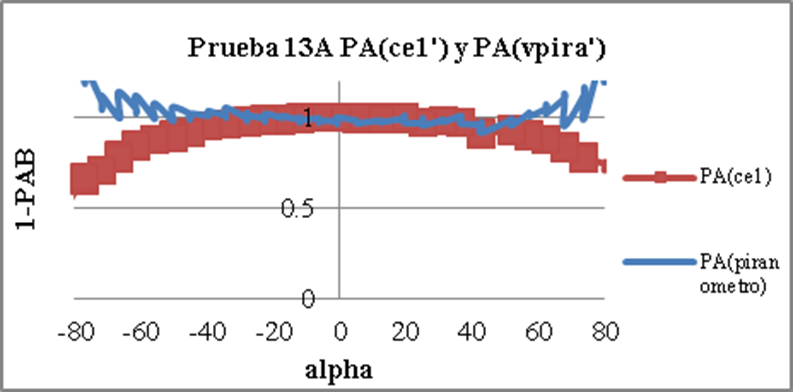
Figura 11 Respuesta de la salida de los instrumentos en un día despejado próximo al mediodía solar, en función del ángulo de incidencia donde cf: célula fija, ce1: célula de ensayo 1 ce2: célula de ensayo 2 y vpira: piranómetro.
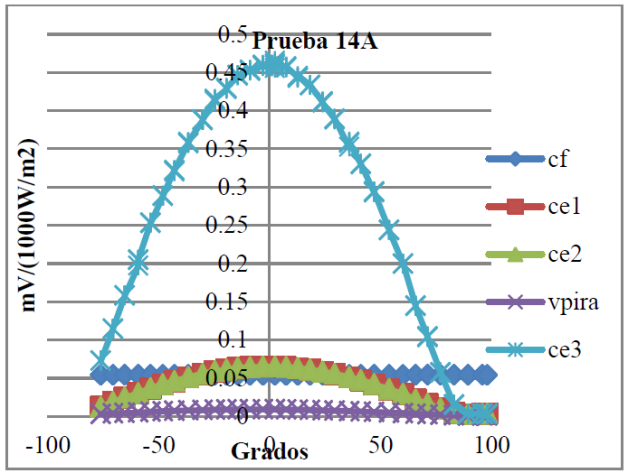
Figura 12 Repuesta de la corriente generada por los módulos en un día despejado. Se muestra la comparación del minimódulo (ce1 ce2) con la salida del módulo de lámina delgada (ce3).
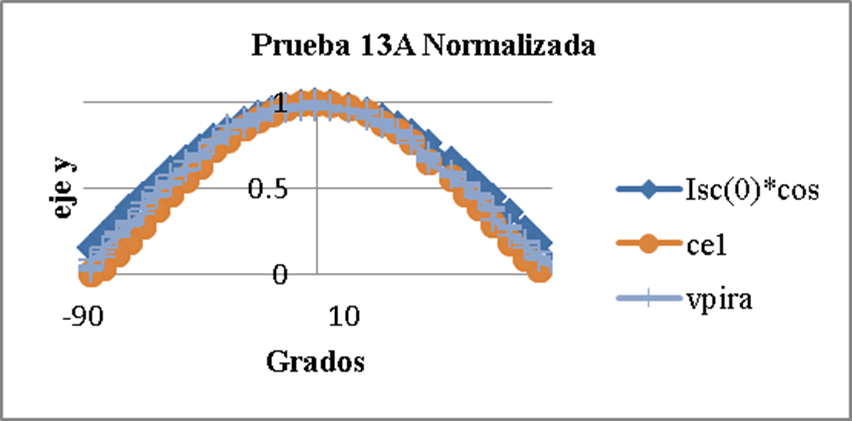
Figura 13 Comparación de las curvas de respuestas normalizadas Isc(0)*cos(α) del módulo, la ce1 (célula de ensayo 1) y el vpira (voltaje del piranómetro). Se puede observar que los valores de la célula de ensayo y del piranómetro se encuentran por debajo de Isc(0)*cosα.
Los datos muestran simultáneamente la medida de las curvas I-V de las células de ensayo. También se ha registrado la irradiancia siempre medida en posición perpendicular a la dirección del haz de luz solar en condiciones reales, y siempre medida con una célula de referencia calibrada. A partir de los valores de la corriente de cortocircuito (ISC) de las células, corregidos por temperatura y normalizados a una misma irradiancia, se han calculado las pérdidas angulares en cada caso. Esto se ha realizado mediante el factor angular definido en la Ecuación (4) es decir, cálculo del cociente de corto circuito a un ángulo determinado y su valor a incidencia normal, corregido por el factor de coseno de la reducción de la irradiancia con el ángulo.
4.3. Modelo analítico de la reflectancia de un módulo FV
4.3.1 Modelo Martin-Ruiz
Se usará el modelo Martin-Ruiz [8] que utiliza una función que ajusta lo mejor posible al comportamiento observado. Este modelo ha sido recientemente adoptado en la Norma IEC 61853-2:2016 [9].
La reflectancia ponderada es una función monótona creciente del ángulo de incidencia, que toma valor mínimo a 0º (incidencia normal) y el máximo a +/- 90°, que es la unidad, la siguiente es la expresión del modelo
Dónde ar es un parámetro empírico a determinar en cada caso, directamente relacionado con las pérdidas angulares (“coeficiente de pérdidas angulares”), definidas por la expresión (4) y determinadas con el último factor de la Ecuación (6.0).
El término exp(-1/ar) es comúnmente muy pequeño en comparación con la unidad, pero se añade por coherencia matemática esto hace que se cumplan las condiciones de contorno:
PAB(α = 0º) = 0
PAB(α = 90º) = 0
4.3.2 Modelo ASHRAE
Se ha utilizado también el modelo denominado ASHRAE, que fue desarrollado para captadores solares [10] y posteriormente adoptado por ASHRAE (American Society of Heating, Refrigeration, and Air Conditioning Engineers) [11].
La expresión del factor angular, 1-PAB resulta lo siguiente:
Nota: tiene una singularidad este modelo y por ello no puede ajustarse los datos hasta 90 grados, esta es una dificultad por ello hemos considerado ángulo hasta 80º.
Simulación de los modelos matemáticos
Para simular y obtener los parámetros de los modelos se utiliza el programa SPSS que es un programa estadístico. Tomamos los datos obtenidos en el registro de datos de las pruebas 13A y 14 B, los exportamos a este programa, después aplicamos una regresión no lineal para los Martin-Ruiz y el modelo ASHRAE, con las Ecuaciones (6.1 y 7) para obtener los parámetros ar y b0 respectivamente, los cuales mostraremos en la Tabla (1).
Tabla 1 Resultados de los ajustes de las pérdidas angulares de módulos de diferentes tecnologías a los modelos matemáticos.
| Modelo | C. | P. | Tec. | Valor estimado | σ relativo | r2 | |
|---|---|---|---|---|---|---|---|
| 13A | Martin- Ruiz [7] (hasta 80º) (Ec. 6.1) | ce1 | ar | Si-m (sucia) | 0,247 | 7,00E-03 | 0,921 |
| ce2 | ar | Si-m | 0,244 | 6,00E-03 | 0,932 | ||
| 14B | ce1 | ar | Si-m (limpia) | 0,212 | 6,00E-03 | 0,902 | |
| ce2 | ar | Si-m | 0,209 | 6,00E-03 | 0,917 | ||
| ce3 | ar | Si-a 30% transp. | 0,303 | 5,00E-03 | 0,988 | ||
| 13A | ASHRAE[9] (hasta 80º) (Ec. 7) | ce1 | b0 | Si-m | 0,069 | 3,00E-03 | 0,800 |
| ce2 | b0 | Si-m | 0,068 | 3,00E-03 | 0,819 | ||
| 14B | ce1 | b0 | Si-m | 0,073 | 3,00E-03 | 0,848 | |
| ce2 | b0 | Si-m | 0,073 | 3,00E-03 | 0,865 | ||
| ce3 | b0 | Si-a 30% transp. | 0,11 | 3,00E-03 | 0,943 |
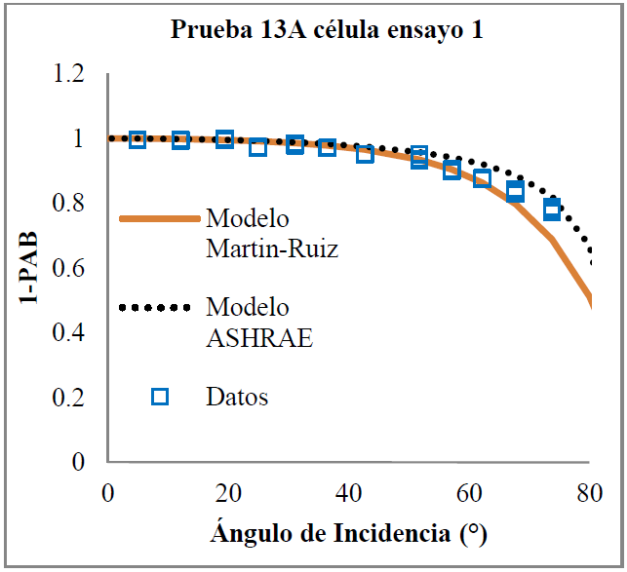
Figura 15 Práctica número 13A célula de ensayo número 1, tecnología Si-m, datos de la corriente de cortocircuito relativa a incidencia normal (puntos) y curva ajustada según el modelo Martín-Ruiz y el ASHRAE considerando los datos correspondientes hasta 80º.
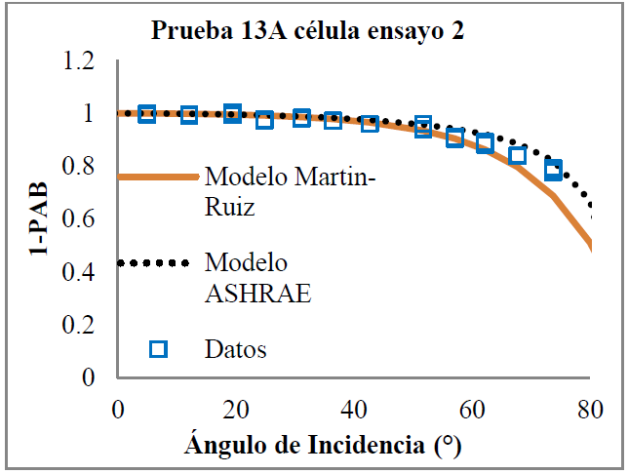
Figura 16 Práctica número 13A célula de ensayo número 2, tecnología Si-mc, datos de la corriente de corto circuito relativa a la incidencia normal (puntos) y curva ajustada según el modelo Martín-Ruiz y el ASHRAE considerando los datos correspondientes hasta 80º.
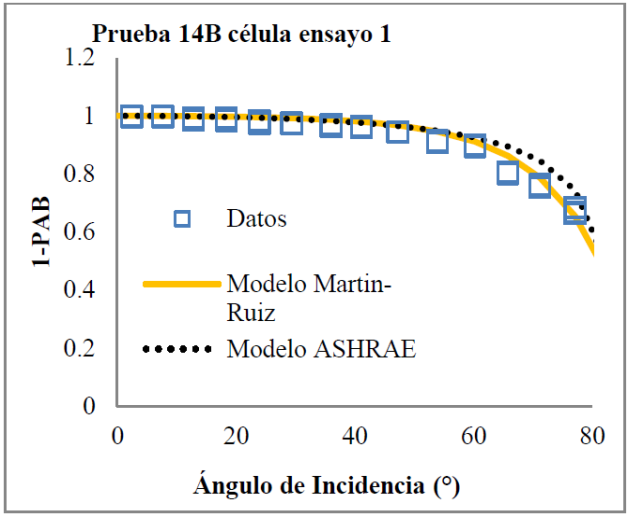
Figura 17 Práctica 14A célula de ensayo número 1, tecnología Si-m, datos de la corriente de cortocircuito relativa a incidencia normal (puntos) y curva ajustada según el modelo Martín-Ruiz y el ASHRAE considerando los datos correspondientes hasta 80º.
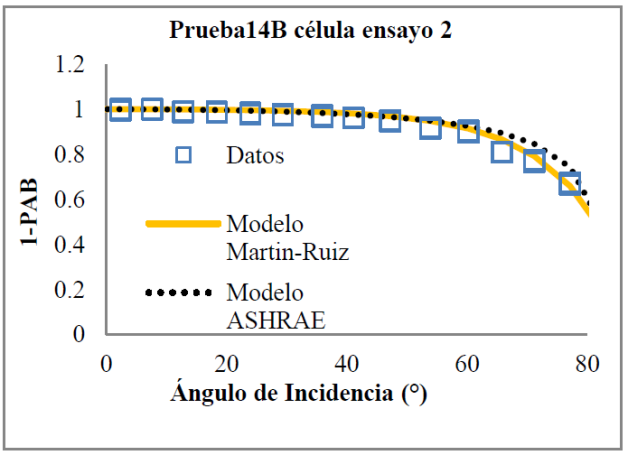
Figura 18 Práctica 14A célula de ensayo número 2, tecnología Si-mc, datos correspondientes a la corriente de cortocircuito relativa a incidencia normal (puntos) y curva ajustada según el modelo Martín-Ruiz y el ASHRAE considerando los datos correspondientes hasta 80º.
5 Resultados obtenidos
La Tabla 1 muestra los resultados de ajustar los datos de las pruebas a las ecuaciones de los modelos matemáticos Martin-Ruiz y ASHRAE, para ángulos de incidencia de hasta 80º, en intervalos de 5°. Se muestra el valor estimado del parámetro de ajuste, su error asintótico típico (σ) relativo y el coeficiente de determinación de la regresión, obtenidos utilizando el programa estadístico SPSS.
En todos los casos el ajuste obtenido es bueno, aunque en las pruebas 13A y 14B los mejores ajustes son los obtenidos con el modelo Martin-Ruiz, según indican los valores de σ y r².
El valor del parámetro de pérdidas del modelo Martin-Ruiz a r oscila entre 0,21 y 0,25 aproximadamente, siendo comparativamente mayor en los casos de suciedad superficial que en los de superficie limpia.
El valor del parámetro de pérdidas del modelo ASHRAE oscila entre 0,07 y 0,11. Al igual que en el otro modelo, mayores valores del parámetro de pérdidas, en este caso b 0, indican mayores pérdidas angulares. También se cumple que la suciedad incrementa el valor de las pérdidas angulares.
Los máximos valores de pérdidas en ambos casos se obtienen con el módulo de silicio amorfo. Puede haber influido que el módulo sea semitransparente y el color de la estructura de soporte es blanco. Esto provoca que a incidencia normal se aproveche mejor la irradiancia reflejada que los casos de incidencia oblicua.
6. Conclusiones
Se concluye a la vista de los resultados que el proyecto de automatización de ensayo de reflectancia angular de módulos fotovoltaicos en el exterior ha tenido un buen desempeño, porque el método de toma de datos funciona de manera adecuada para estudiar el comportamiento de los módulos FV, piranómetro y la célula de calibración.
Este proyecto funciona bien para medir diferentes tecnologías de módulos FV. En este estudio se probaron un mini-módulo fotovoltaico con 2 células de silicio multicristalino y un módulo de tecnología de lámina delgada de silicio amorfo, pero también sería válido para otros dispositivos de diferentes materiales, como por ejemplo monocristalinos, células de heterounión, y otros dispositivos de lámina delgada como CdTe y Cu(GaxIn1-x)Se2, entre otros.
Como se muestra en los resultados en la Tabla (1) podemos observar buenos ajustes con los dos modelos de comportamiento angular considerados, aunque en general, en los casos estudiados, los mejores parámetros de ajuste son los obtenidos con el modelo de Martin-Ruiz.
Podemos observar que el modelo Martin-Ruiz (Ec. 6.1), describe las curvas de reflectancia angular ponderada, mediante los parámetros de la reflectancia a incidencia normal ˉR(0) y ar que es el coeficiente de pérdidas angulares. Este describe el comportamiento angular relativo del módulo, el cual muestra que al aumentar este coeficiente empeora el comportamiento angular del módulo (pérdidas mayores).
Se observa en los coeficientes de pérdidas angulares ar de la Tabla (1) que para el caso de la célula de ensayo de Si-a (ce3) son notablemente mayores que los del mini-módulo (ce1 y ce2), y por esto se puede concluir que tiene mayores pérdidas angulares. Puede haber influido que el módulo sea semitransparente y el color de la estructura de soporte es blanco. Esto provoca que a incidencia normal se aproveche mejor la irradiancia reflejada que los casos de incidencia oblicua.
La tecnología que se ajusta mejor a los modelos matemáticos para obtener los parámetros de las pérdidas angulares en este proyecto es la del ensayo 3 (ce3) de la prueba 14B, que corresponde al módulo de silicio amorfo con un 30 % de transparencia, como se puede apreciar en la Tabla (1).
Este proyecto nos ayuda a estudiar mejor las perdidas angulares, las cuales en aplicaciones FV de integración en edificios, sobre todo en las fachadas, tienen una gran importancia.











 text new page (beta)
text new page (beta)