text new page (beta)
English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Similars in
SciELO 
Permalink
1 Introduction
The Quadratic Assignment Problem (QAP) is a discrete optimization problem in particular of combinatorial optimization and consists of finding an optimal assignment of n facilities to n localities with the purpose of minimizing the cost of transportation, given two matrices, a matrix of distances between the localities and another with the flow of materials between the facilities.
Note that each facility can only be assigned to one location and each location can only accept one facility, that is, it is a one-to-one relationship. The distance and material flow matrices are symmetric. What is required is that the facilities with the highest flow of materials are as close as possible in order to minimize the cost of transportation. The QAP solutions posed as a combinatorial optimization problem are permutations, observe in figure 1 the solution of that assignment is 2413 which represents the assignment of facility 2 to city A, 4 to city B,1 to city C and the 3 to the city D.
On the other hand, [13] mentions that the QAP is one of the most difficult problems of the NP-hard class and the motivation for its study is the number of applications that can be found in: logistics areas, operations research, combinatorial analysis and data in computer science, in order to reinforce the theoretical importance of the study of QAP.
Additionally, in [13] it is stated about some problems posed as QAP among these are the following: Traveling Salesman Problem, Bin Packing, Maximal Clique, Isomorphism and Graph Partitioning [13]. A survey for the quadratic assignment problem presents an analysis of 362 publications which the 95% are directly related to QAP.
The QAP was proposed by [11] as a mathematical model for the allocation of economic activities.
In 1976 Shani and González proved that QAP is an NP-hard problem [24, 25] where it is shown that for problems of this class there is no exact algorithm that can solve them in a polynomial order time.
So far, only optimal solutions have been found using exact methods for instances of size less than 30 [23, 26]. QAP appears in many applications, such as computer keyboard design, manufacturing programming, airport terminal design, and communications processes, among others. The most popular exact algorithm to solve the QAP is the branch and bound [24] algorithm with some variants: the first exact parallel branch and bound algorithm was proposed by [26]. However, in recent years it has been proposed its solution through different approximation techniques called metaheuristics for the QAP [20, 18], among these are: Ant Colony (ACO), Artificial Neural Networks (NN), Genetic Algorithms (GA), Scatter Search (SS), Annealing Simulated (SA), Tabu Search (TS) [26] and Greedy Randomized Adaptive Search Procedure (GRASP) [14, 15] among others. Another technique [19, 21] implemented GRASP in parallel for QAP.
The major drawbacks that heuristic techniques face is the existence of local optimum that are not absolute. If during the search there is a local optimum, the heuristic could not continue the process and would be “trapped” at the same point. In order to solve the problem, it is recommended to restart the search from another initial solution and verify that the new search explores other paths [2, 3].
Most combinatorial optimization problems are specific problems, so a heuristic technique algorithm that works for one problem is sometimes not useful for solving other problems. However, in recent years, general purpose heuristics called metaheuristics have been developed that try to solve the above drawbacks. Most metaheuristics are developed with neighborhood search methods [2, 3].
GRASP is an iterative procedure where each step consists of a construction phase and an improvement phase. In the construction phase, a constructive heuristic procedure is applied to obtain a good initial solution. This solution is improved in the second phase by a local search algorithm. The best of all the solutions examined is the final result [16, 23].
The main contribution of this research is to find solutions for SQAP through the implementation of the metaheuristic Greedy Randomized Adaptive Search Procedure (GRASP), in the JAVA programming language. The document is divide as follows. Section 1 contains an introduction, in section 2, the related work is presented, section 3, the formulation of QAP is given, after this in section 4, the GRASP methodology is described, in section 5, the SQAP is stated, in the section 6, all the results are presented. Finally, in section 7, the conclusion and future work is presented.
2 Related Works
The QAP is a combinatorial optimization problem that consists in finding an optimal allocation of n resources to n locations in order to minimize the cost of transportation. A matrix of requirements for units to be transported and the cost of transport per unit between the localities is given.
There are as many techniques and applications to solve the QAP as the one proposed by [25] that includes the solution of real problems using multiobjective optimization of ant colonies for the QAP.
Furthermore, other algorithms such as the hybrid artificial bee colony [6] are an efficient metaheuristic for the QAP solution, which promises to be a good candidate to obtain an optimal solution with large instances for these intractable problems.
Although metaheuristics are used for solving complex and real-world problems, they do not provide an exact solution, but only an approximate solution like [12] that use the combination of different neighborhood structures to make an improvement in the implementation for QAP.
Furthermore, in [26, 27] it is stated that genetic algorithms and taboo search metaheuristics can provide near optimal solutions for large QAP instances that require a reasonable time to complete.
Since metaheuristics are not specific to a problem, it is interesting to determine which metaheuristics is best suited for each type of problem.
The word metaheuristics was coined by [2] at the same time that the term Tabu Search emerged (1986).
A metaheuristic is a master strategy that guides and modifies other heuristics to generate better solutions than are normally presented by other methods [26].
There are several successful metaheuristics in solving combinatorial problems. The GRASP metaheuristic is one of the most recent techniques, it was originally developed by [11] at the time of studying coverage problems of high combinatorial complexity [3]. Each iteration in GRASP generally consists of two steps: the build phase and the local search procedure. In the first stage, an initial solution is built that is later improved by post-processing to perfect the solution obtained in the first stage until obtaining a local optimum.
The metaheuristic procedures are a class of approximation methods, designed to solve difficult combinatorial optimization problems, where the classical heuristics are neither effective nor efficient, much less the exact methods [10].
Metaheuristics have the virtue of obtaining solutions close to the optimum in a reasonable computation time with respect to the size of the problem using moderate computational resources.
This article presents the design of a GRASP metaheuristic for QAP and applied to Stochastic Quadratic Assignment Problem (SQAP) where the test instances were taken and modified from the QAPLIB library [22].
Optimization problems are based on choosing the best configuration from a set of feasible solutions to achieve an objective [12]. Optimization problems are divided into two categories: problems with continuous and discrete variables, for the case of the first group a set of real numbers or a function is sought, while in the second it is generally intended to find an objective that is taken within a finite and discrete set, an integer, a set of integers, a permutation, or a graph. The two types of problems have different methods of solving; however, combinatorial optimization problems belong to the second category [12] as an example, GRASP
3 Formulation of the Quadratic Assignment Problem
The QAP consists of finding an optimal allocation that minimizes the cost of transporting materials, among n facilities in n locations, considering the distance between locations and the flow of materials between facilities. The QAP can be formulated by a combinatorial optimization model (CP).
Given a set
where
The QAP can also be posed as an integer programming problem as follows:
where X is a matrix of binary variables, tr is the trace of the matrix, with the matrix F and D symmetric.
For our application, the flow matrix F is a stochastic non-symmetric matrix and D is the distance matrix which remains symmetric, with which, the objective function of the problem loses the previous integer programming trace structure but retains the combinatorial optimization structure.
4 General GRASP Methodology
The GRASP design has been used by some researchers to solve the QAP for different instances [15] and with other applications such as: building blocks which are common to other metaheuristics, GRASP with path- relinking and their different strategies for the efficient implementation, path relinking for balancing reconfigurable transfers lines [5, 8, 9, 25], multi-mode transportation planning of crude oil via GRASP and path relinking [25] and hybridization of GRASP with data mining [3].
There are applications of GRASP in experimental investigation to study the probability and distribution of solution time [1].
Probabilistic stopping rules for GRASP heuristics and extensions that propose stopping rules based on the tradeoff between solution quality and the time needed to find a solution that might improve the solution are discussed in [23].
A GRASP metaheuristic to improve accessibility after disaster, in which the problem considers the allocation of scarce resources to repair a rural road network after a natural disaster with the purpose of maximizing the accessibility of as many people as possible to the main cities or regional centers, where the economic and social infrastructure usually is located, is presented in [7].
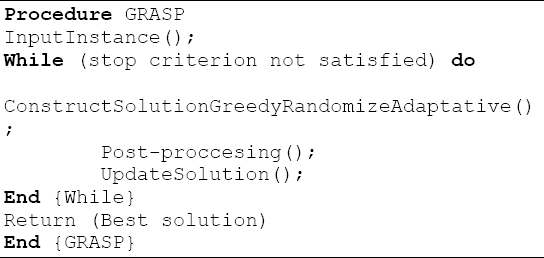
GRASP is an iterative process; each iteration consists of two steps: the construction phase and the local search procedure. In the first, an initial feasible solution is built, later it is improved by means of an exchange procedure until obtaining a local optimum [4].
Once the two phases have been executed, the solution obtained is stored and another iteration is carried out, each time saving the best solution that has been found so far. Algorithm 1 exemplifies the aforementioned metaheuristics.
The GRASP overview has three main components. The first is the Greedy component that uses a myopic algorithm for the selection of the components that guide the construction of solutions.
The second is that the Randomized used for the random selections from an elite list of candidates that determine the search path.
Finally, the Adaptive component has the mission of updating each result obtained from the components of the solution that is built.
4.1 Implementation for the Quadratic Assignment Problem
The GRASP design has been used by some researchers to solve the QAP for different instances [15, 4, 6]. The construction phases for QAP are as follows.
Construction phase, Stage 1. The two initial assignments are made simultaneously, specifically it will be said that resource i is assigned to location k and resource j is assigned to location l, when the cost corresponding to this pair of assignments is
Let α, β, (0 < α, β <1) be the parameters that restrict the list of candidates (RLC),
Let
Subsequently, the distance and flow entries are listed in increasing and decreasing order respectively, that is:
Now, two ordered lists are obtained, therefore, the parameter
The last list is ordered in increasing order using the parameter α to obtain the definitive restricted list of candidates (RLC). Using the RLC, only the first
In this way, the random component of the method is appreciated, and the first stage of the construction phase concludes.
Stage 2. It is intended to complete the initial solution by calculating the n-2 remaining assignments, through an avid procedure that produces one by one the assignments that have the least cost with respect to the existing assignments. In the event of a tie, it will be broken randomly and relying on an adaptive component in charge of updating the solution as it is being built.
Let
the set of assignments under construction. Stage 2 starts with
Let
the cost of assigning factory i to location k with respect to existing assignments.
Subsequently, the unassigned pairs (i, k) that have the minimum cost
In this part, there is also an RLC where the
The function of the adaptive component of GRASP is to update the set Γ by adding new assigned pairs, that is:
At the end of this stage, the first phase also concludes, therefore, a solution has been built contained in the set:
Ordering the first components of the pairs, the second components are taken to form the permutation equivalent to the solution [14].
Post processing phase: stage 2. The mission of the phase is to improve the solution that was produced in the construction phase. In this case, a local search procedure known as descent method was applied that works iteratively, successively replacing the current solution with a better solution in its neighborhood, the search ends when no better solution is found with respect to the function cost.
The success of a local search algorithm consists of the adequate choice of a neighborhood structure, the efficient neighborhood search technique and initial solution. The GRASP construction phase plays an important role in the last point as it produces good initial solutions for local search [14].
The neighborhood structure used in processing phase is 2-exchange (2-I). In practice, the flow matrix is taken, as well as the distance matrix and their elements are listed separately. The flows (matrix) are ordered from highest to lowest and the distances from least to greatest, both lists are restricted with a parameter 0< α < 1, they are multiplied generating a new list of elements of the form
This list is restricted with a parameter 0 < β < 1, with these operations you have a restricted list of candidates (RLC), from this list an element of the form is randomly selected
In the case of the second phase or improvement phase, taking as the initial solution the solution emanating from the first phase using a local search procedure, when this procedure is finished there will be a local optimal solution, which could also be a global optimal, algorithm 2 shows the pseudocode of the local search, where the input parameters are p that is the solution permutation produced in the construction phase and N(p) is the neighborhood of p.
5 SQAP Model
The SQAP is an application of the proposed QAP [7], the transformation is carried out by modeling a human trafficking system in a shopping center, the people who arrive at the shopping center are incorporated into a central corridor (circulation area flow of customers) also known as Steiner node where people walk in the direction of the place of their choice with a probability of going to place i, when leaving they go to place j with another probability of choice, the behavior of the traffic system it is modeled by means of: a waiting line with arrival rate, the departure rate with the parameters.
Before the previous steps, the objective is established, which is the allocation of services to the premises of the shopping center, in such a way that the layout of the businesses is planned in order to speed up traffic, avoiding crowds, defined in the following paragraph.
For the mathematical formulation in general of the SQAP as in [14] the following notation is considered:
|
customer transfer speed. |
|
distance between nodes (or locals) i to j. |
|
time of customer service that node i leaves to go to node j given by |
|
the probability that a customer leaves node i to node j. |
|
the arrival rate of a customer at node j. |
The Steiner node is considered to be a server with unlimited capacity, that is, as soon as a client enters the circulation of the system, there is a channel that provides the service, which is a function of the distance traveled in its transfer, it is that is, the waiting line behaves as if each client had its own server, therefore the Steiner node is a waiting line system [5].
In a system of waiting lines [16, 17] M / G / ∞ the average time spent in it is equal to the average time of service in the waiting line. In this case, the time spent in the system is the time that the client spends in the Steiner node, which is basically the time necessary for a client to move from node i to node j in the system. The time of stay for clients from node Steiner to node i is
where:
It is about finding the assignment of n services to n locals, that is, a permutation
6 Experiment and Results
To obtain the results, the instances obtained from QAPLIB [20], designed by [14, 26], of dimensions 12, 14, 15, 20, 21, 22, 24, 25 and 30 and 42[10], were taken, each instance is made up of three input parameters: dimension, distance matrix D and flow matrix F. The flow matrix was modified to obtain a transition matrix. The implementation proposed for GRASP in this study was with 500 fixed iterations, the parameters for the RLC are α = 0.2 and β = 0.3. It is worth mentioning that with the first phase of GRASP with two options an initial solution is generated, the second option is to generate multiple start-up solutions, subsequently, a post-processing phase with a search by neighborhoods of the type 2-exchange.
The program for carrying out the study was designed in JAVA programming language, likewise, the executions were processed on a TOSHIBA laptop computer with an i7 processor. In these tests, acceptable results were obtained, approximating the optimum as in the execution time.
The results of table 1 show that the GRASP implementation in Java of this work for QAP is efficient, since runs were carried out for the matrices proposed by Nugent, TE Vollmann and J. Ruml de Nug 20 to 30 available in [20].
Table 1 GRASP 2-I Neighborhood
| Instance | BKV | 2-exchange | Gap % |
| Nug 20 | 2570 | 2570 | 0.0 |
| Nug 22 | 3596 | 3596 | 0.0 |
| Nug 24 | 3488 | 3496 | 0.2 |
| Nug 25 | 3744 | 3748 | 0.1 |
| Nug 27 | 5234 | 5236 | 0.0 |
| Nug 28 | 5166 | 5178 | 0.2 |
| Nug 30 | 6124 | 6156 | 0.5 |
Column 2 shows the optimal values reported on the internet and the third column shows the results obtained, where the least favorable gap of the runs was less than 0.5%.
Table 2 shows the summary of the best results obtained in the four combinations of the execution of the proposed program, in the first column the initials DM means dimension of the matrix, C_PFP means combination of the first phase and post-processing phase of GRASP, MSG2-I is first phase multiple greedy solutions and second phase 2-exchange, G_2-I is first phase greedy algorithm with a single solution and second phase 2-exchange, BVF is the best value found by the combination, WVF is the worst value found by a combination, TCPU / milliseconds is the execution time of the best combination run.
Table 2 GRASP Execution Results
| n | C_PFP | BVF | WVF | TCPU |
| 12 | MSG2-I | 44.99 | 49.6 | 90 |
| 14 | G_2-I | 80.79 | 90.6 | 291 |
| 15 | MSG2-I | 91 | 101.2 | 191 |
| 20 | G_2-I | 194.99 | 215.99 | 1061 |
| 21 | G_2-I | 197.4 | 209 | 1348 |
| 22 | G_2-I | 300.4 | 310.2 | 1719 |
| 24 | G_2-I | 279.2 | 293.6 | 2252 |
| 25 | G_2-I | 308.4 | 340.59 | 2670 |
| 30 | G_2-I | 486 | 523.8 | 5556 |
| 42 | G_2-I | 182 | 182.07 | 20001 |
Table 3 shows the allocation permutations of each test instance, which indicate the allocation of stores to premises in a shopping center and the objective values are the amount of circulation in a central aisle.
Table 3 Solutions of each instance
| n | Permutation |
| 12 | 4,6,11,8,5,10,2,1,12,7,9,3 |
| 14 | 9,3,8,13,1,12,5,7,6,10,11,14,2,4 |
| 15 | 4,2,11,14,6,13,7,12,3,10,1,8,9,5,15 |
| 20 | 17,5,7,4,13,8,6,2,19,20,1,10,12,11,9,3,18,15,14,16 |
| 21 | 5,2,9,14,6,11,4,20,21,3,18,16,8,15,12,13,7,19,10,1,17 |
| 22 | 17,15,4,16,8,11,22,10,7,21,20,5,6,14,18,1,3,19,12,13,9,2 |
| 24 | 2,19,1,18,6,5,21,13,12,3,9,14,7,10,22,11,16,23,20,24,17,8,15,4 |
| 25 | 5,12,4,20,22,24,8,25,10,15,17,23,14,7,13,18,3,9,19,16,2,6,11,21,1 |
| 30 | 24,25,19,7,21,28,17,1,10,2,13,30,26,12,22,8,20,29,5,23,11,3,9,4,15,6,18,27,16,14 |
| 42 | 25,16,24,42,11,12,20,10,6,40,3,36,35,23,32,22,21,1,5,38,19,41,37,7,15,28,2,31,9,34,8,26,29,14,39,18,13,33,17,27,30,4 |
The program was also executed for a problem proposed by [7] that presents instances of size n = 12, whose optimal solution is given by the permutation 7,3,2,11,8,12,9,10,1,4.6,5 with 172 customers circulating down the aisle.
7 Further Work and Conclusions
Finding solutions for SQAP is not an easy task as it belongs to the NP-hard class. The objectives set out in this work were first achieved with the implementation of a metaheuristic that allows a flexible and efficient tool to find solutions [10].
Subsequently, design test instances to execute the robust algorithm that offers solutions in a reasonable computation time (see TCPU in the table) and with approximation solutions to the optimal values for the SQAP.
Finally, in this research, an application was made to model the traffic of people circulating in a shopping center with a central aisle.
As future work, it is expected to expand the computational experience to matrices of greater dimension such as the Skorin Kapov matrix [26] that have dimensions from 49 to 100 and to design another metaheuristic to carry out comparison experiments, in order to increase the tools that contribute in the solution of practical-real application problems of the NP-hard class.
