1 Introduction
Fuzzy Cognitive Maps (FCM) are fuzzy-graph structures for representing causal reasoning, analyze inference patterns and they acts as a nonlinear dynamical system [1]. Application areas on which the FCMs have demonstrated an exceptional performance include decision support, process control, pattern recognition, and data mining systems. They have been applied on various domains such as biomedicine, geographic information systems, and time-series analysis [2].
In education, the causality characteristic allows the FCMs to be adequate to represent the dependence between key concepts of some domain of the knowledge in question, allowing to detect the learning material that should be delivered, to some student, with respect to their knowledge level and personal needs [3, 4]. Experts with an interactive procedure of knowledge acquisition build FCM [5].
Intelligent Tutoring System (ITS) is a system capable to guide students along a particular domain of knowledge through the solving of tasks tailored to the needs of the student [6]. In turn, a cognitive tutor is a type of ITS with a long-time proven efficacy. Its efficacy is based on its capacity to provide individualized support for the learning of complex cognitive abilities through the practice of problem solving [7, 8].
According to Gonzalez [6], the key components of traditional ITS can be organized in different modules as a student model, domain model, tutor model and interface or communication module, which interact with the user. In this paper, the interest is focused on the domain module; it contains the representation of expert knowledge in areas related to evaluation processes, teaching and learning methodologies, so that FCM that can represent the knowledge of the experts in the teaching of algebra are proposed. Although this module is also responsible for the reasoning-knowledge base and problem solving mechanisms, are processes that are still being worked, so they are left for a next research report.
Likewise, in the development of tools for facilitating the teaching-learning process it is necessary to use as a basis pedagogical, theories related to cognitive processes. Theory of cognition was a theory that made claims about the organization and acquisition of complex cognitive skills [9]. One such theory is known as the Cognitive Load Theory (CLT), which is based on the assumption that the construction and automatization of cognitive schemas for learning are the main goals of teaching.
However, those objectives may be thwarted by the limited capacity of working memory. Due to this factor, the proper allocation of available cognitive resources is essential for the learning process [10]. If a student has to spend limited resources on activities not directly related to the construction of schemes and automatization, learning can be inhibited [11]. Such activities may be related to the fact that the student should understand concepts that require previous knowledge that he does not recall or that he never learned. Within this theory, several approaches are handled, being one of them “expertise reversal”, which is based on classifying students as “experts” and “novices”.
Several existing studies have proven that designs and techniques which are effective for persons with a low level of knowledge may lose efficacy, and even have a negative impact, on more competent students [12,13]. Therefore, these studies conclude that instructional designs should be handled according to the knowledge level of students. In other words, there should be an analysis of the students’ current knowledge as well as to what is desired that he/she learn, because, if concepts are related, based on its complexity level, the student should have a solid grip on concepts previous to new knowledge. That is why one of the main concepts that have revolutionized the inclusion of cognitive sciences in the development of didactic models is the conception of knowledge as an intern representation that is built and organized in internal structures known as mental schemes or models.
Mental schemes allow the knowledge of the different states that in turn allow the maturity of expertise and the behavioral differentiation of novices and experts during problem solving that imply the use of different strategies to arrive to the solution. In order to make implicit knowledge available to the learner, some structured task must be available to elicit the knowledge from the learner [14].
Concept or cognitive mapping, represents a possible tool for developing such a structured environment [15] whereby, they are an element to be considered during the development of software systems that use artificial intelligence techniques, such as intelligent learning systems and expert systems, among others [14].
Here lies the importance of the representation of the dependency between the key concepts in the knowledge domain to be learned, and of not only using a general representation of knowledge the way conceptual networks do, should be in a deeper way. They should give answers to questions such as: “If a student learns the concept A, which is her/his knowledge level of the depended domain concept B? ”, or “If the student's knowledge of concepts A, B and C improves, how is her/his knowledge of the depended concept D affected?”, or “If the student has misconceptions on the domain concept A, how is her/his knowledge level of the depended concepts B, C and D affected?”.
In other words, they must represent how the knowledge of a domain concept of the teaching material, may be affected by the knowledge of another domain concept [4].
Because of the above-mentioned reasons, two of the main activities within the domain module are the detection of the dependency between the key concepts of a given subject, and the detection of students’ expertise level in each of the key concepts. These two activities have the purpose of guaranteeing that the implemented educational designs are adequate for learning achievement.
These designs are teaching processes whose implementation is not easy without help from automatized tools such as intelligent tutoring systems. For this research, in particular we are focusing on systems for algebra teaching and differential calculus, through problems solving using fuzzy cognitive maps, for represent the mental schemas that model dependencies between key concepts of domain.
The paper is organized of next form, in section 2, a description of basic concepts is made. In section 3, the description of models used in the paper are showed. Finally, in the section 4, a description of results is explained.
2 Basic Concepts
2.1 Cognitive Maps as the Basis of FCM
Political scientist Robert Axelrod (1976) introduced cognitive maps in the 1970s for representing social scientific knowledge. Robert Axelrod was the first to use the term in reference to the content and structure of individuals’ minds, thereby shifting its applied meaning from referring to a map that is cognitive, to a map of cognition.
Using Axelrod’s definition, cognitive maps are visual representations of an individual’s ‘mental model’ constructs, and are therefore analogous to concept maps that represent a person’s structured knowledge or beliefs [1, 9, 16].
Cognitive mapping means knowledge projection, and a cognitive map is basically a dynamical associative network which consists of nodes and directed arcs such that the nodes represent information associated with domain knowledge and the directed arcs represent cause-effect relationships between each pair of nodes [9].
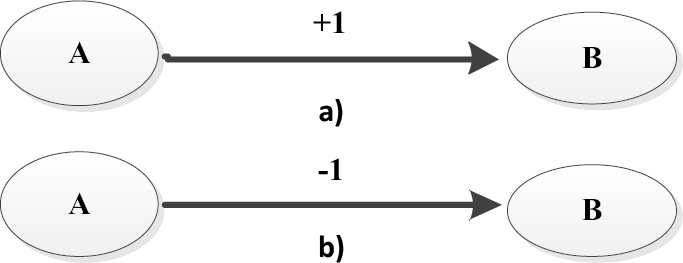
In the signed digraphs of Axelrod's cognitive maps, a positive edge from node A to node B means A causally increases B. A negative edge from A to B means A causally decreases B [1,15]. This type of systems could be seen as graphs that handle causal relations with values of -1 or 1 (see Fig 1), this means that the causal increment of one node over another is total, that is, it is considered that when the concept of origin node. A is fully increased and the weight associated to the edge connecting the source node to the destination node is 1 (Fig 1a), then it is interpreted as if the increase in the concept of the destination node B is also total. On the contrary, if the weight associated to the edge connecting the two nodes is -1 (Fig 1b), then when the value of the origin node A is fully increased, of destination node B is fully decreasing. However, this feature would not be including the full feature of fuzzy values, since in general, cognitive maps are too binding for knowledge base building and because causality is usually fuzzy. FCMs combine the strengths of cognitive maps with fuzzy logic.
By representing human knowledge in a form more representative of natural human language than traditional concept mapping techniques, FCMs ease knowledge engineering and increase knowledge-source concurrence. FCMs can also be modeled on computers, thus allowing for dynamic modeling of cognitive systems [13, 16].
The fuzzy indicates that FCMs are often comprised of concepts that can be represented as fuzzy sets and the causal relations between the concepts can be fuzzy implications, conditional probabilities, etc. In general, the edges Eij can take values in the fuzzy causal interval [−1, 1] allowing degrees of causality or weights to be represented [17, 13, 16]:
– Ejk > 0 indicates direct (positive) causality between concepts Cj and Ck. That is, the increase (decrease) in the value of Cj leads to the increase (decrease) on the value of Ck.
– Ejk < 0 indicates inverse (negative) causality between concepts Cj and Ck. That is, the increase (decrease) in the value of Cj leads to the decrease (increase) on the value of Ck.
– Ejk < 0 indicates inverse (negative) causality between concepts Cj and Ck. That is, the increase (decrease) in the value of Cj leads to the decrease (increase) on the value of Ck.
2.1.1. Modeling Fuzzy Cognitive Maps
For FCM reasoning process, a simple mathematical formulation is usually used. A model implication converges to a global stability, equilibrium in the state of the system. During the inference process, the sequence of patterns reveals the inference model. The simplicity of the FCM model consists in its mathematical representation and operation. So a FCM, which consists of n concepts, is represented mathematically by a n state vector A, which gathers the values of the n concepts, and by a n × n weighted matrix E. Each element Eij of the matrix indicates the value of the weight between concepts Ci and Cj. The value Ai of each concept Ci in a moment k + 1 is calculated by the sum of the previous value of Ai in a precedent moment t with the product of the value Aj of the cause node Cj in precedent moment k and the value of the cause-effect link eij. The mathematical representation of FCMs has the following form [1, 5, 17, 18]:
where f (·) is a threshold (activation) function. Sigmoid threshold function gives values of concepts in the range [0, 1] and its mathematical type is:
where m is a real positive number and x is the value
The transformation function is used to reduce unbounded weighted sum to a certain range, which hinders quantitative analysis, but allows for qualitative comparisons between concepts [5]. The main reason why this function is used is the same reason why the same function is used in artificial neural networks: goal is to describe human reasoning, and the sigmoid function provides a good approximate description of how similar processing in performed by the biological neurons in the brain [20].
FCM can be used to answer a “what-if” question based on an initial scenario that is represented by a vector S0 = {si}, for i = 1 . . .n, where si = 1 indicates that concept Ci holds completely in the initial state, and si = 0 indicates that Ci does not hold [18].
To characterize a real-life system, we must know its properties. Some of these properties come from measurements and, thus, are represented by real numbers. However, in many cases, a large amount of information comes from expert estimates[20]. The development of a FCM often occurs within a group context. The assumption is that combining incomplete, conflict opinions of different experts may cancel out the effect of oversight, ignorance and prejudice. An expert draws a FCM according to his experience. That is, each expert provides its individual FCM matrix, which is then synthesized into a group FCM matrix. The group matrix (EG) could be computed as [18]:
or
where
In a distributed system, a FCM is constructed for each subsystem. Then all FCM are combined in one augmented matrix E for the whole system. The unification of the distinct FCMs depends on the concepts of the segmental FCM. If there are no common concepts among different maps, the combined matrix E is constructed according to the equation (4) and the dimension of the matrix E is the total number of distinct concepts in all the FCMs [18]:
2.1.2. Fuzzy Cognitive Maps in Education
The areas and applications in which cognitive maps can be used are diverse. Even though the number of projects conducted in the field of education is still reduced, cognitive maps are a very useful tool, for they represent a kind of distributed intelligence since they can be seen as artifacts constructed to download complex tasks, structure activities, save mental work, and avoid mistakes.
When a graphical representation of a domain is created, cognitive maps release the user from having to keep such representation within his working memory, thus, freeing cognitive resources so they can be used for content interpretation and analysis [15], and for generating a structure that CLT denominates Cognitive Learning Schema. This schema will be useful for the tutor for the creation of the structure of the dependencies between the key knowledge concepts of the domain.
This is the main objective of this paper, where the domain is the comprehension of algebra topics for problem solving. The fuzzy part is made up from opinions from teachers with experience in the teaching of algebra, thus, transforming the cognitive graph into a fuzzy cognitive map and, at the same time, fulfilling the requisite of representing the knowledge of the experts.
However, when working with the causal dependency between the knowledge levels that a student possesses on a particular domain subject, a situation may arise in which the increase in the concept of any of the nodes of the fuzzy cognitive map may not be total, as represented in equations 1 and 2. Because of this, in these cases we should use a model that helps determine the causality between the nodes based on the dependency of the knowledge domain of the learning material. Chrisafiady et al. [4] define such model as a tuple (C, W, KL, f), where:
C= {C1,C2, .. . Cn} is the set of concepts of the domain knowledge.
W: (Ci,Cj) →wij is a connection matrix, where wij is a weight of the directed ard from Ci to Cj, which denotes that the knowledge level of the concept Ci affects that of concept Cj.
KL is a function that at each concept Ci associates the sequence of its activation degree. In other worlds, KLi(t) indicates the value of a concept’s knowledge level at the moment t.
f is a transformation function. For the definition of the transformation function, the following limitation has to be taken into account. The knowledge level of a domain concept is affected, each time, only by the knowledge level of the most recently read concept. The reason for this is the fact that the learner’s knowledge level is affected either by the new knowledge that s/he has obtained, or by the knowledge that s/he has forgotten, each time. Consequently, the KL value of a concept is affected only by the KL value of the most recently read concept, regarding the weight of the directed arc that connects them. Therefore, the transformation function for a FCM, which is used to represent the domain knowledge of the learning material, is defined as:
where pj is the percentage of the difference on the value of the knowledge level of the most recently read concept Cj, with pi = (KLj(t + 1)-KLj(t))*100/KLj(t). Also, the + is used in case of increase and the – is used in case of decrease.
2.1.3 Fuzzy Inference System
Fuzzy inference system (FIS) is a popular computing framework based on the concepts of fuzzy set theory, fuzzy if-then rules, and fuzzy reasoning. It has found successful applications in a wide variety of fields, such as automatic control, data classification, decision analysis, expert systems, time series prediction, robotics, and pattern recognition. The basic structure of a fuzzy inference system consists of three conceptual components: a rule base, which contains a selection of fuzzy rules; a database (or dictionary), which defines the memberships functions used in the fuzzy rules; and a reasoning mechanism, which performs the inference procedure upon the rules and given facts to derive a reasonable output or conclusion [21].
2.2 Tangible Interfaces
Others elements that we can include in a ITS are the tangible user interface (TUI), an “interface that is concerned with providing tangible representations of digital information and controls, allowing users to quite literally to grasp data with their hands”. The original motivation behind TUIs was indeed to connect the physical world with the digital one by using physical artifacts, therefore keeping the richness of physical interactions. This was novel and contrary to the main trend that focused on forcing the user into a virtual world [22]. Rather than make pixels melt into an interface, TUIs use physical forms that fit seamlessly into a user’s physical environment.
TUIs aim to take advantage of these haptic interaction skills, an approach significantly different from graphical user interfaces (GUIs). The key TUI idea remains: give physical form to digital information, letting it serve as the representation and controls for its digital counterparts. TUIs make digital information directly manipulatable with our hands and perceptible through our peripheral senses through its physical embodiment [23]. An example of a project that considers the management of tangible interfaces in virtual worlds is presented by Guerrero et all [24]. The main objective of this project was to do a study to assess whether the use of virtual worlds and tangible interfaces is beneficial for student learning when compared to more traditional forms of learning.
2.3 Model for Evaluation of Learning
Cognitive ability is closely related to learning acquisition and is the basis for developing instructional strategies, and their preferences are the basis for developing the type of mentoring [25].
For this reason, if we want to implement a strategy for the automatic detection of cognitive ability, we need an analytical model, which, through the management of instruments or rubrics, can in some way measure or assign a value to the cognitive ability. So that in this way a strategy can be implemented that can propose instructional designs according to these measurements.
Rongmei propose an analytical model, combined with fuzzy logic to categorize somehow students based on their cognitive ability and propose a model that is able to make the appropriate instructional design decision to the student, based on their progress. This model is the one that is being implemented in the part of the detection of the student´s cognitive ability in problem solve, of the proposal of this paper. The evaluation model can be expressed via a triple, such as formula 6 [25]:
where, U = (u1, u2, u3, u4, u5, u6), each element is respectively considered as the weight of one of the six evaluation indexes in this meta knowledge points, which is given by the experts. V= (v1, v2, v3, v4, v5), these elements respectively stand for five reviews: excellent, good, medium, passed and fail, which is based on both the results of cognitive ability synthetic evaluation and the test.
A is a matrix where each line has the following form:
where 𝑎𝑖 are values between 0 and 1 and are define as:
rij(1) is defined as the number of correct answers of the student in each of the cognitive abilities, rij(0) is the number of unanswered questions and rij(-1) is the number of incorrect answers in each of the cognitive skills.
Finally, M is defined as:
where:
and W defines the weight of each rubric, this is:
2.4 State of Art of Works on FCM in Education
In the educational context, models related to cognitive maps are used to generate tools related to the teaching - learning process, due to their ability to simulate and predict causal behaviors related to students' learning behavior. In this way, in [3], the authors propose some new dimensions of adaptively like automatic and dynamic detection of learning styles and provides personalization accordingly.
It has advantages in terms of precision and time spent. It is a literature-based approach, in which a personalized adaptive learner model (PALM) was constructed. Fuzzy cognitive maps and fuzzy inference system a soft computing techniques were introduced to implement PALM.
For its part in [26] a learning assessment system that uses multivariate analysis based on structural equation modeling and fuzzy cognitive maps as a tool. The main aim of the proposed system is to facilitate assessment of learning on interactive environments.
An adaptive and/or personalized tutoring system is an approach in which the domain knowledge should be represented in a more realistic way in order to allow the adaptive and/or personalized tutoring system to deliver the learning material to each individual learner dynamically taking into account her/his learning needs and her/his different learning pace. Peña and Sosa [27] use Rules-based Fuzzy cognitive maps so that through a decision-making approach they offer decision-making services to the sequencing module of an intelligent and adaptive web-based educational system (AIWBES).
Student-centered education aims at tailoring educational curricula, lectures and evaluation to satisfy students’ needs. In this way, an AIWBES is able to adapt intelligently interfaces, content, tests, support, and assessments according students’ likings and constraints with the purpose of enhancing their learning. In [4] the authors make use of fuzzy cognitive maps for representing graphically the information of domain concepts that constitute the learning material, as well as the knowledge representation approach has to allow the system to recognize either the domain concepts that are already partly or completely known for a learner, or the domain concepts that s/he has forgotten.
3 Description of the Models
The process that should be followed in the domain module is shown in figure 2 [28]. It is an iterative process consisting of three main processes for enhancing knowledge of topics of interest: 1) evaluation (“expertise reversal” effect); 2) cognitive map modeling; and, 3) assignment of different types of problems (“worked examples” effect).
3.1 Evaluation Process
For the evaluation process the fuzzy model, based on Bloom’s taxonomy, has already been published [29]; however, in this paper, the objective is focused to how obtain, automatically, input data for the fuzzy model. Is in this stage that we propose the use of networked tangible interfaces. Interfaces that, through game management, challenges or the physical representation of basic concepts of algebra and differential calculus, can obtain evidence of the student's progress in each subject. The first prototype, focused to evaluation of topic of algebra, is an interface that simulate a memorama game.
The prototype is connected to an electronic card, which stores game information, and by using electronic radio frequency cards; the association of algebra concepts can be simulated. In figure 3, the memorama prototype is showed. Another prototype for algebra issues is the one shown in figure 4, which helps evaluate the management of addition and subtraction with positive and negative numbers. In addition, for differential calculus issues, a prototype was implemented to help assess the student's abilities in identifying points on the Cartesian axes (figure 4).
The objective of this project is to have a model to evaluate automatically the student with the data that is stored in the prototypes of tangible interfaces. Likewise, prototypes can also be used to help students reinforce various concepts, both of algebra and differential calculus, in a more interactive, graphic and tangible way.
Currently we are working on the reproduction and improvement of prototypes, so that, with the interconnection of prototypes through a Wi-Fi module, a local network can be designed, in which the teacher's personal computer functions as a server. Therefore, it will be on the teacher's computer where the database of Figure 2 and the fuzzy models proposed as part of this research are stored.
3.2. Fuzzy Cognitive Maps for the Second Process
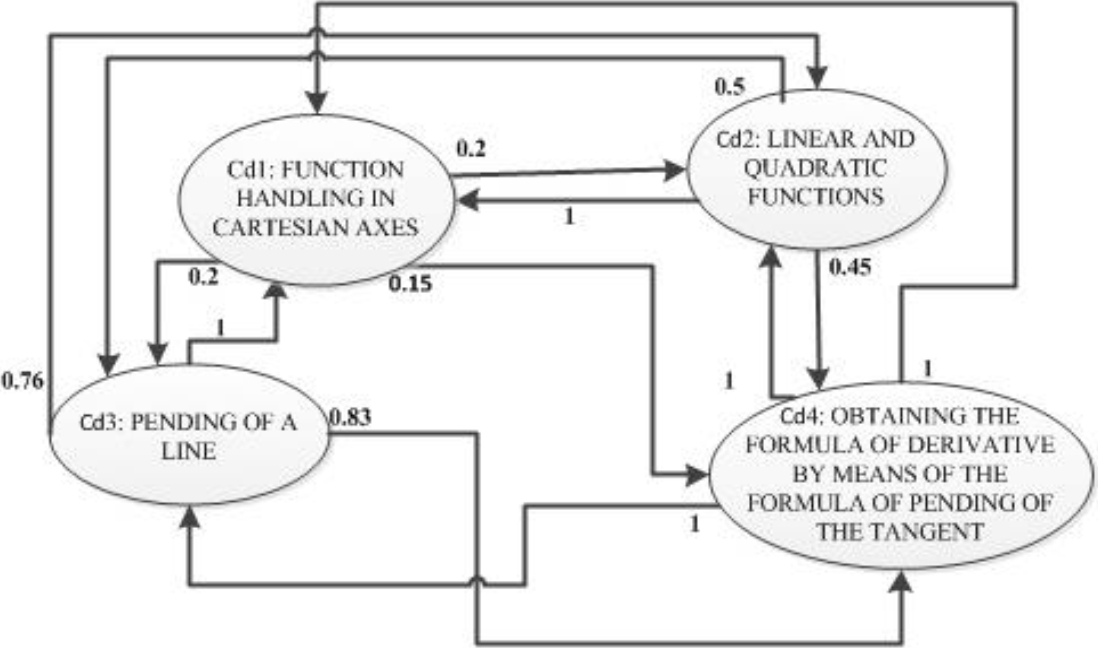
For the second process, modeling cognitive maps, two maps are proposed, one for the management of algebra issues and another for the management of differential calculus issues. For algebra, 5 topics are considered and for differential calculus, 4 topics are considered, which are shown in figures 6 and 7, as part of the fuzzy cognitive maps that are proposed, indicating the values of the edges, obtained from the opinion of teachers who they teach these subjects.
Formally, using the elements described in section 2.1.2 of this paper, the set C for the cognitive map of algebra, which we denote by Ca is defined as:
Ca = { Ca1:Identify algebraic language;
Ca2: Notation and classification of algebraic expressions;
Ca3: Algebraic representation of expressions in common language;
Ca4: Interpretation of algebraic expressions;
Ca5: Numerical evaluation of algebraic expressions}.
And for the cognitive map of differential calculus, which we denote by Cd is composed of:
Cd = {Cd1: function handling in Cartesian axes;
Cd2: Linear and quadratic functions;
Cd3: Pending of a line;
Cd4: Obtaining the formula of derivative by means of the formula of pending of the tangent}.
In this way, the matrix of weights for each cognitive map is defined as shown in Table 1 and 2 respectively. The number of rows of this matrix is equal to the number of columns, and it is equal to the number of the nodes (domain concepts) that are depicted to the FCM. The values of the directed arcs of the FCM are written into the cells of the matrix.
Table 1 W-matrix with knowledge dependencies among algebra topics
| Ca1 | Ca2 | Ca3 | Ca4 | Ca5 | |
| Ca1 | 0 | 0.8 | 0.3 | 0.7 | 0.36 |
| Ca2 | 0.93 | 0 | 0.4 | 0.5 | 0.25 |
| Ca3 | 0.61 | 0.6 | 0 | 0.5 | 0.31 |
| Ca4 | 0.55 | 0.29 | 0.51 | 0 | 0.4 |
| Ca5 | 0.31 | 0.24 | 0.3 | 0.4 | 0 |
Table 2 W-matrix with knowledge dependencies among differential calculus topics
| Cd1 | Cd2 | Cd3 | Cd4 | |
| Cd1 | 0 | 0.2 | 0.2 | 0.15 |
| Cd2 | 1 | 0 | 0.5 | 0.45 |
| Cd3 | 1 | 0.7 | 0 | 0.8 |
| Cd4 | 1 | 1 | 1 | 0 |
The matrix is completed row by row. The value of the “strength of impact” of the domain concept that corresponds to the matrix’s row i on the domain concept that corresponds to the matrix’s column j is written into the matrix's cell (i, j).
For example, the value of the “strength of impact” of the domain concept C1 on the domain concept C3, which are depicted in figure 6 or figure 7, is written in the corresponding matrix's cell (1, 3) (Table 1 or Table 2). The values of the matrix’s main diagonal are zero, since changes on the knowledge of a domain concept cannot affect the domain concept itself [4]. If a row of the matrix is read, then information about the domain concepts that are affected by the concepts which corresponds to the particular row, as well as about its “strength of impact” on them, will be extracted.
For example, if the second row of the matrix that is depicted in Table 1 is read, then information about the fact that changes on the knowledge level of the domain concept C2 affects at 93% the knowledge level of the domain concept C1 and at 40% the knowledge level of the domain concept C3, will be extracted. If a column of the matrix is read, then information about the domain concepts that affect the concept, which corresponds to the particular column, as well as about the “strength of impact” of them on it will be obtained.
According to the matrix that is depicted in Table 1, if the knowledge level of the domain concept Ca4 is increased, then the knowledge level of the domain concepts Ca1, Ca2, Ca3 and Ca5 will be increased also, but not in the same degree. According to the transformation function of the FCM (Equation 5, section 2.1.2) the following will be happened:
4 Discussion and Results
In general, the alterations of the knowledge level value of a concept causes change on the knowledge level value of its related concepts. Increase of the value of a concept causes increase of the value of its related concepts or decrease of the value of a concept causes decrease on the value of its related concepts. These alterations are conducted according to the transformation function of the FCM, and indicate the progress or no-progress of the learner.
For example, if the knowledge level of the domain concept “Identify algebraic language” for a learner is increased at x%, then her/ his knowledge level of all the related concepts. With this, it will be increased as it is presented in first column of Table 3, for x=55%, then the knowledge level of the related concepts will become as it is depicted in the others columns of Table 3. Here we assume that at the moment t (column 2), the student has a mastery of 68% for topic 2, 76% for topic 3, 42% for topic 4 and 35% for topic 5 of the map in Figure 6. Column 2 is the one that represents the initial vector S0, which is discussed in section 2.1.1 of this paper.
Table 3 Behavior of knowledge level of the depend concepts, from increase of 55 % of Ca1
| Domain concept | Increase Wij * pi | Knowledge Level (moment t) | Knowledge Level (moment t) |
| Ca2 | 0.8*0.55 | 0.68 | 0.97→97% |
| Ca3 | 0.3*0.55 | 0.76 | 0.88→88% |
| Ca4 | 0.7*0.55 | 0.42 | 0.58→58% |
| Ca5 | 0.36*0.55 | 0.35 | 0.41→41% |
In the same way, just as the increase in the level of knowledge can be modeled, the fuzzy cognitive map model can model the situation of a decrease, which, we would expect it not to happen, however, this can simulate the situation in which, a student forgets some concepts or processes. For example, Table 4 shows the case in which there is a decrease of the 30%, in the subject related to the “numerical evaluation of algebraic expressions” (Ca5).
5 Conclusions
The dependency between several algebra topics and differential calculus, as well as the relationship with problem solving, was modeled through a series of cognitive maps. It can be observed from the results shown that applying a variant of the original model proposed by Kosko a model that converges into an optimal vector using several incremental factors for each of the concepts related to the different subjects of algebra is obtained.
This allows us to simulate the dynamic behavior of the students’ learning process (“expertise reversal” effect), and to determine the kind of problems that should be offered to them as exercises to enhance their learning (“worked examples” effect). The latter is a process in which work is beginning.
The execution of the cognitive map convergence process has only been conducted to analyze the diverse combinations of input parameters.
However, the goal is to obtain real data from several students that may serve as an input vector for map modelling and, thus, obtain the parameters that will help in the training of the model that will assign the problems and topics in which the student should work in. All this, in order to achieve the final objective, which is to solve completely and autonomously every problem in each module, which will occur when the vectors associated to evaluation contain values that represent a total comprehension of every one of the concepts. This will be the vector, to which all fuzzy cognitive maps should converge. This way, the efficiency of the domain module could be evaluated.
For the FCM of Figure 7, an example with an increase of x= 68%, for the concept “Pending of a line” with the initial vector of the column 2, is showed in Table 5, and an example with a decrease of x= 46%, for the concept “Linear and quadratic functions” is showed in Table 6.











 text new page (beta)
text new page (beta)