1 Introduction
Entanglement of multipartite pure states has been object of many studies both theoretical and experimental [1,3]. The reason for the above is that multipartite entanglement is a basic ingredient for Quantum Information Protocols (QIP). Although certainly there have been advances in the study of multipartite entanglement [4,11], it is not yet understood the time evolution of the initial entanglement of a system of several qubits. In particular, it arises the question about the characteristics of the time evolution of the 3-tangle of a system of 3-qubit interacting mutually through a XY Hamiltonian.
As it has been pointed out in Ref. [4] the 3-tangle can be an important quantity for measuring the entanglement of a 3-qubit system. In the present paper we study the time evolution of the 3-tangle associated to a 3-qubit system in a pure state. In order to do the above we employ the 3-tangle introduced in Ref. [4] and also the quantum Heisenberg XY-Hamiltonian [12] for a system of 3-qubit.
Thus, given an initial 3-qubit state |ψ(t=0)⟩=c0(t=0)|000⟩+c1(t=0)|001⟩+c2(t=0)|010⟩+c3(t=0)|011⟩+c4(t=0)|100⟩+c5(t=0)|101⟩+c6(t=0)|110⟩+c7(t=0)|111⟩, the time evolution of such a state is given by the Heisenberg operator i.e. |ψ(t)⟩=e-iHt|ψ(t=0)⟩=c0(t)|000⟩+c1(t)|001⟩+c2(t)|010⟩+c3(t)|011⟩+c4(t)|100⟩+c5(t)|101⟩+c6(t)|110⟩+c7(t)|111⟩ where H is the XY-Hamiltonian of the 3-qubit system. In our approach, we derive an analytic expression for the Heisenberg operator e-iHt with which if the initial 3-tangle (𝒯(t = 0)) is known in terms of the initial coefficients {ci(t=0)} (i=0,1,…,7) then the final tangle 𝒯(t) will be known in terms of the final coefficients {ci(t)} (i=0,1,…,7), the value of J and the time t.
As a result we find noticeable harmonic-like time behavior for the 3-tangle. The later seemingly suggests that the entanglement of a 3-qubit system interacting through a XY Hamiltonian is a quantized quantity. The paper is organized as follows: in Section 2 we derive the formalism for a 3-qubit system interacting through a XY-Hamiltonian. In Section 3 we find an expression for the 3-tangle as a function of time. Finally, we conclude the work by giving a discussion of our results in a section of Conclusions.
2 3-qubits XY Hamiltonian
In order to facilitate our calculations it is employed the decimal notation, which is defined as follows:
Then, a general pure 3-qubits state can be defined in terms of a superposition of the above basis as follows:
where:
With the decimal notation it is possible to associate a matrix with a Hamiltonian operator. The respective associated matrix elements to the Hamiltonian operator H become:
The so called XY-Hamiltonian for n qubits is: [12]
where N = 2n, J is the coupling constant, and Sai is the a (a = x, y) component of the spin of the i - th qubit. In the present case we have n = 3 qubits (i.e. N = 8).
Let us observe that the states |0⟩ and |7⟩ are annihilated by the action of the operator H of Eq. (5), that is:
Furthermore, the action of the XY Hamiltonian H of Eq. (5) on the rest of the decimal states is:
Through the use of the Eqs. (4)-(7) and the orthonormality of the decimal basis, the construction of the matrix associated to H yields:
On the other hand, the time evolution operator can be expanded in powers of H as follows:
We observe that the several different powers of H of Eq. (8) behave peculiarly. For instance the quadratic power is:
In a similar way, for the other powers we obtain that:
ewhere I{2-7} has been defined in Eq. (11). In general for the n - th power we find that:
However, we can see that an=2bn-1 and bn=bn-1+an-1=bn-1+2bn-2, then the above equation can be expressed as:
We observe from the above equation that for n = 0, the second term will be equal to zero and that the first one is equal to 1. However, in this case, H0=I{2-7} and this is not the identity I8 as can be seen from Eq. (11). Such a problem can be solved as follows:
where:
From the above equation we find that the time evolution operator will always be linear on H, and the time evolution operator can be written as:
It is worth to observe that the last expression can be written in terms of exponentials with which the time evolution operator takes a simple form:
Let us note that according to Eqs. (9) and (10) the time evolution of the state |ψ(t=0)⟩ is given by:
It can be observed from the above equation that we can calculate the coefficients at any time {cj(t)}(j=0,1,…,7) if the initial coefficients {cj(t=0)}(j=0,1,…,7) are known and if it is also known the action of the time evolution operator on each of the decimal states, that is, U(t)|i⟩ for i = 0, ...,7. Through the use of Eqs. (6), (7), (11), (16), and (18) it is found that:
To substitute Eqs. (20)-(27) into Eq. (19), we find the coefficients at any time {cj(t)}(j=0,1,…,7) in terms of both the above exponentials and the initial coefficients {cj(t=0)}(j=0,1,…,7) where ∑7j=0|cj(t=0)|2=1.
3 3-tangle as a Measure of Multipartite Entanglement of a 3-qubit System
The measure of entanglement for a 3-qubit system can be is obtained through the 3-tangle which is defined as [4]
with:
where c i represents the coefficient of basic state |i⟩. Thus, by calculating the coefficients ci (i = 0, 1, ... , 7) as a function of time, in the way it was explained at the end of the above section, we shall be able of finding the 3-tangle of Eq. (28) as a function of time. That is to find T3(t)=4|d1(t)-2d2(t)+4d3(t)| providing the coefficients ci (t) are known. It is worth to observe from Eqs. (18) and (19) that the coefficients ci (t) (i = 0,1,..., 7) will depend on the initial coefficients cj (t = 0) (j = 0,1,7), the antiferromagnetic constant J and the time t. By the way, in the present work the initial coefficients cj (t=0) (∑7j=0|cj|2=1) are found in a random way with which the coefficients ci (t) (i = 0,1, ...,7) at time t will result a two variables function namely J and t.
Before of considering a general state we are focusing on the so called W and GHZ states which are defined as:
The respective initial 3-tangle for the GHZ-state is unit while for the W-state the initial 3-tangle is zero. Now, the W-state time evolution is only over the phase. Therefore the 3-tangle of the W-state does not change in time. Thus, the XY Hamiltonian keeps constant the entanglement of the W-state which is an important result. On the other hand, the GHZ-state also is not modified by the time evolution operator of Eq. (19) hence its associated 3-tangle keeps constant in time. We conclude that the XY Hamiltonian assures that the entanglement of the GHZ-state does not change in time.
Let us now consider an arbitrary initial 3-qubit state at t = 0 denoted by |ψ(t=0)⟩=c0(t=0)|000⟩+c1(t=0)|001⟩+c2(t=0)|010⟩+c3(t=0)|011⟩+c4(t=0)|100⟩+c5(t=0)|101⟩+c6(t=0)|110⟩+c7(t=0)|111⟩ where ∑7i=0|ci(t=0)|2=1. In order to evaluate the 3-tangle at time t from Eqs. (28)-(31), we employ eqs. (19)-(27) where the initial coefficients ci (t = 0) are found in a random way. We perform the above procedure in three different cases and calculate the respective 3-tangle in each one of the three different cases. In the Appendix we write the three different random initial 3-qubit states employed in the present work. In figure 6, we show the time evolution of the 3-tangle as a function of both j and t associated to each of the three different random initial 3-qubit states employed in the present work.
4 Relevance of Entanglement for Technological Applications
Quantum entanglement is essential not only for technological applications such as quantum computation [13], data base search algorithm [14] or quantum cryptography [15] and quantum secret sharing [16] but also for non-artificial systems. For instance for photosynthesis [17]-[18], navigational orientation of animals [19], the imbalance of matter and antimatter in the universe [20] and evolution itself [21].
5 Random Initial 3-qubit States
We write the three different random initial 3-qubit states that we have employed in the present work.
Such a states are the following:
We observe that all of the above three 3-qubit states are normalized to unit.
6 Conclusions
We have studied the behavior in time of the 3-tangle associated to a 3-qubit system interacting through the XY Hamiltonian given by Eqs. (5) and (8). The 3-tangle associated to the state |ψ(t)⟩=c0(t)|000⟩+c1(t)|001⟩+c2(t)|010⟩+c3(t)|011⟩+c4(t)|100⟩+c5(t)|101⟩+c6(t)|110⟩+c7(t)|111⟩ is given by Eqs. (28)-(31) where each one of the coefficients {ci(t)} (i=0,1,…,7) depend on the random initial coefficients {cj(t=0)} (j=0,1,…,7), J and the time t as it can be seen from Eqs. (18)-(27).
An important result obtained in the present work is that the entanglement of both the W-state and the GHZ-state keeps constant in time providing the three qubits interact through the XY Hamiltonian given by Eq. (5).
Such a result could have important experimental advantages whereas both the W-state and the GHZ-state can be used on solid basis for testing different QIP protocols.
In Figure we have plotted the 3-tangle of Eq. (28) as a function of both the time t and the antiferromagnetic factor J for three different random 3-qubit states. It is worth to point out that the 3-tangle shows a noticeable periodic behavior as it is appreciated from Figure being the respective period t=4π/J. Such a behavior in time is a consequence of the harmonic structure of the time evolution operator of Eq. (18).
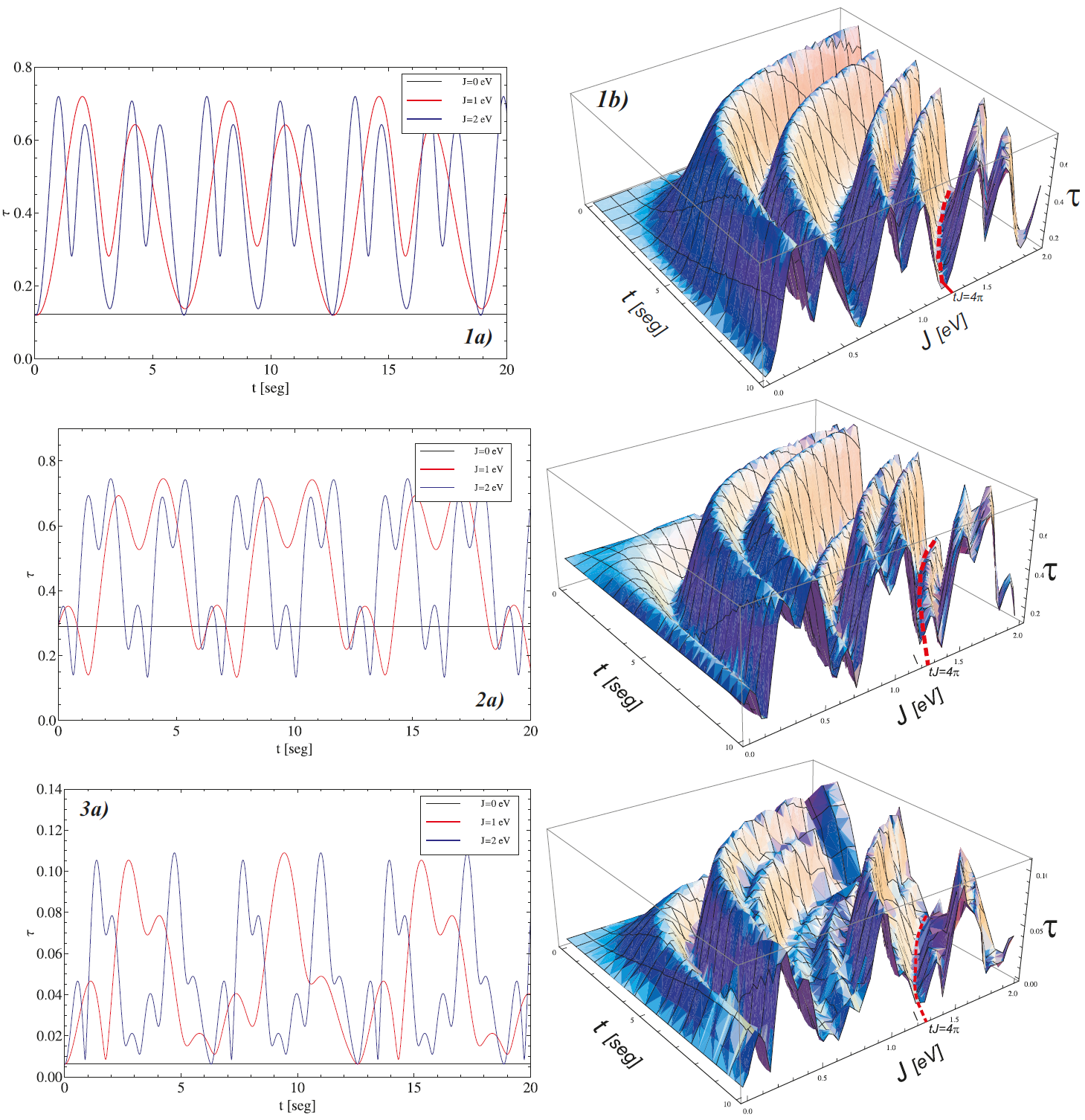
Fig. 1 The 3-tangle as a function of both the time t and the antiferromagnetic factor J for a three different states which their respective initial coefficients {ci(t=0)} are found in a random way. Eqs. (28)-(31) and (19)-(27) are used. Concerning to the label, the number represent the state while the letter expresses the kind of graphic
Our results invoke to the present experimental facilities to measure the 3-tangle for a system of 3-qubits by taking into account that for certain times the entanglement disappears and that for other values of both the time and the antiferromagnetic constant J such a quantity is maximal. The maximal values of the 3-tangle can be used for implementing Quantum Information Processing protocols where entanglement is a resource. Our results might indicate that the 3-tangle associated to a 3-qubit system resembles to a quantized physical quantity providing the three qubits interact through a XY Hamiltonian.











 text new page (beta)
text new page (beta)


