1 Introduction

One of the main nonlinear problem is the Fokas-Lenells (FL) equation

Where a ₁ and a ₂ are coefficients of group velocity dispersion, this model is the famous one which constructed as applications for current-fed string interacting with an external magnetic field. The perturbation terms η,γ,α, and on the right-hand side of Eq. (1) represent nonlinear dispersion, self-steepening effect, and, self-steepening effect, and inter-modal dispersion, respectively. There have been numerous approaches put forward by several authors to handle the approximate and exact solutions these nonlinear problems which are G’/G-expansion method, direct algebraic method, Sine-cosine method, tanh method, F-expansion method, and so on [^1-15]. To construct the analytical solutions of these equations for realized the dynamics structure is the mainly suitable way [^16-18]. The exact solution in explicit form of these models assist the confirmation of numerical researchers and also help in investigate the stability. The purpose of this work is to apply the G’/G-expansion method to solve the Fokas-Lenells (FL) equation . Such a study has not been considered before to our knowledge. This paper is outlined as follows: Section 2 gives a brief review of (G’/G)-expansion method. Section 3 contains the discussions. Finally, conclusion is given in Sec. 4. This paper is organized as follows: In Sec. 2, we describe the (G’/G)-expansion method while the application of the method has been presented in Sec. 3. The conclusions are drawn in Sec. 4.

2 Brief of the methodology

In this section, we briefly explain the application of (G’/G)-expansion to determine an exact solution for the partial differential equation. For given NLEEs of the form

Consider the wave transformation, u(x,t)=U(ξ), ξ=x-vt, Eq. (2) can be reduced to the following ODE:

Where U=U(ξ), and its total derivatives. the exact solution for the nonlinear ordinary differential equation can be written in the following:

where Gξ satisfies a second order linear ordinary differential equation:

And αn,n=0,1,2,…,m, are constants to be determined later.

Using the solutions of Eq. (5), we obtain

and from (4) and (5), we have

Therefore, here the prime denotes the derivative with respective to ξ.

3 Discussions

Let us use the transformation

where u(ξ) and ϕ(ξ) are real functions of the traveling coordinate ξ=x-vt. Here, v is the group velocity while Ω is the frequency of the wave oscillation.

Substituting the transformation (7) into Eq. (1), Thus we can easily get,

Equation (9) can be integrated after multiplying on u to induce

where the integration constant is taken to be zero. We set n = 1. Therefore, Eq. (9) reduces to

Thus we can easily obtain,

Now, substituting Eq. (12) into Eq. (8) leads to

where

According to Step 1, we put 5m = m + 2, hence m = 1. Therefore, we assume that the solution of Eq. (13) can be expressed by a polynomial in (G’/G) as follows:

Substituting Eq. (14) into Eq. (13) and collecting all terms with the same order of (G’/G) together , the left-hand side of Eq. (13) is conserved into a polynomial in (G’/G). Equating each coefficient of this polynomial to zero yields a set of simultaneous algebraic equations for λ, μ, ω, α0, α1, and α2. Solving the system of algebraic equations with the aid of Maple 16, we obtain the following three general results.

Case 1.

The first set of obtained results is

Where λ is an arbitrary constant. Therefore, substituting the above case in Eq. (17), we get solution of Eq. (1) for λ-4μ>0,

And for λ-4μ<0

The second set of obtained results is

we get solution of Eq. (1) for λ2-4μ>0

And for 4μ-λ<0

4 Conclusions

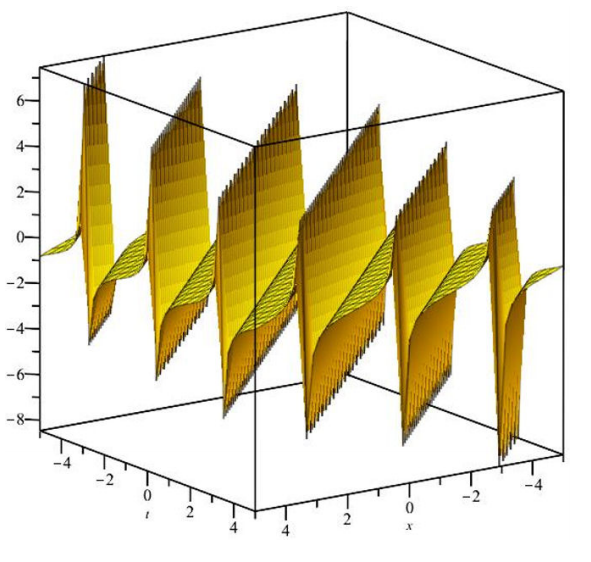
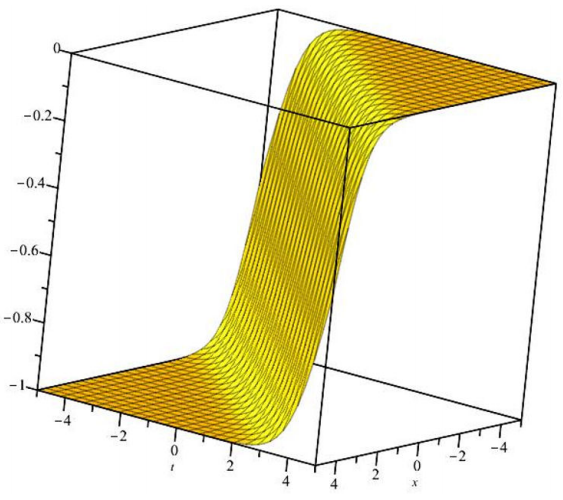
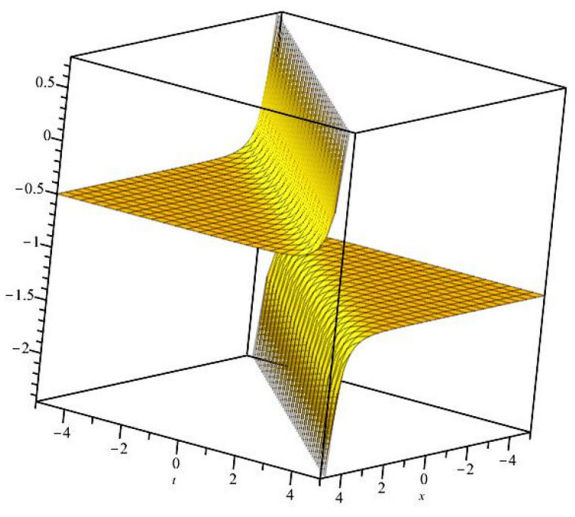
In this paper, we investigated the Fokas-Lenells equation via the G’/G- Expansion method. Using some wave transformations, the PDE system is turned into an ODE system. The solutions of the ODE system are assumed in the forms of the G’/G- Expansion method. In the same vein and parallel the FL has been applied to achieve other new visions to the soliton solutions of this model Figs, 1-3. The solutions will be considered for the new application areas of the generalized form of modified NSE. Consequently a positive forward future studies have been introduced for the given model. We also conclude that the effectively, powerful of the suggested method.

Figure 1 Graphical behavior for q ₁.  

Figure 2 Graphical behavior for q ₂. 

Figure 3 Graphical behavior for q ₃.