Research
Additive and multiplicative noises acting simultaneously on Ermakov-Ray-Reid systems
E. Cervantes-López1
P.B. Espinoza2
A. Gallegos2
H.C. Rosu3
1Instituto Nacional de Estadística y Geografía, Avenida Héroe de Nacozari Sur 2301, Fraccionamiento Jardines del Parque, 20276, Aguascalientes, México, e-mail: cer.ern@gmail.com
2Departamento de Ciencias Exactas y Tecnología, Centro Universitario de los Lagos, Universidad de Guadalajara, Enrique Díaz de León 1144, Col. Paseos de la Montana, Lagos de Moreno, Jalisco, México, e-mail: wolfgang@culagos.udg.mx; gallegos@culagos.udg.mx
3Instituto Potosino de Investigación Científica y Tecnológica, Camino a la presa San José 2055, Col. Lomas 4a Sección, 78216 San Luis Potosí, S.L.P., México, e-mail: hcr@ipicyt.edu.mx
Abstract
We investigate numerically the effect of additive and multiplicative noises on parametric oscillator systems of Ermakov-Ray-Reid type when both noises act simultaneously. We find that the main perturbation effects on the dynamical invariant of these systems are produced by the additive noise. Different from the separate action of the multiplicative noise when the dynamical invariant of these systems is robust, we also find a weak effect that can be attributed to the multiplicative noise.
Keywords: Noise; additive; multiplicative; Ermakov-Ray-Reid oscillator system; dynamical invariant
Resumen
Se investigan numéricamente los efectos de los ruidos aditivos y multiplicativos sobre los sistemas dinámicos de osciladores paramétricos de tipo Ermakov-Ray-Reid cuando los dos tipos de ruidos actúan de manera simultánea. La mayor parte de la perturbación del invariante proviene del ruido aditivo. A diferencia del caso cuando el ruido multiplicativo actúa por separado y el invariante dinámico presenta robustez, encontramos que en la acción simultánea de los dos ruidos hay también un efecto pequeño atribuible al ruido multiplicativo.
Palabras clave: Ruido; aditivo; multiplicativo; sistema oscilante de Ermakov-Ray-Reid; invariante dinámico
PACS: 05.40.Ca; 02.60.Cb; 02.70.-c
Ermakov oscillator systems are couples of second-order oscillator equations of the same operatorial structure of which one is linear and the other has an inverse cubic nonlinearity. The integrability link between the two equations has been known in Mathematics since the second half of the 19th century1,2 and a general nonlinear superposition connection between the solutions of the two equations has been found by Chini3 and rediscovered much later in a different format by Pinney 4. Another valuable feature of this type of systems of differential equations is the existence of an invariant quantity, usually known as the Lewis-Ermakov invariant, which is expressed in terms of the solutions of both equations5 . On the other hand, the Ermakov-Ray-Reid oscillator systems have been introduced in6 as an important generalization and proved to have extended applications in nonlinear optics7,8 , hydrodynamics9,10,11, magnetogasdynamics12 , and general relativity 13.
It is a fact of nature that oscillator systems, as any other dynamical systems, are affected by noises and to evaluate their effects is an important task14 . Our previous paper15 was the first one in the classical context to include the effects of the multiplicative noise upon Ermakov systems. For this case there are no big difficulties since the multiplicative noise can be treated as an intrinsic noise of the system associated to the frequency 14. In a second paper16 , we studied the effect of the additive noise, which proved to be more difficult than expected. Because of its additive feature, this common noise acts like a forcing term and then the Ermakov system should be extended with a second auxiliary nonlinear equation which is more complicated than the standard auxiliary equation. Moreover, we noticed that the noisy system is still tractable even if a forcing term of the Ermakov-Ray-Reid (ERR) type were included. However, the situations encountered both in natural environments and laboratory display the simultaneous presence of the two kinds of noise. Thus, in this work, we evaluate the cumulative noise effect on the generalized Ermakov invariant of forced ERR systems. This is done through the Euler-Maruyama numerical treatment used in our previous works which is recasted in the appropriate form for this more general case.
The starting point is the system of equations corresponding to the ERR system with an arbitrary forcing term f (t)17
ẍ+Ω2(t)x=ft+1x2ρg(ρ/x),
1
ρ̈+Ω2(t)ρ=kρ3 ,
2
ψ̈t+Ω2tψt=ρ2ḟt+3ρρ̇ft
+1x3ρgρ/xψ
3
where k is an arbitrary real constant and g (p / x) is an arbitrary function of argument p / x. Function p is the Ermakov auxiliary function while the ψ function is a second auxiliary function that should be introduced in the forced oscillator case. The dynamical invariant of this type of systems is given by 17
I=kx22ρ2+12ẋρ-ρ̇x2+ψ̇x-ψẋ+∫tψτfτdτ-ρ2xft+∫ρ/xg(τ)dτ.
4
By means of this extension to the forced case, it is possible to study the ERR systems with additive noise, taking the noise as the forcing term f (t) .16,18 On the other hand, the multiplicative noise can be included as a part of the parametric frequency Ω (t) 15. Following the same steps as in our previous works, the equations are solved numerically by means of the Euler-Maruyama method19,20,21 rewriting the system (1), (2), and (3) in the form
dYt=aYt(t)dt+bYt(t)dBat+cYt(t)dBmt,
5
where Bat and Bmt are the stochastic variables for the cases of additive and multiplicative noise, respectively. dYt stands for the following two-component vectors
dXt=[c]cdxdẋ, dρt=[c]cdρdρ̇, dψt=[c]cdψdψ̇
6
and the coefficients are given by
aXt=(x˙-Ω2x+gx2ρ),bXt=(0αa),cXt=(0αmx)
7
aρt=(ρ˙-Ω2ρ+kρ3),bρt=(00),cρt=(0αmρ)
8
aψt=(ψ˙ρ2f˙+gψx3ρ-Ω2ψ),bψt=(03αaρρ˙),cψt=(0αmψ),
9
where αa and αm are the amplitudes of the additive and multiplicative noises, respectively22 . It is worth mentioning that different stochastic variables are used for each type of noise since their origin resides in different physical effects: while the additive noise comes from external fluctuations with respect to the system, the multiplicative class are generic for the intrinsic fluctuations which can alter the frequency.
For the numerical calculations, we consider the same examples as in 15,16 with the same initial conditions x(0)=1,ẋ(0)=0,ρ(0)=1,ρ̇(0)=0, ψ(0)=1, ψ̇(0)=0. For the same reasons as presented in 16, the term ρ2ḟ has not been taken into account in the calculations.
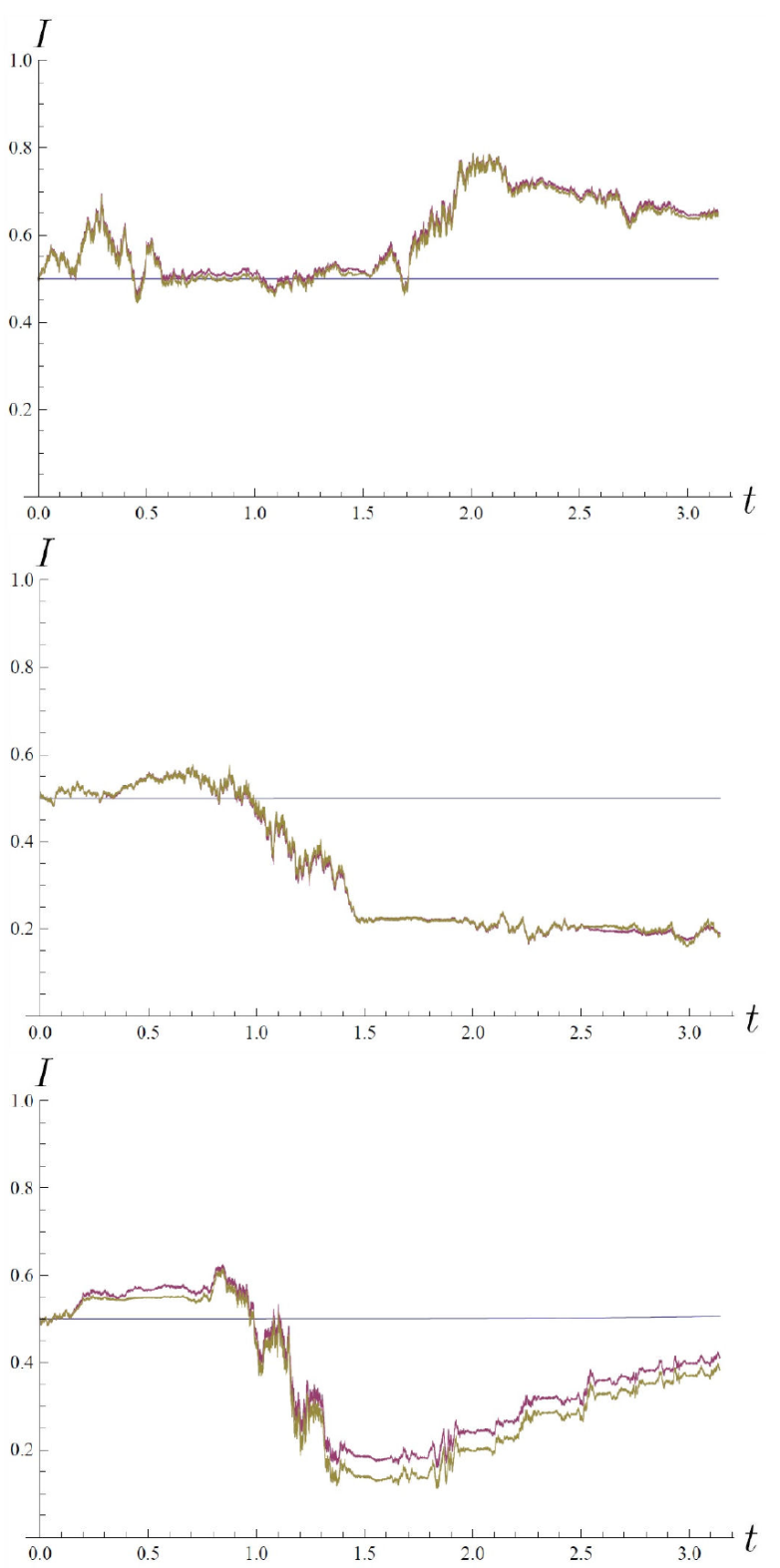
In Fig. 1, we display the dynamical invariants in the case g(ρ/x)=0 for the frequencies Ω(t)=2, Ω(t)=2sin(t), and Ω(t)=2t2. The curves in the blue color correspond to the noiseless cases, those in magenta are for αa=0.1 and zero multiplicative noise, and finally the green color corresponds to the amplitude of the additive noise αa=0.1 and multiplicative αm=0.1. In Fig. 2, the same cases are displayed for g(ρ/x)=k'ρ/x. The numerical calculations are performed by choosing k=k'=1. In Table I, we show the mean values and the standard deviations of the invariant for each of the cases.
Table I The dynamical invariants and their standard deviations for the cases considered here.

These results lead us to conclude that for ERR systems, the additive and multiplicative noises can be included in the usual way, i.e., placing the additive noise in the position of the forcing term and the multiplicative one as a perturbation of the frequency parameter of the system. The two noises should be treated as independent stochastic processes when they are included simultaneously in a parametric system. We notice that the dynamical invariant is sensitive to the additive noise as already found previously16 and robust to the inclusion of the multiplicative noise 15 when the two noise effects are considered separately. However, when they act simultaneously, we find out a weak effect of the multiplicative noise. Finally, we notice that ERR systems are slightly more robust when the external forcing term is of the Ray-Reid type, g(ρ/x)=ρ/x.
References
1. A. Steen, Overs. over d. K. Danske Vidensk. Selsk. Forh. (1874) 1.
[ Links ]
2. V.P. Ermakov, Univ. Izv. Kiev 20 (1880) 1.
[ Links ]
3. M. Chini, Atti Accad. Sci. Torino 33 (1898) 737.
[ Links ]
4. E. Pinney, Proc. Amer. Math. Soc. 1 (1950) 681.
[ Links ]
5. H.R. Lewis Jr., Phys. Rev. Lett. 18 (1967) 510.
[ Links ]
6. J. R. Ray and J. L. Reid, Phys. Lett. 71A (1979) 317.
[ Links ]
7. A.M. Goncharenko, Y.A. Logvin, A.M. Samson, P.S. Shapovalov, T.I. Surovets, Phys. Lett. A 160 (1991) 138.
[ Links ]
8. C. Rogers, B. Malomed, K.W. Chow, H.L. An, J. Phys. A: Math. Theor. 43 (2010) 455214.
[ Links ]
9. C. Rogers , W.K. Schief, J. Math. Anal. Appl. 198 (1996) 194.
[ Links ]
10. C. Rogers , H. An, Stud. Appl. Math. 125 (2010) 275.
[ Links ]
11. H. An , M.K. Kwong, H. Zhu, Stud. Appl. Math. 136 (2016) 139.
[ Links ]
12. C. Rogers , W.K. Schief, J. Math. Phys. 52 (2011) 0837101.
[ Links ]
13. W.K. Schief , C. Rogers , A.P. Bassom, J. Phys. A: Math. Gen. 29 (1996) 903.
[ Links ]
14. M. Gitterman, The Noisy Oscillator: The First Hundred Years, From Einstein Until Now, World Scientific, Singapore, (2005).
[ Links ]
15. E. Cervantes-López, P.B. Espinoza, A. Gallegos, H.C. Rosu, Physica A 401 (2014) 141.
[ Links ]
16. E. Cervantes-López , P.B. Espinoza , A. Gallegos , H.C. Rosu, Physica A 439 (2015) 44.
[ Links ]
17. J.R. Ray, J.L. Reid, Phys. Rev. A
26 (1982) 1042.
[ Links ]
18. M. Gitterman, The Noisy Oscillator: The First Hundred Years, From Einstein Until Now, World Scientific, Singapore, (2005), Chapter 8.
[ Links ]
19. B.K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, Springer-Verlag, Berlin, (2003).
[ Links ]
20. G.N. Milstein, M.V. Tretyakov, Stochastic Numerics for Mathematical Physics. Scientific Computation, Springer-Verlag, Berlin, (2004).
[ Links ]
21. P.E. Kloeden, E. Platen, Numerical Solution of Stochastic Differential Equations. Applications of Mathematics 23, Springer-Verlag, (1992).
[ Links ]
22. B.K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, Springer-Verlag, Berlin, (2003), p. 64.
[ Links ]











 text new page (beta)
text new page (beta)




