1. Introduction
Copper quaternary chalcogenide semiconductors are still of great interest due to their potential application as magnetooptic and thermoelectric materials, solar-cell absorbers, and photocatalysts for solar water splitting [1-4]. In general, this type of materials belongs to the families of normal semiconductor compounds with composition I2-II-IV-VI4, an equal number of cations and anions, and two good examples are Cu2ZnSnS4 and Cu2ZnSnSe4 which are naturally abundant and have shown conversion efficiencies as high as 10% [5]. These compounds adopt one of two well-defined sphalerite or wurtzite derivatives structures [6,7].
There are also defect quaternary compounds of the type I-III-IV-VI4, fewer cations than anions, which possess photoelectric and photo-luminescent properties that make them recent interesting from the point of view of their application as optoelectronic materials [8-10]. This family I-III-IV-VI4, better written as I-III-IV-⃞-VI4 were ⃞, denote the cationic vacancy, fulfill the rules of formation of adamantane compounds, and belongs to the defect semiconductor compound families [11]. However, for these materials, their crystalline structures have not been unambiguously established, due to the difficulty in the distribution of the cations in the available crystallographic positions (Wyckoff sites). Several members of this family have been structurally studied using photographic films taken at a Debye-Scherrer camera [12-14], founds unit cell parameters with tetragonal symmetry. However, in any case, were specified space group or structural details.
In these earlier studies, a defect chalcopyrite-type was assigned using a model where the disorderly cation I shared position with the vacancy while the cations III and IV share another atomic site. This model can be described as (Cu-⃞)(IIIIV)Se4 and was also used to describe the crystal structure of the quaternary compounds CuGaGeSe4 and CuInGeSe4 [15] in the tetragonal space group Iˉ42d where the cationic sub-lattice is disordered. Later, the crystal structure of the sulfide compound CuInSnS4 was described in the tetragonal space group Iˉ4 but also with a disordered distribution of their cations [16]. In this work, a detailed structural analysis for the compound CuAlGeSe4 was performed using X-ray powder diffraction, aiming to derive an ordered model that explains all the diffraction peaks in the powder pattern and to refine it employing the Rietveld method. Bond lengths derived from the refined results were used for the bond-valence sum (BVS) calculations [17,18], which allowed to verify the chemical sense of the structural model.
2. Experimental
The sample of CuAlGeSe4 was synthesized, through reaction in the solid-state of the constituent elements, Cu, Al, Ge, and Se, until reaching their fusion. The mixture was introduced into an evacuated quartz ampoule and brought to a horizontal two-zone furnace. The mixture was slowly heated up to 500◦C in 3 days. It was kept at this temperature for three more days. Then, it was heated at 110 0◦C and remained at this temperature for 2 hours. Then, the reacted mixture was annealed at 500◦C for a month. Finally, the sample was cooled to room temperature in about a day.
Chemical analysis was carried out with a Hitachi S-2500 scanning electron microscope (SEM) equipped with a Kevex EDX accessory. Three different regions of the ingot were scanned, and the average atomic percentages are Cu (17.52%), Al (15.34%), Ge (14.32%), and Se (52.82%). The error in the standardless analysis was around 5%. These values are in good agreement with the ideal composition 1:1:1:4.
A small quantity of the sample was ground mechanically in an agate mortar and pestle. The resulting fine powder was mounted on a flat zero-background holder covered with a thin layer of grease. The X-ray powder diffraction data were collected at room temperature, in θ/2θ reflection mode using a Siemens D5005 diffractometer equipped with an X-ray tube (CuK α1 radiation: λ = 1.54059 A; 40 kV, 30 mÅ) using a Ge < 111 > incident beam monochromator. Fix scatter of 0.1 mm, divergence slits of 1 mm, and a 0.1 mm receiving slit was used. The specimen was scanned in the 2θ range of 10-100◦, the scan step was 0.02◦, and the time of counting in every step was 46 s. The sample was rotated on its axis during exposure with a speed of 15 r.p.m. to avoid preferred orientation. Quartz was used as an external standard. The Bruker analytical software was used to establish the positions of the peaks.
3. Results and discussion
The indexing of the X-ray powder diffraction was performed using the program DICVOL [19]. The first 20 peak positions were used as input data. A solution with a tetragonal cell was given by the program. The following parameters were obtained: α = 5.5681(1) Å, c = 10.692(2) Å. The systematic absences study (hkl: h + k + l = 2n) indicated an I-type cell and the possible space groups Iˉ42d (No 122), Iˉ42m (No121), and Iˉ4(No 82).
To obtain the initial structural model before refining by the Rietveld method [20], several models were derived by permuting the cations in the available Wyckoff positions for the three space groups with Z= 2. Only in the space group Iˉ4 was it possible to accommodate all three cations and vacancy with a multiplicity of 2 in the atomic site maintaining an ordered distribution.
Therefore, different models were prepared in this space group alternating the position of the cations and vacancies in the available atomic sites: 2α(0,0,0), 2b(0,0,1/2), 2c(0,1/2,1/4), and 2d(0,1/2,3/4), with the anion Se in the atomic positions 8g (x,y,z) with x ≈ 1/4, y ≈ 1/4, z ≈ 1/8. The better refinement results were those where Cu1+ cation was placed in the Wyckoff site 2c: 0,1/2,1/4. Table I shows the six better models tested against the diffraction data employing the Rietveld method.
Table I Models employed in the Rietveld refinement of CuAlGeSe4.
| Model | (2c) | (2b) | (2d) | (2α) | (8g) | Rp | Rwp | χ2 |
| 0,1/2,1/4 | 0,0,1/2 | 0,1/2,3/4 | 0,0,0 | x,y,z | ||||
| Cu | Al | Ge | Se | 7.4 | 9.6 | 1.7 | ||
| Cu | Al | Ge | Se | 10.7 | 17.0 | 7.7 | ||
| Cu | Ge | Al | Se | 8.4 | 11.1 | 3.2 | ||
| Cu | Al | Ge | Se | 30.8 | 47.2 | 58.3 | ||
| Cu | Ge | Al | Se | 12.3 | 18.5 | 9.1 | ||
| Cu | Ge | Al | Se | 11.5 | 18.3 | 8.83 |
R exp=100[(N-P+C)/∑w(y2obs)] 1/2 R p=100∑|yobs-ycalc|/∑|yobs| χ2=[R2wp/R2exp] R wp=100[∑w|yobs-ycalc|2/∑w|yobs|2]1/2 N-P+C is the number of degrees of freedom.
The Rietveld refinement of the whole diffraction pattern was carried out using the FULLPROF program [21]. The atomic coordinates of the different models were used as the initial models for the Rietveld refinements. The angular dependence of the peak full width at half maximum (FWHM) was described by the Caglioti formula [22]. Peak shapes were described by the parameterized Thompson-CoxHastings pseudo-Voigt profile function [23]. The background variation was described by a polynomial with six coefficients. The thermal motion of the atoms was described by one overall isotropic temperature factor. From the figures of merit Rp, Rwp and χ 2, it was inferred that the best model is number 1. The results of the Rietveld refinement for model 1 are summarized in Table II. Figure 1 shows the/ observed, calculated, and difference profile for the final cycle of Rietveld refinement.
Table II Atomic coordinates, isotropic temperature factors and geometric parameters (Å,o ) for CuAlGeSe4.
| Space group Iˉ4 (No 82), Z = 2, α=5.5646(3) Å, c=10.682(2) Å, V=330.77(5) Å3 (Rexp=7.2%, RP=7.4%, Rwp=9.6%, χ2=1.7) | |||||||
| Atom | Ox. | Wyckoff | x | y | z | foc | B (Å2) |
| Cu | +1 | 2c | 0 | 1/2 | 1/4 | 1 | 0.4(4) |
| Al | +3 | 2b | 0 | 0 | 1/2 | 1 | 0.4(4) |
| Ge | +4 | 2d | 0 | 1/2 | 3/4 | 1 | 0.4(4) |
| 2a | 0 | 0 | 0 | 1 | 0.4(4) | ||
| Se | -2 | 8g | 0.2495(6) | 0.2423(4) | 0.1214(3) | 1 | 0.4(4) |
| Cu-Se | 2.421(3) | Al-Se(i) | 2.382(3) | Ge-Se(ii) | 2.365(3) | ||
Symmetry codes: (i)0.5-y, -0.5+x, 0.5-z; (ii)0.5-x, 0.5-y, 0.5+z.
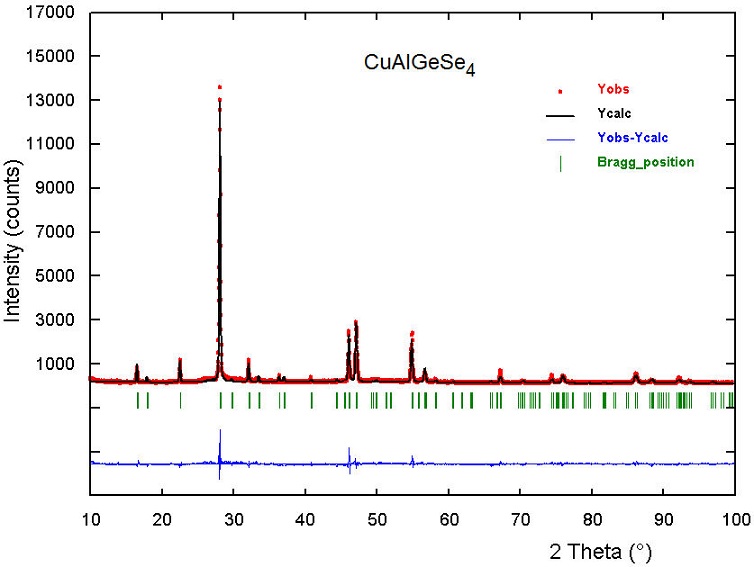
FIGURE 1 Rietveld refinement plot for CuAlGeSe4. The lower trace is the difference curve between observed and calculated patterns.
On the other hand, the entire pattern was reviewed utilizing the program NBS*AIDS [24] and the powder X-ray diffraction pattern was deposited in the ICDD-PDF with the code PDF-52-1024 [25].
CuAlGeSe4 is a defect adamantane-structure compound [11]. In this structure, each Se atom is coordinated by four cations [one Cu, one Al, one Ge, and one vacancy. In the same way, each cation is tetrahedrally bonded to four anions. The tetrahedra containing the Cu atoms [mean Se...Se distance 3.96(2) Å] are lightly smaller than those containing the Al atoms [means Se...Se distance 4.02(1) Å], and Ge atoms [mean Se...Se distance 4.24(1) A] respectively. Figure 2 shows the unit cell diagram of the CuAlGeSe4 structure where is possible to observe the tetrahedral environment around each of the atoms in the structure.
The Cu-Se distance [2.421(3) Å] is in good agreement with those observed in other adamantane structure compounds as for example the ternaries chalcogenide CuInSe2 (2.432 Å) [27], Cu2SiSe3 (2.423 Å average) [28], Cu2SnSeÅ (2.415 Å average) [29], and the quaternary compounds Cu2CdGeSe4 (2.410 Å) [30], Cu2CdSnSe4 (2.427 Å) [31], CuFeInSe3 [32], CuFe2InSe4 (2.456 Å) [33], and Cu2FeIn2Se5 (2.431 Å) [34]. The Al-Se distance [2.382(3)Å] compares well also with those observed in compounds as CdAl2Se4 (2.387 Å average) [35] and HgAl2Se4 (2.392 Å) [36]. The Ge-Se [2.375(3) A] is also in good agreement with similar distances in Cu2CdGeSe4 [30], and Cu2Cd 0.5 Mn 0.5 GeSe4 [37]. The structural model was confirmed by analysis of the interatomic distances using the Bond Valence Sum (BVS) formula founded on bond-strength examination [17,18]. These results are shown in Table III and are very close with the expected formal oxidation state of the cations Cu1+, Al3+, Ge4+, and the anion Se2−.
4. Conclusions
The crystal structure of the quaternary chalcogenide CuAlGeSe4 was established by an analysis of the cation distribution and the subsequent Rietveld refinement of the better model. This material crystallizes in the tetragonal space group Iˉ4 (No 82), unit cell parameters: α = 5.5646(3) Å, c = 10.682(2) A, V = 330.77(5) A3, with the following Wyckoff site atomic distribution: Cu in 2c (0,1/2,1/4), Al in 2b (0,0,1/), Ge in 2d (0,1/2,3/4), in 2α (0,0,0), and Se in 8g (x,y,z). This atomic distribution corresponds to an ordered fashion of all cations and anions in the crystal structure. The chemical structural model was confirmed by analysis of the interatomic distances using the Bond Valence Sum (BVS) formula.











 text new page (beta)
text new page (beta)



