Introduction
Concrete-faced hardfill dams are built mostly using granular materials, such as sand and gravel, obtained directly from the riverbed or its surroundings, or the same dam excavation by-products, artificially cemented together. It is common to have hardfills with 5 to 10% content of non-plastic fines. In recent years, the use of hardfill dams have increased worldwide due in part to its low cost and simplicity of construction. Generally, a typical hardfill dam is constructed using symmetrical trapezoidal sections. An impervious concrete-face is placed on the upstream slope. Hardfill dams heights range from 3 to 110 m approximately (Cai, Wu, Guo, & Ming, 2012; Mason, Hughes, & Molyneux 2012; Fujisawa & Sasaki, 2012; Guillemot & Lino, 2012). Traditionally, they have been classified as small to medium size dams (Cai et al., 2012; Guillemot & Lino, 2012). In particular, one of the highest hardfill dams reported in the literature is the Cindere dam, located in Turkey, which is 107 m high, and has a capacity of 84.3 million m3 (Guillemot & Lino, 2012; Batmaz, 2003). The trapezoidal shape helps minimizing stresses within the dam body and foundation as well as reducing oscillations during a seismic event (Xiong, Weng, & He, 2013). Some of the main advantages of hardfill dams are the quick and simple construction because of the strength demand on foundation is relatively less than that required in other types of dams such as gravity dams with typical sections, and also that the specifications of aggregates and cement are less stringent, which results in reduced production cost of hardfill. These facts, however, can lead to significant variations in as-built strengths and deformability parameters within the dam body (Batmaz & Gürdil, 2003).
Fragility curves relate the seismic intensity parameter to the probability of reaching or exceeding a given level of damage for each element at risk. The level of shaking can be quantified using numerous earthquake parameters, including peak ground acceleration (PGA), peak ground velocity (PGV), permanent ground deformation (PGD), spectral acceleration, spectral velocity or spectral displacement. To build these curves it is necessary to define some objective indicators that allow to estimate when the damage of a structure has passed from one level of damage to another. These levels are known as damage thresholds or damage degrees (e.g. minor, moderate, extensive and complete). Fragility functions are required elements for the assessment of vulnerability and risk (Argyroudis & Kaynia, 2015).
Fragility curves are essentially based on expert opinions and field observations. Nevertheless, one limitation when dealing with geotechnical problems, is the lack of well documented field data, with respect to damage indicators (e.g. permanent displacement, cracks and resisting exceedance force). The objective of this paper is to develop numerically-derived fragility curves for hardfill dams following the procedure proposed by (Argyroudis & Kaynia, 2015). Thus, commonly used geometry, structural parameters, rock foundation conditions, and a wide variety of ground motion characteristics are considered. This information partially fills the gap of information regarding the seismic response of this type of dams under medium to strong ground shaking.
Methodology
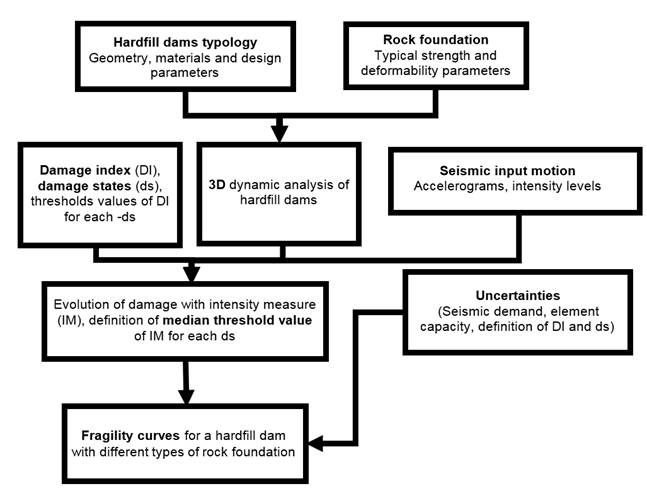
The procedure for developing numerically-derived fragility curves is described in Figure 1. First, the dam typology and hardfill and rock foundation mechanical parameters must be established, along with the material properties of the concrete face. Second, the damage states, ds, are stated, and the dynamic analysis of the hardfill-rock foundation dam is performed, considering a three-dimensional seismic environment. Third, the damage evolution is obtained for each intensity measure, MI, defining the value of the average threshold of MI for each, ds. Finally, fragility curves are derived for four damage states (i.e. minor, moderate, extensive and complete). These curves consider the uncertainty in seismic demand, capacity of each element, and the definition of the damage index and damage states. The response of the basin-rock foundation-dam coupled system is computed through a series of 3D finite difference dynamic analyses for an increasing level of seismic intensity using the software FLAC3D (Itasca Consulting Group, 2005). The geometry, material properties, and structure details are parameters, which describe the typology of the hardfill dam and its capacity to withstand seismic loads. The seismic loads are function of the seismic environment and basin-rock foundation-dam interaction. Three types of rock foundation were considered in the numerical study, to assess the effect of different deformability parameters on the vulnerability of a hardfill dam. Several ground motion were selected in terms of amplitude, frequency content and duration. Damage was quantified in terms of the shear stress acting on the dam under static and seismic loading, normalized by the shear strength (stresses capacity) on the dam.
Numerical model
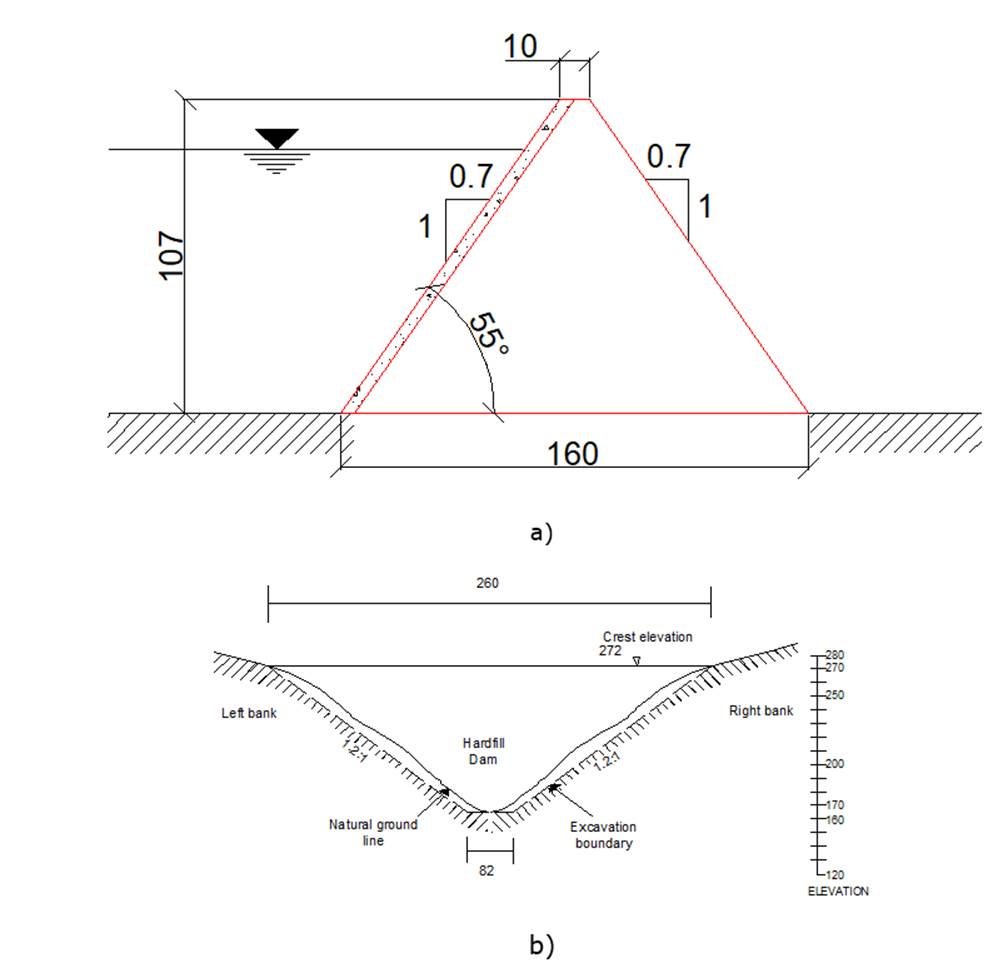
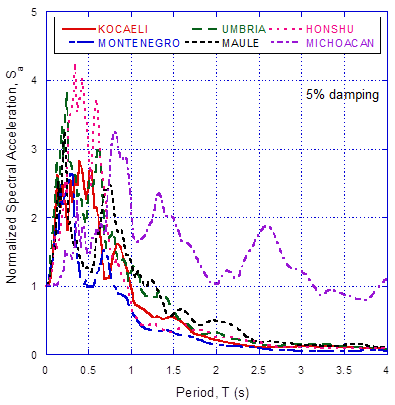
A numerical study was conducted in order to characterize the damage that a typical hardfill dam can exhibit for several seismic shaking scenarios varying from moderate to extreme ground shaking. It is worth mentioning that all the records used correspond to earthquakes measured at rock outcrops. A schematic representation of the dam geometry is presented in Figure 2. The dam is symmetrical, and 107 m high. The faces slopes are 0.7:1.0. The dam is considered founded on rock. Table 1 summarizes information regarding the earthquakes considered in the analyses, and Figure 3 shows the corresponding response spectra.
Table 1 Earthquakes considered in the analyses.
| Seismogenic Zone | Earthquake Name | Year | Moment magnitude, Mw | Epicentral distance, Ed (km) | PGA (g) | Duration (sec) |
|---|---|---|---|---|---|---|
| Normal | Montenegro (former Yugoslavia) | 1979 | 6.9 | 21 | 1.774 | 48 |
| Kocaeli (Gebze, Turkey) | 1999 | 7.4 | 47 | 0.218 | 32 | |
| Umbria Marche (Gubbio-Piana, Italy) | 1998 | 4.8 | 10 | 0.235 | 40 | |
| Subduction | Maule (Concepcion San Pedro, Chile) | 2010 | 8.8 | 109 | 0.605 | 120 |
| Honshu (Haga, Japan) | 2011 | 9.0 | 283 | 0.814 | 300 | |
| Michoacan (Tacubaya, Mexico) | 1985 | 8.1 | 265 | 0.032 | 170 |
Three sets of rock foundation properties were considered in the analyses, as compiled in Table 2. The concrete deformation parameters used in the analyses are summarized in Table 3. For a given project, it is necessary to perform both laboratory and field tests to characterize strength and deformability parameters of the hardfill for short and long-term conditions, to conduct a final dam reliability assessment. For the cases studied included herein, these properties were defined from a statistical analysis of the information available in the technical literature (Zou, Li, Xu, & Kong, 2011; Xiong, Young, & Peng, 2008) as summarized in Table 4.
Table 2 Properties of the rock foundation used for the analysis.
| Properties | Units | Type C1 | Type C2 | Type C3 |
|---|---|---|---|---|
| Young modulus | MPa | 4903 | 9806 | 15475 |
| Shear Modulus, G | MPa | 2114 | 4227.0 | 6670 |
| Volumetric weight γ | kN/m3 | 25 | 26 | 27 |
| Poisson ratio ν | 0.16 | 0.16 | 0.16 |
Table 3 Concrete properties used in the analyses.
| Properties | Units | Concrete |
|---|---|---|
| Young modulus, E | MPa | 28000 |
| Volumetric weight,γ | kN/m3 | 24 |
| Poisson ratio, ν | 0.20 |
Table 4 Typical hardfill properties reported in the technical literature.
| Cohesion, c (MPa) | Friction angle, φ (°) | Young modulus, E (MPa) | Cement content (kg/m3) | Curing time (days) | Confining stress (kPa) | Reference |
|---|---|---|---|---|---|---|
| 0.80 | 49 | 342 | 198 | 14 | 100 | Zou et al., 2011 |
| 0.42 | 46 | 341 | 132 | 14 | 100 | |
| 0.25 | 44 | 145 | 66 | 14 | 100 | |
| 0.24 | 49 | 594 | 60 | 28 | 200 | Sun & Yang, 2011 |
| 0.20 | 49 | 500 | 50 | 28 | 200 | |
| 0.12 | 49 | 450 | 40 | 28 | 200 | |
| 0.08 | 46 | 400 | 30 | 28 | 200 | |
| 0.08 | 42 | 250 | 20 | 28 | 200 | |
| 0.5 | 45 | 2,000 | 60 | 91 | --- | Xiong et al., 2008 |
| 0.8 | 45 | 4,000-11,586 | 70 | 180 | -- | Yanmaz & Sezgin, 2009 |
Short-term condition analyses
For short-term conditions, the hardfill cohesion, c, corresponds to the average of those values associated to a curing time of 14 days gathered from Zou, Li, Xu and Kong (Zou et al., 2011; Xiong et al., 2008) summarized in Table 4. Similarly, the internal friction angle, ϕ, corresponds to the lowest reported value.
Long-term conditions analyses
For the long-term conditions, the c and ф values associated to a hardfill curing time of 180 days were considered (Sun & Yang, 2011), which correspond to the mechanical properties of the hardfill parameters used in Cindere dam (Table 4). To take into account the evolution of hardfill properties with curing time a parabolic distribution was assumed. Figure 4 shows the evolution of the hardfill friction angle, cohesion and initial tangent elastic modulus considered in this study. The short and long term conditions parameters are summarized in Table 5.

Figure 4 Evolution a) Friction angle, b) Cohesion and c) Initial tangent elastic modulus of hardfill with curing time.
Tridimensional soil-structure interaction analyses
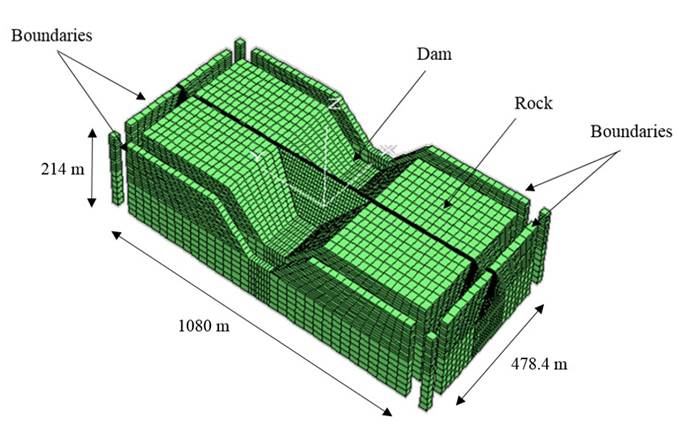
The seismic dam response analyses were carried out with a three-dimensional finite difference model, using the software FLAC3D (Itasca Consulting Group, 2005). The numerical model is depicted in Figure 5. The dam-foundation-embankment system was modelled with solid elements. This allows obtaining acceleration, velocity and displacements time histories simultaneously, along with strains and stresses. An elasto-plastic Mohr-Coulomb model was used to represent the stress-strain relationship for the hardfill. The rock and hardfill dynamic shear stiffness and damping variation as a function of shear strain during the seismic event was assumed negligible, considering the soundness of the rock foundation and that the hardfill should behave in its elastic range to avoid excessive and unacceptable cracking. The calculation is based on the explicit finite difference scheme, to solve the full equations of motion, using lumped grid point masses derived from the real density of surrounding zones. The added masses, required to account for hydrodynamic pressures in the numerical simulation, were obtained using the equation proposed by Chwang and Housner (1990). In the three-dimensional model a typical hardfill construction procedure was considered, which consists in a continued placement of hardfill layers with constant thickness (i.e. 1 m). The placement of one hardfill layer per day was simulated, considering the evolution of the hardfill properties with curing time explicitly in the model. The dam stages modelled were: 1) Sequential dam construction, 2) First reservoir filling, and 3) Seismic loading. The model depth is 214 m, the width is 480 m and the length 1080 m. The free field boundaries implemented in FLAC3D (Itasca Consulting Group, 2005) were used through the edges of the model. A flexible base was considered along the bottom of the model, to avoid boundary seismic wave reflection towards the dam-rock foundation system.
Fragility curves development
Hardfill dam numerically-derived fragility curves were obtained following the approach described in Figure 1. As previously described, the dam was assumed founded on rock. Three cases of rock foundation were considered to take into account the influence of their deformability parameters. The seismic loads are function of the surrounding rock, seismic environment and the basin-rock foundation-dam interaction. Several ground motions were selected based on amplitude, frequency content and duration. Finally, fragility curves were derived for different damage states (minor, moderate, extensive and complete) considering the primary sources of uncertainties.
Both normal and subduction earthquake type events were considered. A total of six ground motions recorded during these events were used in the analyses, exhibiting varying spectral acceleration amplitudes, frequency contents, significant durations and seismotectonic settings (Figure 3). The time histories are scaled to five intensity levels of PGA (i.e. 0.15, 0.30, 0.45, 0.60 and 0.75g) in order to perform the dynamic analyses of the basin-rock foundation-soil system for an increasing seismic excitation. Thus, a total of 90 cases were analyzed.
Damage index and damage states
A practice-oriented damage criterion for hardfill dams was proposed. Considering that there is currently a lack of relevant information on this subject, in this research the damage index, DI, is defined as the relationship between the shear stress acting on the dam, τact, considering both static and seismic loading conditions, normalized by the shear strength (stresses capacity), τcap, as follows:
where:
c is the hardfill cohesion, ϕ is the friction angle, the octahedral stress, σoct is defined as (σ1+σ2+σ3)3, and σ1, σ2, σ3 are the principal stresses.
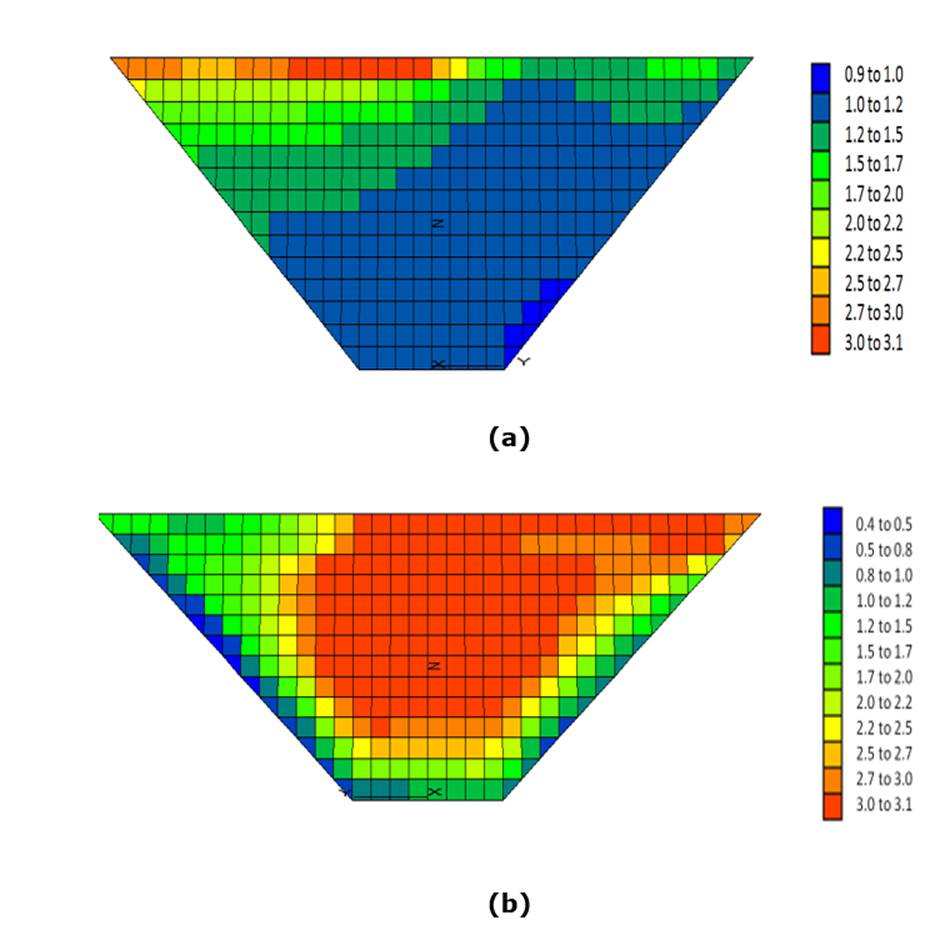
Four damage states were considered (i.e. minimum, moderate, extensive and complete, as summarizes in Table 6. In particular, Figure 6 shows the damage index contour through the dam body for the seismic subduction event of Maule, Chile, 2010, scaled to 0.75 g and considering the rock type 1. It can be observed that, in this case, the higher values of damage indices are concentrated in the downstream part of the dam.
Table 6 Definition of damage states for the hardfill dam.
| Damage states (dsi) | ds1 Minimum | ds2 Moderate | ds3 Extensive | ds4 Complete |
|---|---|---|---|---|
| Range of damage index | 0.5< DI (0.65 | 0.65< DI (0.8 | 0.8< DI (1.3 | 1.3>DI |
Derivation of fragility curves
Fragility functions describe the probability of reaching or exceeding a given damage state for a certain intensity measure. They are usually described by a lognormal probability distribution function, as follows:
where P f (•) is the probability of exceeding a particular damage state, ds, for a given seismic intensity level defined by the earthquake intensity measure, IM (e.g.; peak ground acceleration, PGA), Φ is the standard cumulative normal distribution, PGAffmi is the median threshold value of the earthquake intensity measure, required to cause the ith damage state and βtot is the total lognormal standard deviation. Therefore, the development of fragility curves requires the definition of two parameters, PGAffmi and βtot (Mayoral, Argyroudis, & Castañon, 2016). The lognormal standard deviation βtot, which describes the total variability associated with each fragility curve, is estimated considering the uncertainty in the definition of damage states (βds), the response and resistance (capacity) of the element (βC), and in the earthquake input motion (demand) (βd). Due to the lack of a rigorous estimation, βds is set equal to 0.4 following HAZUS (NIBS, 2004) approach for buildings, βC is considered equal to 0.4 based on engineering judgment (Argyroudis & Kaynia, 2015), while βd is estimated based on the variability in the hardfill response (DI) that have been calculated for the selected ground motions. The value of βtot is estimated as the root of the sum of the squares of the component dispersions. The median threshold value of the earthquake parameter, PGAffmi is obtained for each damage state based on the evolution of damage with increasing earthquake intensity.
Regression analysis
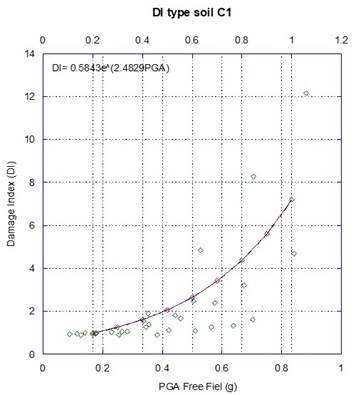
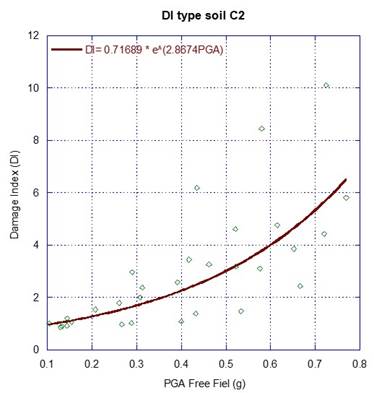
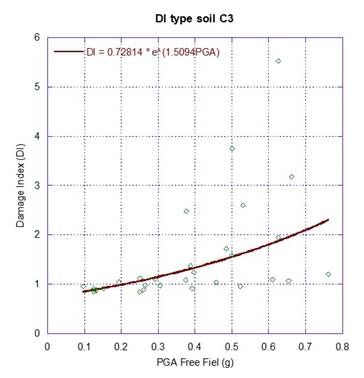
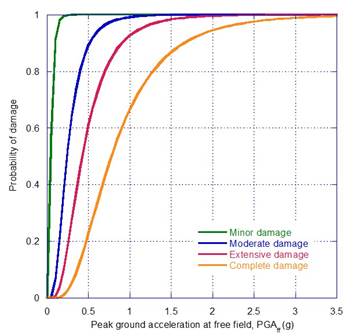
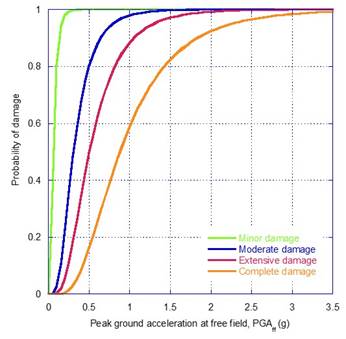
A regression analysis is performed, considering the damage index (DI) as the dependent variable, and the peak ground acceleration at free field, PGAff, as the independent variable, as it is illustrated in Figure 7, Figure 8 and Figure 9. The estimated parameters of the fragility curves are given in Table 7, and the corresponding fragility curves are illustrated in Figure 10, Figure 11 and Figure 12. The fragility curves were developed based on the peak ground acceleration determined at the free field, PGAff, for both subduction and normal-fault events scaled up to 0.75 g of PGAff. Evidently, the derived fragility curves can be applied for preliminary purposes only to cases where the dam foundation, foundation rock conditions and seismic environment are similar to those considered in the analyses. The development of this kind of functions, is a key step in seismic risk analyses to capture the most important seismic failure modes of the dam. Also, these are required to perform a proper seismic vulnerability assessment to foreseen the capacity of the system to withstand very large to extreme events, ensuring earthquake preparedness, and reducing life losses or post-earthquake distress.
Table 7 Parameters of the fragility curves.
| Case 1 | Case 2 | Case 3 | ||||
|---|---|---|---|---|---|---|
| Median threshold PGAffmi (g) |
βtot | Median threshold PGAffmi (g) |
βtot | Median threshold PGAffmi (g) |
βtot | |
| Minor | 0.47 | 0.569 | 0.76 | 0.614 | 1.10 | 0.572 |
| Moderate | 2.51 | 0.569 | 3.36 | 0.614 | 6.62 | 0.572 |
| Extensive | 5.01 | 0.569 | 6.54 | 0.614 | 13.39 | 0.572 |
| Complete | 8.24 | 0.569 | 10.63 | 0.614 | 22.10 | 0.572 |
Probability of failure
Uniform hazard spectra for four return periods (i.e. 125, 250, 475 and 2475 years) were obtained from the seismic hazard curves for both normal and subduction fault events. As it is well known, the uniform hazard spectra, UHS, is a representation of the relationship between the natural vibration period, T, and spectral acceleration, Sa, for a given exceedance probability associated with a return period. The uniform hazard spectra are shown in Figure 13a and Figure 13b for normal and subduction events respectively, which were used to obtain the peak ground accelerations (PGA). Then, with the PGA, and the numerically-derived fragility curves, the probability of reaching or exceeding the different states of damage (i.e. minor, moderate, extensive and complete) was computed, for each rock foundation type C1, C2 and C3, and the results are shown in Table 8. Overall, the numerically-derived fragility curves lead to high values of probability of damage. This appears to be over conservative, thus, more research is needed on the definition of the damage states to ensure more realistic results.
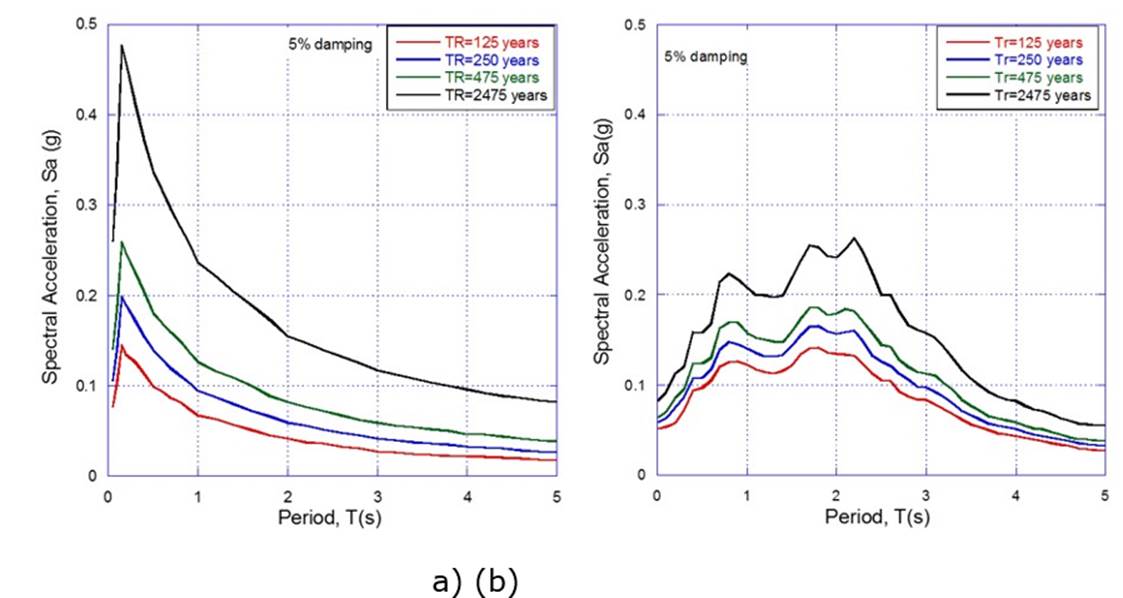
Figure 13 Uniform hazard spectra for Tr = 125, 250, 475 and 2475 years (a) normal and (b) subduction events.
Table 8 Probability of damage for C1, C2 and C3.
| Seismogenic Zone | Period Return | PGArock (g) | Probability of Damage (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | ||||||||||||
| Mi1 | Mo2 | E3 | C4 | Mi1 | Mo2 | E3 | C4 | Mi1 | Mo2 | E3 | C4 | |||
| Normal | 125 years | 0.12 | 0.391 | 0.159 | 0.056 | 0.008 | 0.939 | 0.525 | 0.194 | 0.025 | 0.714 | 0.164 | 0.028 | 0.001 |
| 250 years | 0.16 | 0.583 | 0.304 | 0.136 | 0.028 | 0.980 | 0.719 | 0.365 | 0.074 | 0.857 | 0.317 | 0.080 | 0.006 | |
| 475 years | 0.17 | 0.623 | 0.341 | 0.159 | 0.035 | 0.985 | 0.755 | 0.407 | 0.090 | 0.879 | 0.355 | 0.097 | 0.008 | |
| 2475 years | 0.22 | 0.773 | 0.511 | 0.287 | 0.084 | 0.996 | 0.876 | 0.590 | 0.191 | 0.948 | 0.531 | 0.197 | 0.026 | |
| Subduction | 125 years | 0.11 | 0.335 | 0.126 | 0.041 | 0.005 | 0.918 | 0.462 | 0.154 | 0.017 | 0.660 | 0.129 | 0.020 | 0.001 |
| 250 years | 0.12 | 0.391 | 0.159 | 0.056 | 0.008 | 0.939 | 0.525 | 0.194 | 0.025 | 0.714 | 0.164 | 0.028 | 0.001 | |
| 475 years | 0.14 | 0.493 | 0.230 | 0.092 | 0.016 | 0.966 | 0.633 | 0.279 | 0.045 | 0.798 | 0.239 | 0.051 | 0.003 | |
| 2475 years | 0.17 | 0.623 | 0.341 | 0.159 | 0.035 | 0.985 | 0.755 | 0.407 | 0.090 | 0.879 | 0.355 | 0.097 | 0.008 | |
Conclusions
A numerical approach is applied to construct fragility curves for hardfill dams under seismic loading. The response of the hardfill dam is evaluated based on 3D numerical models using the software FLAC3D. Seismic inputs with several frequency content and scaled to various levels of seismic intensity (PGAff) and typical rock profiles (Table 2) are considered. A practice-oriented damage criterion for hardfill dams was proposed. The damage index (DI) was established as the ratio between the shear stress acting, considering both static and seismic loading conditions, normalized by the shear strength. The fragility curves were derived as a function of the peak ground acceleration in the free field, considering the related uncertainties in the definition of damage states, the demand, and the capacity of the hardfill material used to build the dam. The applicability of the derived fragility curves has some constraints, which are related to the specific assumptions of the typology of the dam and selected parameters in the numerical models, so they become very specific for the cases studied, having to develop fragility curves for each condition and dam typology. Therefore, the provided fragility curves can be applied for preliminary purposes only, in those cases where the structure and rock conditions are similar to those considered in the analyses. Overall, the numerically-derived fragility curves lead to high values of probability of damage. This appears to be over conservative, and more research is needed on the definition of the damage states to ensure more realistic results.











 text new page (beta)
text new page (beta)