Introduction
One of the techniques to improve the management and control of a water distribution network consists in partitioning it into subsystems (called “districts” or “sectors”), delimited by closed boundary valves, and metering the amount of water that enters to them. This methodology, already implemented in many countries, helps to apply pressure management and other water loss control actions (WAA & WRC, 1985; Di Nardo & Di Natale, 2011) and to protect users from malicious attacks (Grayman, Murray, & Savic, 2009; Di Nardo, Di Natale, Guida, & Musmarra, 2012a).Two kinds of partitioning can be defined. In the first, and most known one, the water distribution network is divided in relatively small (usually between 500 and 3,000 properties) districts, each of them supplied by a limited number of pipes (preferably by a single pipe) in which flow meters are installed. The second one is related to multiple supply source networks. Most cities, especially medium and large cities, are fed by multiple water sources. This operation is not the outcome of a single process of planning and design, but the result of years of response to new continually rising demands and expansion of existing water distribution networks. Consequently, water sources in many cities are hydraulically interconnected by the city distribution network, without a clear delimitation of the zones supplied by each water source. It is very difficult to carry out water loss reduction and control programs in such conditions. The water quality of each water source varies, which makes the prediction and control of the water quality inside of a distribution network with interconnected water sources more difficult. The same is true for determining the extent of the danger, and time to recover, from a malicious attack or a spill accident of contaminants at water sources (Di Nardo, Di Natale, Santonastaso, Tzatchkov, & Alcocer-Yamanaka, 2012b). A good solution is to divide the water distribution network into isolated zones (sectors) in such a way that each zone is fed by its water source (or water sources). In order to distinguish this second kind of network partitioning ( (Di Nardo A. , Di Natale , Santonastaso, Tzatchkov, & Alcocer Yamanaka, 2012a); Di Nardo, et al., 2012a) introduced the term isolated District Meter Area (i-DMA). This way the first kind of network partitioning can be named DMA sectorization, as a synonym of “Division in DMAs” and the second one i-DMA sectorization. In multiple-source networks these two kinds of sectorization can be combined, i.e., if the application of the i-DMA sectorization produces large sectors, each of them can be further subdivided in DMAs.
The specialized literature presents very little work about the optimization of DMAs design. DMAs have traditionally been designed by a trial and error procedure where the pipes to be closed are proposed and a model of the distribution network is run repeatedly until a feasible solution, in terms of pressure and flow, is developed. Such a procedure lacks any rational basis; if a feasible solution is found, its quality in comparison with other feasible solutions is unknown. Because there are a vast number of possible network sectorizations even in small networks (Di Nardo & Di Natale, 2011), identifying the best one by trial-and-error procedures is difficult. Only recently some rational techniques have been published, based on multi-agent approach (Wooldridge, 2002), spectral clustering techniques (Ng, Jordan, & Weiss, 2001) and graph theory principles (Biggs, Lloyd, & Robin, 1986). With reference to the first technique, Izquierdo, Herrera, Montalvo and Pérez-García (2011) proposed an original procedure based on a multi-agent approach to define DMAs of a water supply network in which each agent is a consumption node with a number of associated variables (elevation and demand are most important) that obtains different scenarios. A spectral clustering technique was proposed by Herrera, Canu, Karatzoglou, Pérez-García, and Izquierdo (2010) to partition of a water supply network using dissimilarity matrices (transformed into weighted kernel matrices) obtained with graphical and vector information (pipes, demand nodes and water supply constraints. Giustolisi & and Savic (, 2010) described an algorithm for identifying the association between valves and isolated segments (or sectors), based on the use of topological matrices of a network whose topology was modified in order to account for the existence of the valve system and on the use of a genetic algorithm to minimize the number of isolation valves and the maximum total undeliverable demand. A heuristic Design Support Methodology (DSM) for partitioning a water supply system in DMAs, based on graph theory and analysis of the minimum energy paths computed from each reservoir to each network node, was later proposed by Di Nardo and Di Natale (, 2011. (Perelman & Ostfeld, 2011) presented a topological clustering algorithm for water distribution systems which, although not directed to DMA design, produces generic sectoring that may be useful in projects. More recently, Gomes, Sá Marques, and Sousa (, 2012a) published a two-step model methodology for designing DMAs. The first model divides the water distribution network into DMAs divides using graph theory concepts (Floyd-Warshall algorithm) and some user-defined criteria (network length, number of service connections, etc.), and the second uses a Simulated Annealing algorithm to identify the most appropriate number and location of metering stations, boundary valves and eventual network reinforcements. Very few works have addressed optimal i-DMAs sectorization design. (Di Nardo A. , Di Natale, Santonastaso , & Venticinque, 2011), and Di Nardo et al., 2012b proposed an approach for automatic i-DMAs design, based on graph theory coupled with a heuristic genetic algorithm optimization technique for the selection of pipes to close.
All published DMA and i-DMA design methods use flow directions in the network pipes. A water distribution network analysis model is run before applying them to obtain the flow distribution in the network, and it is assumed (implicitly) that the same flow distribution will remain after the sectorization. In graph theory terms, they work on directed graphs. But after closing the pipes that are needed to achieve the sectorization, the flow distribution in the network invariably changes and the premises on which the sectorization was obtained may be not valid. In their conference paper (Tzatchkov and Alcocer-Yamanaka (, 2012) defined several possible i-DMAs sectorization-specific graph partitioning criteria for undirected graphs, proposed an algorithm based on them, and applied it to a study case of a real medium city water distribution network. In this paper, the proposed procedure is extended to include a new graph theory based DMA sectorization design that can be applied in each i-DMA after the i-DMAs sectorization, or in single-source water distribution networks.
Methods
Known algorithms for graph partitioning
A water distribution network can be mapped, in a natural way, onto a graph whose edges are network pipes and whose nodes are pipe junctions or consumption points. Then, the design of its sectorization can be considered as a graph partitioning problem, for which, in principle, a wealth of techniques has been developed. There exist, however, important limitations when known graph partitioning techniques are to be applied to water distribution networks. In this paper such limitations are discussed and new water-distribution-network-sectorization-specific algorithms are proposed.
Graph partitioning techniques are commonly applied in distributed computing (Schloegel, et al., 2000). Large-scale numerical simulations on parallel computers, such as those based on finite element methods, require the distribution of the finite element mesh among the processors. This distribution must be done so that: 1) the number of elements assigned to each processor is the same, in order to balance the workload; 2) the number of adjacent elements assigned to different processors is minimized to reduce the communication overhead. Software packages that execute such partitioning algorithms are publicly available, e.g. CHACO, METIS, PARMETIS, PARTY, SCOTCH, JOSTLE and S-SHARP, as cited by (Fjällström, 1998) and Schloegel et al. (2000). Up to the knowledge of the authors of this paper, only two attempts to apply graph-partitioning techniques to water distribution network sectorization have been published so far (Sempewo, Pathirana, & Vairavamoorthy, 2008; Di Nardo et al. 2011). Both of them use a publicly available graph partitioning package (METIS). In those papers, the main objective of equally distributing workloads among the processors in parallel computing in METIS is likened to that of creation of zones of a water distribution system with equal water demand, and the objective of minimizing inter-processor communication to minimizing the number of pipe-cut or the number of boundary valves between the zones. Unfortunately the objectives of sectorization projects are different, as described below, therefore those partitioning techniques can have only limited application for real projects.
Sectorization-specific partitioning criteria
A natural condition for a good sectorization in a multi-source water distribution network is that every consumption node should be supplied by the water source closest to it. This way one possible criterion can be the minimization of the distances between a source node and each of the nodes it supplies. This criterion can be expanded to take into account the amount of water supplied, minimizing the product of the flow rate supplied to each node by the distance from the source to the node. Another similar criterion can be minimizing the cost of supplying the water, involving pipe diameters (and thus their cost) along the flow path from the source node to each consumption node. In all of these cases the flow rate in the pipes is not needed and the graph representing the water distribution network is handled as an undirected graph. After obtaining the proposed sectorization a pressure and flow analysis should be carried out, using a water distribution network analysis software, such as WDNETetXL ( Giustolisi, Savic, Berardi, & Laucelli, 2011) in order to revise its hydraulic feasibility.
Gomes, Sousa and Marques (2012b) used the ‘path length’ corresponding to the accumulated value of a weight η w associated with each pipe, given by the ratio of the flow Q to the pipe diameter D:
where δ and φ are the coefficients of the hydraulic resistance law equation. Another criterion, important for the control of water quality in large networks, can be minimizing the time water travels in network pipes before being supplied. Finally, a more refined measure for an optimum sectorization is the energy dissipated in the network P D , as proposed by (Di Nardo & Di Natale, 2011) given by:
where Q j and ΔH j are flow and head loss of each network pipe, m is the number of pipes in the network, and γ is the specific weight of water. In the last three cases the graph representing the water distribution network is handled as a directed graph and the flow rates and head loss in each pipe are needed, hence, the pressure and flow analysis needs to be obtained before analyzing the sectorization options.
All of these optimization criteria, combined with graph theory, can be used in the implementation of the i-DMA sectorization algorithm proposed in this paper, as explained below. Additionally, the capacity of the sources may be considered as restricted or non-restricted.
The proposed algorithm for i-DMA sectorization
Since water distribution networks may contain closed loops of pipes, water from a given source normally can arrive to a given consumption network node by more than one flow path. The first step in the proposed i-DMA sectorization algorithm is to find the shortest paths from each water source to each network node. What is needed, in fact, are not the shortest paths themselves but the distance traveled along them, where the term distance depends on the criterion of optimality applied as explained in the previous section. It can be the real distance (the sum of the length of the pipes) along the path, if the objective of the sectorization is to supply to the nearest nodes, for each water source, or the product of the consumption rate at the node and that distance, if the objective is to minimize this form of the cost of supply, or the dissipated energy expressed by Eq (1), and so on.
Several shortest path resolution algorithms can be found in the literature (Skiena, 1990); in this paper the Dijkstra algorithm has been chosen (Dijkstra, 1959)(Dijkstra, 1959). It allows to computing distances along the shortest paths without storing those paths, and can be applied to directed and undirected graphs (a directed graph is to be used if the dissipated energy (Eq (1)) is considered). The result of applying the Dijkstra algorithm in this case can be synthetized as a two dimensional matrix. Each row in this matrix represents a network node and each column a water supply source, so that its content is the distance from each source to each network node. Now, from that matrix for each network node the source with the shortest path distance is found and the node is assigned to be supplied exclusively by that source. This way the set of network nodes is divided into several non-overlapping subsets of nodes. The number of these subsets equals the number of supply sources and each of the nodes in the subset is supplied by one source.
If source capacities are restricted, then the nodes in each subset are sorted in ascending order according to their distance to the corresponding source and their water demand is accumulated in the same order. After that for each source the first nodes in the list whose cumulative water demand is not greater than the source capacity are assigned to that source, and the rest of the nodes in the subset are marked to be assigned to other water sources.
The last step of the algorithm is to find the set of edges (network pipes) that are to be closed in order to achieve that form of supply. These are the edges whose two nodes belong to different node subsets. In graph theory terms this set is named edge separator ( Diks, Djidjev, Sýkora, & Vrt'o, 1993).
The proposed algorithm for DMA sectorization partitioning
The problem is formulated as to find the network pipes to be closed that would divide the water distribution network in DMAs in such a way that each DMA is supplied preferably by one pipe (in order to minimize the number of water meters) and that the maximum size of each DMA is limited to a given number of service connections inside it. The following background terms from graph theory are used in the algorithm: If it is possible to establish a path from any vertex to any other vertex of a graph, the graph is said to be connected; otherwise, the graph is disconnected. The distance between two vertices u and v in a graph is the length of a shortest path between them. A tree is a connected acyclic simple graph. A tree structure is a way of representing the hierarchical nature of a structure in a graphical form. Every finite tree structure has a member that has no superior. This member is called the "root" or root node. The root is the starting node. The lines connecting elements in the tree are called branches, the elements themselves are called vertexes or nodes. A node's parent is a node one step higher in the hierarchy (i.e. closer to the root node) and lying on the same branch. A node that is connected to all lower-level nodes is called an ancestor. The connected lower-level nodes are descendants of the ancestor node. A child of a vertex v is a vertex of which v is the parent. Nodes without children are called leaf nodes, or leaves. In a tree structure there is one and only one path from any point to any other point. The degree, of a vertex v in a graph is the number of edges incident to v, with loops being counted twice. A vertex of degree 1 is a leaf, or pendant vertex. An edge incident to a leaf is a leaf edge, or pendant edge. A pendant subgraph is a subgraph that is connected to the graph by a single edge.
Breadth-first search (BFS) is a strategy for searching in a graph limited to essentially two operations: (a) visit and inspect a node of a graph; (b) gain access to visit the nodes that neighbor the currently visited node. The BFS begins at the root node and inspects all the neighboring nodes. Then for each of those neighbor nodes in turn, it inspects their neighbor nodes which were unvisited, and so on. A First-In-First-Out (FIFO) queue is employed to maintain the wavefront: v is in the queue if and only if wave has hit v but has not come out of v yet.
Based on these definitions, the proposed DMA sectorization algorithm is applicable to single-source networks. If the network is supplied by multiple water sources, the i-DMA sectorization algorithm presented in the previous section of this paper is used to divide it in several single-source subnetworks, and after that the DMA sectorization algorithm is applied to each of them. The algorithm starts with constructing a breadth-first tree of the network, rooted in the water source node s, by applying a modified breadth-first search traverse. At the beginning of the traverse it contains only the root node. Wherever a new node v is discovered in the course of scanning the adjacency list of an already discovered nodes u, the node v and the edge (pipe) (u,v) are added to the tree. The node u is a ancestor or parent of v in the tree. Since a node is discovered at most once, it has at most one parent. Ancestor or descendant relationship in this tree are defined relative to the root s as usual; if u is on a path in the tree from root s to vertex v, then u is an ancestor of v and v is a descendant of u. The path from s to any node in the breadth-first tree is the shortest path in terms of the number of edges. After obtaining the tree, the edges of the original graph are partitioned into tree edges and nontree edges. The tree edges are the edges that belong to the tree. The nontree edges are the edges that belong to the original graph, but do not belong to the tree.
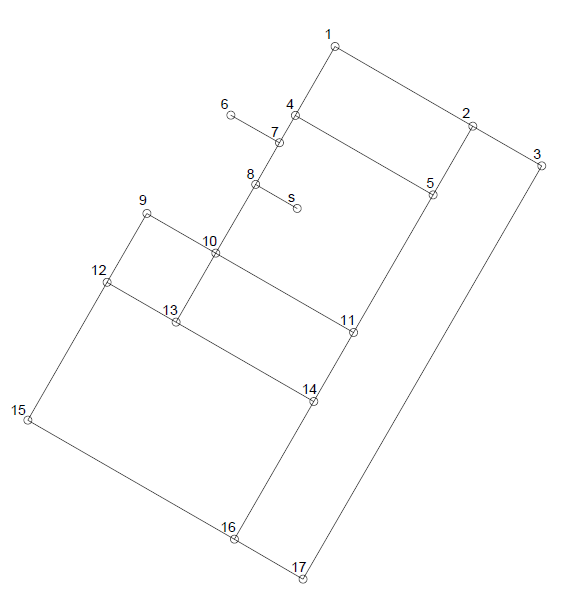
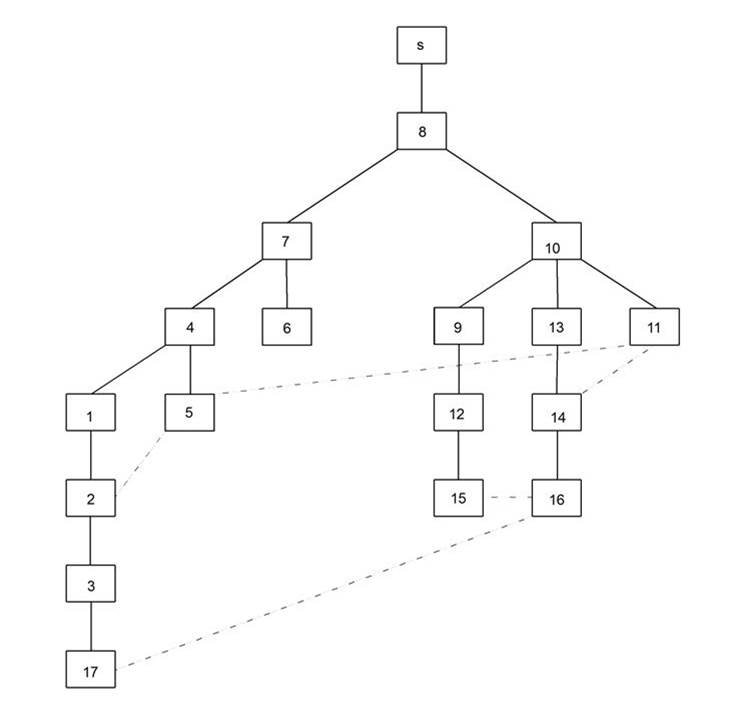
Figure 2 shows a breadth-first tree for the small network depicted in Figure 1, where the nontree edges are represented by dashed lines. If it is assumed that the pipes represented by nontree edges in the breadth-first tree carry no flow (are closed), then the breadth-first tree is exactly a hierarchical level tree of the water supply process in the network. Each edge (pipe) in this tree provides water to all of its descendant nodes. Therefore the flow rates in each pipe of the tree can be computed as the sum of the water demand of all descendant nodes of the first node of the pipe. The design water demand Q DMA corresponding to the given limit of service connections per DMA is then computed by the following equation:
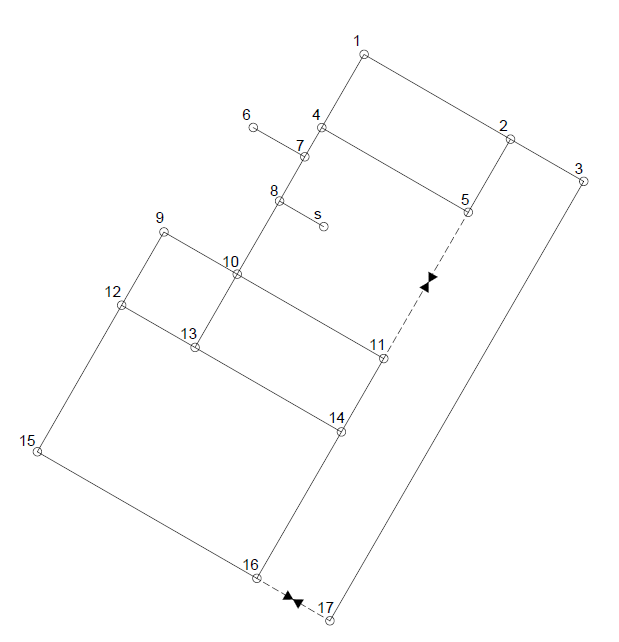
Where P is the design population, computed as the product of the given minimum number of service connections and the household crowding index; PCWU is the per capita daily water use, f d is the daily peaking factor, and f h is the hourly peaking factor. Every pipe of the hierarchical tree whose flow rate is greater than the design water demand per DMA computed by Eq (3) (but less than two times that flow rate) will be a DMA feeding pipe, where the corresponding DMA nodes will be all descendant nodes of its first node. The pipes to be closed in order to achieve the DMA isolation will be the nontree edges of the graph that connect the branch stemming from the given DMA feeding pipe to other tree branches. As an example, if the small network depicted in Figure 1 is to be divided in two DMAs, with the corresponding hierarchical tree in Figure 2, the DMA feeding pipes would be 8-7 and 8-10, and the pipes to close 5-11 and 17-16. It should be noted that the rest of the nontree edge pipes need not to be closed (that means the DMAs may contain internal closed loops). The resulting sectorization is shown in Figure 3. If, by some reason, the DMA need to be fed by two or more pipes, then the corresponding nontree edges are not closed, but it is case dependent.
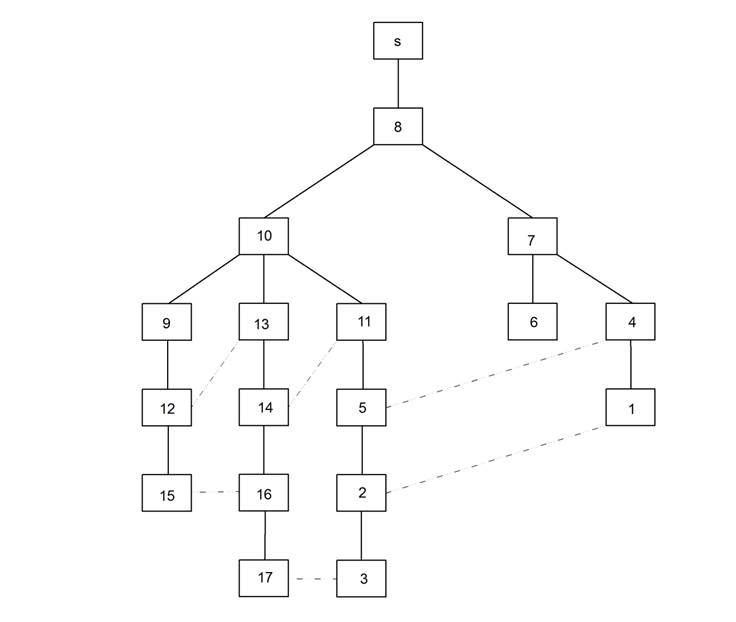
Although a breadth-first tree provides the shortest paths from the network source to each network node, in terms of number of graph edges, it is not unique but depends of the order in which the children nodes are put (pushed) into the queue. Figure 4 shows a different breadth-first tree for the network from Figure 1, obtained by using a different order of the children nodes in the queue. The resulting sectorization, shown in Figure 5 is not better balanced, compared to that of Figure 3. This provides a simple way of locally optimizing the resulting sectorization, sorting the nodes in the queue by their physical distance from the parent node. In principle, any other parameter, according to the sectorization criterion applied, can be used instead of the physical distance to sort them. This algorithm of making locally optimal choice at each stage represents a greedy algorithm. In many problems, a greedy strategy does not in general produce an optimal solution, but nonetheless a greedy heuristic may yield locally optimal solutions that approximate a global optimal solution. Future work is needed to consider the optimality conditions in the proposed DMA sectorization procedure.
Two slight modifications over the standard breadth-first traverse algorithm can speed-up the process and eventually improve the sought sectorization. Both of them avoid processing nodes or components of degree one and two since they do not influence the pipes to close in order to achieve the sectorization The first one is a preprocessing step that consists in removing all pendant edges (leafs) (in Figure1edge 7-6 is a pendant edge) and pendant subgraphs whose water demand is less than Q DMA . The second modification is that nodes of degree two are skipped during the breadth-first search. In both cases the water demand of the removed nodes must be considered.
After constructing the hierarchical water supply tree, and finding the flow rates in each pipe, the headloss in each pipe can be computed and the hydraulic feasibility of the proposed sectorization revised using a top-down computation of the hydraulic heads at each node starting from the head at the source node which is known.
Algorithmically speaking, the proposed procedure can be efficiently implemented in the following way:
Mark all graph edges (network pipes) as nontree edges.
Obtain the breadth-first tree by applying a breadth-first search. Mark each edge traversed as tree edge. The only other results that need to be saved in this step are the numbers of the children nodes, and the corresponding children pipes, for each node.
For each node, compute the sum of water demand of descendant nodes by a recursive top-down algorithm, i.e, sum the demand of children nodes to the demand of the children nodes of the children nodes (grandchildren nodes), and then to the demand of the children nodes of the grandchildren nodes, etc. The only information that is needed to implement such algorithm consists in the water demand and the numbers of the children nodes for each node.
For each node, compare the sum of water demand its descendant nodes to Q DMA . Assign the node as the entrance node of one DMA if that sum is greater to Q DMA and less than two times Q DMA .
Find the nodes belonging to the DMA defined in step 4, a by a top-down recursive algorithm, similar to that described in step 3. Mark those nodes as used nodes, so that they cannot be used in other DMAs.
Find the pipes to be closed to isolate the DMA defined in step 4, a by a top-down recursive algorithm, similar to that described in step 3.These are nontree pipes that have one only node that belongs to the corresponding DMA.
Besides their mathematical elegance and simplicity, graph theory based algorithms are more efficient in terms of speed of computation and storage requirements, compared to linear algebra topological matrix based algorithms (Giustolisi, Kapelan, & Savic, 2008; Giustolisi & Savic, 2010). The shortest paths and breadth-first search algorithm employed in the proposed procedure takes time O(V + E), linear in the size of the graph, and uses space O(V) to store the stack of vertices on the current search path as well as the set of already-visited vertices, where V is the number of Vertices (the nodes of a hydraulic network) and E is the number of Edges (the pipes of a hydraulic network), with no matrix storage and no floating point operations, typical for any linear algebra algorithm.
Case study
The proposed methodology has been applied to a real-case study of the water supply network of San Luis Rio Colorado, a Mexican city located in the north part of the state of Sonora on the Mexico-US border. The number of users connected to the city water distribution network is 48,400, of which 45,850 are residential, 2,445 are commercial, a 105 industrial type connections. The terrain is almost flat. The water supply sources consisted of 18 deep water wells, which were fully interconnected by the distribution network, at the beginning of the sectorization project, without water tanks. Some of the well pumps were equipped with variable speed drives that allowed the pumps to follow water demand variation and stop them when water demand was very low. The extent of the areas supplied by each water well was unknown, and it was suspected that some well pumps were frequently stopped, not because of low demand but because of higher hydraulic heads at other wells. The distribution network is about 50 years old, composed by 60 mm to 500 mm asbestos cement and polyvinyl chloride (PVC) pipes. The water supply sources are 10 deep water wells, without water tanks, fully interconnected by the distribution network before the sectorization actions took place. The service provided to the water users is continuous (24 hours). An all-pipe model, comprising 1,890 nodes and 2,681 pipes, was implemented for the existing network and for the proposed sectorization variants (Tzatchkov, Alcocer-Yamanaka, & Rodriguez-Varela, 2006).
i-DMA sectorization
Figure 6 shows the resulting i-DMA sectorization in 10 sectors, one for each water source (each water well) based on the minimum physical distance criterion, achieved by inserting 156 boundary valves that allow to isolate them completely. All isolated districts are supplied by a pair of water wells, except for i-DMA8 and i-DMA9.
DMA sectorization
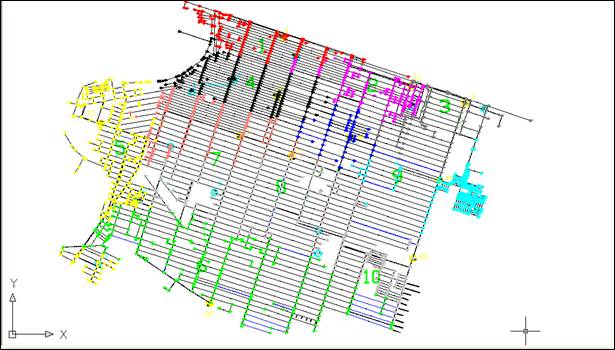
Figure 7 shows the resulting DMA sectorization for a per capita water use of 320 L/(inhabitant day), f d = 1.20, f h = 1.30, minimum number of service connections per DMA = 1,000 and household crowding index = 4.0. The minimum design flow per DMA, Q DMA , computed by Eq (3) with this data, equals 23.11 L/s. The network was sectorized in 30 DMAs.
Besides the distribution network partitioning, which is the focus of this paper, the design of sectorization involves other important aspects, such as the topography of the city, adjustment of the service pressure in each DMA according to the pressure at its critical node with eventual use of Pressure Reduction Valves (PRVs), constraints related to natural geographic boundaries and cost-benefit analysis of its implementation. A detailed procedure that considers these aspects is published by Gomes et al. (2012a).
Conclusions
Known graph partitioning techniques, commonly applied in distributed computing, are not directly applicable to water distribution network sectorization design. The main reason is that the partitioning criteria are different in the two cases. A few relevant methodologies have been proposed in the literature to design districts compatible with hydraulic performance, but they address mainly district metering areas (DMAs). In this paper, basic sectorization-specific graph partitioning criteria are outlined and algorithms for i-DMA and DMA sectorization that considers them are proposed, and applied to a case study of a real city water distribution networks. The proposed graph theory based algorithms are extremely efficient in terms of speed of computation and storage requirements Another advantage, specific for the proposed graph theory DMA sectorization method is that it provides a hierarchical level structure of the sectorized network showing directly the flow path from the sources to any network node, very useful in analyzing water quality and spread of contaminants.











 text new page (beta)
text new page (beta)