Introducción
El manejo forestal con fines maderables requiere mediciones precisas de los atributos o variables de los árboles para tener estimaciones confiables que faciliten una adecuada toma de decisiones. Entre las variables más importantes que se miden en los inventarios forestales están la altura total y el diámetro normal (a 1.3 m) de los individuos arbóreos, las cuales son básicas para estimar los volúmenes de madera o biomasa (Xionweng y Brockway, 2017); también son esenciales para estudios de crecimiento y rendimiento de árboles individuales, por lo que su utilidad es reconocida en la ejecución del manejo técnico (Peng et al., 2001; Osman et al., 2013).
Sin embargo, la medición en campo de la altura total de los árboles en pie, a diferencia del diámetro normal, implica dificultades prácticas que incrementan los tiempos y costos del inventario (Trincado y Leal, 2006; Sharma, 2009). Además, su medición está propensa a errores, en particular en bosques con sotobosques densos o donde coexisten árboles de distintas edades, especies, tamaños, vigor o clases de copa (Temesgen et al., 2014; Arnoni et al. 2016).
Una alternativa que supera las limitaciones referidas consiste en estimar la altura total como una función del diámetro normal, el cual se mide con mayor facilidad y precisión; para ello se utilizan modelos matemáticos que relacionan las dos variables (Trincado y Leal, 2006). Con ese fin se han desarrollado modelos lineales y no lineales, en su mayoría asintóticos, que permiten calcular con certidumbre la altura total de un árbol en función de su diámetro normal (Rijal et al., 2012; Arnoni et al., 2016; Duan et al., 2018). Clutter et al. (1983), Ahmadi et al. (2013) y Mehtätalo et al. (2015) consideran que la estimación a través de modelos no lineales es mucho mejor que con modelos lineales.
Asimismo, se recomienda que los modelos sean determinados por separado para cada especie de interés (Misir, 2010; VanderSchaaf, 2014; Sharma y Breidenbach, 2015) y por región (Crecente-Campo et al., 2010; Coble y Young-Jin, 2011). Algunos estudios señalan que estas relaciones son particulares y dependientes de las condiciones del sitio, por lo que es común obtener modelos locales (Corral-Rivas et al., 2014) de aplicación restringida, o bien incorporar en los modelos algunas características del sitio o atributos del rodal (i.e. la densidad, altura dominante, estructura, entre otras) que también influyen en la relación altura-diámetro (Gonzalez-Benecke et al., 2013; Ahmadi y Alavi, 2016), lo que permite obtener modelos generalizados (Corral-Rivas et al., 2014; Hernández et al., 2015) cuyo ámbito de aplicación es más amplio.
En la actualidad, existen varios modelos para describir de manera apropiada el comportamiento de la altura total en función del diámetro normal, los cuales se han usado ampliamente en otros países (Arnoni et al., 2016; Ahmadi y Alavi, 2016). Por ejemplo, modelos como los de Chapman-Richards, Weibull, Schnute, el logístico modificado y la función exponencial son de amplia aplicación por sus capacidades predictivas (Peng et al., 2001; Temesgen et al., 2014; Ahmadi y Alavi, 2016).
Sin embargo, a pesar de su relevancia, en México son escasos los estudios en los que se estima la altura total en función del diámetro normal; por ejemplo, Valdez-Lazalde y Lynch (2000) ajustaron dicha relación con modelos no lineales para Pinus patula Schiede ex Schltdl. et Cham. en el estado de Puebla; Hernández et al. (2015) compararon 13 modelos generalizados para analizar la relación diámetro-altura para Pinus teocote Schtldl. et Cham.; en tanto que Corral-Rivas et al. (2014) probaron 27 modelos y determinaron que el modelo Bertalanffy-Richards fue el que presentó mejores ajustes para seis de 13 grupos de especies de coníferas y latifoliadas.
Pinus montezumae Lamb. y P. teocote son especies de importancia comercial maderable, de distribución amplia en el país. El primero, alcanza en algunos sitios hasta 35 m de altura y diámetros de 1.0 m; en tanto, P. teocote es un árbol de porte mediano, con copa redondeada e irregular, que alcanza entre 10 y 20 m de altura, aunque los valores máximos registrados son de 75 cm de diámetro y hasta 25 m en altura (Perry, 1991; Martínez, 1992). Los dos taxones se aprovechan de manera comercial en varias regiones de México, como es el caso de la región Calpulalpan-Nanacamilpa en el estado de Tlaxcala, cuyo historial de manejo forestal se remonta a más de tres décadas (Guerra et al., 2008). Debido a su amplia distribución geográfica en el territorio nacional, es posible esperar variaciones importantes en su alometría; no obstante, en la región de estudio se carece de modelos que describan su relación altura total-diámetro normal (h-d).
Por lo anterior, el objetivo del presente estudio fue analizar 15 modelos estadísticos y proponer el de mejor calidad de ajuste para estimar la altura total en función del diámetro normal para árboles de Pinus montezumae y P. teocote en la región forestal de Nanacamilpa, en Tlaxcala, México.
Materiales y Métodos
Área de estudio
La región de estudio se ubica en la parte occidental de Tlaxcala, México. Limita al norte con la región de Calpulalpan y al sur con el estado de Puebla; la región de Nanacamilpa está incluida en su totalidad dentro de la región fisiográfica del Eje Neo-volcánico Transversal, entre las coordenadas geográficas 19°27'30" y 19°30'38" de latitud norte y 98°38'17" y 98°32'17” de longitud oeste (Figura 1). Presenta un intervalo altitudinal de 2 600 a 3 300 m; con clima del tipo C(w2), templado-subhúmedo, con lluvias en verano, temperatura media anual de entre 12 °C y 18 °C (Inegi, 2009).
Los tipos de vegetación más representativos corresponden a los bosques de coníferas y latifoliadas, cuyas especies más sobresalientes son Pinus montezumae, P. teocote, P. pseudostrobus Lindl., Abies religiosa (Kunth) Schltdl. & Cham. y Quercus laurina Bonpl., las cuales se desarrollan sobre cambisoles húmicos y eutricos, así como en andosoles húmicos de texturas arcillosa y arcillo-limosas (Inegi, 2009). El manejo forestal en la región se desarrolló, inicialmente, bajo el sistema regular que incluye cortas de regeneración y aclareos a lo largo del turno (Guerra et al., 2008).
Obtención de datos de campo
La información de campo se obtuvo a través del levantamiento de sitios de muestreo para inventario, cuya forma y distribución se basó en el diseño utilizado en el Inventario Nacional Forestal y de Suelos que considera a un conglomerado como unidad primaria, compuesto por cuatro parcelas de 400 m2 como unidades de muestreo secundarias (Conafor, 2012). Se establecieron 16 conglomerados distribuidos de forma sistemática en el área de estudio, en los que se realizó la medición de las variables dasométricas de interés de todos los árboles vivos, completos y sanos, cuyo diámetro normal (1.3 m del nivel del suelo) fuera igual o mayor a 7.5 cm. Además, se incluyeron 186 árboles de P. teocote con diámetros superiores a 30 cm, que fueron escasos en las parcelas de muestreo.
El diámetro normal se midió con una cinta diamétrica marca Richter ® de 5 m, en tanto que la altura total se obtuvo con un hipsómetro digital Vertex III Haglof ® con un transmisor ultrasónico T3. Aunque se consideraron todas las especies arbóreas de cada unidad secundaria de muestreo, para el estudio solo se integraron los datos de P. montezumae y P. teocote, por ser los taxa mejor representados en el área, cuya densidad promedio es de 231 y 112 árboles ha-1, respectivamente. Con esta información se conformó una base de datos para el análisis de regresión, que incluyó un total de 583 pares de datos de diámetro normal-altura total para P. montezumae y de 468 pares para P. teocote. Los estadísticos descriptivos se presentan en el Cuadro 1.
Cuadro 1 Estadísticos básicos de las variables analizadas de las dos especies estudiadas.
| Estadístico | Pinus montezumae | Pinus teocote | ||
|---|---|---|---|---|
| d (cm) | h (m) | d (cm) | h (m) | |
| Mínimo | 7.5 | 2.5 | 7.5 | 4.9 |
| Máximo | 80.9 | 42 | 80.9 | 32.1 |
| Promedio | 26.7 | 17.73 | 24.9 | 15.7 |
| Desviación estándar | 19.962 | 10.502 | 17.102 | 6.341 |
| Coeficiente de variación | 0.75 | 0.59 | 0.69 | 0.40 |
| Curtosis | -0.88 | -1.32 | 0.13 | -0.52 |
| Asimetría | 0.76 | 0.50 | 1.09 | 0.75 |
d = Diámetro normal (1.30 m); h = Altura total
Análisis estadístico
Se ajustaron los datos altura-diámetro de P. montezumae y P. teocote mediante análisis de regresión lineal y no lineal; se probaron 14 modelos no lineales utilizados de manera extensa en la literatura especializada sobre biometría forestal (Cuadro 2). Debido a que en las bases de datos solo se incluyeron árboles con diámetro normal ≥7.5 cm y, por tanto, no se midieron diámetros cercanos o iguales a cero, en ningún caso se integró de manera explícita la constante de 1.3 en los modelos, la cual condiciona a que la altura estimada sea de 1.3 m cuando el diámetro normal es igual a cero. Además, en términos prácticos, pocas veces se requiere estimar alturas de diámetros cercanos a cero, por lo que su interés es teórico (Trincado y Leal, 2006).
Cuadro 2 Modelos utilizados para determinar la altura total a partir de diámetro normal de Pinus montezumae Lamb. y Pinus teocote Schiede ex Schltdl.
| Identificador | Modelo | Referencia |
|---|---|---|
| (M1) |
|
Clutter et al. (1983) |
| (M2) |
|
Temesgen et al. (2014) |
| (M3) |
|
Temesgen et al. (2014) |
| (M4) |
|
Castillo-Gallegos et al. (2018) |
| (M5) |
|
Castillo-Gallegos et al. (2018) |
| (M6) |
|
Castillo-Gallegos et al. (2018) |
| (M7) |
|
Sharma (2009) |
| (M8) |
|
Castillo-Gallegos et al. (2018) |
| (M9) |
|
García et al. (2017) |
| (M10) |
|
García et al. (2017) |
| (M11) |
|
García et al. (2017) |
| (M12) |
|
García et al. (2017) |
| (M13) |
|
Castillo-Gallegos et al. (2018) |
| (M14) |
|
Castillo-Gallegos et al. (2018) |
| (M15) |
|
Castillo-Gallegos et al. (2018) |
h = Altura total; d = Diámetro normal; β i = Parámetros del modelo.
Aunque la mayoría de los estudios sobre la relación h-d consideran modelos no lineales por ser los que mejor describen el crecimiento, en este caso se consideró un modelo con estructura lineal en los parámetros (M10), ya que en algunos casos ha mostrado buenos resultados en el ajuste de este tipo de relaciones (García et al., 2017).
El análisis de regresión se realizó con el programa SAS® ver 9.3 (SAS, 2011). Para los modelos no lineales se usó el procedimiento MODEL, mediante cuadrados mínimos ordinarios, mientras que para el modelo lineal se empleó el procedimiento REG del mismo programa de análisis estadístico. La bondad de ajuste de cada modelo se evaluó con el coeficiente de determinación corregido por el número de parámetros (R2 adj) como indicador de la proporción de la varianza explicada por la variable independiente, el sesgo, la raíz del error cuadrático medio (RECM), la suma de cuadrados del error (SCE), el cuadrado medio del error (CME), la significancia de los estimadores y el criterio de información de Akaike (AIC). Este último, es un criterio muy confiable al comparar modelos con diferente número de parámetros (Sharma, 2009).
Para mayor objetividad en la selección del mejor modelo por especie, los criterios de bondad de ajuste indicados se jerarquizaron con base en el procedimiento descrito por Tamarit et al. (2014), para generar un índice de calidad cuyo valor total permitió identificar más fácilmente al modelo con el mejor ajuste en cada caso. Aunque los criterios de ajuste estadístico fueron la base principal para la selección del mejor modelo, también se analizó su congruencia biológica, dado que esta es una característica deseable en cualquier modelo de crecimiento (Sharma, 2009). Algunos autores han indicado la importancia de considerar la capacidad predictiva de los modelos, en particular en alturas de árboles de mayores dimensiones (Moore et al., 1996; Zhao et al., 2006), lo que implica la búsqueda de un comportamiento razonable de la curva ajustada en todo el intervalo de datos, con atención especial en el límite superior.
Debido a lo anterior, el comportamiento asintótico de la curva de cada especie se juzgó en función de los valores máximos de crecimiento en altura citados en la literatura y en los datos observados. Así, la descripción grafica del modelo dentro y fuera del intervalo de los datos observados fue un criterio adicional para la selección. Asimismo, se verificó el cumplimiento de los supuestos básicos de la regresión (i.e. la normalidad en la distribución de los errores), a través de la prueba de Shapiro-Wilk, junto con el análisis gráfico de los residuales para observar las tendencias antes de hacer inferencias sobre los estimadores de los parámetros en cada modelo (Kutner et al., 2005).
Resultados y Discusión
Pinus montezumae
El ajuste de los modelos analizados se muestra en el Cuadro 3. Se observa que, en general, todos los modelos probados para P. montezumae, sin importar su forma y número de parámetros, mostraron buenos ajustes dado que la varianza explicada (R2 adj) por la variable independiente fue mayor a 89 % en todos los casos.
Cuadro 3 Estadísticos de bondad de ajuste de los modelos analizados para Pinus montezumae Lamb.
| Modelo | SCE | CME | RECM | R2 adj | Sesgo | AIC | Calificación Total |
|---|---|---|---|---|---|---|---|
| M1 | 5 557.8 | 9.58 | 3.10 | 0.91 | 0.03 | 1 320.53 | (29) |
| M2 | 5 538.2 | 9.55 | 3.09 | 0.91 | 0.05 | 1 318.48 | (28) |
| M3 | 5 582.9 | 9.63 | 3.10 | 0.91 | 0.01 | 1 323.16 | (31) |
| M4 | 5 772.1 | 9.95 | 3.16 | 0.91 | 0.02 | 1 342.59 | (58) |
| M5 | 5 621.4 | 9.69 | 3.11 | 0.91 | 0.04 | 1 327.16 | (40) |
| M6 | 5 747.6 | 9.89 | 3.15 | 0.91 | -0.06 | 1 338.11 | (47) |
| M7 | 5 487.9 | 9.46 | 3.08 | 0.91 | 0.04 | 1 313.16 | (21) |
| M8 | 5 621.4 | 9.69 | 3.11 | 0.91 | 0.04 | 1 327.16 | (47) |
| M9 | 5 936.8 | 10.24 | 3.20 | 0.91 | 0.0004 | 1 358.99 | (64) |
| M10 | 5 477.7 | 9.44 | 3.07 | 0.91 | 0.001 | 1 312.07 | (10) |
| M11 | 6 803.6 | 11.71 | 3.42 | 0.89 | 0.20 | 1 436.44 | (90) |
| M12 | 6 357.6 | 10.94 | 3.31 | 0.90 | -0.09 | 1 396.91 | (66) |
| M13 | 6 634.2 | 11.42 | 3.38 | 0.90 | 0.19 | 1 421.74 | (84) |
| M14 | 5 858.9 | 10.08 | 3.18 | 0.91 | -0.002 | 1 349.29 | (58) |
| M15 | 5 656.3 | 9.75 | 3.12 | 0.91 | 0.02 | 1 330.77 | (47) |
R 2 adj = Coeficiente de determinación ajustado; RMSE = Raíz del error cuadrático medio; SSE = Suma de cuadrados del error; MSE = Error cuadrado medio; AIC = Criterio de información de Akaike.
El índice de calidad de ajuste, dado por la calificación total de cada modelo, evidencia que los cinco mejores modelos son M10, M7, M2, M1 y M3 (todos con tres parámetros) por ser los que menores valores acumularon; es decir, son los que mostraron los mejores valores de todos los criterios de ajuste. Cabe hacer notar que los modelos de dos parámetros (M6, M11-M14) tuvieron valores pobres en los errores (SCE, CME y RECM) por lo que sus calificaciones globales resultaron, en general, menos adecuadas que los de tres parámetros. Además, tres de ellos no cumplieron con el supuesto de normalidad en los residuales, por lo que fueron descartados en la selección.
Aunque la evaluación con el índice sugiere cuales modelos tuvieron mejor comportamiento estadístico, al observar la significancia de los estimadores de cada modelo se observa que todos resultaron significativos, excepto el mejor calificado (M10), que presenta un parámetro (b0) no significativo (Cuadro 4), razón por la que también se desestimó.
Cuadro 4 Valores y significancia de los estimadores de los modelos analizados para Pinus montezumae Lamb.
| Modelo | b 0 | Pr > |t| | b 1 | Pr > |t| | b 2 | Pr > |t| |
|---|---|---|---|---|---|---|
| M1 | 40.145 | <.0001 | 0.031 | <0.0001 | 0.144 | 0.0039 |
| M2 | 38.681 | <.0001 | -0.018 | <0.0001 | 1.135 | <0.0001 |
| M3 | 4.049 | <.0001 | -38.875 | <0.0001 | 10.547 | <0.0001 |
| M4 | 113.019 | <.0001 | 6.653 | <0.0001 | 0.412 | <0.0001 |
| M5 | 1.219 | <.0001 | 1.623 | <0.0001 | 0.019 | <0.0001 |
| M6 | 72.625 | <.0001 | 71.206 | <0.0001 | ||
| M7 | 0.826 | <.0001 | 1.037 | <0.0001 | -0.002 | <0.0001 |
| M8 | 51.746 | <.0001 | 0.012 | <0.0001 | 1.219 | <0.0001 |
| M9 | -15.519 | 0.0009 | 9.941 | 0.0012 | 0.388 | <0.0001 |
| M10 | 0.188 | 0.6196 | 0.909 | <0.0001 | -0.006 | <0.0001 |
| M11 | 42.222 | <.0001 | -16.945 | <0.0001 | ||
| M12 | 0.583 | <.0001 | 0.716 | <0.0001 | ||
| M13 | 42.893 | <.0001 | 17.863 | <0.0001 | ||
| M14 | 1.276 | <.0001 | 2.313 | <0.0001 | ||
| M15 | 38.664 | <.0001 | -0.018 | <0.0001 | 1.135 | <0.0001 |
b 0 , b 1 y b 2 = Coeficientes de regresión; Pr>[t] = Probabilidad de t.
Los cuatro restantes mejores modelos cumplieron con el supuesto de normalidad de residuales (no se rechaza H0, p<0.05) (Figura 2). Corral-Rivas et al. (2014) al estudiar la relación h-d para 25 especies en el norte de México, indican que el modelo local de Bertalanffy-Richards es el más consistente al mostrar valores de R2 de entre 0.6 y 0.8 en siete especies de pino. Los resultados de este trabajo coinciden con el estudio referido, ya que el modelo (M1) junto con el de Yang (M2), cuya estructura es parecida, presentaron resultados muy similares, con valores de R2 adj de 0.91. Asimismo, Castillo-Gallegos et al. (2018) determinaron que el modelo local de Richards fue el mejor para modelar la relación h-d para P. chiapensis (Martínez) Andresen en Veracruz, México, pero con valores de R2 mucho menores. Con base en lo anterior, el criterio final para decidir cuál es el mejor modelo para P. montezumae en el presente trabajo fue la congruencia biológica, mediante el análisis de su comportamiento gráfico.
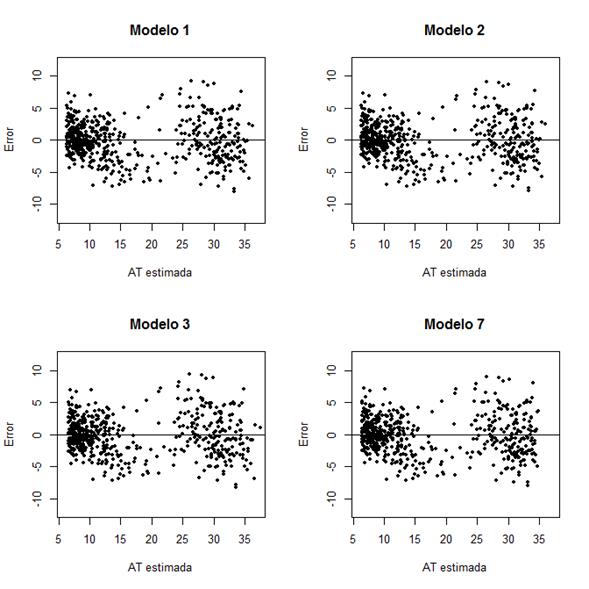
Figura 2 Distribución de residuales de los cuatro mejores modelos de altura-diámetro ajustados para Pinus montezumae Lamb.
En el intervalo de datos observados, los cuatro mejores modelos mostraron un comportamiento muy parecido hasta un diámetro aproximado de 60 cm, después del cual las proyecciones de altura se diferencian (Figura 3), en particular con el M3 que predice valores mayores de altura, sin mostrar una tendencia asintótica, aun fuera del intervalo de datos. Por el contrario, el modelo de Sharma (M7) indica valores más bajos y un máximo de 35 m de altura para diámetros ligeramente superiores a 80 cm, después de los cuales predice alturas menores, lo que puede no ser del todo aceptable para P. montezumae.
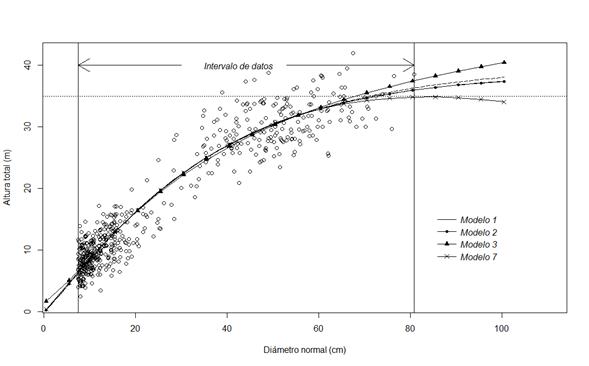
Figura 3 Trayectorias de las curvas generadas con los mejores modelos de altura-diámetro y datos observados para Pinus montezumae Lamb.
Al respecto, Zhao et al. (2006) consideran que entre los atributos deseables de las ecuaciones altura-diámetro están el de alcanzar una asíntota en diámetros mayores y presentar siempre una pendiente positiva, ninguno de las cuales se observó con el M7. En tanto, los modelos de Richards (M1) y de Yang (M2) se comportan de manera similar, incluso en el límite superior de los datos y muestran una tendencia asintótica alrededor de 38 m de altura, en diámetros cercanos a 100 cm; esto es razonable, desde el punto de vista biológico, para árboles de P. montezumae, en particular en regiones con buena calidad de sitio (Rodríguez et al., 1988). Sin embargo, dado que el modelo de Yang (M2) es más conservador, además de sus mejores valores de ajuste, en comparación con el de Richards (M1), se considera como el más apto para estimar la altura total en árboles de P. montezumae en la región de estudio y queda expresado en la siguiente forma:
Donde:
h = Altura total
d = Diámetro normal
Pinus teocote
En general, los valores de ajuste de los modelos probados para la especie también fueron adecuados, a partir de que son modelos locales (Cuadro 5). Hernández et al. (2015) estimaron alturas para P. teocote mediante ecuaciones generalizadas en el estado de Hidalgo, y obtuvieron valores de R 2 adj de 0.93. Bajo el procedimiento de jerarquización de los criterios seguidos en el presente estudio, se observa que el modelo con mejor ajuste a los datos, por su menor valor en el índice, es el modelo cuadrático (M10), cuyo coeficiente de determinación ajustado (R² adj) es de 0.87, el cual supera al registrado por Corral-Rivas et al. (2014) para la misma especie (R2<0.7) en el norte de México.
Cuadro 5 Estadísticos de bondad de ajuste de los modelos analizados para Pinus teocote Schiede ex Schltdl.
| Modelo | SCE | CME | RECM | R2 adj | Sesgo | AIC | Calificación Total |
|---|---|---|---|---|---|---|---|
| M1 | 2 569.5 | 5.53 | 2.35 | 0.86 | 0.01 | 803.00 | (37) |
| M2 | 2 570.9 | 5.53 | 2.35 | 0.86 | 0.02 | 803.27 | (51) |
| M3 | 2 518.0 | 5.42 | 2.33 | 0.87 | 0.002 | 793.53 | (12) |
| M4 | 2 841.5 | 6.11 | 2.47 | 0.85 | 0.57 | 850.10 | (80) |
| M5 | 2 570.9 | 5.53 | 2.35 | 0.86 | 0.01 | 803.26 | (48) |
| M6 | 2 793.7 | 6.00 | 2.45 | 0.85 | 0.09 | 840.15 | (72) |
| M7 | 2 568.4 | 5.52 | 2.35 | 0.86 | 0.01 | 802.80 | (28) |
| M8 | 2 570.9 | 5.53 | 2.35 | 0.86 | 0.01 | 803.26 | (55) |
| M9 | 2 568.5 | 5.52 | 2.35 | 0.86 | -0.001 | 802.82 | (25) |
| M10 | 2 505.0 | 5.39 | 2.32 | 0.87 | 0.004 | 791.10 | (9) |
| M11 | 3 835.9 | 8.23 | 2.87 | 0.80 | 0.11 | 988.53 | (89) |
| M12 | 2 571.1 | 5.52 | 2.35 | 0.86 | 0.003 | 801.29 | (25) |
| M13 | 3 726.6 | 8.00 | 2.83 | 0.80 | 0.11 | 975.00 | (83) |
| M14 | 2 733.2 | 5.87 | 2.42 | 0.85 | 0.04 | 829.91 | (66) |
| M15 | 2 569.7 | 5.53 | 2.35 | 0.86 | 0.01 | 803.04 | (40) |
R 2 adj = Coeficiente de determinación ajustado; RMSE = Raíz del error cuadrático medio; SSE = Suma de cuadrados del error; MSE = Error cuadrado medio; AIC = Criterio de información de Akaike.
Con base en el sistema de calificación, después del M10 los mejores modelos resultaron ser M3, M12, M9 y M7; sin embargo, respecto a las pruebas de hipótesis sobre los estimadores, el valor de b 0 con el M9, y de b 2 con el M7 no fueron significativos (P<0.05) (Cuadro 6), por lo que no se consideraron para su análisis posterior. En todo caso, M3 y M12 se ubicaron en segundo y tercer lugar, respectivamente (Cuadro 5), con la ventaja de que todos sus coeficientes fueron significativos (p<0.05) y en ambos casos se cumple el supuesto de normalidad en los residuales, con base en los gráficos de dispersión (Figura 4) y el estadístico de SW (>0.97).
Cuadro 6 Valores y significancia de los estimadores de los modelos analizados para Pinus teocote Schiede ex Schltdl.
| Modelo | b 0 | Pr > t | b 1 | Pr > t | b 2 | Pr > t |
|---|---|---|---|---|---|---|
| M1 | 85.542 | 0.2886 | 0.002 | 0.6007 | -0.743 | <0.0001 |
| M2 | 392.281 | 0.8367 | -0.007 | 0.8331 | 0.567 | <0.0001 |
| M3 | 4.028 | <0.0001 | -63.758 | <.0001 | 27.165 | <0.0001 |
| M4 | 928.458 | 0.6718 | 6.180 | 0.0031 | 0.132 | 0.0889 |
| M5 | 0.564 | <0.0001 | 0.363 | <.0001 | 0.001 | 0.8711 |
| M6 | 41.496 | <0.0001 | 34.639 | <.0001 | ||
| M7 | 2.651 | <0.0001 | 0.576 | <.0001 | -0.0002 | 0.4754 |
| M8 | 878.678 | 0.8638 | 0.003 | 0.8613 | 0.565 | <0.0001 |
| M9 | 1.197 | 0.5005 | 2.252 | 0.0033 | 0.596 | <0.0001 |
| M10 | 5.085 | <0.0001 | 0.527 | <.0001 | -0.003 | <0.0001 |
| M11 | 30.357 | <0.0001 | -12.421 | <.0001 | ||
| M12 | 1.030 | <0.0001 | 0.553 | <.0001 | ||
| M13 | 30.800 | <0.0001 | 13.130 | <.0001 | ||
| M14 | 2.184 | <0.0001 | 1.768 | <.0001 | ||
| M15 | 0.0002 | 0.6991 | 0.177 | 0.0017 | 0.572 | <0.0001 |
b 0 , b 1 y b 2 = Coeficientes de regresión; Pr>[t] = Probabilidad de t.
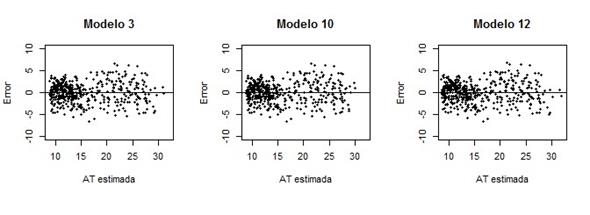
Figura 4 Distribución de residuales de los tres mejores modelos de altura-diámetro ajustados para Pinus teocote Schiede ex Schltdl.
De forma gráfica, los modelos M3, M10 y M12 describieron trayectorias similares hasta un diámetro aproximado de 65 cm (Figura 5), después del cual solo el modelo M10 presentó un descenso en el valor de la pendiente de la curva, mientras que M3 y M12 mantuvieron su trayectoria ascendente, aun fuera del intervalo de los datos. Es evidente, que con esos dos modelos hay una tenencia a sobrestimar la altura total (>32 m) para árboles con diámetros cercanos a 80 cm, por lo que se consideran no adecuados para modelar esta relación. La tendencia mostrada por la curva que genera el modelo M10 parece más razonable y lógica para P. teocote, cuyos diámetros y alturas máximas difícilmente pueden ser mayores a 85 cm y 32 m, respectivamente. Por ejemplo, Hernández et al. (2015) documentan valores máximos de 72 cm en diámetro y 31 m de altura para la misma especie.
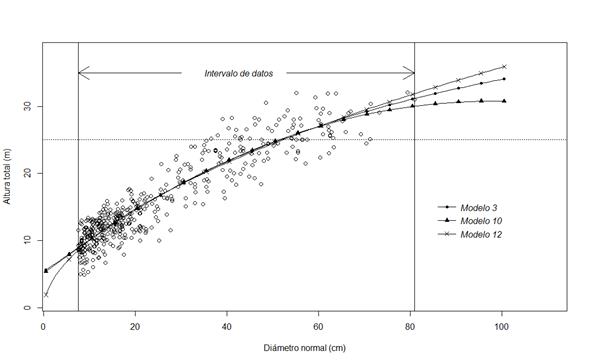
Figura 5 Trayectorias de las curvas generadas con los mejores modelos de altura-diámetro y datos observados para Pinus teocote Schiede ex Schltdl.
Por lo tanto, la ecuación final (Modelo 10) para estimar la altura total de árboles de P. teocote a partir del diámetro normal en la región de estudio queda expresada de la siguiente manera:
Donde:
h = Altura total
d = Diámetro normal
Los modelos locales de altura-diámetro seleccionados para Pinus montezumae y P. teocote son específicos de las condiciones propias de los bosques de la región occidental del estado de Tlaxcala. Por sus valores adecuados de ajuste estadístico y su congruencia biológica, pueden ser aplicados en la práctica silvícola de dicha zona. Además, serán útiles en futuras investigaciones; por ejemplo, para generar sistemas de crecimiento y rendimiento maderable de las dos especies de Pinus estudiadas, pero siempre restringidas a la misma área geográfica.
Conclusiones
En general, los modelos probados para las dos especies tienen buenos ajustes, ya que explican más de 80 % de la varianza de la altura total en ambos casos. Los mejores modelos para estimar la altura total en función del diámetro normal para árboles individuales son el de Yang (M2) para Pinus montezumae y el cuadrático (M10) para P. teocote, en virtud de su mejor calidad de ajuste y de la congruencia biológica mostrada en la descripción grafica de la relación altura-diámetro. Estos modelos locales permitirán realizar estimaciones de altura total de los árboles con precisiones superiores a 87 % en bosques de P. montezumae y P. teocote bajo manejo en la región de Nanacamilpa del estado de Tlaxcala.











 texto en
texto en