Services on Demand
Journal
Article
Indicators
Related links
Share
Revista mexicana de ciencias agrícolas
Print version ISSN 2007-0934
Rev. Mex. Cienc. Agríc vol.15 n.2 Texcoco Feb./Mar. 2024 Epub June 21, 2024
https://doi.org/10.29312/remexca.v15i2.3634
Articles
Treatments nested within a balanced complete block group arrangement
1Facultad de Ciencias Agrícolas-Centro de Investigación y Estudios Avanzados en Fitomejoramiento-Universidad Autónoma del Estado de México. Campus Universitario ‘El Cerrillo’. El Cerrillo Piedras Blancas, Toluca, Estado de México, México. AP. 435. Tel. 722 2965518, ext. 148. (djperezl@uaemex.mx; jhernandeza@uaemex.mx; jrfrancom@uaemex.mx; mrubia@uaemex.mx; abalbuenam@uaemex.mx).
When designing and analyzing an experiment or a series of trials in time or space, it could be of great relevance to subdivide the number of treatments by forming groups in which some important difference between them and some similarity within them are considered. This study analyzed the case presented by Gomez and Gomez (1984) regarding the grain yield recorded in 45 rice varieties, classified into three groups; their statistical model for an experimental design of randomized complete blocks was presented, complementary formulas were included to calculate the sums of squares with the methodologies of least squares and quadratic or matrix forms, and the procedure to generate an output if InfoStat were applied is proposed. In addition, other ways are mentioned to calculate degrees of freedom if the experimental area is divided into main unit and subunit, and those corresponding to the model residual or error b, which simplify manual calculations. The formulas for both methodologies were standardized based on the formal use of the symbology used in the sum and point notations; their quadratic forms are presented based on the latter. The difference between a conventional analysis of variance and the one considered in this paper, based on the sums of squares, is discussed. Finally, it is indicated how to apply Tukey’s test for the comparison of means of varieties within each group if InfoStat is used. It is also recommended to use a matrix calculator to solve calculations when using quadratic forms, which is freely available on their website.
Keywords: InfoStat; least squares; quadratic forms; randomized complete block design
Cuando se diseña y analiza un experimento o una serie de ensayos en tiempo o espacio podría ser de gran relevancia realizar una subdivisión del número de tratamientos por medio de la formación de grupos en los que se considere alguna diferencia importante entre éstos y alguna similitud dentro de ellos. En este estudio se analizó el caso presentado por Gomez y Gomez (1984) con relación al rendimiento de grano registrado en 45 variedades de arroz, clasificadas en tres grupos, se presentó su modelo estadístico para un diseño experimental de bloques completos al azar, se incluyeron fórmulas complementarias para calcular las sumas de cuadrados con las metodologías de mínimos cuadrados y formas cuadráticas o matriciales y se propone el procedimiento para generar una salida si fuera aplicado InfoStat. Adicionalmente, son mencionadas otras formas para calcular grados de libertad si el área experimental es dividida en unidad principal y subunidad, así como los correspondientes al residual del modelo o error b, las cuales simplifican los cálculos manuales. Se homologaron las fórmulas para ambas metodologías partiendo del uso formal de la simbología utilizada en las notaciones suma y punto, con base en éstas últimas se presentan sus formas cuadráticas. Se discute la diferencia entre un análisis de varianza convencional y el que es considerado en este trabajo, con base en las sumas de cuadrados finalmente, se indica cómo aplicar la prueba de Tukey para la comparación de medias de variedades dentro de cada grupo si es utilizado InfoStat. También se recomienda el uso de una calculadora de matrices para solucionar cálculos cuando se utilizan formas cuadráticas, la cual se encuentra disponible gratuitamente en su sitio WEB.
Palabras clave: diseño de bloques completos al azar; formas cuadráticas; InfoStat; mínimos cuadrados
Introduction
The design, analysis, and interpretation of the data provided by an experiment are very valuable tools in agronomic research when statistical inferences are supported by reliable information (Sahagún, 1997; Sahagún, 2007; Montgomery, 2009). The general steps considered during these include definition of the problem, justification of the trial, approach and critical analysis of the scientific objectives and hypotheses, structure of treatments, number of repetitions and size of the experimental unit, choice of experimental design, local control of heterogeneity associated with adjacent plots or between those receiving the same treatment, nature and type of variable recorded, material and instruments used, applicable statistical methodologies, research protocol to be applied, discussion of results, derivation of conclusions, and final report (Gomez and Gomez, 1984; Martinez, 1988; Little and Hills, 2008).
The following should also be considered: appropriate statistical model, type of factor considered (fixed, random, or mixed), existence or absence of orthogonality, nesting or crossover relationships between the factors studied and their interactions, dependence between mean squares and their mathematical expectations with the relevant hypothesis tests, software used, and statistical inference, among others (Sahagún, 1998; Piepho et al., 2003; Restrepo, 2007a, 2007b). In addition, the fact of carrying out the analyses without and with subsampling within the experimental units should be weighed and justify the case when choosing a small sample size, it is decided or not to estimate effects instead of variances (Zamudio and Alvarado, 1996; Cochran and Cox, 2004; González et al., 2023).
The present study will analyze the case presented by Gomez and Gomez (1984), who grouped 45 varieties of rice (Oryza sativa L.) into three groups, each with 15 genetic materials; in the experimental design of randomized complete blocks that they used, in an arrangement of balanced complete block, they used three repetitions per treatment to evaluate grain yield.
They did not present their statistical model, but the total variability that was estimated in this quantitative characteristic was divided into differences between groups, between repetitions, error a, between treatments within each group, and error b or residual of the model. As there is no permission to use the data, only additional information will be provided for the analysis of this type of arrangement of experimental units, with emphasis on their statistical model, alternative formulas to calculate the sum of squares with two methodologies, and a procedure that will generate an output using InfoStat, for an analysis of variance and a comparison of means of varieties within groups applying Tukey’s test.
Materials and methods
Statistical model
Based on the guide provided by Sahagún (1998); Piepho et al. (2003); Restrepo (2007), among others, the model that was constructed was: Xijk = µ+ Gi + Rj + (GR)ij + τk(i) + εijk
Where: X is the grain yield in rice or any other quantitative variable of interest; μ is the arithmetic mean of the rt data; Gi is the effect caused by the i-th group; Rj is the contribution of the j-th repetition; (GR)ij is the interaction caused by the i-th group with the j-th repetition or error a; τk(i) is the effect caused by the k-th treatment nested within the i-th group; and εijk is the residual of the model or error b.
Symbology used to calculate the sum of squares
The classification variables in the previously constructed model are groups, repetitions, and treatments, identified with i, j, k; their levels are g, r, t/g, respectively. In the present study, g= and both will be equivalent to s, the latter used by Gomez and Gomez (1984). The treatments are divided into g groups and the total observations are calculated as:
Thus, in Gomez and Gomez (1984), there is no grt= 3(3)(45)= 405 pieces of data, but rt= 3(45) = 135 observations.
To simplify manual calculations and to standardize both methodologies, in some denominators of the formulas shown in the results section, g will be considered null, as suggested González et al. (2023) when they applied subsampling within plots in single-factor trials in the completely randomized, randomized complete block, and Latin square experimental designs. In these formulas, the formal symbology described in Mendenhall (1987); Sahagún (2007); Montgomery (2009), among others, was applied.
Software used
InfoStat is used to describe the procedure that will allow the application of the least squares technique to obtain the analyses of variance, but InfoGen (https://www.Info-Gen.com.ar) or SAS (https://www.sas.com), among others, could also be used. To calculate quadratic forms, it is suggested to use the matrix calculator freely available at https://www.matrixcalc.org/es/. The three statistical packages could be used to generate the comparison of treatment means within groups with Tukey’s test or honest least significant difference, and for validation, OPSTAT (http://14.139.232.166/opstat/default.asp) should be applied (Sheoran et al., 1998).
Results
The alternative formulas that will generate the sums of squares (SS) of the analyses of variance that were published in Gomez and Gomez (1984); Shikari et al. (2015); Maranna et al. (2021) are presented below:
In these formulas,
is equivalent to the correction factor used to adjust the sums of squares when least squares are applied; Y is a scalar made up of 135 rows and one column, Y’ is its transposed matrix made up of one row and 135 columns, J is a symmetrical matrix made up of 1s, built with 135 rows and 135 columns. Data can be taken from Gomez and Gomez (1984) to verify the validity of these and of the other formulas shown below.
Error a will be defined from: SS treat 1= SS groups + SS repetitions + SS error a. Thus: SS error a = SS Treat 1- SS groups- SS repetitions. Where:
In Gomez and Gomez (1984), the denominator of the first part of the previous formula was expressed as
, equivalent to
To verify:
To calculate the first component of the above formula, a table with two classification criteria must be constructed: the groups, identified by the subscript i, will be placed in the rows, and the repetitions, represented by the subscript j, in the columns. In this, there will be ij=gr= 3(3) = 9 pieces of data, which implies adding over the subscript k, corresponding to each of the subsets of treatments that are being evaluated; the remaining three components must be calculated in advance. The subscript j, used to represent repetitions, should not be confused with the matrix of ones, identified as J; Y as a variable must also be differentiated from Y as a matrix.
The SS of each subset of treatments in each group is calculated as:
In these, the sum is restricted to over k, and only 15 pieces of data are used, both in the matrix Y, and in its transposed, Y’ (15 rows, one column, and one row, 15 columns, respectively); in addition, the matrix J is formed by 1s, arranged in 15 rows and 15 columns. The order of entering is the same as in Gómez and Gómez (1984), and what is subtracted is a modified correction factor, generated with the sum of
treatments in r repetitions, keeping each of the g groups (G1, G2, G3 or 1, 2, 3) fixed.
If: SS total = SS groups + SS repetitions + SS error a + [SS TREAT (G1) + SS TREAT (G2) + SS TREAT (G3)] + SS error b. So: SS error b= SS total - (SS groups + SS repetitions + SS error a) - [SS TREAT (G1) + SS TREAT (G2) + SS TREAT (G3)]. But as:
So, to verify:
If the experimental area is divided into main unit (MU) and subunit (SU) and additionally, it is defined that the SS total= SS MU + SS SU, it was also observed that the following expression is valid: SS MU= SS Treat 1= SS groups + SS repetitions + SS error a. Thus:
Also, by difference: SS SU= SS total-SS MU. Where:
Using InfoStat or InfoGen
The labels for the columns will be Groups, Repetitions, Treatments, and response variable, identified with G, R, T, Y, respectively, but to avoid confusion with Y, used to define the matrix previously described, another letter could be used, such as X. The 135 records will be entered in three groups, each with 15 varieties, in three repetitions, in the same order as shown in Gomez and Gomez (1984).
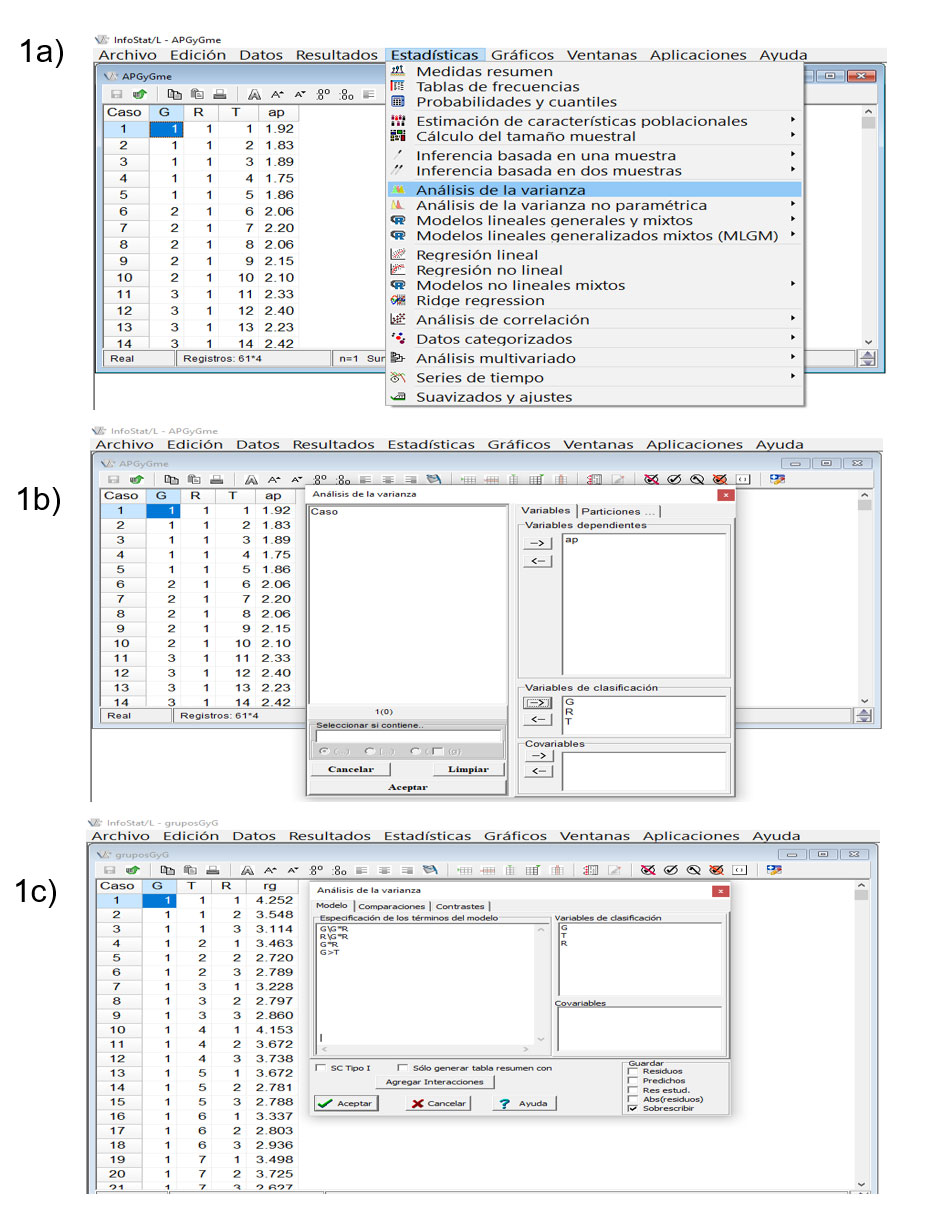
Some fictitious data on plant height (ap; m) from four groups of corn varieties (Zea mays L.) were entered just to show the procedure to be applied in this software (Balzarini et al., 2008; Di Rienzo et al., 2008; Balzarini and Di Rienzo, 2016). The statistical analysis will be generated in two stages: it will be shown how to obtain a general analysis of variance for the partitioning of effects into groups, repetitions, error a, treatments within groups and error b or residual of the model.
The correct F-tests for groups and repetitions should use the mean square of error a, and varieties within each group, that of error b (Figure 1 a, b, c ); in the second stage, it will be indicated how to generate an individual analysis of variance, considering the subdivision of effects by groups of treatments, by default, repetitions and treatments nested within groups are tested against the residual of the model.
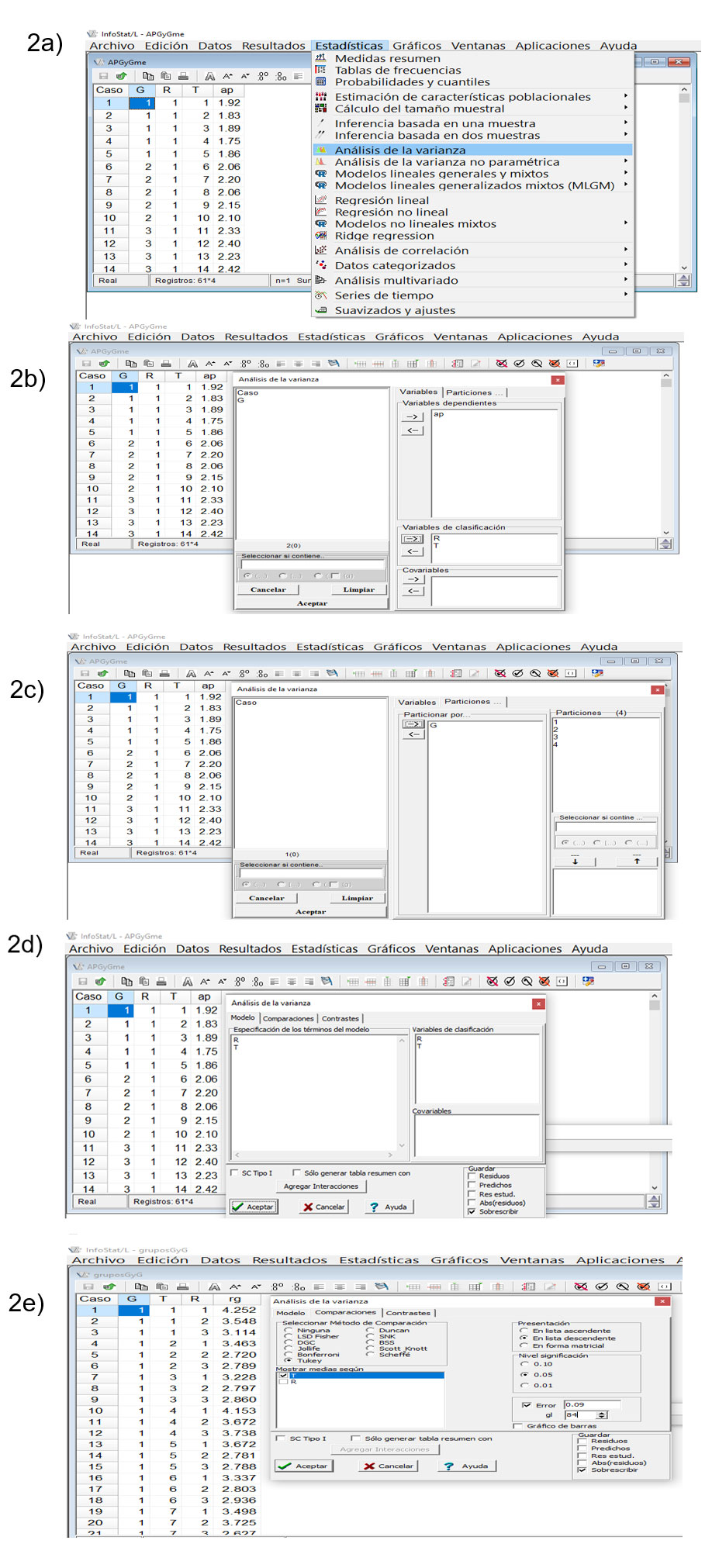
Nevertheless, its F-values are not correct due to the fact that the degrees of freedom and the mean square of the error b shown in the first stage Anova must be used. Both values will need to be manually entered in the dialog box that InfoStat will display (Figure 2 a, b, c, d. e ). Thus, the following was observed:
Note: in the image above, only three groups should be shown, which are the ones that correspond to the data from Gomez and Gomez (1984); four groups were observed because fictitious corn data were entered to show the procedure in InfoStat.
Discussion
The analysis of contrasting groups for subsets of treatments with similarities within each of these is of great relevance in agronomic research. This grouping could be done considering differences in plant height, biological cycle, grain yield, or other important quantitative characteristic, as suggested by Gomez and Gomez (1984); Shikari et al. (2015); Maranna et al. (2021), among others. It could also be classified for cultivars within each subset by geographic or genetic origin, as done by González et al. (2008); González et al. (2011) but without balanced complete block arrangement.
The importance of such studies was also highlighted by Shikari et al. (2015) when, in India, they evaluated 30 cultivars belonging to three Brassica species nested in three treatment groups, each with 10 genetically contrasting materials; they analyzed seed yield and its yield components in a balanced complete block arrangement in a randomized complete block experimental design, hereinafter referred to as BCBA-RCBD. For all variables, highly significant differences were detected between groups; among treatments within groups, there were also differences in most of them, represented by the Gobhi, Yellow and Brown types. Gobhi materials had the highest number of days to maturity, but those with the highest grain yields per hectare were those from the Brown group.
The various statistical methodologies used by Maranna et al. (2021) in which they comprehensively analyzed the data from a BCBA-RCBD. In India, they evaluated 68 advanced lines and seven of the best control cultivars considering their grain yield and yield components in soybeans [Glycine max (L.) Merril]; their main objective was to identify high-yielding genetic material with greater phenotypic stability. Three treatment groups were formed with 25 materials each using three repetitions and considering days to maturity.
Between and within groups, wide genetic variability was observed in 12 agronomic variables. For the northwestern plain of India, it was concluded that the material identified as NRC128 was stable and outperformed the best control (PS 1347) by just over 20%. Due to this and other favorable characteristics that NCR128 had, it was released and recommended for commercial sowing.
The evaluation by González et al. (2008); González et al. (2011) of corn varieties and hybrids from various companies and contrasting regions that are recommended for commercial sowing in the Toluca-Atlacomulco Valley, in the center of the state of Mexico, Mexico. In these studies, an RCBD without BCBA was applied to identify outstanding genetic material within each of the four races found in this Mexican region.
With the proposal made by Gomez and Gomez (1984); Shikari et al. (2015); Maranna et al. (2021), the statistical hypotheses for the subsets of treatments are tested more precisely compared to that made by González et al. (2008, 2011) or other researchers who used an RCBD without BCBA because the environmental heterogeneity that exists in the experimental area when a BCBA is used is fractionated into two components: error a and error b. The former is used to test hypotheses related to effects and variances for treatment groups and for repetitions, while error b is used to detect significant differences between treatments nested within groups.
In the previous context, error a represents the interaction of groups x repetitions, and error b is the residual of the linear model that was constructed and described in the present study. It could also be defined that error a is related to the main unit and error b is associated with the subunit. In González et al. (2008, 2010, 2011) or in multiple trials where yield trials are evaluated to assess the effects between treatments with another option, such as without or with the use of mutually orthogonal contrasts, these are tested with the model residual, which is equivalent to its experimental error; the F-tests for treatments depend on whether or not there are statistical differences between groups of materials in a BCBA.
The sum and point notations have been very useful for representing and analyzing data on quantitative variables in multiple agronomic trials, but as shown by Gomez and Gomez (1984); Martínez (1988); Cochran and Cox (2004), among others, these could be expressed algebraically or matrixically using any symbology when performing manual calculations. In contrast, Mendenhall (1987); Zamudio and Alvarado (1996); Sahagún (1998); Montgomery (2009); Restrepo (2007a, 2007b), among others, use formal symbology to avoid confusion in the description of these procedures, particularly when describing the guidelines for the construction of fixed, random, or mixed models or when applying the rules to obtain the variances of interest from the mathematical expectation of the mean squares.
In addition to the symbology used, other aspects that cause confusion during calculations or in the handling of a statistical package are the absence of the linear model that was applied, as well as the type of effects that are being evaluated, especially in complex factorial experiments; manual calculations are often considered a prerequisite for software application.
In the previous context, in the present study, the statistical model was standardized with the application of two methodologies to calculate degrees of freedom and sums of squares as a prerequisite to achieve the previously mentioned; InfoGen, InfoStat or SAS, among others, will be very useful to achieve this goal.
If the experimental area, as presented by Gomez and Gomez (1984), corresponding to a BCBA-RCBD, is divided into main unit (MU) and subunit (SU), their degrees of freedom would be calculated as rg -1 and r(t - g), respectively, the sum of which gives rise to the rt-1 degrees of freedom of the total, both in this arrangement and in an RCBD without BCBA. In addition, the total for degrees of freedom of treatments within groups would be
which is equivalent to t - g. Thus, it would also be easier to calculate the degrees of freedom for error b as (r-1)(t-g), with r, t, g, being the levels for repetitions, treatments, and groups, respectively.
The results by González et al. (2019) also fractionated the effects between treatments in groups of genetic materials evaluated in an RCBD but without BCBA, these effects were analyzed by means of the technique of mutually orthogonal contrasts, but the precision with which the statistical hypotheses of interest are tested is more reliable when using a BCBA-RCBD because errors a and b are used, although the latter also depend on the magnitude of their degrees of freedom and the existence of significant differences between subsets of treatments.
In an RCBD without BCBA, the sum of squares (SS) of treatments equals SS of groups + SS of treatments within groups. Also, the SS of the experimental error is equal to the addition of the SS of errors a and b, which are obtained when the Anova is generated by combining the data from the g groups. Finally, the SS of repetitions is equal to the difference between the SS of repetitions within each group and the SS of error a. In the above context, as indicated above, error a represents the interaction between groups and repetitions, associated with the main unit, and error b is the residual of the statistical model (εijk) shown in the materials and methods section.
Since several manual calculations must be verified before any statistical package is applied, it should be checked that the addition of the SS of the error in each of the g groups plus the one corresponding to the SS of the error a is equal to the SS of the experimental error in the output that originates by applying an RCBD without BCBA. In relation to the above, the outputs generated by InfoStat, InfoGen or SAS, among others, will be very useful to verify the calculations that will be originated when the previously presented formulas are used.
Authors such as Mendenhall (1987); Sahagún (1998); Montgomery (2009) pointed out the fact that the analysis of variance is an important part of facing the problem represented by the design and analysis of any experimental trial, in which the calculation of degrees of freedom, sums of squares and the construction of appropriate statistical tests considering the relationship between mean squares and their mathematical expectations are involved, especially when considering random or mixed models in more complex situations. This problem has also been highlighted by other researchers, such as Montgomery (2009); Restrepo (2007a, 2007b); Piepho et al. (2003).
The research by González et al. (2023) emphasized correctly entering the instructions or procedures in the specification in the terms of the model in InfoStat or InfoGen or in the SAS editor, to adequately test the statistical hypotheses related to the experiments conducted, without and with subsampling within the experimental units, when the completely randomized, randomized complete block and Latin square experimental designs are applied; Zamudio and Alvarado (1996) made the same recommendation when they developed several codes for SAS to analyze the three previously mentioned experimental designs in balanced subsampling.
In the present study, as done by Gomez and Gomez (1984); Shikari et al. (2015); Maranna et al. (2021), error a should be used to test effects between groups and between repetitions, and error b should be used to perform the same with the subsets of treatments nested within groups (results figures 4 to 8).
For the comparison of means of varieties within groups, InfoStat and InfoGen are very flexible because in both, the database is automatically ordered (last figure of results) and additionally, they allow the correction that must be made to the honest least significant difference or Tukey’s test by performing the manual entering of the degrees of freedom and the mean square of the error b, generated with all the data recorded in the experiment. If the differences between treatment groups are not significant, InfoStat can generate an analysis of variance and comparison of means with Tukey’s test using the same database as when using an RCBA-RCBD. Their validation could be carried out with the Opstat software, available free of charge on its website, in which only the arithmetic means of each variety within each group, as well as the degrees of freedom and the mean square of the error b are entered, which can be generated with any software or, more easily, with the Microsoft Excel spreadsheet.
Conclusions
The appropriate statistical model was constructed considering that the treatments are nested within groups and that the latter are crossed with repetitions. The manual calculation of degrees of freedom and sums of squares was simplified by dividing the experimental area into main unit and subunit, both of which contain errors a and b, respectively, the first represents the interaction of groups x repetitions, and the second is the residual of the statistical model under consideration.
Least squares and quadratic or matrix form techniques generate similar results, but the former is easier to use when applying a statistical package, especially if the number of variables to be analyzed tends to increase. InfoStat is very flexible when applying Tukey’s test to treatments nested within groups because it allows the correction of the honest least significant difference when manually entering the degrees of freedom and the mean square of the error b. If the treatment groups are statistically equal, the trial can be analyzed as an RCBD using the same database as a BCBA-RCBD; as an option to generate the same results, the OPSTAT software can be used, which is available free of charge on its website.
Bibliografía
Balzarini, M. G. y Di Rienzo, J. A. 2016. InfoGen. FCA. Universidad Nacional de Córdoba, Argentina. http://www.info-Gen.com.ar. [ Links ]
Balzarini, M. G.; González, L.; Tablada, M.; Casanoves, F.; Di Rienzo, J. A. y Robledo, C. W. 2008. Manual del usuario de InfoStat. Ed. Brujas, Córdoba, Argentina. 348 p. [ Links ]
Cochran, W. G. y Cox, G. M. 2004. Diseños experimentales. Ed. Trillas SA de CV, 6ta. Reimpresión. México, DF. 661 p. [ Links ]
Di Rienzo, J. A.; Casanoves, F.; Balzarini, M. G.; González, L.; Tablada, M. y Robledo, C. W. 2008. InfoStat, versión 2008. Grupo InfoStat , FCA. Universidad Nacional de Córdoba, Argentina. (https://www.infostat.com.ar). [ Links ]
Gomez, K. A. y Gomez, A. A. 1984. Statistical procedures for agricultural research. 2nd Ed. John Wiley & Sons, Inc. Printed in Singapore. 680 p. [ Links ]
González, H. A.; Vázquez, G. L. M.; Sahagún, C. J. y Rodríguez, P. J. E. 2008. Diversidad fenotípica de variedades e híbridos de maíz en el Valle Toluca-Atlacomulco, México. Revista Fitotecnia Mexicana. 31(1):67-76. [ Links ]
González, H. A.; Pérez, D. J.; Sahagún, C. J.; Franco, M. O.; Morales, E. J.; Rubí, A. M.; Gutiérrez, R. F.; Balbuena, A. 2010. Aplicación y comparación de métodos univariados para evaluar la estabilidad en maíces del Valle Toluca-Atlacomulco, México. Revista Agronomía Costarricense. 34(2):129-143. [ Links ]
González, H. A.; Pérez, L. D. J.; Franco, M. O.; Nava, B. E. B.; Gutiérrez, R. F.; Rubí, A. M. y Castañeda, V. A. 2011. Análisis multivariado aplicado al estudio de las interrelaciones entre cultivares de maíz y variables agronómicas. Revista Ciencias Agrícolas Informa. 20(2):58-65. [ Links ]
González, H. A.; Pérez, L. D. J.; Rubí, A. M.; Gutiérrez, R. F.; Franco, M. J. R. P. y Padilla, L. A. 2019. InfoStat, InfoGen y SAS para contrastes mutuamente ortogonales en experimentos en bloques completos al azar en parcelas subdivididas. Revista Mexicana de Ciencias Agrícolas. 10(6):1417-1431. [ Links ]
González, H. A.; Pérez, L. D. J.; Balbuena, M. A.; Franco, M. J. R.; Gutiérrez, R. F. y Rodríguez, G. J. A. 2023. Submuestreo balanceado en experimentos monofactoriales usando InfoStat y InfoGen : validación con SAS. Revista Mexicana de Ciencias Agrícolas . 14(2):235-249. [ Links ]
Little, T. M. y Hills, F. J. 2008. Métodos estadísticos para la Investigación en la agricultura. Ed.Trillas, SA. de CV. México, DF. 270 p. ISBN:978-968-24-3629-1. [ Links ]
Maranna, S.; Nataraj, V.; Kumawat, G.; Chandra, S.; Rajesh, V.; Ramteko, R.; Manohar Patel, R.; Ratnaparkhe, M. B.; Husain, S. M.; Gupta, S. and Khandekar, N. 2021. Breeding for higher yield, early maturity, wider adaptability and wáterlogging tolerance in soybean (Glycine max L.): a case study. Scientific Reports. 11:22853-https://doi.org/10.1038/s41598-021-02064-x. [ Links ]
Martínez, G. A. 1988. Diseños experimentales. métodos y elementos de teoría . Editorial. Trillas, 1ra . Ed. México, DF. 756 p. [ Links ]
Mendenhall, W. 1987. Introducción a la probabilidad y la estadística. Grupo Editorial Iberoamérica. 1ra . Ed. México, DF. 626 p. [ Links ]
Montgomery, D. C. 2009. Design and analysis of experiments. 7th Ed. John Wiley ( Sons, Inc. USA. 656 p. [ Links ]
Piepho, H. P.; Büsche, A. and Enrich, K. 2003. A Hitchhiker’s guide to mixed models for randomized experiments. J. Agron. Crop Sci. 189(2):310-322. [ Links ]
Restrepo, L. F. 2007 a. Diagramas de estructuras en el análisis de varianza. Revista Colombiana de Ciencias Pecuarias. 20(2):202-208. [ Links ]
Restrepo, B. L. F. 2007 b. La esperanza del cuadrado medio. Revista Colombiana de Ciencias Pecuarias . 20(2):193-201. [ Links ]
Sahagún, C. J. 1998. Construcción y análisis de los modelos fijos, aleatorios y mixtos. Departamento de Fitotecnia. Programa Nacional de Investigación en Olericultura. Universidad Autónoma Chapingo (UACH). Boletín técnico núm. 2, 64 p. [ Links ]
Sahagún, C. J. 2007. Estadística descriptiva y probabilidad: Una perspectiva biológica. 2da. Ed. Universidad Autónoma Chapingo (UACH). México, DF. 282 pp. ISBN: 978 -968-02- 0357-4. [ Links ]
Sheoran, O. P.; Tonk, D. S.; Kaushik, L. S.; Hasija, R. C. and Pannu, R. S. 1998. Statistical Software package for Agricultural research workers. Recent Advances in Information Theory, Statistical ( Computer Applications by D.S. Hooda ( R. C. Hasija Department of Mathematics Statistics, CCS HAU, Hisar. 139-143 pp. [ Links ]
Shikari, A. B.; Pourray, G. A.; Sofi, N. R.; Hussain, A.; Dar, Z. A. and Iqbal, A. M. 2015. Group balanced block design for comparisons among oilseed Brassicae. Academic Journals. 10(8):302-305. https://doi.org/10.5897/SRE2014.5792. [ Links ]
Zamudio, S. F. J. y Alvarado, S. A. A. 1996. Análisis de diseños experimentales con igual número de submuestras. División de Ciencias Forestales. Universidad Autónoma Chapingo (UACH). Primera Edición. México, DF. 85 p. ISBN: 968 884 489 6. [ Links ]
Received: January 01, 2024; Accepted: February 01, 2024











 text in
text in