Services on Demand
Journal
Article
Indicators
Related links
Share
EconoQuantum
On-line version ISSN 2007-9869Print version ISSN 1870-6622
EconoQuantum vol.9 n.2 Zapopan Jul./Dec. 2012
Artículos
La hipótesis de convergencia en América Latina: Un análisis de cointegración en panel*
Domingo Rodríguez Benavides,1 Ignacio Perrotini Hernández,2 Francisco Venegas-Martínez3
1 Departamento de Administración, UAM-Azcapotzalco, e-mail: domr@economia.unam.mx
2 División de Estudios de Posgrado de la Facultad de Economía, UNAM, e-mail: iph@unam.mx
3 Escuela Superior de Economía, IPN, e-mail: fvenegas1111@yahoo.com.mx
Recepción: 30/11/2011
Aceptación: 13/01/2012
Resumen
Este trabajo examina la hipótesis de la convergencia hacia la economía de Estados Unidos para una muestra de 17 países de América Latina, empleando pruebas de raíces unitarias y de cointegración en panel para el periodo 1970-2010. Las pruebas de raíces unitarias en panel aplicadas a la versión restricta de la prueba no son concluyentes en principio con respecto a la hipótesis de la convergencia para esta muestra de países, sin embargo, se muestra que, excluyendo los resultados de las pruebas de Levin y Lin (1992 y 1993), se fortalece la evidencia en contra de la hipótesis de la convergencia absoluta. Aunque la mayoría de las pruebas de cointegración en panel sugieren que los ingresos per cápita de las distintas economías consideradas mantienen una relación de equilibrio estable y de largo plazo con el ingreso per cápita de Estados Unidos, la economía líder. Las estimaciones efectuadas con los métodos de Mark y Sul (2003) y de Kao y Chiang (2000) de la versión irrestricta en panel del modelo indican que el parámetro estimado se encuentra por debajo de la unidad. De acuerdo con los resultados encontrados, no hay evidencia que soporte la hipótesis de la convergencia absoluta para la muestra de estudio de países de América Latina, validando de esta manera la idea de la convergencia condicional.
Palabras clave: modelos econométricos, crecimiento económico, economías latinoamericanas.
Clasificación JEL: C13, F44, C54.
Abstract
This paper examines the hypothesis of convergence to the U.S. economy for a sample of 17 Latin American countries by using unit root tests and panel cointegration for the period 1970-2010. The unit root tests applied to the panel restricted version of the test is inconclusive with respect to the convergence hypothesis for this sample of countries. Although most of the panel cointegration tests suggest that income per capita of the considered economies have a relationship of stable equilibrium and long-term per capita income of the United States, the leading economy. Estimates made with the methods of Mark and Sul (2003) and Kao and Chiang (2000) of the unrestricted version of the panel model indicate that the estimated parameter is below the unit. According to the obtained results, no evidence supports the absolute convergence hypothesis for the studied sample of countries in Latin America, thus validating the idea of conditional convergence.
Introducción
Una cuestión relevante en la literatura empírica sobre el crecimiento económico es si los países pobres tienden a crecer más rápidamente que los países ricos; véase Romer (2002) al respecto. Los fundamentos teóricos de tal aseveración se remiten al modelo de Solow (1956), el cual establece al menos tres razones que podrían justificar dicha convergencia. En primer lugar, el modelo de Solow predice que los países convergen hacia una senda de crecimiento sostenido. En este sentido es lógico pensar que en algún momento, "en el largo plazo", los países más pobres alcanzarán a los más ricos. En segundo lugar, el modelo de Solow implica que la tasa de rendimiento del capital es menor en aquellos países que disponen de un mayor capital por trabajador. De cumplirse lo anterior, existiría un incentivo para que el capital de los países más ricos se desplace hacia los países más pobres. En tercer lugar, si la difusión de los nuevos conocimientos tecnológicos es desigual, es posible que las diferencias internacionales en los niveles de ingreso se deban a que algunos países no se encuentran explotando las mejores técnicas disponibles; tales diferencias se reducirían en la medida que los países más pobres vayan teniendo acceso a las innovaciones tecnológicas.
Con respecto de la convergencia del ingreso per cápita entre las economías, las brechas observadas en esta variable entre países cuestionan seriamente la validez las implicaciones del modelo de Solow. En respuesta al fracaso de la hipótesis de convergencia, surgió en defensa del modelo de Solow la hipótesis de convergencia condicional. Según esta hipótesis, la convergencia depende de que las economías posean ciertos parámetros similares, como tasas de ahorro, depreciación del capital y de crecimiento de la población. De acuerdo con la hipótesis de convergencia condicional, un país pobre sólo puede alcanzar un cierto nivel del país rico debido a las diferencias en la productividad, la tasa de ahorro-inversión y el crecimiento poblacional; véase Cermeño y LLamosas (2007). De esta forma, la posibilidad de convergencia condicional opaca la bondad de predicción del modelo neoclásico y pone en evidencia lo que algunos identifican como un hecho consustancial a la economía mundial moderna: el crecimiento diferencial.
Breve revisión de la Literatura Empírica
Especificación de la pruebas de convergencia absoluta y condicional Uno de los conceptos de convergencia comúnmente empleados es el de β-convergencia. Se dice que existe β -convergencia entre países o regiones si existe una relación negativa entre la tasa de crecimiento del ingreso per cápita y el valor inicial del ingreso per cápita. Lo cual implica que los países más pobres crecen a un ritmo más acelerado que los países ricos. En la década de los noventa, diversos estudios se enfocaron sobre la relación entre la tasa de crecimiento del ingreso per cápita y diferentes medidas de estándares de vida en secciones cruzadas para investigar el proceso de crecimiento. Esos estudios se enfocaron sobre un modelo de la forma:

donde g¡ es la tasa de crecimiento a nivel de país, y¡0 es el valor de la variable a nivel de país en el comienzo del periodo de análisis, X¡ incluye variables por país para controlar efectos específicos de cada uno de ellos y e¡ es el término de perturbación. El valor inicial de la variable, y,o, se incluye con la finalidad de probar la hipótesis de convergencia (Durlauf, 2000). De esta forma, si el valor de β resulta negativo en (1), entonces existe β -convergencia. En términos de la ecuación (1), una forma de probar la versión absoluta, o incondicional, de la convergencia consiste en excluir las variables de control específicas de cada país y verificar que el signo de β en (1) sea negativo; mientras que una prueba de convergencia condicional se lleva a cabo incorporando las variables de control (Barro y Sala-i Martin, 2004). Sin embargo, distintos estudios critican esta forma de probar convergencia. Por ejemplo, Bernard y Durlauf (1996) afirman que una vez que este análisis se aplica a un conjunto de datos de países a través de un modelo correctamente especificado con múltiples estados estacionarios, entonces un coeficiente β negativo para toda la muestra puede atribuirse a una sub-muestra de esos países que converjan al grupo específico de estados estacionarios. Adicionalmente, Quah (1993, 1996b) sugiere que estas pruebas sobre la hipótesis de convergencia sufren de la falacia de Galton, es decir, que una vez que las tasas de crecimiento son regresadas sobre los niveles iniciales, un coeficiente β negativo se debe a una reversión hacia la media, lo cual no necesariamente implica convergencia.
La gran mayoría de estudios que han utilizado (1) han tendido a ignorar los patrones subyacentes de heterogeneidad en los datos al utilizar un modelo de regresión idéntico para todos los países en la muestra. Algunos de ellos usan variables dummy para América Latina o para el África Subsahariana con el fin de controlar las diferencias en el proceso de crecimiento para esos grupos de países; sin embargo, esto no es suficiente para capturar los estadísticos de los grupos en el conjunto de datos. Al respecto, Bernard y Durlauf (1994 y 1995) evalúan la posibilidad de convergencia utilizando el siguiente modelo:

donde y¡t, es el ingreso por persona del país a estudiar, yjt el ingreso por persona del país líder o de referencia, α¡j es una constante que denota diferencias permanentes entre las dos economías (Cermeño y LLamosas, 2007). Si hay convergencia, las diferencias entre dos países tenderán a reducirse a través del tiempo, es decir, se requiere que α¡j = 0 para que las diferencias se hayan eliminado por completo (convergencia absoluta). De no cumplirse lo anterior, se tenderá a un determinado nivel diferenciado (convergencia condicional). De esta manera, el cumplimiento de la hipótesis de convergencia absoluta requiere que β = 1 y α¡j = 0. Si α¡j≠ 0 entonces hay evidencia de convergencia condicional.
Si se cumple la convergencia absoluta, entonces una forma sencilla y directa de probarla sería obtener la diferencia entre el ingreso por persona del país a estudiar y el ingreso por persona del país líder o de referencia, ambos en logaritmos naturales:

A partir de esta serie, la hipótesis nula de no-convergencia se puede formular como:
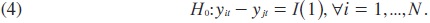
Lo anterior se puede llevar a cabo a través de las pruebas de raíces unitarias. A esta versión de la prueba se le conoce como la versión restricta. De acuerdo con Cheung y García (2004), el probar la hipótesis nula establecida en (4) puede sesgar los resultados hacia la aceptación de la hipótesis de no convergencia debido al reducido poder de las pruebas de raíces unitarias, por lo que ellos proponen evaluar la hipótesis de convergencia a través de la siguiente manera:
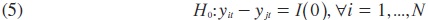
Si no es posible rechazar (4) y (5) al mismo tiempo, los datos no pueden proveer evidencia para aceptar o rechazar la hipótesis de convergencia.
Por lo que respecta a la versión irrestricta de la prueba, ésta no se supone a priori y se emplea el modelo (2) para estimar los parámetros α¡j y β. Bajo esta versión de la prueba, la hipótesis de no convergencia se evalúa aplicando la prueba de raíz unitaria sobre los errores estimados en este modelo. Bajo este enfoque, la hipótesis nula establece que no hay cointegración entre los ingresos por persona del país de interés con respecto de la economía líder. Además, esta versión de la prueba tiene la ventaja de que es posible determinar si la constante es significativa y, por lo tanto, puede mostrar evidencia de convergencia condicional, así como verificar si el vector (1,-1) del modelo restricto se cumple o no.
La prueba planteada en (3) para probar la hipótesis de convergencia entre dos países se puede extender para un modelo panel que comprenda un conjunto de países de la siguiente forma:

donde y¡t, es el ingreso per cápita del país i en el momento t, y y¡t, es el ingreso per cápita del país líder en el tiempo t, ambos en logaritmos. En consecuencia, la hipótesis de convergencia entre dos economías se puede probar por medio del análisis de integración y cointegración en panel cuando los ingresos por habitante de ambos países no son estacionarios (Díaz et al, 2009), lo cual se puede llevar a cabo aplicando distintas pruebas de raíces unitarias en panel al conjunto de series resultante de (5).
Una versión menos restrictiva de (6) es la extensión de (2) al modelo panel de la siguiente forma:
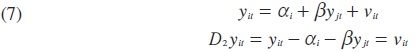
De esta manera, el modelo (7) provee una estimación de la pendiente para el panel en conjunto, lo cual permite probar la hipótesis de convergencia para el conjunto de países incorporados en el panel. De acuerdo con el método de estimación de Mark y Sul (2003) para paneles cointegrados, no sólo es posible estimar el parámetro β para el panel en conjunto, sino también un parámetro para cada una de las unidades consideradas, lo cual permite capturar una mayor heterogeneidad, por lo que (7) se puede escribir del siguiente modo:
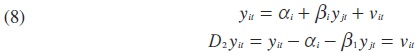
En este trabajo se utilizarán las versiones de la prueba establecidas en (6), (7) y (8) con técnicas de cointegración en panel con la finalidad de probar la hipótesis de la convergencia para una muestra de 17 países de América Latina con respecto a la economía líder que, en este caso, es la economía de Estados Unidos.
La literatura empírica sobre el tema
Evans (1997) demuestra que cuando se incorporan variables de control en la ecuación (1), a pesar de que éstas controlan el 90% de la varianza de los niveles de PIB per cápita en el estado estacionario, el límite de probabilidad del estimador de mínimos cuadrados del coeficiente en el ingreso inicial (que es el indicador de convergencia) es aproximadamente igual a la mitad de su verdadero valor; por esta razón no es conveniente realizar inferencias empleando este tipo de regresiones.
Dentro de los estudios que han empleado técnicas de series de tiempo destacan Linden (2000) quien estudia el conjunto de países de la OECD aplicando las pruebas de raíces unitarias ADF y KPSS por pares, encontrando convergencia sólo para Noruega, Suecia y Reino Unido, de acuerdo a dichas pruebas. Por otra parte, Amable y Juillard (2000), aplicando las mismas pruebas en una muestra de 53 países, encontraron que la prueba ADF casi nunca aceptó convergencia, con excepción de Dinamarca y Alemania.
Asimismo, Camarero, Flores y Tamarit (2002) al estudiar los países que conforman el Mercosur, a través de las pruebas ADF por pares y de modelos panel, encuentran evidencia de convergencia en determinados países. Por su parte, Easterly, Fiess y Le-derman (2003) analizan la hipótesis de la convergencia entre México y Estados Unidos con la prueba de Johansen encontrando evidencia de convergencia condicional. Por último, Cheung y Pascual (2004) analizan el caso del grupo de los siete (G-7) por medio de las pruebas ADF por pares y de estudios de panel, la evidencia mostrada por ellos es que la prueba ADF por pares no muestra evidencia de convergencia.
Cermeño y LLamosas (2007) emplean tanto la versión restricta como la irrestricta del modelo (2) para probar la hipótesis de convergencia del PIB per cápita de 6 países emergentes con respecto de Estados Unidos. Con tal fin, ellos realizan pruebas de cointegración bajo posible cambio estructural siguiendo el enfoque de Gregory y Hansen (1996). Sus resultados sugieren que en la mayoría de los casos no se encuentra evidencia a favor de convergencia en presencia de cambio estructural y que las brechas de ingreso per cápita de los países considerados con respecto de Estados Unidos son consistentes con procesos de no convergencia.
Dentro de los estudios realizados para probar convergencia a nivel regional destaca el de Díaz, Sánchez y Mendoza (2009), quienes efectúan pruebas de raíces unitarias y de cointegración en panel para probar tal hipótesis a nivel de los estados de la de República Mexicana hacia el PIB del Distrito Federal en el periodo 1970-2004. Ellos encuentran, a través de la estimación de las ecuaciones (6) y (8), evidencia a favor de la convergencia condicional y sus estimaciones de la velocidad de convergencia indican que las regiones más ricas convergen más rápidamente que las pobres.
Metodología econométrica y datos
Pruebas de Raíces Unitarias en Panel
Las pruebas de raíces unitarias en panel comprenden el análogo multivariado a las pruebas de raíces unitarias univariadas estándar, como son las pruebas Dickey-Fuller Aumentada (ADF), Phillips-Perron (PP) y la Kwiatkowski, Phillips, Schmidt y Shin (KPSS). El principal propósito de extender la aplicación de las pruebas de raíces unitarias univariadas a las pruebas de raíces unitarias en panel ha sido el de incrementar el tamaño de la muestra a partir de los datos de sección cruzada para aumentar la potencia de las pruebas.
Por otro lado, diversas pruebas sobre raíces unitarias en panel han sido sugeridas por Levin y Lin (1992 y 1993) (de aquí en adelante LL), Im, Pesaran y Shin (1995, 1997 y 2003), con extensiones y ajustes más recientes por Harris y Tzavalis (1999), Maddala y Wu (1999) y Breitung (2000). Todas estas pruebas consideran como hipótesis nula la no estacionariedad (es decir, la presencia de una raíz unitaria) y prueban contra la alternativa de estacionariedad. Sin embargo, no todas las pruebas propuestas siguen esta convención, ya que una excepción la constituye la prueba de Hadri (2000), que prueba la hipótesis nula de estacionariedad contra la alternativa de una raíz unitaria en el panel de datos.
El enfoque básico para probar la presencia de una raíz unitaria es considerar una versión del siguiente modelo:

En el caso de la prueba de LL se supone que: 1) eit son IID(0,σ2e), es decir, que cada proceso individual para cada i es independiente entre las unidades y que no existe correlación serial y 2) que ρ¡ = ρ para todo i. Este último supuesto impone homogeneidad, ya que se supone que cada proceso individual es el mismo entre todas las unidades de sección cruzada del panel. El primer supuesto asegura que no existe cointegración entre pares o grupos de individuos en las secciones cruzadas. Éste es el principal supuesto, ya que, en muchas situaciones, éste puede ser el caso para el conjunto de variables en cuestión, donde frecuentemente la evidencia empírica muestra que los mercados se encuentran vinculados en términos de relaciones de equilibrio de largo plazo.
La consecuencia de suponer que no existen relaciones de cointegración entre las variables de sección cruzada ha sido explorada por Banerjee, Cockerril y Russell (2001); ellos encuentran que el grupo de pruebas de raíces unitarias en panel considerado por LL tienden a rechazar, frecuentemente, la hipótesis nula de no estacionariedad.
El conjunto de pruebas empleadas para probar la presencia de raíces unitarias en panel son las propuestas por Levin y Lin (1992 y 1993), de aquí en adelante (LL), las cuales cubren un amplio espectro de especificaciones. El conjunto de pruebas propuesto por LL se presentan en el cuadro 1.
A partir del conjunto de pruebas propuestas por LL (1992), la primera y la más simple es cuando se hace z¡t, = 0 en (9), mientras que las pruebas 2-6 cubren un conjunto de alternativas que incorporan diferentes términos deterministas. En todos los casos, la hipótesis nula es H0: ρ = 0 contra la alternativa Hi. ρ < 1. De esta manera, bajo la hipótesis nula todas las i series en el panel contienen una raíz unitaria, mientras la alternativa es que todas las series individuales son estacionarias. Claramente, la hipótesis alternativa impone una restricción muy fuerte. LL muestran que en la medida en que N → ∞ y T → ∞ la distribución subyacente del estadístico t para probar la hipótesis nula se distribuye como una normal estándar N(0,i) (Baltagi, 2001).
Existen varias consideraciones con las pruebas LL (1992) que se deben tener en cuenta en extensiones o alternativas. LL (1993) desarrollan procedimientos de prueba que cuidan la posibilidad de que se encuentren presentes problemas de autocorrelación y heteroscedasticidad en las pruebas LL (1992). El principal modelo comprende:
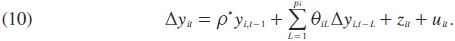
Es decir, la ecuación (9) se transforma en una versión equivalente en primeras diferencias, de tal forma que ahora la hipótesis nula es H0: ρ* = ρ - 1 = 0. De esta manera, la principal diferencia con respecto a las pruebas LL (1992) es que se incorporan diferentes rezagos entre las i secciones cruzadas en el modelo. En esta investigación se aplican tres versiones de la propuesta de LL (1993), las cuales corresponden a los modelos 8, 9 y 10 del cuadro 1.
Todos los modelos presentados en el cuadro 1 se pueden estimar usando OLS a través de un modelo de regresión agrupada. Como se puede ver, la característica más sobresaliente de la prueba LL es el supuesto efectuado sobre coeficiente autorregresivo de primer orden, el cual se supone homogéneo entre las unidades, esto a diferencia de la prueba Im, Pesaran y Shin (1995) que permite que éste sea distinto entre las unidades.
Otro enfoque de las pruebas LL es el relacionado con los métodos empleados para estimar modelos panel con efectos fijos (donde αi > 0). Generalmente, si se permite la heterogeneidad (αi y/o ηi aparecen en el modelo), entonces los estimadores usuales de modelos panel basados sobre el estimador de grupos "within" (tales como el modelo de mínimos cuadrados ordinarios de variables dummy) han mostrado que sufren de una grave pérdida de potencia (Breitung, 2000). De esta forma, Breitung propone una prueba involucrando únicamente una constante en el modelo, es decir, sin efectos fijos, y encuentra que su prueba (UB) tiene sustancialmente mayor potencia y que es mucho más robusta con respecto a la presencia de rezagos en el proceso generador de datos (DGP) que subyace al verdadero modelo que las pruebas LL.
Otra prueba de raíces unitarias en panel es la propuesta por Im, Pesaran y Shin (1995), de aquí en adelante IPS; ésta es una prueba del tipo Dickey-Fuller Aumentada (1981), la cual prueba la hipótesis nula de que la variable de panel tiene una raíz unitaria. Im, Pesaran y Shin (1997) sostienen que el estadístico de prueba utilizado se distribuye como una normal estándar según la hipótesis nula de que todas las series poseen una raíz unitaria. En esta prueba, la hipótesis nula es que las series del panel son integradas de orden 1 (Díaz et al., 2009). El estadístico de prueba de medias grupales en Im, Pesaran y Shin (1997) es:

en el cual

donde T es el número de años, N denota el número de grupos y 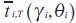 es el estadístico de prueba individual para probar si el proceso poseejaíces unitarias y¡ = 0 frente a la alternativa de estacionariedad conjunta. La media E
es el estadístico de prueba individual para probar si el proceso poseejaíces unitarias y¡ = 0 frente a la alternativa de estacionariedad conjunta. La media E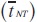 y la varianza var
y la varianza var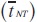 son tabuladas para diferentes tamaños de muestras y estructuras de rezagos para modelos con intercepto y tendencia lineal.
son tabuladas para diferentes tamaños de muestras y estructuras de rezagos para modelos con intercepto y tendencia lineal.
Como se estableció anteriormente, uno de los principales supuestos de la prueba LL es la imposición de la homogeneidad en el parámetro autorregresivo de primer orden, es decir, se supone que ρ¡ = ρ en las ecuaciones (9) y (10). La hipótesis alternativa que se prueba bajo este modelo es que H1: ρ < 1, es decir, que todas las unidades de sección cruzada son estacionarias. Mientras que la prueba IPS (1997) relaja esta restricción de homogeneidad y estima la ecuación (10) con ρ¡, es decir, se permite que dicho parámetro sea distinto entre las series individuales i del panel. Ellos también permiten diferentes rezagos, como en el caso de LL (1993), para cada una de las i secciones cruzadas en el modelo usando el siguiente modelo:
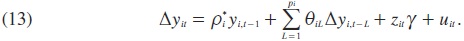
Las hipótesis relevantes son H0: ρ*¡ = 0 para toda i, esto es, que cada serie en el panel contiene una raíz unitaria para toda i y la H1: ρ*¡< 0 para al menos un i, es decir, que al menos una de las series individuales en el panel es estacionaria. El otro aspecto importante del enfoque propuesto por IPS, y que se opone al enfoque de la prueba de Levin y Lin, es que en lugar de agrupar los datos, se realizan las pruebas de raíces unitarias sobre las N series de tiempo que tienen la misma longitud de tiempo T. De esta manera, el estadístico de prueba IPS se estima como un promedio de las pruebas Dickey-Fuller o Dickey-Fuller Aumentada (si las u¡, se encuentran serialmente correlacionadas entre las unidades de sección cruzada). IPS proponen emplear las pruebas LM-barra y t-barra para llevar a cabo la prueba, donde este último viene dado por:

IPS muestran que su estadístico, denotado por IPS_97, para probar la hipótesis nula se encuentra normalmente distribuido. Sin embargo, la prueba IPS adolece de los mismos problemas de las pruebas LL. Dado que cada i es independiente entre las unidades, lo cual implica que no hay correlación, tanto de corto como de largo plazo, entre las unidades y que de esta forma no hay cointegración entre pares o grupos de individuos en esas secciones cruzadas.
Por su parte, la prueba de Harris y Tzavalis (1999), de aquí en adelante HT, sigue el mismo procedimiento propuesto por Dickey y Fuller (1981) y Phillips y Perron (1988) para el caso univariado. HT realizaron experimentos Monte Carlo para analizar las propiedades de las pruebas de LL cuando T, el componente de series de tiempo del conjunto de los datos, es pequeño. En particular, ellos analizan la potencia de las pruebas para rechazar la nula cuando ésta es falsa, y encuentran que el supuesto hecho por las pruebas LL de que T → ∞ resulta en una prueba que pierde potencia (especialmente cuando T es menor a 50). En consecuencia, ellos sugieren realizar la prueba de raíces unitarias en panel suponiendo que T es fijo, debido a que mejora la potencia de la prueba en muestras donde T es pequeño. Al respecto, HT consideran los siguientes tres modelos:
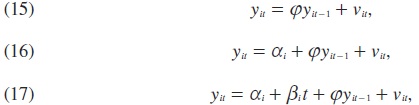
los cuales corresponden a los empleados por Levin y Lin (1993) y requieren, de forma similar a la prueba de LL, que el coeficiente autorregresivo sea homogéneo tanto en la hipótesis nula como en la alternativa, ya que ellos agrupan los datos sobre la dimensión de sección cruzada. En los modelos (15) a (17), denominados HT_1 a HT_3, la hipótesis nula es que una raíz unitaria está presente en el proceso generador de datos (DGP), esto es, φ . Bajo la hipótesis alternativa, se supone |φ| < 1. De acuerdo con Harris y Tzavalis (1999), lo que pueda resultar de cada modelo depende, en parte, sobre lo que se conozca del DGP y, por tanto, de cómo las hipótesis nula y alternativa sean formuladas. El modelo (15) es el caso simple del panel homogéneo. El modelo (16) es un proceso de raíz unitaria con intercepto heterogéneo bajo la hipótesis nula y un proceso estacionario con intercepto heterogéneo bajo la hipótesis alternativa. El modelo (17), el cual incluye tanto efectos fijos heterogéneos como tendencias individuales, provee una prueba con mayor potencia para distinguir entre la hipótesis nula de que cada serie sigue una caminata aleatoria con intercepto y la hipótesis alternativa de que cada serie es estacionaria alrededor de una tendencia determinista, de manera análoga al caso univariado seguido por Phillips y Perron (1988).
Todas las pruebas anteriormente expuestas se basan en el supuesto sobre la hipótesis nula de que las series individuales en el panel son en conjunto no estacionarias, contra la alternativa de que algunas o todas esas series son estacionarias. Por su lado, Hadri (2000) ha propuesto una prueba donde la hipótesis nula establece que las series de tiempo para cada i son estacionarias alrededor de una tendencia determinista contra la hipótesis alternativa de una raíz unitaria en el panel de datos. Para ello, Hadri (2000) provee el siguiente modelo:

donde r¡t, = r¡t-1+ u¡t, y u¡t∼ IID(0,σ2u) . Así r¡t, es una caminata aleatoria y ε¡t, es un proceso estacionario. A través de un proceso de iteración hacia atrás es posible reescri-bir (18) como:

donde 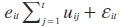 , es la suma acumulada para cada unidad de sección cruzada i de los residuales pasados u¡t. Bajo la hipótesis nula de estacionariedad, la varianza de e¡t, es igual a cero, es decir, los y¡t, no tienen intercepto, pero que en cambio son estacionarios alrededor de un componente determinista en la ecuación (19).
, es la suma acumulada para cada unidad de sección cruzada i de los residuales pasados u¡t. Bajo la hipótesis nula de estacionariedad, la varianza de e¡t, es igual a cero, es decir, los y¡t, no tienen intercepto, pero que en cambio son estacionarios alrededor de un componente determinista en la ecuación (19).
Pruebas de Cointegración en Panel
Kao (1999) y Pedroni (1995, 1999) han propuesto pruebas de cointegración en panel empleando el enfoque uniecuacional donde la hipótesis es que no existe cointegración entre las variables en cuestión. De igual forma, Mckoskey y Kao (1998) han desarrollado una prueba basada en los residuos con el fin de probar la nula de cointegración en lugar de la nula de no cointegración en el panel. Larsson, Lyhagen y Lothgren (2001), bajo un contexto multiecuacional, construyen una prueba de panel para el rango de cointegración en paneles heterogéneos basada sobre la media del estadístico de la traza del rango de los individuos desarrollado por Johansen (1995a).
Pruebas de cointegración de Kao (1999). Las pruebas propuestas por Kao (1999) son pruebas del tipo ADF similares al enfoque estándar uniecuacional adoptadas en el procedimiento de EG de dos pasos. El procedimiento básico consiste en estimar el siguiente modelo de regresión en panel:
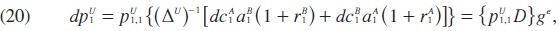
donde se supone que y¡t, y x¡t, son no estacionarios y:

y donde 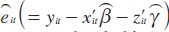 form son los residuos de la ecuación (20) estimada. En este caso se intenta probar la hipótesis nula de no cointegración, H0: ρ = 1, en virtud de (21), contra la alternativa de que y y x están cointegradas, es decir, que H1 : ρ < 1. Kao desarrolló cuatro pruebas tipo Dickey-Fuller (DF), con z¡t en la ecuación (11) limitada al caso de efectos fijos, es decir z¡t= α¡. Dos de las pruebas de Kao suponen fuerte exogeneidad de los regresores y los errores en (20) y se denotan por DFp y DFt, mientras que las otras pruebas, que no son paramétricas, hacen correcciones por alguna relación endógena y se denotan por DF*p y DF*t,. Las cuatro pruebas incluyen correcciones no paramétricas para la posibilidad de que se encuentre presente correlación serial, debido a que la ecuación (21) involucra una regresión de mínimos cuadrados ordinarios (OLS) de
form son los residuos de la ecuación (20) estimada. En este caso se intenta probar la hipótesis nula de no cointegración, H0: ρ = 1, en virtud de (21), contra la alternativa de que y y x están cointegradas, es decir, que H1 : ρ < 1. Kao desarrolló cuatro pruebas tipo Dickey-Fuller (DF), con z¡t en la ecuación (11) limitada al caso de efectos fijos, es decir z¡t= α¡. Dos de las pruebas de Kao suponen fuerte exogeneidad de los regresores y los errores en (20) y se denotan por DFp y DFt, mientras que las otras pruebas, que no son paramétricas, hacen correcciones por alguna relación endógena y se denotan por DF*p y DF*t,. Las cuatro pruebas incluyen correcciones no paramétricas para la posibilidad de que se encuentre presente correlación serial, debido a que la ecuación (21) involucra una regresión de mínimos cuadrados ordinarios (OLS) de 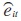 , sobre un solo valor rezagado de
, sobre un solo valor rezagado de 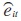 ,. Alternativamente, Kao también propuso una prueba que extiende (21) para que incluya diferencias rezagadas en los residuales, así obtiene una versión ADF de su prueba, y de esta manera una versión que paramétricamente prueba para correlación serial como parte del procedimiento de estimación.
,. Alternativamente, Kao también propuso una prueba que extiende (21) para que incluya diferencias rezagadas en los residuales, así obtiene una versión ADF de su prueba, y de esta manera una versión que paramétricamente prueba para correlación serial como parte del procedimiento de estimación.
Todas las pruebas se distribuyen asintóticamente bajo la distribución normal estándar. Es importante destacar que las cinco versiones de Kao imponen homogeneidad en el coeficiente de la pendiente β , es decir, no se permite que varíe entre los individuos que conforman el panel.
La prueba de cointegración de Kao (1999) se lleva a cabo a través de la estimación de los siguientes estadísticos:

La hipótesis nula tanto en el caso de las pruebas de cointegración en panel de Kao (1999) como las de Pedroni (1995) y (1999) es que la ecuación estimada no está cointegrada.
Pruebas de cointegración de Pedroni (1995, 1999). Por otra parte, las pruebas de Pedroni (1995) y (1999) tienden a relajar el supuesto de homogeneidad impuesto en las pruebas de Kao. Pedroni propone el siguiente modelo:
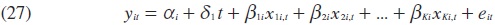
para probar la hipótesis nula de no cointegración sobre los residuales de este modelo a través de un procedimiento similar al descrito en (21), Harris y Sollis (2003). Debido a que se permite que tanto las αi; y las βi varíen entre los i miembros del panel, este enfoque (más flexible) contempla una considerable heterogeneidad tanto de corto como de largo plazo, la cual permite considerar que tanto la dinámica como los efectos fijos pueden diferir entre los individuos en el panel y, por ende que el vector de cointegración puede ser diferente entre ellos bajo la hipótesis alternativa.
La forma en que es incorporada la dinámica para corregir correlación serial depende de la prueba de Pedroni en el modelo considerado. Pedroni construye tres pruebas no paramétricas que intentan corregir correlación serial: i) un estadístico de razón de varianzas no paramétrico; ii) una prueba análoga al estadístico-rho de Phillips-Perron (PP) (1988); y iii) una prueba similar al estadístico t de PP. La prueba de Pedroni (1995) se lleva a cabo para el caso de dos variables a través de los siguientes estadísticos:
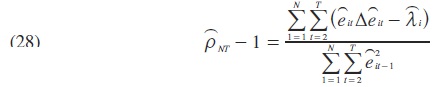
el cual sigue una distribución t de Student, con los siguientes estadísticos:
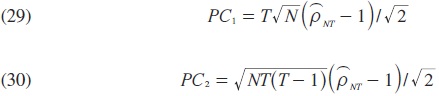
los cuales prueban la hipótesis nula de no cointegración entre las variables en cuestión. Pedroni (1999) ha propuesto siete estadísticos diferentes para probar cointegración en datos en panel, de los cuales cuatro de ellos se basan en un término en común, lo cual se refiere a la dimensión intragrupos (Within), y los últimos tres se basan en la dimensión entre los grupos (Between). Ambos tipos de pruebas se enfocan sobre la hipótesis nula de no cointegración. Sin embargo, la distinción viene de la especificación de la hipótesis alternativa. Para la prueba que se basa en "Within", la hipótesis alternativa es que ρi = ρ < 1 para toda i, mientras que para los últimos tres estadísticos que se basan sobre la dimensión "Between", la hipótesis alternativa es ρi < 1, para toda i. Las distribuciones en muestras finitas para los siete estadísticos han sido tabuladas por Pedroni a través de simulaciones Monte Carlo. El estadístico de prueba calculado debe ser menor al valor crítico tabulado para rechazar la hipótesis nula de la ausencia de cointegración.
Prueba de cointegración de Larsson. Larsson et al. (2001), contrariamente a las pruebas anteriormente planteadas, se basan en el enfoque de Johansen (1988) de máxima verosimilitud, evitando de esta manera el uso de las pruebas de raíces unitarias sobre los residuales del modelo estimado, lo cual permite relajar el supuesto de un solo vector de cointegración y de esta forma probar la presencia de múltiples vectores de cointegración. El modelo que se propone parte del supuesto de que el proceso generador de datos para cada una de las secciones cruzadas puede ser representado por la siguiente especificación del modelo de corrección de error (MCE):
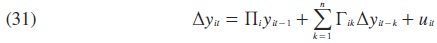
Larsson et al. (2001) proponen la estimación del modelo anterior para cada una de las secciones cruzadas y así calcular el estadístico de la traza, LR¡r, por el método de máxima verosimilitud. De esta manera, el estadístico del rango de la traza en el panel se obtiene como el promedio del estadístico de las trazas de las N secciones cruzadas. Las hipótesis nula y alternativa para esta prueba son, respectivamente:
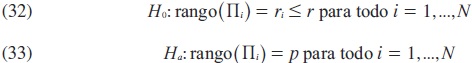
donde p es el número de variables incorporadas en el modelo para probar la posible cointegración entre ellas. El estadístico de prueba del rango de la traza estandarizado, denotado por Ylr , está dado por:
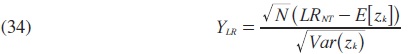
donde LRNT es el promedio del estadístico de la traza para cada unidad de sección cruzada, y E[zk] y Var(zk) son la media y varianza del estadístico asintótico de la traza reportados en Larsson et al. (2001).
Métodos de estimación en panel para variables cointegradas Para los modelos de cointegración en panel, las propiedades asintóticas de los estimadores de los coeficientes de los modelos de regresión y las pruebas estadísticas asociadas son diferentes de los que se estiman por los modelos de cointegración de series de tiempo; véase Baltagi (2008). Algunas de esas diferencias se han puesto de manifiesto en trabajos recientes en Kao y Chiang (2000), Phillips y Moon (1999), Pedroni (2000, 2004) y Mark y Sul (2003), por mencionar unos cuantos. Los modelos de cointegración en panel están diseñados para estudiar cuestiones sobre relaciones de largo plazo típicamente encontradas en datos macroeconómicos y financieros. Tales relaciones de largo plazo son frecuentemente postuladas por la teoría económica o financiera y éste es el principal interés para estimar los coeficientes de regresión y probar si se satisfacen o no las restricciones teóricas. Phillips y Moon (1999) y Pedroni (2000) proponen un estimador modificado (FM), el cual puede ser visto como una generalización del estimador de Phillips y Hansen (1990), mientras que Kao y Chiang (2000) proponen un método alternativo que se basa en el estimador de mínimos cuadrados dinámicos (DOLS), el cual toma como punto de partida los trabajos de Saikkonen (1991) y Stock y Watson (1993). En la presente investigación se emplearán tanto los estimadores propuestos por Kao y Chiang para vectores cointegrantes heterogéneos (FMOLS y PDOLS) como el estimador para vectores cointegrantes homogéneos de Mark y Sul (2003) para estimar la versión irrestricta de la prueba de convergencia con los datos de la muestra de países de América Latina.
Por lo que respecta a los datos empleados en este trabajo, las series del PIB per cápita, tanto de los países de América Latina como de Estados Unidos, provienen de la base de datos del Banco Mundial y todas están expresadas en dólares constantes del 2000.
Los estimadores FMOLS y PDOLS de Kao y Chiang
Kao y Chiang (2000) consideran el siguiente modelo de regresión en panel:

donde las {yit} son de dimensión 1 X 1, β es un vector k X 1 de parámetros de pendientes, zu es el componente determinista, y {uit} son los términos de perturbación estacionarios. Las {xit} son procesos integrados de orden 1, para todo i, donde

A continuación en las ecuaciones dadas en (37) se presentan distintos procedimientos de estimación del vector de los parámetros de interés en paneles de datos para modelos del tipo (35), o sea, homogéneos:
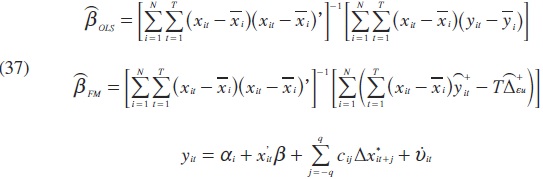
La última expresión de (37) es la ecuación estimada por (DOLS o PDOLS).
Resultados
En primer lugar, se averigua la posible presencia de una raíz unitaria en (6), es decir, en la diferencia del ingreso por habitante de cada economía con respecto al ingreso por habitante de Estados Unidos. Los resultados de las pruebas de raíces unitarias en panel para D1 y¡t, se presentan en el cuadro 2.
En los casos en los que fue necesario incorporar rezagos en las pruebas se incluyó un solo rezago, con y sin tendencia determinista. Los resultados de las pruebas de raíces unitarias aplicados a D1 y¡t son un tanto ambiguos. Aunque del total de las 26 pruebas efectuadas, 16 sugieren que la variable D1 y¡tposee una raíz unitaria, mientras que sólo 10 de las pruebas sugieren estacionariedad para esta variable. Sin embargo, la forma en cómo se especifica cada prueba con respecto a la hipótesis de convergencia en los modelos de crecimiento tiene algunas implicaciones, como lo sugieren Maddala y Wu (1999), específicamente en el caso de las pruebas LL, que asumen homogeneidad en el parámetro autorregresivo; la hipótesis nula (ρ = 0) implicaría que ninguna de las economías bajo estudio converge de tal forma que el parámetro es idéntico para todas ellas, lo cual puede no tener sentido, ya que no hay ninguna razón para que todos los países converjan a la misma tasa, si es que estos últimos convergen. El argumento anterior sugiere que, dado el carácter restrictivo de las pruebas LL, en cuanto que asumen homogeneidad del parámetro autorregresivo bajo la hipótesis nula, pueden no ser las más apropiadas para probar la hipótesis nula de raíz unitaria enD1 y¡t. De hecho, sólo cuatro de las diez pruebas LL revelaron que no hay convergencia absoluta en la muestra de países en cuestión.
Un aspecto importante en las pruebas es el hecho de que cuando la prueba permite la posibilidad de controlar efectos fijos, 7 de las 9 pruebas aplicadas bajo esta especificación sugieren que la variable en cuestión tiene una raíz unitaria. Mientras que cuando la prueba incorpora tanto efectos fijos como efectos de tiempo heterogéneos, los resultados también proveen evidencia mixta. Incluso dentro del mismo conjunto de pruebas se presenta esta ambigüedad, por ejemplo, las pruebas LL_2, LL_3, LL_4, LL_5 sugieren que la variableD1 y¡tposee una raíz unitaria, en tanto que las pruebas LL_1, LL_6, LL_7, LL_8, LL_9 y LL_10 indican que es estacionaria.
Otra cuestión importante a destacar es que las pruebas de raíces unitarias en panel que se han propuesto más recientemente, específicamente las pruebas de IPS_2003 y de Hadri (2000), que incorporan la posibilidad de capturar tanto efectos fijos de manera individual como en combinación con efectos de tiempo heterogéneos, sugieren que dicha serie tiene una raíz unitaria.
Si se excluyen los resultados de las pruebas LL en la prueba de raíces unitarias de D1 y¡t sólo cuatro de las dieciséis pruebas empleadas rechazan la hipótesis de la raíz unitaria. De esta manera, la mayor parte de la evidencia sugiere que la variable D1 y¡t posee una raíz unitaria y, de esta manera, hay una diferencia sustancial entre el logaritmo natural de los ingresos per cápita de cada uno de los países considerados para la muestra de América Latina con respecto del mismo indicador de Estados Unidos.
Dado el anterior resultado, se verificará ahora la versión irrestricta de la prueba de acuerdo a los modelos (7) y (8). Para tal fin, primero se prueba la presencia de una raíz unitaria en panel para y¡,. Los resultados de las pruebas se presentan en el cuadro 3.
A diferencia de los resultados de las pruebas aplicadas a D1 y¡t, 17 de las 26 pruebas de raíces unitarias en panel aplicadas al ingreso per cápita de los países de América Latina, sugieren que dicha variable es estacionaria. En este caso, las únicas pruebas que señalan que la variable y¡, posee una raíz unitaria son LL_2, LL_3, Hadri(a), Hadri(b), HT_1, IPS_95(b), IPS_97(b) y Ztbar y Z'tbar, para estas dos últimas pruebas, sólo en el caso de los efectos fijos.
No obstante la ambigüedad de estos resultados, se procede a averiguar si los ingresos por habitante de los países de América Latina están cointegrados con el ingreso por habitante de estados Unidos, para lo cual aplicamos diversas pruebas de cointegración en panel. Los resultados se presentan en el cuadro 4.
Todas las pruebas de Pedroni (1995) rechazan la hipótesis nula de no cointegración entre los ingresos por habitante de las economías latinoamericanas y el de Estados Unidos, mientras que 2 de las 5 pruebas de cointegración de Kao (1999), específicamente las pruebas DFt, y DF*t, al igual que la de Larsson et al. (2001), no permiten rechazar la hipótesis nula de no cointegración entre estas variables; sin embargo, en este caso, la mayoría de las pruebas de cointegración sugieren que las variables en cuestión están cointegradas.
En virtud del resultado anterior se procede a estimar el parámetro β de la ecuación (7) por los métodos propuestos por Kao y Chiang (2000) para estimar variables cointegradas en panel, los cuales son: 0 Mínimos Cuadrados Ordinarios (OLS, por sus siglas en inglés); ii) Mínimos Cuadrados Ordinarios Totalmente Modificados (FMOLS); y iii) Mínimos Cuadrados Ordinarios Dinámicos (PDOLS), los cuales se presentaron en el conjunto de ecuaciones dado en (37). Los resultados de las estimaciones de β de acuerdo con estos métodos se presentan el cuadro 5.
Como se puede apreciar en el cuadro 5, a pesar de que resultaron significativas las estimaciones de la pendiente β, de acuerdo con los tres métodos, se encuentran por debajo de la unidad. En la medida en que las estimaciones de β se alejan de la unidad, estos resultados tienden a invalidar la hipótesis de la convergencia absoluta para la muestra de países de América Latina con respecto a la economía líder, la de Estados Unidos. Adicionalmente, el cuadro 6 presenta los resultados de las estimaciones de βi, tanto de manera individual como para el panel en conjunto, empleando el estimador de Mark y Sul (2003).
Las estimaciones de βi, de manera tanto individual como para el panel, resultaron estadísticamente significativas cuando la especificación del modelo incorpora una constante, con uno y dos rezagos. Mientras que cuando se incorpora una constante y una tendencia en el modelo ninguno de los parámetros estimados resultó estadísticamente significativo, como se puede ver en el cuadro 6. Con base en el cuadro 6, los países para los cuales resultaron estadísticamente significativos dichos parámetros son Brasil, Chile, Colombia, Costa Rica, República Dominicana, Ecuador, Honduras, México, Paraguay y Uruguay, cuando el modelo se especificó con un solo rezago, mientras que cuando el modelo se especificó con dos rezagos, el parámetro estimado resultó estadísticamente significativo para los mismos países, con excepción de Paraguay. El único país que mostró un parámetro cercano a la unidad fue República Dominicana, tanto con uno y dos rezagos. Chile también mostró un parámetro mayor a la unidad, en tanto que para el resto de los países, en los que el parámetro resultó estadísticamente significativo, éste resulto ser, por mucho, menor a la unidad. De esta forma, los países que mostraron una alta velocidad de convergencia fueron únicamente Chile y República Dominicana, mientras que Brasil, Colombia, Costa Rica, Ecuador, Honduras, México, Paraguay y Uruguay mostraron una baja velocidad de convergencia. De acuerdo con estos resultados no hay suficiente evidencia que tienda a soportar la hipótesis de convergencia absoluta bajo ambas pruebas empleadas (restricta e irrestricta) para la muestra de los países de América Latina en cuestión con respecto a la economía de Estados Unidos, a pesar de que para la prueba restricta, en un principio, la evidencia de las pruebas de raíces unitarias en panel sugería resultados ambiguos para decidir si la variable del diferencial del PIB per cápita de Estados Unidos, con respecto del PIB per cápita de cada uno de los países latinoamericanos, era estacionaria o no; sin embargo, encontramos suficientes razones para descartar un conjunto de las pruebas empleadas que por su carácter restrictivo podría no ser el más apropiado para probar tal hipótesis en esta variable. De esta forma, los resultados evidencian la presencia de convergencia condicional para este conjunto de países de la región en el periodo considerado.
Conclusiones
Este trabajo ha examinado la hipótesis de la convergencia hacia la economía de Estados Unidos para una muestra de 17 países de América Latina empleando pruebas de raíces unitarias y de cointegración en panel para el periodo 1970-2010. Las pruebas más apropiadas de raíces unitarias en panel aplicadas a la versión restricta de la prueba, en su mayoría, sugieren que los países de América Latina analizados en la muestra no presentan un proceso de convergencia absoluta con respecto a la economía de Estados Unidos.
Por otro lado, la mayoría de las pruebas de cointegración en panel aplicadas, específicamente las de Pedroni (1995) y tres de las cinco pruebas propuestas por Kao (1999), sugieren que los ingresos per cápita de las distintas economías consideradas mantienen una relación de equilibrio de largo plazo estable con el ingreso per cápita de Estados Unidos.
De igual forma, las estimaciones efectuadas para variables en panel cointegradas, de acuerdo con los métodos de Kao y Chiang (2000) y de Mak y Sul (2003) de la versión irrestricta en panel, permite obtener estimaciones de b, para el panel en conjunto de acuerdo con el primer método y de manera tanto agregada como desagregada con el segundo, revelaron que el parámetro estimado se encuentra por debajo de la unidad. De acuerdo con estos últimos resultados tampoco hay evidencia que soporte la hipótesis de la convergencia absoluta para la muestra de países de América Latina. Sin embargo, la presencia de cointegración entre las variables ingreso per cápita de los países de América Latina con respecto al de Estados Unidos y la significancia del parámetro b, para el panel conjunto así como para algunos de los países considerados, evidencian la presencia de un proceso de convergencia condicional para el conjunto de países de la región. El anterior resultado, como lo sugieren Cermeño y LLamosas, implica que un país pobre sólo puede alcanzar un cierto porcentaje del nivel del país rico, lo cual opaca la bondad de predicción del modelo neoclásico y pone en evidencia la realidad de la percepción cotidiana: la enorme y creciente brecha entre el nivel de vida de los países pobres y los países ricos.
Bibliografía
Amable, B. y M. Juillard (2000). The Historical Process of Convergence. Manuscript: http://pythie.cepremap.ens.fr/~amable/convergence.pdf [ Links ]
Baltagi, B. H. (2008). Econometric Analysis of Panel Data. John Wiley & Sons, 4th edition Chichester, England. [ Links ]
Barro, R., X. y Sala-i Martin (2004). Economic Growth, second edition. The MIT Press, Cambridge, MA. [ Links ]
Bernard, A. B. y S. N. Durlauf (1994). Interpreting Test of the Convergence Hypothesis. Technical Working Paper No. 159, National Bureau of Economic Research (NBER). Junio. [ Links ]
Bernard, A. B. y S. N. Durlauf (1995). Convergence in International Output. Journal of Applied Econometrics, Vol. 10, No. 2. pp. 97-108. [ Links ]
Breitung, J. (2000). The Local Power of Some Unit Root Tests for Panel Data, in: B. Baltagi (ed.), Nonstationary Panels, Panel Cointegration, and Dynamic Panels, Advances in Econometrics, Vol. 15, JAI: Amsterdam, 161-178. [ Links ]
Camarero, M., R. Flores, y C. Tamarit (2002). Multivariate Time Series Evidence of International Output Convergence in Mercosur. Computing in Economics and Finance, No. 87. [ Links ]
Cermeño, R. e I. LLamosas (2007). Convergencia del PIB per cápita de 6 países emergentes con Estados Unidos: un análisis de cointegración. EconoQuantum, Vol. 4, No. 1, pp. 59-84. [ Links ]
Cheung, Yin-Wong y A. García-Pascual (2004). Testing for Output Convergence: a Reexamination. Oxford Economic Papers, Vol. 56, No. 1, pp. 45-63 [ Links ]
Chiang, M-H. y Kao. C. (2000). Non stationary Panel Time Series Using NPT 1.1 - A User Guide. Center for Policy Research, Syracuse University. [ Links ]
Díaz-Pedroza, J. A. Sánchez-Vargas y M. A. Mendoza-González (2009). Convergencia hacia la economía regional líder en México. Un análisis de cointegración en panel. El Trimestre Económico, Vol. 76 (2), pp. 407-431. [ Links ]
Durlauf, S. (2000). Econometric Analysis and the Study of Economic Growth: a Skeptical Perspective. In: Backhouse, R., Salanti, A. (Eds.), Macroeconomics and the Real World. Oxford University Press, Oxford. [ Links ]
Durlauf, S. y P. Johnson (1995). Multiple Regimes and Cross-Country Growth Behavior. Journal of Applied Econometrics Vol. 10, No. 4, pp. 365-384. [ Links ]
Durlauf, S. y D. Quah (1999). The New Empirics of Economic Growth. Handbook of Macroeconomics, North-Holland. [ Links ]
Durlauf, S., Kourtelos, A. y Minkin, A. (2001). The Local Solow Growth Model. European Economic Review, Vol. 45, No. 4-6, pp. 928-940. [ Links ]
Easterly, W., N. Fiess y D. Lederman (2003). NAFTA and Convergence in North America: High Expectations, Big Events, Little Time. Economía: Journal of the Latin American and Caribbean Economic Association, Vol. 4, No. 1. pp. 1-53. [ Links ]
Gregory, A. W. y B. E. Hansen (1996). Residual-Based Tests for Cointegration in Models with Regime Shifts. Journal of Econometrics, Vol. 70, No. 1, pp. 99-126 [ Links ]
Hadri, K. (2000). Testing for Stationarity in Heterogeneous Panel Data. Econometrics Journal, Vol. 3, No. 2, pp. 148-161. [ Links ]
Harris, R. D. F. y E. Tzavalis (1999). Inference for Unit Roots in Dynamic Panels where the Time Dimension is Fixed. Journal of Econometrics, Vol. 91, No. 2, pp. 201-226. [ Links ]
Harris, R. y R. Sollis (2003). Applied Time Series Modelling and Forecasting. John Wiley and Sons, England. [ Links ]
Im, K., M. H. Pesaran y Y. Shin (1995). Testing for Unit Roots in Heterogeneous Panels. Manuscript, University of Cambridge. [ Links ]
Im, K. S., M. H. Pesaranand y Y. Shin (2003). Testing for Unit Roots in Heterogeneous Panels. Journal of Econometrics, Vol. 115, No. 1, pp. 53-74. [ Links ]
Kao, C. y M. H. Chiang (2000). On the Estimation and Inference of a Cointegrated Regression in Panel Data. Advances in Econometrics. [ Links ]
Larsson, R., J. Lyhagen y M. Lothgren (2001). Likelihood Based Cointegration Tests in Heterogeneous Panels. Econometrics Journal, Vol. 4, No. 1, pp. 109-142. [ Links ]
Levin, A. y C-F. Lin (1992). Unit Root Tests in Panel Data: Asymptotic and Finite-Sample Properties. Discussion Paper 92-23, University of California, San Diego. [ Links ]
Levin, A. y C-F. Lin (1993) "Unit Root Tests in Panel Data: New Results". UC San Diego Working Paper, 93-56, Diciembre 1993. [ Links ]
Linden, M. (2000). Testing Growth Convergence with Timer Series Data -a Non-Parametric Approach. International Review of Applied Economics, Vol. 14, No. 3, pp. 361-370. [ Links ]
Maddala, G. S. y S. Wu (1999). A Comparative Study of Unit Root Tests with Panel Data and New Simple Test, Oxford Bulletin of Economics and Statistics, Vol. 61, pp. 631-652. [ Links ]
Mark, N. C. y D. Sul (2003). Cointegration Vector Estimation by Panel DOLS and Long-run Money Demand. Oxford Bulletin of Economics and Statistics, Vol. 65, No. 5, pp. 655-680. [ Links ]
Pedroni, P. (1999). Critical Values for Cointegration Tests in Heterogeneous Panels with Multiple Regressors, Oxford Bulletin of Economics and Statistics, Vol. 61, No 4, pp. 653-670. [ Links ]
Pedroni, P. (2000). Fully Modified OLS for Heterogeneous Cointegrated Panels. Department of Economics Working Papers 2000-03, Department of Economics, Williams College. [ Links ]
Pedroni, P. (2004). Panel Cointegration: Asymptotic And Finite Sample Properties Of Pooled Time Series Tests With An Application To The PPP Hypothesis, Econometric Theory. Vol. 20, No. 3, pp. 597-625. [ Links ]
Phillips, P. y R. M. Hyungsik (2000). Nonstationary panel data analysis: an overview of some recent developments. Econometric Reviews, Vol. 19, No. 3, pp. 263-286. [ Links ]
Quah, D. (1993). Galton's Fallacy and the Tests of the Convergence Hypothesis. Scandinavian, Journal of Economics, Vol. 94, No. 4, pp. 427—443. [ Links ]
Quah, D. (1996a). Convergence empirics across economies with (some) capital mobility. Journal of Economic Growth, Vol. 1, No. 1, pp. 95-124. [ Links ]
Quah, D. (1996b). Empirics for Economic Growth and Convergence. European Economic Review, Vol. 40, No. 6, pp. 1353-1375. [ Links ]
Quah, D. (1997). Empirics for growth and Distribution: Stratification, Polarization, and Convergence clubs. Journal Economic Growth, Vol. 2, No. 1, pp. 27-59. [ Links ]
Solow, R. M. (1956). A Contribution to the Theory of Economic Growth. Quarterly Journal of Economics, Vol. 70, No. 1, pp. 65-94. [ Links ]
* Los autores agradecen los comentarios y sugerencias de dos dictaminadores anónimos que se dieron el tiempo de revisar de manera profesional el trabajo sometido.














