Services on Demand
Journal
Article
Indicators
Related links
Share
Revista de la Sociedad Química de México
Print version ISSN 0583-7693
Rev. Soc. Quím. Méx vol.44 n.1 Ciudad de México Jan./Mar. 2000
Investigación
An Application of the Concept of Non-Equilibrium Chemical Potential to Describe Transport Properties of Solutions
M. Mayorga,1 B. Domínguez1,2
1 Facultad de Ciencias, UAEM, Av. Instituto Literario 100, C.P. 50000 Toluca, México.
2 Instituto Tecnológico de Toluca, Av. Tecnológico s/n, Metepec, Edo. de México, México.
Recibido el 21 de enero del 2000.
Aceptado el 22 de marzo del 2000.
Abstract
We explain how the concept of thermodynamic internal degrees of freedom (TIDF) is used to extend the concept of chemical potential when some irreversible processes are present. Particularly, we choose the velocities of Brownian interacting particles as TIDF and after using the Gibbs entropy postulate and the postulates of non-equilibrium thermodynamics, we obtain the Fokker-Planck (FP) equations for the Brownian particles under a temperature gradient, which we use to obtain the corresponding momentum and energy balance equations. We analyze the diffusion regime where we obtain a novel expression for the thermal difffusion coefficient. In addition, applying a dimensional analysis to the internal energy balance equation, we find a temperature dependence of the heat conducting time that leads to conclude that the heat conduction is faster in a solution composed of suspended particles in a solvent compared with a simple liquid.
Keywords: Nonequilibrium Thermodynamics, Thermodynamic internal degrees of freedom, Thermal diffusion.
Resumen
Explicamos la manera en como se usa el concepto de grados de libertad internos termodinámicos (GLIT), para generalizar el concepto de potencial químico para el caso en que hay procesos irreversibles. A manera de ejemplo, escogemos las velocidades de partículas Brownianas interactuantes como GLIT y, después de hacer uso del postulado de Gibbs para la entropía, así como de los postulados de la termodinámica fuera de equilibrio, obtenemos las ecuaciones de Fokker-Planck (FP) para las partículas Brownianas bajo un gradiente de temperatura, posteriormente, usamos las ecuaciones de FP para obtener las ecuaciones de balance tanto para la energía como para el ímpetu. Analizamos el régimen difusivo en el cual obtenemos una expresión novedosa para el coeficiente de difusión térmica. Adicionalmente, aplicando un análisis dimensional a la ecuación de balance de la energía interna, encontramos una dependencia del tiempo de conducción térmica respecto de la temperatura, la cual nos lleva a concluir que la conducción térmica es más rápida en una solución compuesta de partículas suspendidas en un solvente en comparación a un líquido simple.
Palabras clave: Termodinámica de procesos irreversibles, grados de libertad internos termodinámicos, difusión térmica.
Dedicated to the memory of Prof. Raúl Cetina
Introduction
When Gibbs considered an heterogeneous system composed of several homogeneous subsystems (substances), such that, each other is capable of interchange mass, then a differential change in the internal energy δU of any of the substances when matter is exchanged is given by [1],
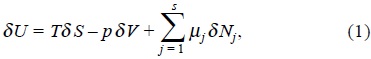
where T is the temperature of the substance δ S its change of entropy, p the pressure, δ V the change of volume during the process, δ Nj the change of mole numbers and the coefficients µj are called the chemical potentials.
The above statement even if consider the exchange of matter between different phases, it is restricted to equilibrium transformations. In order to take into account irreversible transformations, we must express the entropy change δ S as the sum of two parts [2], namely,

with δeS the change of entropy of the substance due to exchange of matter and energy with its surroundings and δiS is the entropy production inside the system by irreversible processes. In order to consider irreversible chemical reactions, we can split the change in the mole numbers δNs as a sum of two contributions,
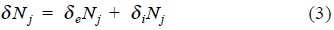
in which δeNj is the change of matter with the exterior and δiNj is the change due to irreversible chemical reactions.
Remembering that equation (1) consider reversible change of heat and matter, then we have,
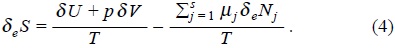
On the other hand, for a closed system where the change of mole numbers are due to irreversible chemical reactions De Donder [2] recognized the entropy production as
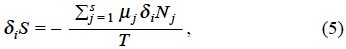
so that the second law of thermodynamics demand the next relation,

In this manner, by sum of equations (4) and (5) and using (3) and (2), we obtain the Gibbs equation (1), which shows that such statement has the necessary elements to consider the irreversibility and entropy production in chemical processes.
The extensive thermodynamic quantities are continuous functions of the space coordinates inside of the volume of the system, so writting 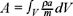 , where A represent any of the extensive quantities in the Gibbs equation and
, where A represent any of the extensive quantities in the Gibbs equation and 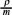 is the molar density. This permit to rewrite the eq. (2) in the form of a balance equation [2], namely,
is the molar density. This permit to rewrite the eq. (2) in the form of a balance equation [2], namely,
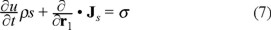
where Js is the entropy flux through the surface that envelopes the system and σ stands for the entropy production inside the volume of the system.
On the other hand, the thermodynamics of irreversible processes assume that Gibbs equation (1) is valid in a local manner, namely,
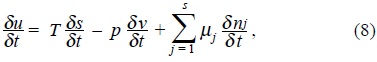
which represent a local equilibrium assumption [2]. This hypothesis is valid for small deviations δa of the thermodynamic quantity a. In order to obtain a complete description of the irreversible processes, we need the evolution equations 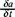 , which are the input in the eq. (8) and together with the entropy balance (7), permit us identify the entropy production and as a consequence all the irreversible processes in the system.
, which are the input in the eq. (8) and together with the entropy balance (7), permit us identify the entropy production and as a consequence all the irreversible processes in the system.
The purpose of the present article is, first of all, to attract attention in the fact that the concept of internal degrees of freedom generalizes the concept of chemical potential as was introduced by Gibbs. Secondly, as a manner of example, we choose as a system of study a chemical solution composed of Brownian particles suspended in a solvent under a temperature gradient. In this system, the internal degrees of freedom are represented by the instantaneous velocities of the tracer Brownian particles. The non-equilibrium chemical potentials that we present, permit to obtain the one and two-particle Fokker-Planck kinetic equations appropriate for the descrip tion of Brownian motion of interacting particles with an exter nal and fixed temperature gradient. Finally, we use the kinetic equations to construct the momentum and energy balance equations, which we use to obtain the collective and the ther mal diffusion coefficient of the suspended particles. The resulting collective diffusion coefficient is the usual one.
With respect to the thermal diffusion coefficient, we obtain a novel expression that takes into account the distortion of the pair correlation function of the Brownian particles due to the temperature gradient. Finally, applying a simple dimen sional analysis in the balance equation, we obtain a tempera ture dependent heat conducting time which shows that in gen eral heat conduction is faster in suspended particles compared with simple liquids.
The results presented here could serve as an alternative starting point of study of Brownian motion under a tempera ture gradient. Particularly, this study could be useful for the description of small spherical droplets immersed in a fluid subjected under a temperature gradient. This problem is of practical interest in the study of liquid alloys in materials sci ence [3, 4], and for removing unwanted gas bubbles from a liquid solution under microgravity conditions [5].
2 Gibbs entropy functional for a suspension of Brownian particles
The connection between the spontaneous thermodynamic fluctuactions and the theory of irreversible processes was set tled by Onsager and Machlup [2], nevertheless the dynamic equations for the fluctuations were not obtained from the ther modynamics of irreversible processes. Recently, the problem of fluctuations in non-equilibrium themodynamics has been revisited [6]. The scheme used admits a Gibbs entropy which depends of thermodynamic fluctuanting variables. The charac teristic time scales of such a mesoscopic variables are well separated with respect to the molecular times and are consid ered as thermodynamic internal variables. In this manner, the total system is treated as a thermodynamic system with inter nal degrees of freedom and any transformation is driven by a chemical potential which depends of such a variables. This formalism leads in a simple manner, to the behavior of fluctu ations as Markov processes described by Fokker-Planck like equations.
According to the above statements, we focus in this work in the application of the internal degrees of freedom formal ism to describe the dynamics of a system of interacting Brownian particles under a temperature gradient.
We consider a set of interacting Brownian particles of mass m suspended in a solvent which plays the role of a heat bath at rest with temperature T in a fixed volume V. We model the direct interactions between the Brownian particles as additive taken by pairs. The coordinates r1, r2 and velocities u1, u2 of any pair, correspond to the internal degrees of freedom for the system in the framework of nonequilibrium thermodynamics [6]. The Gibbs equation (1) can be extended in order to consider a reduced model of the N-particle problem into a two-particle one. In this scheme, the one and two-particle probability distribution functions are thermodynamic densities in the corresponding phase space, due to the fact that we will only include two-body interactions, namely,

and
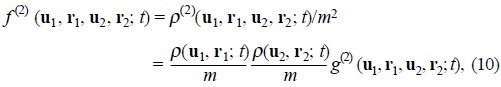
where fi(1), f(2) are the one and two-particle velocity distribution functions and g(2) is the conditional probability to find two different Brownian particles in its corresponding phase space coordinates, this function contains spatial and velocity correlations resulting from the excluded volume of solvent fluid and the soft interactions between particles.
We consider the system of Brownian particles with a mass density ρB in contact with a heat bath (solvent) of temperature T. With the previous statements, we can write the Gibbs equation for the system in a similar manner as occurs in dense gases [7],
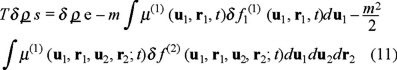
where µB = µ(1) + µ(2) represent the non-equilibrium chemical potential per unit mass for the suspended particles which is defined with the contributions of one and two-particle dynamics, explicitly,
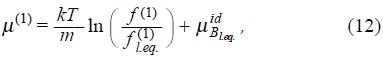
and
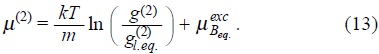
whith the equilibrium distribution functions,
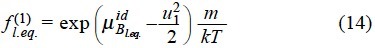
and
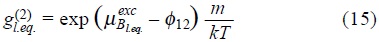
where 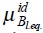 and
and 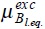 corresponds to the ideal and excess parts of the chemical potential of Brownian particles at equilibrium with the solvent, due to the interactions with the bath and between Brownian particles respectively, and φ12 is the interaction potential between particles.
corresponds to the ideal and excess parts of the chemical potential of Brownian particles at equilibrium with the solvent, due to the interactions with the bath and between Brownian particles respectively, and φ12 is the interaction potential between particles.
After the substitution of µ(1) and µ(2) in the Gibbs equation (3), and using the definition of mass density ρB = m∫ f(1)du1 for the Brownian particles, where 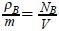 is the density number with NB the total number of Brownian particles and V the volume occupied by the solution we have,
is the density number with NB the total number of Brownian particles and V the volume occupied by the solution we have,
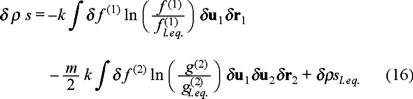
where
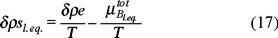
with ρ = ρs + ρB, such that ρs is the density of the solvent which is considered constant because play the role of a heat bath.
The above expression eq. (16), represents in fact the Gibbs entropy postulate where the two first terms apply for a non-equilibrium situation and the third term stands for a local equilibrium one.
3 Fokker-Planck and balance equations
In the phase space occupied by the two tracer particles, the distribution functions f (1) and f (2), obey the next continuity equations,
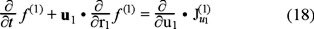
and
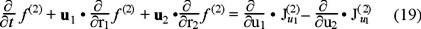
where 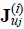 represents the currents in the velocity space resulting from the interaction with the bath (for i,j = 1) and between Brownian particles (for i = 2 and j = 1,2). On the other hand, if we apply above kinetic equations to the local equilibrium assumption for the entropy functional (16), we obtain the entropy balance equation and for the purposes of the present discussion we will center our attention in the explicit expression of the entropy production, namely,
represents the currents in the velocity space resulting from the interaction with the bath (for i,j = 1) and between Brownian particles (for i = 2 and j = 1,2). On the other hand, if we apply above kinetic equations to the local equilibrium assumption for the entropy functional (16), we obtain the entropy balance equation and for the purposes of the present discussion we will center our attention in the explicit expression of the entropy production, namely,
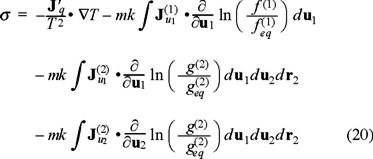
where 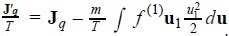 is a modified heat flux, as results from the energy conservation equation
is a modified heat flux, as results from the energy conservation equation 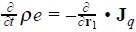 [8]. This expression has the structure of products of fluxes and forces, with the peculiarity that the last three addends are defined in the phase space.
[8]. This expression has the structure of products of fluxes and forces, with the peculiarity that the last three addends are defined in the phase space.
Based in the linear laws of thermodynamics of irreversible processes [9], we can assume linear phenomenological relations between fluxes and forces, after do this, we substitute the new expressions for the fluxes 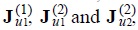 , and we obtain the one and two-particle Fokker-Planck equations,
, and we obtain the one and two-particle Fokker-Planck equations,
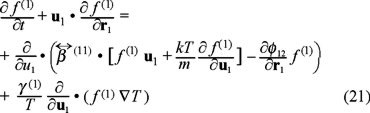
and
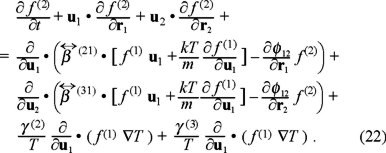
In above equations γ (i) are phenomenological coefficients which account for the coupling of the temperature gradient to the force over the Brownian particle. 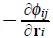 stands for the direct force from the particle j over the particle i, where φij is a pair conservative potential. On the other hand,
stands for the direct force from the particle j over the particle i, where φij is a pair conservative potential. On the other hand, 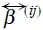 are the friction coefficients between particles and the solvent, so
are the friction coefficients between particles and the solvent, so 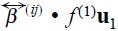 characterize the hydrodynamics interactions and
characterize the hydrodynamics interactions and 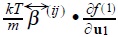 stands for the driven force that tends to homogenate the solution when both hydrodynamic and direct interactions are absent. The one-particle Fokker-Planck like kinetic equation is the same that was obtained for the case of a non-interacting suspension of Brownian particles [8], so as for N simultaneuos Brownian motion [9] [10]. It is important to emphasize that a two-particle approximation permit to us to do some estimations about transport coefficients in terms of a two-particle interaction potential. This point will be more clear in the next section.
stands for the driven force that tends to homogenate the solution when both hydrodynamic and direct interactions are absent. The one-particle Fokker-Planck like kinetic equation is the same that was obtained for the case of a non-interacting suspension of Brownian particles [8], so as for N simultaneuos Brownian motion [9] [10]. It is important to emphasize that a two-particle approximation permit to us to do some estimations about transport coefficients in terms of a two-particle interaction potential. This point will be more clear in the next section.
4 Collective and thermal diffussion
In order to illustrate how above equations works, we analyze the expression of some transport coefficients for the Brownian suspension.
Above, in fact we used the definition of the mass density ρB = m ∫ f(1)du1 on the other hand,
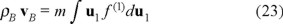
stands for the momentum mass density, so deriving respect to time with the help of the Fokker-Planck equation (21) without temperature gradient, we obtain the momentum balance, namely,
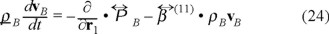
where
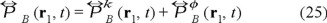
is the pressure tensor with
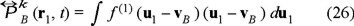
the ideal part and
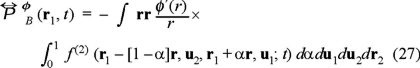
is the potential or non-ideal part, with 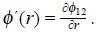
This expression obtained for the pressure tensor deserves some comments because as is well known in hydrodynamics such tensor is splitted into two terms,
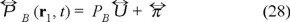
where 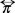 is a viscous part a quantity which is relevant when a velocity gradient is present.
is a viscous part a quantity which is relevant when a velocity gradient is present. 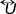 the unit tensor and PB is the hydrostatic pressure such that for an isotropic fluid corresponds to the 1/3 of the trace of the pressure tensor
the unit tensor and PB is the hydrostatic pressure such that for an isotropic fluid corresponds to the 1/3 of the trace of the pressure tensor 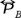 , so that, after the substitution of the velocity distribution function (14) and the pair correlation function (15) in the expressions (26) and (27), we obtain that such trace is,
, so that, after the substitution of the velocity distribution function (14) and the pair correlation function (15) in the expressions (26) and (27), we obtain that such trace is,
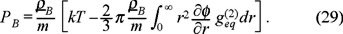
This expression is nothing else that the equation of state for a real gas or the virial equation at the second virial coefficient level in complete agreement with the statistical mechanics of dilute liquid solutions. This show that there is a one-to-one correspondence between the thermodynamics of a dilute suspension and imperfect gas theory. In this view, the Brownian interacting particles behaves as a real gas where the solvent plays the role of a heat bath. This fact was indeed recognized by van't Hoff (the first nobel prize in chemistry) in its study of osmosis, so that PB represent the osmotic pressure for the solution. After the division of the Avogadro's number of eq. (29) and keeping only the kinetic part of the pressure, we obtain

the expression for the osmotic pressure of an ideal solution, where Cm is the molar concentration of the solution and CmR = 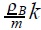 . The above equation (30) has been used to determine the number of moles of a solute in several aqueous solutions. Thus, if the mass of the solute is known, its molecular weight can be calculated. The measurement of osmotic pressure is used to determine the molecular weight of large biomolecules for which semipermeable membranes can be easily found.
. The above equation (30) has been used to determine the number of moles of a solute in several aqueous solutions. Thus, if the mass of the solute is known, its molecular weight can be calculated. The measurement of osmotic pressure is used to determine the molecular weight of large biomolecules for which semipermeable membranes can be easily found.
Analogously, the expression of osmotic pressure for non-ideal solutions (29) can be written as
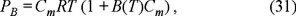
in which 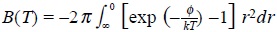 is the second virial coefficient.
is the second virial coefficient.
We move now to the transport properties. The diffusion regime is reached at time scales 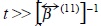 i.e., times more larger than the relaxation time
i.e., times more larger than the relaxation time 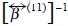 of the momentum contained in the fluid volume of size a, where a is the radius of a Brownian particle, while its mass is much larger than the mass of a molecule in the fluid.
of the momentum contained in the fluid volume of size a, where a is the radius of a Brownian particle, while its mass is much larger than the mass of a molecule in the fluid.
At this time scale the particles have slowed down by direct and hydrodynamic interactions with neighbouring Brownian particles and with the solvent respectively. Applying the above limit in the momentum balance (20), we obtain,
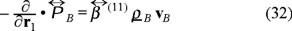
If we focus in a physical situation with no shear rate, then the viscous term 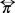 is equal to zero, in this case the pressure tensor
is equal to zero, in this case the pressure tensor 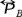 reduce to the osmotic pressure
reduce to the osmotic pressure 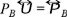 .
.
Defining the flux of particles as 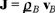 substituting the expression of the osmotic pressure (29) through the relation
substituting the expression of the osmotic pressure (29) through the relation 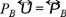 in (32), then we obtain the Fick's law,
in (32), then we obtain the Fick's law,

where we identify the collective diffusion coefficient, namely,
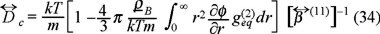
alternatively, using the equation of state (29) we obtain the usual thermodynamic relationship between the macroscopic collective diffusion coefficient and the osmotic compressibility,
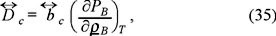
with 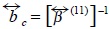 the collective mobility.
the collective mobility.
The expression (35) is in fact, a generalized Einstein rela tion, obtained in this case within the framework of Irreversible Thermodynamics. The present theory predicts the equation of state of the suspended particles as a virial one. This fact has been used as a working hypothesis to interpret some light scattering experiments in micellar emulsions [11] and lyophi lic silica particles in apolar solvents [12], and has served to test the application of liquid theories to a suspension of parti cles and its validity for all concentrations and all pair interaction potentials.
On the other hand, this relation must be complemented with the functional dependences 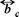 (Φ) and PB (Φ), with (Φ)
(Φ) and PB (Φ), with (Φ) 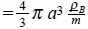 the volume fraction occupied by the Brownian particles. The expression for the mobility
the volume fraction occupied by the Brownian particles. The expression for the mobility 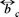 (Φ) can be obtained from a hydrodynamic theory, so for a hard sphere model with stick boundary conditions in the dilute regime, the result is
(Φ) can be obtained from a hydrodynamic theory, so for a hard sphere model with stick boundary conditions in the dilute regime, the result is 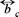 (Φ) = (6ϖηa)−1 (1-6.55Φ) [13], with η the viscosity of the supporting fluid and a the radius of the Brownian particle. A combination of stick-slip boundary conditions lead to several contributions, namely, Oseen, dipolar, short range and an extra term [14]; which helps to fit experimental [11].
(Φ) = (6ϖηa)−1 (1-6.55Φ) [13], with η the viscosity of the supporting fluid and a the radius of the Brownian particle. A combination of stick-slip boundary conditions lead to several contributions, namely, Oseen, dipolar, short range and an extra term [14]; which helps to fit experimental [11].
On the other hand, for the case where a temperature gradient is present, the momentum balance is modified as,
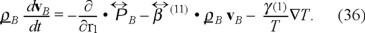
We need to obtain now the balance equation for the internal energy of the "gas" of Brownian particles ρBuB. Here we use the microscopic definition of the internal energy for the Brownian particles, namely,
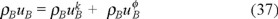
where
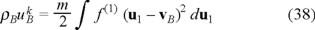
and
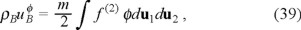
are the densities of kinetic and potential energies respectively.
Concerning the balance of internal energy, deriving respect to time above equations, after applying a Taylor's expansion around r in the distribution function f (2), we obtain,
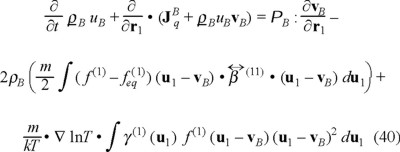
where we assumed that the friction coefficient γ (1) (u1) depends in general of the velocity of the Brownian particle, in this manner we admit a non-linear friction from the force due to the temperature gradient. On the other hand, the heat flux of the Brownian particles has three contributions, namely,
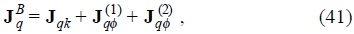
are the contributions to the heat flux from the Brownian particles, and
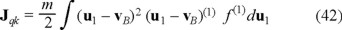
is the kinetic transport of energy referred to the mean motion vB of the Brownian particles and 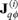 are contributions due to the interactions between particles [7].
are contributions due to the interactions between particles [7].
In this case, the momentum balance (36) and the energy balance (40) equations, according to the thermodynamics of irreversible processes [2], have the next expressions for the fluxes,
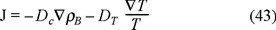
the mass flux where DT is the thermal diffusion and
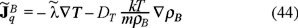
is a modified heat conduction such that,
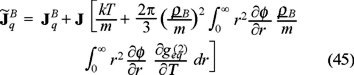
where we have used the usual Fourier's law 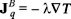 with λ the thermal conductivity of the Brownian particles.
with λ the thermal conductivity of the Brownian particles.
On the other hand, taking the diffusive regime t >> 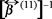 in the momentum balance (36) and comparing with (44), we obtain the expression for the thermal diffusion,
in the momentum balance (36) and comparing with (44), we obtain the expression for the thermal diffusion,
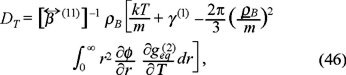
which accounts the dependence of pair correlation correlation function 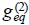 with respect to temperature, i.e. one must hope a broken of radial symmetry of this function due to the tempera ture gradient and the above result indicates the influence of such distortion in the transport of mass due to the temperature gradient.
with respect to temperature, i.e. one must hope a broken of radial symmetry of this function due to the tempera ture gradient and the above result indicates the influence of such distortion in the transport of mass due to the temperature gradient.
Now we analyze the internal energy eq. (40). Using the identity CPdT = duB, with CP the heat capacity at constant pressure, and the fact that in the diffusion regime 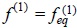 , we obtain the next evolution equation for the temperature,
, we obtain the next evolution equation for the temperature,
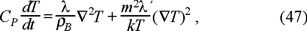
where λ´ is a modified kinetic part of the heat conductivity arises after apply the Fourier law to the expression ∫ γ(1) (u1) f(1) (u1 − vB) (u1 − vB)2 du1, namely, J′qk = − λ´ ∫ γ(1) (u1) f(1) (u1 − vB) (u1 − vB)2 du1.
Applying a dimensional analysis in the above equation (47), we obtain the next expression,

where 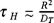 , with R a characteristic distance where there is a temperature difference,
, with R a characteristic distance where there is a temperature difference, 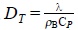 is the thermal diffusivity and
is the thermal diffusivity and 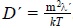 . This expression shows that in the case in which the coefficient γ(1) (u1) is velocity dependent, we should observe that the heat conducting time of the Brownian particles t is minor than the heat conducting time of a simple fluid τH, and t → τH as the temparature increases.
. This expression shows that in the case in which the coefficient γ(1) (u1) is velocity dependent, we should observe that the heat conducting time of the Brownian particles t is minor than the heat conducting time of a simple fluid τH, and t → τH as the temparature increases.
Discussion
In this paper we have explained the notion of thermodynamic internal degrees of freedom and how they lead to a definition of the corresponding non-equilibrium chemical potential. One of the important features of the internal variables is that its time scale is well separated with respect to the molecular ones. This assumption lead to a direct generalization of the local equilibrium hyphotesis from the spatio-temporal depen dence of the thermodynamic variables to an additional dependence with respect to internal variables.
Particularly, we applied the formalism to a solution com posed of a system of Brownian interacting particles dispersed in a solvent for which the corresponding Fokker-Planck equa tions were obtained. It is important to mention that even if such equations can be deduced from another non-equilibrium statistical methods, as for example the project operators [10], the approach developed here is much more simple and finally, captures the physics of the irreversible processes as was shown with the expressions of the transport coefficients.
The general form of the collective diffusion and thermal diffusion, eqs. (34) and (47), would permit to explore both, how the direct interactions and temperature influence in the mass transport of Brownian like particles.
On the other hand, we found a more rapid heat conduction in the Brownian particles in comparison with a normal simple fluid. this fact could be useful in a more general study of Brownian motion of droplets under a temperature gradient [15], a problem that has importance in the manufacturing of liquid alloys.
Acknowledgements
M. M. acknowledge partial financial support from CGIyEA of UAEM and CONACyT by the project J32094-E. B.D. acknowledge to Instituto Tecnológico de Toluca for the facilities under the program PCBITT-001.
References
1. Gibbs, J. W., The Scientific Papers of J. Willard Gibbs, Vol.1: Thermodynamics A.N. Editor (ed.). Dover, New York, 1961. [ Links ]
2. de Groot, S. R.;Mazur, P. Non-Equilibrium Thermodynamics. Dover, New York, 1984. [ Links ]
3. Ratke, L.; Ed., Immiscible Liquid Metals and Organics. Informationsgesellschaft, Oberrursel, 1993. [ Links ]
4. Ratke, L.; Diefenbach, S. Mat. Sci. Eng. 1995, R15, 263-270. [ Links ]
5. Wang, Y.; Mauri, R.; Acrivos, A. J. Fluid Mech. 1994, 261, 47-64. [ Links ]
6. Mazur, P. Physica A 1998, 261, 451-457. [ Links ] idem Physica A 1999 274, 491-504. [ Links ]
7. Romero-Salazar, L.; Mayorga, M.; Velasco, R.M. Physica A 1997, 237, 150-168. [ Links ]; Romero-Salazar, L.; Mayorga, M. Int. J. Mod. Phys. C, 1998, 9, 1293-1298. [ Links ]
8. Pérez-Madrid, A.; Rubí, J. M.; Mazur, P. Physica A 1994, 212, 231-238. [ Links ]
9. Rubí, J. M.; Mazur P., Physica A 1998, 250, 253-264. [ Links ]
10. Shea, J. M.; Oppenheim, I. J. Phys. Chem. 1996, 100, 19035-19042. [ Links ] idem, Physica A, 1997, 247, 417-443. [ Links ]
11. Agterof, W. G. M.; van Zomeren, J. A.; Vrij, A. J. Chem. Phys. Lett. 1976, 43, 363-367. [ Links ]; Cazabat, A. M.; Langevin, D. J. Chem. Phys. 1981, 74, 3148-3157. [ Links ]
12. van Helden, A. K.; Vrij, A. J. Coll. Int. Sci. 1980, 8, 312-328. [ Links ]
13. Batchelor, G. K. J. Fluid Mech. 1972, 52, 245-275. [ Links ]
14. Felderhof, B.U. J. Phys.A: Math. Gen. 1978, 11, 929-937. [ Links ]
15. Felderhof, B.U. Physica A 1997, 235, 48-55. [ Links ]














