The following is an invited keynote lecture given by Dr. Jensen at a symposium on "The History of Chemistry and Scientific Realism" held on 6-7 December 2014 in Indianapolis, IN. Since its subject matter is of great interest to chemical educators, as well as philosophers and historians of chemistry, we have chosen to reproduce it as delivered.
Those of you who read the "Call for Papers" for this symposium may recall that, among the suggestions to prospective speakers, was the injunction to focus on:
... episodes in the history of chemistry (both distant and recent) which currently have received little attention in the scientific realism debate. Especially cases where historical actors had significant explanatory and or predictive successes with a theory now rejected.
Zeroing in on both the adjective "distant" and the last sentence of this quote will immediately call to the minds of most historians of chemistry any number of historical examples that might qualify, including the phlogiston theory, the caloric theory of heat, the oxygen theory of acidity, the theory of electrochemical dualism, the reality of structural formulas etc. The only problem is that these examples can hardly be characterized as having received "little attention" - at least by historians, though perhaps the same is not equally true of philosophers of science.
Nevertheless, I have chosen instead to focus on the adjective "recent" and to relate the tale of an episode in the history of chemistry that is now just over a half century old - namely the rise and "apparent" fall of an approximate model of the chemical bond known as Linnett double-quartet theory or LDQ theory for short. I have done this in large part because it is a saga that is coextensive with my own career as both a student and teacher of chemistry, as well as one that I have followed with great interest from its very inception. There is, however, a potential problem with this choice, since 50 years may be too soon in historical terms, let alone geological terms, for such an analysis to have the proper historical and philosophical perspective that only time can provide. The dust may not yet have settled and final judgment may still be wanting.
The basic assumptions of LDQ theory
LDQ theory was the brainchild of the prominent British quantum chemist John Wilfred Linnett (Fig. 1). Trained at Oxford, he was not only a Professor of Physical Chemistry at Cambridge, but also a member of the Royal Society, President of the Faraday Society, and Vice-Chancellor of the University of Cambridge until shortly before his death from a heart attack at age 62 in 1975.
In 1961, while on sabbatical leave at the Berkeley campus of the University of California, Linnett published a paper in the Journal of the American Chemical Society entitled "A Modification of the Lewis-Langmuir Octet Rule" (Linnett, 1961) in which he suggested certain changes in G. N. Lewis’s original views on the role of the electron pair in covalent bond formation based on an explicit consideration of the effects of electron spin - a property of the electron unknown to Lewis in 1916 (Lewis, 1916).1,2 These views were further expanded upon in a short monograph (Fig. 2) published in 1964 and in about a half dozen additional articles and reviews, the last of which appeared in 1972, or about three years before Linnett’s untimely death (Linnett, 1964a, 1964b, 1964c, 1970, 1971, 1972). During this period Linnett and his students also published about a half dozen papers exploring a quantified version of the model known as nonpaired spatial orbital theory or NPSO for short (Hirst Linnett, 1961; Pauntz, 1967, Chapter 10), which showed that wave functions based on the corresponding qualitative LDQ structures uniformly gave lower energy values than did the corresponding simple valence bond (VB) and molecular orbital (MO) wave functions based on conventional Lewis structures (Brown & Linnett, 1964; Chong & Linnett, 1964; Empedocles & Linnett, 1964, Empedocles & Linnett, 1966; Gould & Linnett, 1963; Hirst & Linnett, 1962, Hirst & Linnett, 1965).
In the 1950s Linnett and his students had studied the role of electron spin in determining the distribution of the electrons in various atoms (Linnett & Poe, 1951; Mellish Linnett, 1954).3 These studies showed that electrons of like spin tended to avoid one another as much as possible whereas those of opposite spin tended to come together - an effect which Linnett referred to as "spin correlation." When one added to this the additional tendency of all electrons, whether of like or opposite spin, to avoid one another due to their identical electrical charges - an effect called "charge correlation" - one arrived at the conclusion that the cubic arrangement postulated by Lewis for the eight valence electrons of a non-bonded octet, like that around an atom of neon, was best viewed as being due to the inter-penetration of two tetrahedral spin sets, each containing four electrons of like spin (Fig. 3).
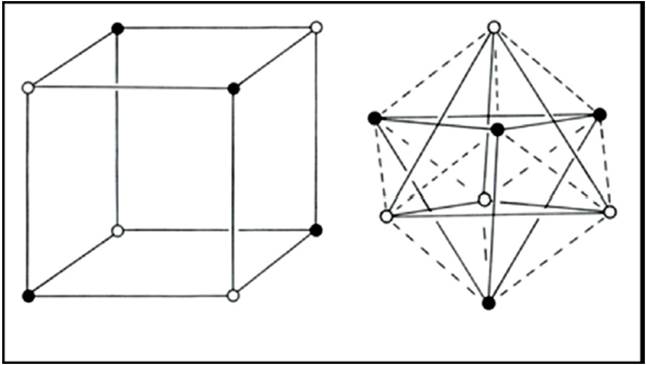
Figure 3 Left: The cubic arrangement of the two spin sets in an octet like that found in Ne(g). Black dots represent the a spin and white dots the b spin. Right: alternative view of the octet showing that it is composed of two interpenetrating fully correlated tetrahedral spin sets.
Within each spin set both spin correlation and charge correlation worked together to enforce the tetrahedral arrangement. Between the two spin sets, however, only charge correlation was operative and this could be modified during chemical bonding by the desire of the electrons to maximize their attraction to the various positive atomic cores, leading, in turn, to the formation of traditional coincident electron bonding pairs, each containing two electrons of opposite spin. As more and more of the corners of the two tetrahedral spin sets were forced into coincidence via bonding, as in the sequence HF, H2 O, NH3 and CH4 (Fig. 4), the more the remaining nonbonding corners of the spin sets were also forced into coincidence. Indeed, once two or three corners were superimposed the remaining nonbonding corners were also forced into coincidence and the result was essentially identical to Lewis’s original picture in which the bonded octet, in contrast to the non-bonded octet, always assumed the form of a single tetrahedron composed of four coincident electron pairs of opposite spin.
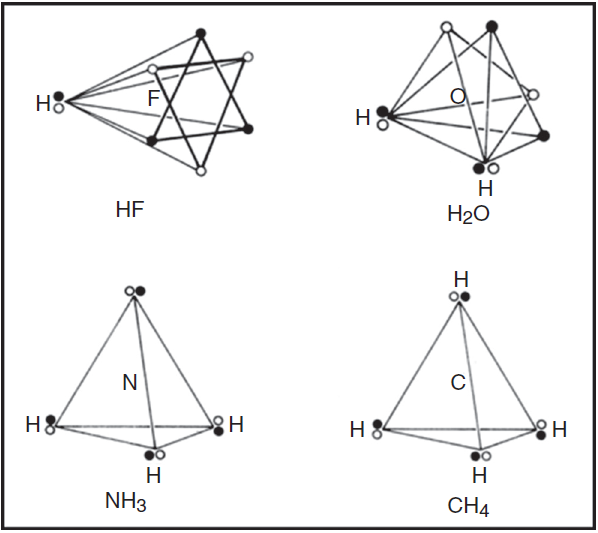
Figure 4 LDQ structures for various hydrides showing the effect of bonding on the degree of correlation between the two spin sets.
If we move on to the more complex case of the various hydrocarbons, we obtain the results in shown in Fig. 5. In the case of the alkanes, as exemplified by ethane, the tetrahedral spins sets about each carbon atom are fully coincident due to the fact that all of the electron pairs are bonding and the result is identical to that found in a conventional Lewis structure.
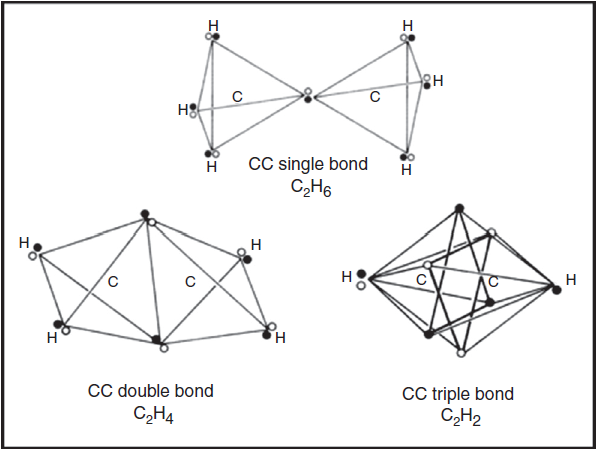
Figure 5 LDQ structures for 2c-2e CC single bonds, 2c-4e CC double bonds, and 2c-6e CC triple bonds.
Likewise, in the case of the alkenes, as exemplified by ethene, the two electron pairs in the CC double bond have been forced into coincidence by the four CH bonds, though they no longer lie on the CC axis. As a result they receive less electrostatic compensation for having been forced into coincidence than was the case for the single CC bond in ethane. Thus we would expect such bonds to be highly reactive, especially with respect to addition, which is in fact the case.
Lastly, upon examining the alkynes, as exemplified by ethyne, we encounter a surprise. Instead of the CC triple bond consisting of three fully coincident electron pairs, we find that the six bonding electrons still retain a certain degree of anticoincidence. This nicely explains why CC triple bonds are much less reactive with respect to addition than are CC double bonds, since such a reaction - leading to either a substituted alkene or a substituted alkane - would force the six electrons into coincidence and thus increase their mutual repulsions (Dale, 1969; Serartosa, 1973).
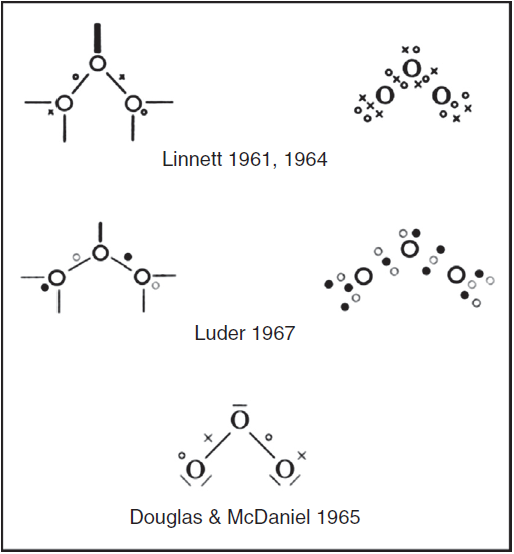
Explicitly drawing the various tetrahedral spins sets in the previous three figures, let alone showing their proper spatial orientation, is time consuming and so Linnett also developed a modification of the standard Lewis dot diagram to summarize the results of these drawings. As shown in Fig. 6 for ozone, fully coincident electron pairs were indi-cated using a thick line, anticoincident pairs using a normal line, and odd electrons using either circles or crosses in order to distinguish their spins.4 Alternatively, the lines were dispensed with and all of the electrons were shown as dots or crosses. This version greatly facilitated counting spins but failed to clearly distinguish between coincident and anticoincident electron pairs.5 Yet other authors used black and white dots to indicate the two spin sets, as we have done in the previous figures. Unfortunately Linnett’s original line symbolism made the nonbonding electron pairs look like dangling bonds, though Douglas and McDaniel had shown as early as 1965 how to make them conform more closely to the standard Lewis diagram (Douglas & McDaniel, 1965, 67-70) - a revision that Linnett would also adopt in his later publications (Linnett, 1970).
Free radicals
Free radicals are species containing one or more unpaired electrons. They have always presented a problem for conventional Lewis-VB diagrams involving debates over which atom should be assigned the unpaired electron, violations of the octet rule, and the use of multiple resonance structures. LDQ theory, on the other hand, reduces the need for resonance and reveals that the unpaired electrons often reside in the bonds and are thus equally shared. The resulting structures also reveal two classes of radicals (Fig. 7) - those like the CN or cyanogen radical that, however cleverly formulated, have too few electrons to obey the octet rule, and those like the nitrogen oxide radical which obey the octet rule. Radicals of the first class are highly reactive and experience octet completion and a net increase in the number of bonding electrons upon dimerization, whereas radicals of the second class are fairly stable since they do not experience a similar increase in the number of bonding electrons upon dimerization and often exhibit a decrease in the degree of electron anticoincidence instead.6
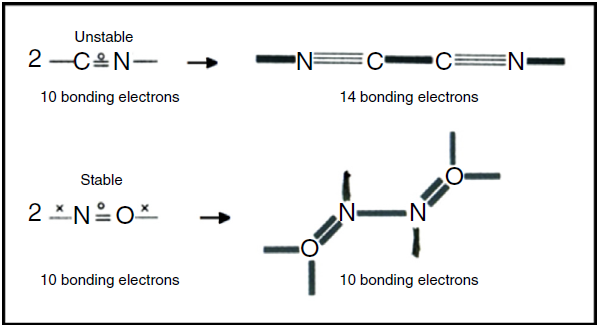
Figure 7 LDQ structures for the dimerization of the cyanogen radical versus the nitrogen oxide radical. Note the 2c-5e bonds in each radical.
A particular triumph of LDQ theory was its ability to formulate a correct structure for dioxygen gas, which is a diradical with two unpaired electrons. For electrons of one spin the tetrahedral spins sets on each of the two oxygen atoms share a common face, whereas those for the other spin share a common vertex. This leads to a double bond very different from that in ethene, containing three anti-coincident electrons of one spin and one electron of the other, or a net excess of two unpaired electrons. In contrast, neither conventional Lewis diagrams nor VB theory is able to formulate a correct structure for this common everyday substance.
Excited states
One novel application of LDQ theory was its use to represent the structures of the excited states of various molecules. This, to the best of my knowledge, has never been done using conventional Lewis structures or VB theory and, in the case of MO theory, takes the form of a single-line electron configuration rather than an actual three-dimensional structural formula. Indeed, in the case of simple diatomics, Linnett worked out in detail all of their corresponding excited-state LDQ structures and devoted an entire chapter of his 1964 monograph to this subject (Linnett, 1964a, Chapter 9). As a result of this work, he was able to develop a simple algorithm for translating the MO configurations for both excited and ground-state diatomics into their corresponding LDQ structures (Fig. 8).
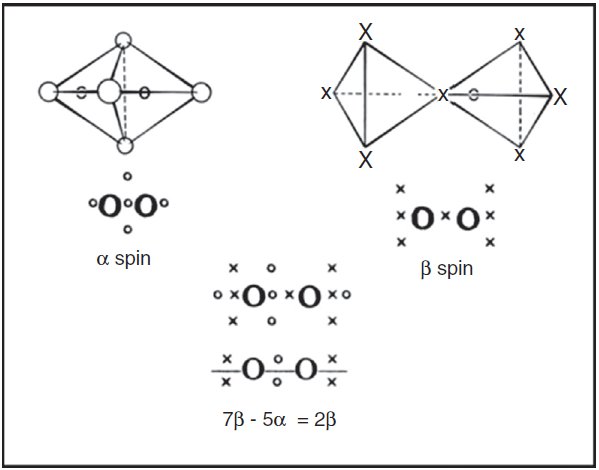
Figure 8 The LDQ structure for dioxygen gas which correctly represents it as a stable paramagnetic diradical. Note the difference between the 2c-4e bond in this species versus that found in ethene (Figure 5).
His results for the ground state and first two excited states of dioxygen gas are shown in Fig. 9. For the two excited states one of the unpaired electrons in the ground state has been flipped so that all of the electrons are now paired and their differences in energy are largely a conse-quence of differing degrees of electron coincidence. These structures also reinforce the observation that not all double bonds are created equal. That of the second excited state, for example, corresponds to the type found in ethene and is also the incorrect version assigned to ground-state dioxygen by the conventional Lewis diagram used in all undergraduate textbooks.
Hypervalence
If the octet is viewed as a tetrahedron of four coincident electron pairs and only two-electron single bonds, four-electron double bonds and six-electron triple bonds are allowed, then a given atom can be bonded at most to only four other atoms. However, many main-block compounds and ions, such as phosphorus pentachloride (PCl5), sulfur hexafluoride (SF6), and the hexafluosilicate anion (SiF6 2−) are known to contain five, six and even more covalent bonds. Such species are said to be hypervalent.
Freshman textbooks universally deal with this problem by postulating that these species can expand their octets, despite the fact that almost a half century of quantum mechanical calculations have shown that they actually obey the octet rule by using 2c-1e bonds rather than 2c-2e bonds (Jensen, 2006),7 As may be seen in Fig. 10 for phosphorus pentachloride and the polytriiodide anion, the corresponding LDQ structures for these species are fully in keeping with the results of these quantum mechanical calculations. Indeed, the LDQ structure of PCl5 may also be used to rationalize the transition state for an S N 2 displacement reaction, and the same is equally true of the hydrogen bond (Fig. 11), which may be represented using the same 2c-1e bonds rather than via two 2c-2e bonds and violation of the duplet rule.
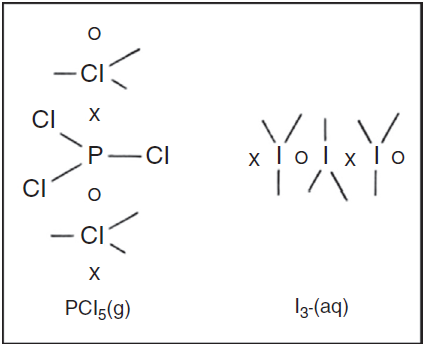
Figure 10 LDQ structure for hypervalent gaseous phosphorus pentachloride and the hypervalent aqueous polytriiodide anion. Both preserve the octet rule by invoking 2c-1e bonds.
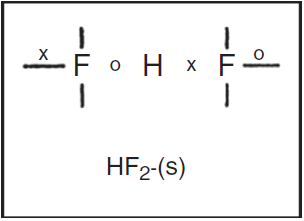
Figure 11 An LDQ structure for the symmetrical H-bond in the HF2 - anion. The duplet rule is preserved by invoking 2c-1e bonds.
These examples also call attention to a facet of LDQ theory barely touched upon in our previous examples - namely its expansion of the traditional repertoire of 2c-2e single bonds, 2c-4e double bonds, and 2c-6e triple bonds to include the 2c-1e bonds shown here, the 2c-3e bonds that appeared in the earlier LDQ structure for ozone (Fig. 6), and the 2c-5e bonds that appeared in the earlier LDQ structures for the cyanogen and nitrogen oxide radicals (Fig. 7).8
Resonance
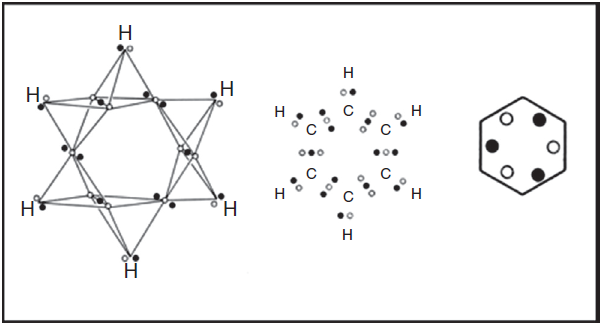
This larger bond repertoire also allowed LDQ theory to dispense with - or at least to greatly diminish - reliance on the use of resonance structures. This has been mentioned in passing with respect to the structures of free radicals and is also the case for hypervalent species, which, in the absence of octet expansion, must be represented in VB theory as examples of bond-no bond resonance (Syrkin & Dyatkina, 1950, Chapter 6). Of course the iconic example of resonance is the benzene molecule with its two contributing Kekulé structures and here LDQ theory was able to provide a single structure (Fig. 12) using 2c-3e CC bonds rather than a mixture of superimposed single and double bonds.
Summary of the achievements of LDQ theory
In concluding this all too brief survey of LDQ theory, we may summarize its more outstanding predictions and explanatory successes as follows:
It rationalizes why addition to CC triple bonds is more difficult than addition to CC double bonds.
It provides single-structure representations of many free radicals, including dixoxgen, as well as a rationale of their various stabilities.
It provides single-structure representations of excited states.
It eliminates the necessity of octet expansion for hypervalent main-block species and transition states and the necessity of duplet expansion in the case of hydrogen bonding.
It reduces and/or eliminates the use of resonance structures.
It is generally supported by quantitative quantum mechanical calculations using either the NPSO method or various modified localization techniques (Daudel, Leroy, Peeters, & Sana, 1983, pp. 258-271, 279-283; Duke, 1987).
Similar results can be obtained with VB theory and conventional Lewis diagrams only by extensive use of resonance and by MO theory only by use of a computer generated energy diagram and e/2 separate MO drawings, where e is the total number of electrons in the species.
Response of the chemical community
Given these achievements, what then was the initial response of the chemical community to LDQ theory? As is often the case with new ideas, in some circles it was simply ignored whereas in others it was enthusiastically received. Indeed, one reviewer of Linnett’s 1964 monograph characterized it as "the most important ever published in the field of chemistry" (Luder, 1966). Over the next two decades summaries of LDQ theory made their way into the mono-graph and textbook literature (Tables 1 and 2) directed at chemistry teachers and university undergraduates (Day & Selbin, 1969, pp. 201-205; Demitras, Russ, Salmon, Weber, Weiss, 1972, pp. 130-136; Douglas and McDaniel, 1965, pp. 67-70; Hildebrand & Powell, 1964, pp. 337-341, 364; Jolly, 1976, p. 29; Luder, 1967; Pickering, 1978, Chapter 7; Pimentel and Sprately, 1969, pp. 148-153) as well as into research specialty monographs (Table 3) (Rich, 1965, pp. 19-25; Lawless & Smith, 1968, pp. 221-231; Dale, 1969; Linnett, 1971; pp. 258-271, 279-283). In addition, during this same period roughly 50 papers employing and extending the model were published in the journal literature, the most important of which were by the American organic chemist, Raymond Firestone, who applied it to the study of organic reaction mechanisms (Firestone, 1968, 1969, 1970, 1971, 1972, 1973, 1976, 1980).
Table 1 Undergraduate books that included coverage of LDQ theory.
| Year | Author | Title |
| 1964 | Hildebrand & Powell | Principles of Chemistry |
| 1967 | Luder | The Electron-Repulsion Theory... |
| 1969 | Pimentel & Sprately | Chemical Bonding Clarified... |
| 1978 | Pikering | The Covalent Bond |
Table 2 Inorganic textbooks that included coverage of LDQ theory.
| Year | Author | Title |
| 1965 | Douglas & McDaniel | Concepts & Models of Inorganic Chem. |
| 1969 | Day & Selbin | Theoretical Inorganic Chemistry |
| 1972 | Demitras et al. | Inorganic Chemistry |
| 1984 | Jolly | Modern Inorganic Chemistry |
Table 3 Advanced monographs that included coverage of LDQ theory.
| Year | Author | Title |
| 1965 | Rich | Periodic Correlations |
| 1968 | Lawless & Smith | Inorganic High Energy Oxidizers |
| 1969 | Viehe | Chemistry of Acetylenes |
| 1971 | Down et al. | Essays in Structural Chemistry |
| 1983 | Daudel et al. | Quantum Chemistry |
Also of special note is the 1967 monograph (Fig. 13) by Luder listed in Table 1 which was devoted entirely to LDQ theory, though under the alternative rubric of "electron-repulsion theory" (Luder, 1967).9 Unlike Linnett, who had directed his papers and reviews at his fellow research chemists, Luder and his colleague S. Zuffanti, in a series of more than 10 papers, explicitly directed their popularization efforts at teachers of introductory chemistry at both the high school and college levels (Luder, 1967a, 1967b, 1969, 1970, 1971, 1972a, 1972b; Zuffanti, 1970; Zuffanti & Luder, 1972a, 1972b). However, not only did Luder rename the theory, he also attempted to expand it to the d- and f-block metals and advocated both abandonment of the octet rule and adoption of the controversial position that spin correlation was literally the result of magnetic attractions and repulsions between the spinning electrons (Luder, 1970, 1972b) - views which led at least one reviewer of his monograph to declare that "Luder’s book does a great disservice to Linnett and his method" (Manch, 1969).

Figure 13 Luder’s 1967 booklet on LDQ theory which he pre-ferred to call "Electron-Repulsion Theory."
The mysterious fadeout
Though this initial burst of interest appeared promising, a glance at the publication dates of the books listed in Tables 1-3 also reveals a disturbing future trend. No monographs or textbooks discussing LDQ theory have been published in the United States, Great Britain or Europe since the early 1980s, or nearly 30 years ago, with the sole exception of the 3rd edition of the 1965 inorganic text-book by Douglas and McDaniel, which appeared in 1994 (with J. Alexander as a third coauthor) (Douglas, McDaniel, & Alexander, 1994, pp. 163-166). Even then this was almost not the case. Two of the authors of this textbook were col-leagues of mine at Cincinnati and I know that they had extensive arguments over whether to continue to include the section on LDQ theory in the new edition. Those opposing its inclusion argued that it should be cut since no one taught it in the classroom, whereas those favoring its inclusion argued that this was circular since the reason no one taught it in the classroom was because it was no longer in the textbooks. On the other hand, as shown in Table 4, accounts of LDQ theory have continued to appear in textbooks published elsewhere in the world.
Table 4 Recent foreign texts that include coverage of LDQ theory.
| Year | Author | Title | Country |
| 1980 | Manchu | Theoretical Principles of Inorg. Chem. | India |
| 1987 | Cruz-Garritz et al. | Estructura Atomica | Mexico |
| 2000 | Bhagi & Raj | IAS Chemistry | India |
| 2007 | Shama | Chemistry of Chemical Bonding | India |
| 2008 | Raj | Advanced Inorganic Chemistry | India |
| 2011 | Madan & Prakash | Modern Inorganic Chemistry | India |
The same is equally true of the journal literature. Though papers mentioning the theory continue to appear - mostly by chemists interested in organic free-radical chemistry - they are few and far between and the few more general accounts that have since been published have largely appeared in obscure second-rate e-journals. Even then, it is the absence of the theory from the textbook literature for more than a generation that is the most serious problem, since, if no one is taught the theory, then it is necessarily doomed to eventually disappear from the research literature as well.
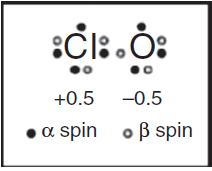
This lack of textbook coverage also eventually results in more and more examples of reinventing the wheel, as illustrated by a 2007 article that appeared in the Journal of Chemical Education proposing a "new and novel" Lewis structure for ClO and related free radicals (Fig. 14) based on computer calculations involving three different compu-tational programs (Hirsch & Kobrak, 2007). When I wrote a short "Letter to the Editor" (Jensen, 2008) pointing out that the structure in question had actually been proposed, sans a computer, 40 years earlier by Linnett using LDQ theory, the authors, while admitting that they were unaware of Linnett’s work, sidestepped the issue by suggesting that Linnett’s work might also benefit from their computational approach (Hirsch & Kobrak, 2008). These authors particularly praised the results obtained using the natural bond orbital or NBO method championed by Weinhold and Clarke which "considers electrons of opposite spin to be in separate, singly occupied orbitals," apparently equally unaware of the earlier connection between LDQ theory and the NPSO method (Weinhold & Clarke, 2012).10
Why the eclipse?
Given the list of LDQ’s predictive and explanatory successes mentioned earlier, why is it being rejected or, more accurately, neglected by the chemical community? Among the possible scientific reasons would be the charge that the theory is incompatible with quantum mechanics and there-fore fundamentally flawed, or the charge that it is not quantitative and thus incapable of being rigorously tested. But, as we have seen earlier, neither of these charges is true. The theory was initially suggested by quantum mechanical considerations and can be quantitatively tested using various versions of the NPSO method. Indeed, to the best of my knowledge, no one has ever explicitly attacked LDQ theory in the literature with a single exception. This was published in 1980 and did not question the theory’s quantum mechanical credentials,11 but rather its use of electron coincidence and anticoincidence to rationalize certain aspects of organic structure and reactivity (Langer, Trenholm, & Wasson, 1980). As things turned out, this critique was based on a flawed interpretation of LDQ theory and was easily refuted by the current author while still a lowly graduate student at the University of Wisconsin (Jensen, 1981).12
Yet another scientific objection, hinted at by several authors,13 is their assumption that the theory cannot be easily extended to large, complex molecules. Thus Pimentel in his 1969 summary of LDQ theory (Pimentel & Sprately, 1969) opined that:
... it is possible that the electron-quartet scheme was born twenty years too late to fall into everyday use. Like its electron-dot progenitor, the electron-quartet representation invokes the inert-gas magic and ignores again the energy differences between the s and p orbitals. The quartets extricate the electron-dot scheme from some of its irritating failures in simple molecules (e.g., O 2 , NO), but they are awkward to apply and sometimes require rather arbitrary choices. Meanwhile, the attention of chemists has shifted toward very complex molecules and toward much more sophisticated understanding of simpler molecules.
Likewise, Daudel et al, at the end of their 1983 summary ( Daudel et al., 1983), state that:
Linnett’s theory is very useful for understanding the existence, stability, and even the reactivity of diatomic compounds. This may be very easily extended to triatomic and tetratomic species, but not to larger systems for which its use generally becomes very intuitive and its results as ambiguous as those of resonance theory.
Possible sociological reasons for this neglect might include the charge that the theory’s originator was a unknown fringe scientist whose opinions can be safely ignored or the charge that it was published in third-rate journals or self-published books and therefore can likewise be safely ignored. But, once again, we have seen that neither of these possible charges is true. Linnett’s credentials as a first-rate quantum chemist are impeccable, the original papers all appeared in first-rate journals, and the books all had reputable publishers. Yet a third sociological rea-son might involve the charge that most textbook authors and publishers are afraid that novel departures from the standard curriculum will damage potential textbook sales and are thus leery of including new innovations. Given my earlier mention of the debates over the inclusion of LDQ theory in the 3rd edition of Douglas, McDaniel and Alexander, I think there is some truth to this charge.
This brings us finally to the question of possible philosophical reasons for this neglect - the category of most interest to the participants in this symposium. Here I am afraid I must disappoint you as I feel that the issue of scientific realism versus useful scientific "fictions" probably plays little or no role in these events, since, if one is to be perfectly honest, when it comes to quantum chemistry no one is really in a position to cast the first stone with respect to the issue of realism. Rather I would phrase the major philosophical issue to be the feeling that LDQ theory is too much of a departure from current quantitative research trends in quantum chemistry, which emphasize energy minimization and math-ematical tractability over physical coherence, pictureability and teachability. If a theory does not require that you be tethered to a computer keyboard, it cannot possibly be correct or useful. This, despite the fact that most introductory textbooks continue to use circa 1916 Lewis diagrams and most of us mentally encode our chemical intuition in the form of qualitative pictorial models rather than quantitative data. As I have often confessed to my students, when I think of molecules I do not see energy diagrams or wave functions but rather colored balls on sticks.
The relevance of LDQ theory to this issue of pictureability was well summarized by H. S. Pickering in his introductory 1978 monograph on the covalent bond, when he wrote (Pickering, 1978):
Linnett’s ideas are simple... And his ideas in no way conflict with orthodox molecular orbital theory - they are a way of presenting complex mathematical results in a clear pictorial manner... [This] may surprise some people, including some who are thoroughly familiar with a rigorous mathematical approach to bonding. But these models for molecules, such as O 2 , NO, NO 2 , N 2 O 4 , O 3 , CO 2 , CO, C 6 H 6 , arise directly from familiar molecular orbital concepts... and are not in anyway divorced from the mainstream of valency ideas.
In this regard I also feel that the classic philosophical study by Mary Hesse on the role of analogy and pictureability in the formulation of scientific models still has much to offer (Hesse, 1966).











 text new page (beta)
text new page (beta)