Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Geofísica internacional
versión On-line ISSN 2954-436Xversión impresa ISSN 0016-7169
Geofís. Intl vol.54 no.1 Ciudad de México ene./mar. 2015
Original paper
Two algorithms to compute the electric resistivity response using Green's functions for 3D structures
E. Leticia Flores-Márquez*, Andrés Tejero-Andrade**, Adrián León-Sánchez**, Claudia Arango-Galván*and René Chávez-Segura*
* Instituto de Geofísica, Universidad Nacional Autónoma de México, Circuito Exterior, Cd. Universitaria, 04510 México D.F., México. *Corresponding author: leticia@geofisica.unam.mx
** División de Ciencias de la Tierra, Facultad de Ingeniería, Universidad Nacional Autónoma de México, Circuito Interior, Cd. Universitaria, 04510 México D.F., México.
Received: June 13, 2013.
Accepted: May 05, 2014.
Published on line: December 12, 2014.
Resumen
Se introduce una solución integral para el problema directo de la respuesta geoeléctrica DC para cuerpos tri-dimensionales en un semi-espacio, mediante las funciones de Green. El primer algoritmo que se presenta se basa en el método integral de volumen (MIV); aquí, únicamente la corriente eléctrica primaria se utiliza para calcular el potencial eléctrico. El segundo caso emplea el método integral de superficie (MIS), en donde se asume que la carga inducida es debida al campo eléctrico primario. Ambos algoritmos son una combinación de integrales de volumen y de condiciones de frontera. Este artículo muestra la aplicabilidad de estos algoritmos para generar imágenes de perfiles de resistividad que reproducen algunos arreglos de electrodos para ejemplos sintéticos tradicionales, y posteriormente estas imágenes se comparan con resultados ya publicados en la literatura. Finalmente, la comparación entre estos resultados muestra que el concepto de carga inducida utilizada en MIS produce una mejor aproximación, que el esquema MIV en el cálculo del potencial eléctrico.
Palabras clave: Modelo eléctrico 3D, funciones de Green, método integral, teorema de Gauss, condiciones de frontera.
Abstract
An integral solution of the forward DC geoelectric response for three-dimensional target-bodies in a half-space, based on Green's functions, is introduced. The first algorithm presented is based on a volume integral method (VIM); here, only the primary electrical current is involved to compute the electric potential. The second one employs the surface integral method (SIM), and it is assumed the induced charge is due to the primary electrical field. Both algorithms are a combination of boundary and volume integrals. This paper shows the applicability of these algorithms to generate resistivity profile images reproducing some electrode arrays for traditional synthetic examples, and then these images were compared with already published results. Finally, the comparison between results shows the concept of induced charge used in SIM produces a better approach than VIM scheme in computing the electrical potential.
Keywords: 3D electrical model, Green's functions, integral method, Gauss theorem, Boundary conditions.
Introduction
The last three decades have been characterized by an increased use of computerized methods in the interpretation of geoelectrical data, due to the evolution of the computer systems. Most reconstructive algorithms are iterative and need a forward solution, i.e., to compute the electrical response for a given resistivity distribution and a given set array of current injection electrodes. Thus, the electrical potential needs to be calculated at a set of measured points. This forward problem consists on solving an elliptic partial differential equation (PDE): the Poisson equation, with boundary conditions. The formulation leads to solve a system with two kinds of unknown quantities: the electrical potential and a current-related quantity.
The PDE problem is usually solved with finite-difference schemes that specially has been helpful to compute the apparent electrical resistivity in a two-dimensional medium (e.g. Forsythe and Wasow, 1960; Mufti, 1976; Dey and Morrison, 1979; Marchuk, 1989; Thomée, 1989; Spitzer, 1995; Zhang et al., 1995; Loke and Barker, 1996). Another scheme extensively used in solving this PDE problem has been finite-element scheme (e.g. Coggon, 1971; Strang and Fix, 1973; Wait, 1977; Fox et al., 1980; Pridmore et al., 1980; Johnson, 1987; Ciarlet, 1991; Sasaki, 1994; Tsourlous and Ogilvy; 1999; Li and Spitzer, 2002, 2005; Marescot et al., 2008; Ren and Tang, 2010). Finite volume schemes have also produced excellent results in computing electrical resistivity (e.g. Snyder, 1976; Baliga and Patankar, 1980; Cai et al., 1991; Eskola, 1992; Perez-Flores, 1995; Perez-Flores et al., 2001; León-Sánchez, 2004; Pidlisecky et al., 2007). The methods based on a finite-element scheme have been widely studied in the past 40 years and give rise to very high-performing techniques as mixed methods (Lesur et al., 1999), or h-p methods (Babuska and Suri, 1994). Nevertheless, the already mentioned methods lead to very large systems of linear equations, which are very demanding even for the supercomputers.
One limitation in integral methods is the heterogeneity of the medium and the geometrical complexity of the bodies immersed in the modeled medium. An alternative to reduce this limitation is to propose a linearization procedure or some hypothesis about the interaction between bodies, as the weak scattering problem (Eskola, 1992; Hvozdara and Kaikkonen, 1998). Such alternatives make integral equation method a good option to solve PDE, since this method does not need linearization, even in the case of bodies with complex geometry.
The boundary-element methods (BEM) (Okabe, 1981; Nedelec, 1985, 1994; Wendland, 1987) can be thought as a particular version among the finite-element methods. An example of the application of this method to 3-D electrical modeling can be found in Poirmeur and Vasseur (1988). In this methodology, only the boundaries between media, of constant resistivity, need to be discretized and integrated. Therefore, unbounded homogeneous media are easily treated, and 3-D problems are solved using only 2-D integrals. Moreover, the boundary-element method can be coupled with standard finite element methods. The modification of the integral equations method with BEM, introduced by Hvozdara and Kaikkonen (1998), is physically more meaningful and not so much demanding on computer resources, which made the method more accessible for routine prospecting work.
This work follows the integral solution of the forward DC geoelectrical problem introduced by Hvozdara and Kaikkonen (1998; Hvozdara, 1982), which consists of interpreting the electric response of three-dimensional disturbing body of non-uniform conductivity, immersed in a planar homogeneous half-space, under the assumption of weak scattering (Figure 1). In this research two algorithms are proposed to solve this forward problem, by introducing the resistivity contrast between bodies and the homogeneous half-space and the concepts of: additive potential sources for immersed bodies and density surface charges, which result in two types of solutions: volume (VIM) and surface integral methods (SIM). SIM and BEM use the same theoretical background but the boundary surfaces in SIM are not discretized and therefore no finite element is employed. SIM and VIM are used to solve the geoelectrical problem, with mixed boundary conditions, by considering a dipole-dipole electrode array to reproduce an electric tomography profile. The results of some synthetic examples are compared with those obtained by alternative methods in solving PDE already published by other authors (e.g. Tsourlos and Ogilvy, 1999; Pridmore, 1978; Hvozdara and Kaikkonen, 1998; Perez-Flores et al., 2001).
Theoretical Setting
For a 3D heterogeneous half-space with a resistivity ρ 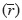 , the total electric potential for a point source at the surface z = 0, is expressed by:
, the total electric potential for a point source at the surface z = 0, is expressed by:
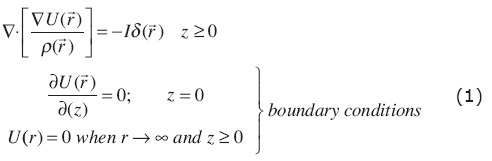
This PDE problem with boundary conditions can be rewritten as:
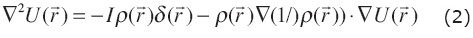
One solution for this equation can be expressed for the potential U(r) using the Green's theorems and Green's function method:
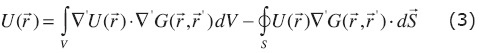
where 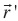 = (x', y', z') is related to local coordinates system,
= (x', y', z') is related to local coordinates system,  = (x, y, z) related to global coordinates system, and
= (x, y, z) related to global coordinates system, and 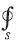 denotes the integral over the boundaries s. In particular the integral over all boundaries can be written as:
denotes the integral over the boundaries s. In particular the integral over all boundaries can be written as:
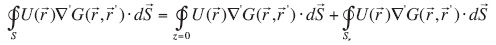
Where 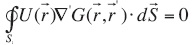 if ,
if , 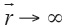 due to the boundary conditions (Hvozdara and Kaikkonen, 1998), and G is the Green's function. Green's function, G, is is defined for a half-space problem (eq. 3) for Neumann condition, where
due to the boundary conditions (Hvozdara and Kaikkonen, 1998), and G is the Green's function. Green's function, G, is is defined for a half-space problem (eq. 3) for Neumann condition, where 
 and by using
and by using 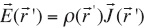 , the expression (3) can be rewritten as
, the expression (3) can be rewritten as
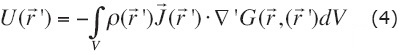
The Volume Integral Method (VIM) evaluates U(r) from equation (4), so it is necessary to know the current density function  in half-space. The computation
in half-space. The computation  of is not an easy task, since there are several types of currents involved, particularly those present in the heterogeneous half-space. The "weak scattering problem" assumes that the primary conduction current is more significant that the secondary, that is
of is not an easy task, since there are several types of currents involved, particularly those present in the heterogeneous half-space. The "weak scattering problem" assumes that the primary conduction current is more significant that the secondary, that is 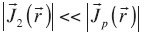 (Eskola, 1992). Due to the interaction between bodies, we can express
(Eskola, 1992). Due to the interaction between bodies, we can express 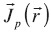 as:
as:

where sub-index s represents the location of source electrodes.
The Neumann Green function for half space can be defined, as was done by Kaufman (1992) as:
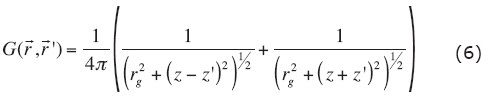
where  . Introducing this definition into eq. 4, and evaluating eq. 5 in z = 0, it becomes:
. Introducing this definition into eq. 4, and evaluating eq. 5 in z = 0, it becomes:
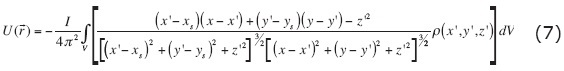
Gómez-Treviño (1987), Pérez-Flores et al. (2001) and León-Sánchez (2004) used a similar relation to estimate the apparent resistivity  in a heterogeneous half-space.
in a heterogeneous half-space.
Also 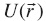 can be expressed as a surface integral, leading to the Surface Integral Method (SIM). If
can be expressed as a surface integral, leading to the Surface Integral Method (SIM). If  then eq. (4) can be rewritten as:
then eq. (4) can be rewritten as:

Here 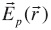 is the primary electrical field due to the point source and
is the primary electrical field due to the point source and 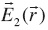 the secondary electric field due to the heterogeneities of the medium.
the secondary electric field due to the heterogeneities of the medium.
The first term of the right hand of equation (7) is equal to the primary source's potential 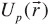 . The second term implies the whole half-space volume. This integral could be separated in volumes for each heterogeneous body, for instance if we define:
. The second term implies the whole half-space volume. This integral could be separated in volumes for each heterogeneous body, for instance if we define:
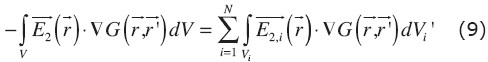
Using the next vector property for each Vi,

and assuming that the resistivity of each body within the half-space (Figure 1), is constant, then  . Thus, we can use the divergence theorem for each Vi and eq. 8 becomes:
. Thus, we can use the divergence theorem for each Vi and eq. 8 becomes:

This equation should be applied to the whole surface delimitating each immersed body; in our case, we assume the body as a regular prism. Then, the corresponding integral for the case of two contiguous prismatic bodies (b1,b2) with a common surface, is:

Where  is the unit normal vector of the surfaces (1, 2) between the two bodies.
is the unit normal vector of the surfaces (1, 2) between the two bodies.
The boundary conditions allow to define:

where  is the density surface charges and ε0 is the free-space electrical permittivity.
is the density surface charges and ε0 is the free-space electrical permittivity.
Taking into account the equations (10 to 13), the electric potential (eq. 7) is rewritten as:
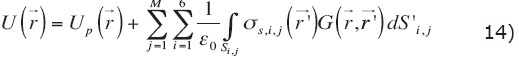
Where number 6 denotes the total number of surfaces of one prismatic body and M the number of bodies within the half-space, this eq. constitutes the SIM.
Eskola (1992) has obtained an expression similar to equation (14) using different analytical approach, under the same type of hypothesis. However, a problem to solve is to know  (the density surface charges) for each surface of the each prismatic body. Kaufman (1992) expressed
(the density surface charges) for each surface of the each prismatic body. Kaufman (1992) expressed  for two contiguous surfaces as:
for two contiguous surfaces as:

where
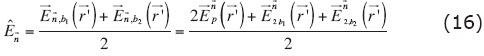
If we neglect the normal electrical secondary field in expression (16), i.e.  and,
and,  then the equation (15) becomes:
then the equation (15) becomes:

Where, R12, is the reflectivity coefficient between surfaces. This expression is the approximation of the induced surface electric charge and it is equivalent to the so-called "weak scattering problem".
Numerical Approach
Equations (6 and 14) are expressed in arbitrary coordinate systems with a fixed origin. However, to solve the corresponding integrals we redefine the origin of the coordinate system at the middle point of the prismatic body; that is the "local coordinate system". The transformation between both coordinate systems will be defined as follows: Assuming P an arbitrary point in the space, its position vector in terms of the global coordinates system is  and
and  is its position vector in terms of the local coordinate system. Consequently, the relationship between the origins for both systems is defined by
is its position vector in terms of the local coordinate system. Consequently, the relationship between the origins for both systems is defined by  (see Figure 2), that is:
(see Figure 2), that is:

Assuming isolated heterogeneous bodies immersed in a half space, let us introduce the resistivity contrast as ρ = ρc − ρm, where ρm is the resistivity of the half-space and ρc is the resistivity of the immersed body.
Then, by applying equation (6) for a quadrupole array, that is to a vertical electric sounding (VES) (where electrodes are usually named: A, B, N, M, A and B indicate current electrodes and M and N reception electrodes), the potential  associated with a point source electrode can be expressed as eq. (19). This equation also assumes the concept of additive potential sources (Orellana, 1972):
associated with a point source electrode can be expressed as eq. (19). This equation also assumes the concept of additive potential sources (Orellana, 1972):
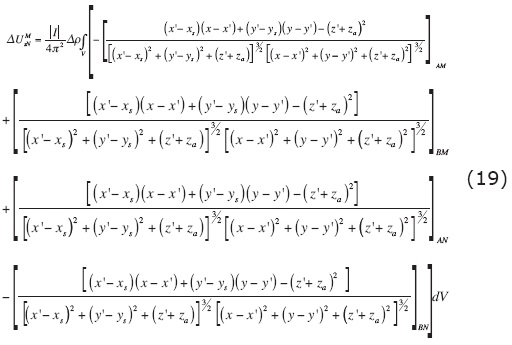
This equation allows us to compute the secondary electric potential by the volume integral method, VIM.
In the eq. 14, SIM, the density surface charges expressed in terms of the local coordinates system is:

By substituting equation (20) in equation (14), the contribution of each surface of the immersed body, to the secondary potential field for the same quadrupole array, is expressed as:

Then the apparent resistivity ρa can be expressed as:

To solve the integrals involved in equations (19 and 21) (VIM and SIM, respectively) we use the Gauss-Legendre Quadrature, by using the subroutines QGAUS and DQDAGI, that are in-cluded in the IMLS Fortran numerical libraries (Meissner, 1995; Press et al., 1992). DQDAGI subroutine makes use of Gauss-Kronrod approximation with 21 points, and by using an e-algorithm (Piessens et al., 1983), these integrals can be estimated even when the ending interval is a singularity.
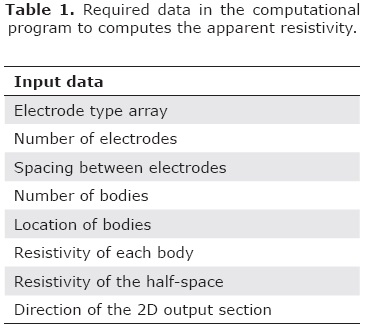
The computational program developed in this work computes the apparent resistivity profile for 3D inmersed bodies, by entering the data listed in table 1. The output data are the apparent resistivity values in an array that corresponds to a resistivity pseudo-section cutting the half-space in the input direction.
Synthetic examples
In order to illustrate the validity of the VIM and SIM developed in this work, we studied some synthetic examples and compared them to results obtained by others authors.
A stratified media, with three layers of different resistivities, constitutes the first example (Figure 3a). One case considers a middle conductor layer: 100, 10, 100 ohm-m (Figures 3b); and the other case considers a middle resistive layer: 10, 100, 10 ohm-m (Figure 3c). The results of the SIM model for a dipole-dipole array are compared (Figures 3b and 3c) to those results obtained by applying the algorithm based on the adaptative digital filtering proposed by Anderson (1979), which uses Hankel transforms. This comparison shows coincidences in the computed resistivity values at the subsurface assignation points corresponding to an electrodic separation of a = 1m, and until the level n = 14; however, after level n = 15 the results show differences between values (each level n corresponds to 0.5 m), because the computed induced charge by SIM is a poor approximation. It is important to point out that SIM is one method that needs to model closed bodies and the middle layer was considered as a body of 400 by 400 m and thickness of T = 2.5 m, the depth D = 5 m this assumption involves numerical errors that could explain the enlargement of the differences between both methods at depth (for levels n > 15 and depth > 10.5 m). But also it is important to point out the assumption of weak scattering concerns the use of Born approximation (Guozhong and Torres-Verdín, 2006) and this is also a contribution in those discrepancies, as it was signaled by Zhdanov and Fang (1996), the Born approximation produces curves of the correct shape but incorrect magnitude. In summary, we can conclude the approximation with SIM is good enough.
The second example consists of a 3D homogeneous half-space, with ρm = 100 ohm-m, and one conductor immersed prismatic body, of ρc = 20 ohm-m (Figure 4). The results of VIM method (Figure 5a) shows differences between 3 and 21 ohm-m in the lower values region compared to those computed by Pridmore (1978); while the SIM modeling of a dipoledipole array over the prism are compared (Figure 5b) to those obtained by Tsourlos and Ogilvy (1999). As it is observed, the differences between values are within 1 and 10 ohm-m. In contrast (Figure 5d), and only rise up to 14 ohm-m compared to those obtained by Tsourlos and Ogilvy (1999), Figure 5c. In spite of the differences depicted between the results of SIM and VIM, the results are good enough since the computed resistivity values do not exceed 15 ohm-m (Figures 5a and 5b). That is about 18 % of the resistivity contrast between body and half-space.
The third example showed in Figure. 6a, is constituted by the synthetic example published by Perez-Flores et al. (2001) with 4 immersed bodies of constant resistivity, ρc = 20 ohm-m. This model is based on a volume integral scheme (Perez-Flores et al., 2001) and it is similar to the hypothesis of the VIM proposed here. The comparison between SIM and model shows similar results (Figure 6b). Also, the VIM shows quite the same data for this particular case (not showed in figure); however, for general cases, we would expect bigger differences from VIM results. A possible explanation is that the electrode separation is smaller than the dimensions of the bodies.
The fourth example presented consists of two conductive bodies (Figure 7) of ρc = 20 ohm-m, immersed in a homogeneous half-space of ρm = 100 ohm-m. The bodies have the same dimensions, 10 m thick (T, in the z direction), 10 m long (L, in the x direction) and 10 m width (W, in the y direction) and both are located at 2.5 m depth (D). This example is proposed just to show the interaction between bodies by changing the separation between them, with two possibilities: closer and distant (far) bodies, with S equal to 6 m and 40 m respectively. We assume a dipole-dipole array consisting of 31 electrodes, with a 5 m distance between them. Figure 8 shows the results obtained with SIM and VIM for the case with S = 6 m. The apparent resistivity values with SIM are those expected for the bodies. In contrast, VIM's resistivity values are bigger than those expected. It is important to point out that we obtain two minimum resistivities in the location corresponding to the bodies, as we expect, those anomalies in resistivities correspond to the bodies. However, it is also observed a third anomaly at the center of the resistivity image that corresponds to a numerical feature, of a lower resistivity value. Figure 9 shows results for the case S =40 m, they are similar to those obtained for isolate bodies (Figure 6). As well as previous case, it is also observed a third anomaly at the center of the resistivity image that corresponds to a numerical feature.
In all the studies cases, we can observe, SIM produces better approach than VIM in computing the electrical potential.
Conclusions
This paper introduces two algorithms for the integral solution of the forward DC geoelectrical problem introduced by Hvozdara and Kaikkonen (1998) with mixed boundary conditions using Green's function. The two types of solutions: volume (VIM) and surface integral methods (SIM) make use of the resistivity contrast between immersed bodies and the homogeneous half-space. These methods also use the concepts of: additive potential sources for immersed bodies, and density surface charges. Both algorithms are not so much demanding on computer time and memory because they do not produce to very large systems of linear equations. This made the methods more accessible for personal computers, quotidian prospecting work and also makes it attractive for educational purposes. In particular could be useful to easily validate the field measurements interpretation.
The algorithms developed here can help in the interpretation of the field data obtained from resistivity profile methods, in two and three dimensions. The advantage of using the integral equation technique is that it is performed for each immersed body in the half space, in contrast to the usual procedure in finite-element and finite-difference methods. In order to find the induced charge, we do not need to define a grid on the surface of the body, due to the fact that we use the density surface charges on each surface.
The conducted tests with synthetic data indicated that both algorithms (SIM and VIM) produced reasonably good results compared to already published results for similar problems, obtained by other algorithms. The synthetic examples allow us to conclude that SIM produces a better approximation of the apparent resistivity values than those based on the volume integral (VIM).
These results are particularly attractive for computation in parallel, because they provide the mode to obtain the forward response for each body in simultaneous way.
Acknowledgements
This study was financed by the PAPIIT-DGAPA-UNAM research projects IN112906 and IN104006.
References
Anderson W.L., 1979, Numerical integration of related Hankel transforms of orders 0 and 1 by adaptive digital filtering, Geophysics, 44, 1287–1305. [ Links ]
Arfken G.B., Mathematical methods for physicists (Academic Press, New York 1970). [ Links ]
Babuska I., Suri M., 1994, The p and h-p versions of the finite element method, basic principle and properties, SIAM Rev. 36, 578–632. [ Links ]
Baliga B.R., Patankar S.V., 1980, A new finite-element formulation for convection-diffusion problems, Numer. Heat Transfer 3, 393–409. [ Links ]
Cai Z., Mandel J., McCormick S., 1991, The finite volume element method for diffusion equations on general triangulations, SIAM J. Numer. Anal. 28, 392–402. [ Links ]
Ciarlet P.G., The finite element method for elliptic problems, In Handbook of numerical analysis (ed. Ciarlet, P.G., and Lions, J.L.) (North-Holland Publishing Co., Amsterdam 1991) pp. 17–351. [ Links ]
Coggon J.H., 1971, Electromagnetic and electrical modelling by the finite element method, Geophysics 36, 132–155. [ Links ]
Dey A., Morrison H.F., 1979, Resistivity modeling for arbitrarily shaped three-dimensional structures, Geophysics 44, 753–780. [ Links ]
Eskola L., Geophysical interpretation using integral equations (Chapman and Hall, London 1992). [ Links ]
Forsythe G.E., Wasow R., Finite difference methods for partial differential equations (Wiley, New York 1960). [ Links ]
Fox R.C., Hohmann G.W., Killpack T.J., Rijo L., 1980, Topographic effects in resistivity and induced-polarization surveys, Geophysics 45, 75–93. [ Links ]
Gómez-Treviño E., 1987, Nonlinear integral equations for electromagnetic inverse problems, Geophysics 52, 1297–1302. [ Links ]
Ghosh D.P., 1971, The application of linear filter theory to the direct interpretation of Geoelectric Sounding Measurement, Geophys. Prosp. 19, 192–217. [ Links ]
Guozhong G., Torres-Verdín C., 2006, High-Order Generalized Extended Born Approximation for Electromagnetic Scattering. IEEE Transactions on Antennas and propagation, 54-4, 1243-1256. [ Links ]
Griffits D.H., Turburllo J., 1985, A multi-electrode array for resistivity surveying, First Break 3, 16–20. [ Links ]
Hvozdara M., 1982, Potential field of a stationary electric courrent in a stratified medium with a three-dimensional perturbing body. Stud. Geophys. Geod. 26, 161-172. [ Links ]
Hvozdara M., Kaikkonen P., 1998, An integral equation solution of the forward D.C. geoelectric problem for a 3-D body of inhomogeneous conductivity buried in a halfspace. J. of App. Geophys. 39, 95-107. [ Links ]
Johnson C., Numerical solution of partial differential equations by finite element method (Cambridge University Press, Cambridge 1987). [ Links ]
Kauffman A.A., Geophysical field theory and method: Part A - Gravitational, electric and magnetic fields (Academic Press, St. Louis 1992). [ Links ]
León-Sánchez A.M., Modelación de la respuesta eléctrica de estructuras 3D en un semiespacio conductor, BSc thesis (UNAM, México 2004). [ Links ]
Lesur V., Cuer M., Straub A., 1999, 2-D and 3-D interpretation of electrical tomography measurements - Part 1: The forward problem, Geophysics 64, 396–402. [ Links ]
Li Y., Spitzer K., 2002, 3D direct current resistivity forward modeling using finite-element in comparison with finite-difference solutions, Geophys. J. Int. 151, 924–934. [ Links ]
Li Y., Spitzer K., 2005, Finite-element resistivity modeling for 3D structures with arbitrary anisotropy, Phys. Earth Planet. Inter. 150, 15–27. [ Links ]
Loke M.H., Barker R.D., 1996, Practical techniques for 3D resistivity surveys and data inversion, Geophys. Prosp. 44, 499–523. [ Links ]
Marchuk G.I., Splitting and alternative direction techniques, In Handbook of numerical analysis (ed. Ciarlet, P.G., and Lions, J.L.) (North-Holland Publishing Co., Amsterdam 1989) pp. 197–464. [ Links ]
Marescot L., Lopes S.P., Rigobert S., Green A.G., 2008, Nonlinear inversion of geoelectric data acquired across 3-D objects using a finite-element approach, Geophysics 73, F121–F133. [ Links ]
Meissner L.P., Fortran 90 (PWS Publishing Company, Boston 1995). [ Links ]
Mufti I.R., 1976, Finite-difference resistivity modeling for arbitrarily shaped two-dimensional structures, Geophysics 41, 62–78. [ Links ]
Nedelec J.C., 1985, Equations integrales associees aux problemes aux limites eliptiques dans les domaines de R3, In Analyse mathematique et calcul numerique pour les sciences et les techniques (ed. Dautray, R., and Lions, J.L.) (Masson, Paris 1985) chap. XI, part B, pp. 645–702. [ Links ]
Nedelec J.C., 1994, New trends in the use and analysis of integral equations, Proc. Sympos. Appl. Math. 48, 151–176. [ Links ]
Okabe M., 1981, Boundary element method for the arbitrary inhomogeneities problem in electrical prospecting, Geophys. Prosp. 29, 39–59. [ Links ]
Oldenburg W.D., 1978, The interpretation of direct current resistivity measurements. Geophysics 43, 610–625. [ Links ]
Perez-Flores M.A., Méndez-Delgado S., Gomez-Treviño E., 2001, Imaging low frequency and dc electromagnetic fields using a simple linear approximation. Geophysics 66, 1067–1081. [ Links ]
Perez-Flores M.A., Inversión rápida en 2-D de datos de resistividad, magnetotelúricos y electromagnéticos de fuente controlada a bajo número de inducción, PhD thesis (Centro de Investigación Científica y de Estudios Superiores de Ensenada, Ensenada 1995). [ Links ]
Pidlisecky A., Haber E., Knight R., 2007, RESINVM3-D: A MATLAB 3-D resistivity inversion package, Geophysics 72, H1–H10. [ Links ]
Piessens R., deDoncker-Kapenga E., Uberhuber C., Kahaner C., Quadpack: a subroutine package for automatic integration (Springer-Verlag, Berlin 1983). [ Links ]
Poirmeur C., Vasseur G., 1988, Three-dimensional modeling of a hole-to-hole electrical method: Application to the interpretation of a field survey, Geophysics, 53 402–414. [ Links ]
Press W.H., Flannery B.P., Teukolsky S.A., Vetterling W.T., Numerical Recipes in Fortran (Cambridge University Press, Cambridge 1992). [ Links ]
Pridmore D., Three-dimensional modelling of electric and electromagnetic data using the finite element method, PhD thesis (University of Utah, Salt Lake City 1978). [ Links ]
Pridmore D.F., Hohmann G.W., Ward S.H., Sill W. R., 1980, An investigation of finite-element modeling for electrical and electromagnetical data in 3D, Geophysics 46, 1009–1033. [ Links ]
Ren Z., Tang J., 2010, 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method, Geophysics 75, H7–H17. [ Links ]
Roach G.F., Green's functions (Cambridge University Press, Cambridge 2004). [ Links ]
Sasaki Y., 1994, 3D resistivity inversion using the finite-element method, Geophysics 59, 1839–1848. [ Links ]
Snyder D.D., 1976, A method for modeling the resistivity and IP response of two dimensional bodies, Geophysics 41, 997–1015. [ Links ]
Spitzer K., 1995, A 3D finite-difference algorithm for DC resistivity modeling using conjugate gradient methods, Geophys. J. Inter. 123, 903–914. [ Links ]
Strang, G., and Fix, G.J., An analysis of the finite element method (Prentice-Hall, Englewood Cliffs 1973). [ Links ]
Thomée V., Finite difference methods for linear parabolic equations, In Handbook of numerical analysis (ed. Ciarlet, P.G., and Lions, J.L.) (North-Holland Publishing Co., Amsterdam 1989) pp. 5–196. [ Links ]
Tsourlos P.I., Ogilvy R.D., 1999, An algorithm for the 3-D inversion of tomographic resisitivity and induced polarisation data: preliminary results, J. Balkan Geophys. Soc. 2, 30–45. [ Links ]
Wait R., Finite element methods for elliptic problems, In The state of the art in numerical analysis (ed. Jacobs, D.) (Academic Press, St. Louis 1977) pp. 883–914. [ Links ]
Wendland W.L., Strongly elliptic boundary integral equations, In The state of the art in numerical analysis (ed. Iserles, A., and Powell, M.J.D.) (Clarendon Press, Oxford 1987) pp. 511–562. [ Links ]
Zhdanov M.S., Fang S., 1996, Quasi-linear approximation in 3-D electromagnetic modeling, Geophysics, 61-3, 646-665. [ Links ]
Zhang J., Mackie R.L., Madden T.R., 1995, 3-D resistivity forward modeling and inversion using conjugate gradients, Geophysics 60, 1313–1325. z = 0 [ Links ]














