INTRODUÇÃO
O desenvolvimento do raciocínio matemático dos alunos é uma prioridade para a aprendizagem da Matemática, claramente expressa em muitos currículos de Matemática escolar (Jeannotte e Kieran, 2017). Este valor curricular relaciona-se, em parte, com um entendimento mais amplo de raciocínio matemático do que usualmente é considerado. De facto, distinguindo-se de um significado exclusivamente centrado em aspetos lógicos, tem vindo a afirmar-se uma visão de que o raciocínio matemático integra, igualmente, a formulação e teste de novas ideias (Mata-Pereira e Ponte, 2012). A valorização do raciocínio ancora-se, igualmente, na importância que hoje se reconhece a uma formação escolar fortemente marcada pela procura de respostas para situações novas que se colocam num mundo cada vez mais complexo e que exigem raciocínio para analisar novas questões e para interpretar e justificar afirmações que permitam chegar a novas conclusões e tomar decisões. O desenvolvimento do raciocínio matemático poderá dar um contributo importante para o desenvolvimento do raciocínio em geral.
Raciocinar matematicamente é fazer inferências justificadas (Mata-Pereira e Ponte, 2018a) e envolve formulação de conjeturas, organização de testes e procura de justificações. O raciocínio matemático permite que os alunos vão além do uso de procedimentos rotineiros, dando sentido a conceitos e procedimentos matemáticos, relacionando e dando um significado coerente a diferentes aspetos da Matemática (Ball e Bass, 2003; Boaler, 2010).
Apesar da relevância de desenvolver nos alunos o seu raciocínio matemático, a investigação mostra que os professores enfrentam vários desafios quando organizam e concretizam atividades de ensino que o visam trabalhar e consolidar (Stylianides et al., 2013). De facto, os professores precisam de ter um entendimento aprofundado sobre o raciocínio matemático, quais as características dos seus principais processos, como adaptar e explorar tarefas e como conduzir discussões coletivas com os seus alunos para o promover (Ponte et al., 2013; Stein et al., 2008).
A condução das discussões coletivas é um aspeto importante da prática do professor em que se completam as ideias dos alunos, transformando-as em ideias matemáticas mais precisas e poderosas (Stein et al., 2008). A análise das discussões coletivas implica ter em atenção as ações do professor encaradas como uma intervenção ou conjunto de intervenções relacionadas entre si e realizadas com uma determinada intenção.
Este artigo visa contribuir para aprofundar o conhecimento sobre as ações do professor que incidem no desenvolvimento do raciocínio matemático dos alunos. Partimos do modelo das ações do professor na condução de discussões matemáticas proposto por Ponte, Mata-Pereira e Quaresma (2013) e Mata-Pereira e Ponte (2017; 2018a; 2018b) para caracterizar as ações de uma professora, Leonor, que ocorreram durante a discussão coletiva da tarefa “Quantas maçãs?” com uma turma de alunos de 5º ano (10-11anos). Destacamos e analisamos as características das ações da professora focando, em particular, as diretamente relacionadas com o desenvolvimento de processos de raciocínio matemático, propondo um modelo que caracteriza e integra as diferentes ações do professor sob a ótica das suas potencialidades para o desenvolvimento do raciocínio matemático e que avança características específicas destas ações. Mais especificamente, este estudo visa responder às questões: Quais as características das ações da professora que se focam no desenvolvimento do raciocínio matemático durante a condução da discussão coletiva de uma tarefa? Que relações se identificam entre as ações da professora e os processos de raciocínio matemático?
AÇÕES DO PROFESSOR NAS DISCUSSÕES COLETIVAS
A discussão coletiva na sala de aula decorrente da exploração de tarefas que visam promover o raciocínio e a resolução de problemas é fundamental para o desenvolvimento da compreensão de conceitos e para uma aprendizagem matemática com significado (NCTM, 2017). Oferece aos alunos oportunidades para partilharem ideias matemáticas e elaborarem argumentos válidos que as sustentem e clarifiquem (NCTM, 2007). À medida que os alunos tentam apresentar argumentos fundamentados para as suas ideias, esclarecem os seus próprios pensamentos e são capazes de (re)criar algumas das práticas que os matemáticos usam ao produzir argumentos e justificações (Brodie, 2010).
O reconhecimento da importância de discussões coletivas na promoção do raciocínio matemático dos alunos desencadeou, a partir dos anos 90 do Séc. XX, a realização de estudos focados na preparação e condução destes momentos de exploração das tarefas (Fraivillig et al., 1999; Lampert, 2001; Stein et al., 2008; Wood, 1999). Estes estudos realçam as ações do professor como um elemento-chave das discussões coletivas.
Fraivillig et al. (1999) organizam essas ações em três categorias: (i) Incentivar (eliciting) os alunos a apresentar os seus métodos, (ii) Apoiar (supporting) a compreensão conceptual dos alunos, (iii) Ampliar (extending) o pensamento dos alunos. Os resultados deste estudo revelam que os dois primeiros tipos de ações ocorrem, sobretudo, quando os professores pretendem ter acesso ao pensamento matemático dos alunos ou apoiar esse pensamento. Revelam, ainda, que o terceiro tipo de ações é, simultaneamente, o que contribui para um maior desenvolvimento do pensamento dos alunos e o que constitui um maior desafio para os professores.
Apoiando-se no modelo de Fraivillig et al. (1999), Cengiz et al. (2011) caracterizam de forma mais aprofundada as ações de Ampliar que ocorrem durante as discussões coletivas, analisando-as individualmente. Advertem, contudo, que as várias ações surgem muitas vezes de forma interligada e que, em alguns casos, as ações individuais a que os professores recorrem para atingir determinado fim são eficazes, mas noutros casos não o são, havendo a necessidade de desencadear uma sequência de ações. Este estudo reforça a ideia de que as ações de Ampliar, ou seja, de levar os alunos a compreender um fenómeno matemático, evoluindo para além das suas ideias iniciais, são complexas e constituem um desafio para o professor.
Ellis et al. (2013) acrescentam às três categorias de ações do professor apresentadas por Fraivillig et al. (1999), uma quarta que designam por Responder a (responding to). Esta categoria inclui ações de reação ao que os alunos dizem ou fazem, como, por exemplo, redizer uma afirmação dos alunos ou solicitar a um aluno que rediga afirmações de outros. Neste modelo de análise das ações do professor, em cada categoria são considerados dois níveis (baixo e elevado), de acordo com o potencial das ações para apoiar o raciocínio matemático dos alunos. As quatro categorias de ações são assumidamente apresentadas sequencialmente, para evitar um entendimento hierárquico quanto à sua importância no desenvolvimento do raciocínio matemático. Esta opção distancia-se da perspetiva de Fraivillig et al. (1999) ao sugerir Ampliar (extending) como o conjunto de ações que mais contribui para o desenvolvimento do pensamento dos alunos.
Também com o objetivo de estudar a condução de discussões coletivas Ponte et al. (2013) propõem o modelo de análise para as ações do professor da figura 1, que posteriormente foi também usado por Mata-Pereira e Ponte (2017; 2018a; 2018b) para analisar processos de raciocínio matemático nesta fase da exploração de tarefas.
Neste modelo, as ações do professor são organizadas em dois grupos distintos - as que se relacionam diretamente com os tópicos e processos matemáticos e as que se focam na gestão da aprendizagem (Ponte et al., 2013). É dado especial relevo às ações do primeiro grupo, que os autores designam por Convidar, Apoiar/Guiar, Desafiar e Informar/Sugerir. As ações de Convidar promovem o envolvimento inicial dos alunos na discussão ou num seu segmento (Ponte et al., 2013), incentivando os alunos a participar e a partilhar as suas resoluções (Mata-Pereira e Ponte, 2018a). As ações de Apoiar/Guiar incentivam a continuação da participação dos alunos na discussão (Ponte et al., 2013), conduzindo-os a apresentar informação (Mata-Pereira e Ponte, 2018a). Informar/Sugerir corresponde a ações em que é o próprio professor que introduz informação, sugere argumentos, ou valida respostas dos alunos (Ponte et al., 2013). Já nas ações de Desafiar, a intenção do professor é que sejam os alunos a assumir esse papel, incentivando-os a ir além do seu conhecimento prévio (Mata-Pereira e Ponte, 2018a). Este tipo de ações “coloca o aluno na situação de ser ele próprio a avançar em terreno novo, seja em termos de representações, da interpretação de enunciados, do estabelecimento de conexões, ou de raciocinar, argumentar ou avaliar” (Ponte et al., 2013, p. 59).
Com o intuito de contribuir para a construção de princípios orientadores para a promoção do raciocínio matemático dos alunos, Mata-Pereira e Ponte (2018a) recorrem a este modelo para analisar episódios de discussões coletivas e concluem que as ações do professor não surgem com uma ordem ou sequência pré-estabelecida, dependendo do que os alunos dizem ou fazem e das oportunidades que as intervenções destes geram para o desenvolvimento da aula.
RACIOCÍNIO E PROCESSOS DE RACIOCÍNIO
Sendo consensual que raciocinar é uma atividade comum a todos os seres humanos, já não é tão consensual o que se entende por raciocínio matemático. Diversos autores (Jeannotte e Kieran, 2017, Mata-Pereira e Ponte, 2018b; Oliveira, 2008) caracterizam raciocínio matemático, enfatizando alguns dos seus aspetos. Para Oliveira (2008), o raciocínio matemático refere-se a um conjunto de processos mentais complexos através dos quais se obtém conhecimento novo a partir de conhecimento prévio. Pelo seu lado, Jeannotte e Kieran (2017) associam o raciocínio matemático a um processo de comunicação que permite inferir enunciados matemáticos a partir de outros. Tendo em conta estas caracterizações de raciocínio matemático e a de Mata-Pereira e Ponte (2018b), consideramos que raciocinar matematicamente é fazer inferências justificadas.
Indo além da ideia de que raciocinar matematicamente se restringe ao raciocínio dedutivo, a investigação tem mostrado que há diferentes modos de fazer inferências justificadas, o que remete para o que Jeannotte e Kieran (2017) denominam como o “aspeto estrutural” do raciocínio. Este diz respeito ao modo como os elementos discursivos se associam num sistema ordenado que descreve os seus elementos e a relação entre eles, incluindo os diferentes tipos de raciocínio: dedutivo, indutivo e abdutivo. As autoras identificam ainda no raciocínio matemático o seu “aspeto processual”, que diz respeito a processos “meta-discursivos, isto é, que derivam narrativas sobre objetos ou relações através da exploração de relações entre objetos” (Jeannotte e Kieran, 2017, p. 9) e que estão associados a identificar padrões, procurar semelhanças e diferenças, comparar, classificar ou provar. Este aspeto processual está diretamente relacionado com o que se denomina comummente por processos de raciocínio, caracterizados por diversos autores (Lannin et al., 2011; Mata-Pereira e Ponte, 2017; Rivera e Becker, 2019). Relacionando diretamente raciocínio matemático com alguns desses processos, Lannin et al. (2011) referem que o raciocínio integra processos como conjeturar, generalizar, investigar porquê, desenvolver e avaliar argumentos.
Sendo comum a todos os autores que investigam processos de raciocínio matemático a assunção da sua complexidade, variedade e inter-relação, há diferentes caracterizações destes processos. O projeto REASON destaca os seguintes processos: generalizar, justificar, classificar, conjeturar e exemplificar. Generalizar, um processo central do raciocínio matemático, consiste em afirmar que uma ideia, propriedade ou procedimento é válido para um determinado conjunto de objetos (Carraher et al., 2008; Jeannotte e Kieran, 2017) ou afirmar que uma propriedade é comum a um grupo de objetos (Jeannotte e Kieran, 2017). Justificar, um outro processo central do raciocínio matemático, consiste em apresentar um argumento lógico baseado em ideias matemáticas para sustentar uma determinada afirmação ou refutá-la utilizando um contraexemplo (Jeannotte e Kieran, 2017). Classificar é um processo de inferência sobre classes de objetos com base nas suas propriedades e definições, que pode ser desencadeado pela procura de semelhanças ou diferenças entre objetos matemáticos (Jeannotte e Kieran, 2017) e pode corresponder, por vezes, a uma generalização. Conjeturar está associado à procura de regularidades, semelhanças ou diferenças, com o objetivo de estabelecer uma relação (Jeannotte e Kieran, 2017), envolvendo a formulação de afirmações (conjeturas) que se espera que sejam verdadeiras, mas cuja veracidade é necessário validar (Lannin et al., 2011). Finalmente, exemplificar consiste em encontrar exemplos que apoiam a procura de aspetos semelhantes e diferentes ou que apoiem a validação, sendo um processo que surge associado, e que apoia, outros processos (Jeannotte e Kieran, 2017).
A centralidade do raciocínio matemático e a importância de o desenvolver na sala de aula desde os primeiros anos é aceite por investigadores e professores, sendo essencial perceber como pode ser promovido o seu desenvolvimento. Um dos aspetos comuns às investigações sobre a temática é que o envolvimento dos alunos em discussões coletivas, em que elaboram e exprimem os seus argumentos e em que analisam a argumentação matemática de colegas e do professor, contribui para o desenvolvimento do seu raciocínio matemático (Oliveira, 2008; Stein et al., 2008). A par deste envolvimento em discussões coletivas e com elas relacionadas, identificam-se a natureza das tarefas que são propostas aos alunos (Battista, 2017; Lannin et al., 2011; Lithner, 2017) bem como ações específicas do professor durante as discussões coletivas (Ellis et al., 2018; Lannin et al., 2011; Mata-Pereira e Ponte, 2017, 2018a, 2018b) que contribuem, igualmente, para o desenvolvimento do raciocínio matemático dos alunos.
METODOLOGIA
Esta investigação segue uma metodologia interpretativa (Erickson, 1986). A recolha de dados é realizada numa turma de 5º ano de uma professora, Leonor, que participou numa oficina de formação integrada no projeto REASON. No âmbito deste projeto, que tem como objetivo geral estudar o conhecimento matemático e didático que os professores precisam para conduzir uma prática que promova o raciocínio matemático dos alunos, realizou-se esta oficina em que participaram 19 professores dos 1º e 2º ciclos do ensino básico.
A formação, orientada pelas três primeiras autoras deste artigo, incluiu seis sessões presenciais de 3 horas e dois momentos, designados por “Levar à prática”, em que cada professor explorou, na sua turma, uma tarefa por si selecionada ou adaptada e que considerava com potencialidades para desenvolver o raciocínio matemático dos seus alunos. O momento “Levar à prática I” ocorreu após a terceira sessão de formação e o “Levar à prática II” após a quinta sessão de formação. Cada um destes momentos englobou a planificação e exploração de uma tarefa na aula e a apresentação no grupo de formação que incidiu na análise dos processos de raciocínio usados pelos alunos e nas ações do professor para os desenvolver. As aulas em que foram exploradas as tarefas foram observadas e videogravadas por colegas da formação e pelas formadoras.
Leonor, com 36 anos de experiência profissional, trabalhou em grupo durante a formação com uma colega de escola, com quem partilhou as decisões sobre a escolha das tarefas e sobre a sua planificação, aspetos que o par igualmente discutiu com as formadoras. No “Levar à prática I” este par selecionou a tarefa Chupa-chupas5, analisada durante a oficina de formação, optando por substituir o contexto de distribuir chupa-chupas por distribuir maçãs (Figura 2).
Neste artigo analisamos a discussão coletiva desta tarefa ocorrida na aula de Leonor, que decorreu nos últimos 45 minutos de uma aula de 90 minutos.
A análise de dados foi realizada em três fases. Na primeira fase começou-se por garantir o rigor da transcrição, visionando a aula e introduzindo os necessários ajustamentos. Em seguida, produziu-se um relato da discussão coletiva que exclui da transcrição diálogos ou comentários não diretamente relacionados com a discussão da tarefa, como os que dizem respeito, por exemplo, a pontos de ordem relativamente a normas gerais a seguir (Professora: “Shiiiiu. Dedo no ar se quiserem contribuir ou fazer perguntas. Vá! Põem o dedo no ar. Já lá vamos”). Neste relato incluem-se notas explicativas sobre a sequência das apresentações realizadas pelos alunos e os registos realizados no quadro, de modo a traduzir o mais fielmente possível tudo o que respeita à discussão matemática da tarefa.
A segunda fase de análise incidiu sobre o relato, que foi analisado tendo como base o modelo de Ponte et al. (2013) e Mata-Pereira e Ponte (2017, 2018a, 2018b) de modo a associar as intervenções da professora a um tipo de ações consideradas por estes autores. Deste modo, as intervenções da professora que integravam o relato foram associadas à ação que ela ilustra e foi incluída uma descrição que justifica a associação realizada. Diversos exemplos são apresentados no Quadro 1.
Quadro 1 Classificação das ações da professora em três momentos da discussão coletiva e sua justificação.
| Ações | Excertos | Concretização da ação da professora |
| Convidar | Professora: Vou pedir primeiro ao vosso grupo para ir ali apresentar o que fizeram. | Convida a participar quem seguiu uma determinada estratégia. |
| (o grupo selecionado conclui que o facto de ter de dividir as maçãs por dois, sobrando uma maçã, implica que o número de maçãs é ímpar). | ||
| Desafiar | Professora: Porque é que 5 maçãs a dividir por 5 [pessoas] também não estava certo e estava também ali indicado a vermelho que não está certo. Porquê? O que é que era preciso acontecer para estar certo? | Desafia os alunos a analisar as condições do problema e perceber o que o resultado de um determinado teste implicaria para as condições iniciais do problema. |
| Guiar | Professora: Os dois amigos é que se iam dividir pelas maçãs? | Coloca uma questão para que Lourenço corrija o que está a dizer (significado dos números envolvidos). |
Na terceira fase de análise de dados, as ações da professora começaram por ser organizadas de acordo com o modelo proposto por Ponte et al. (2013) e Mata-Pereira e Ponte (2017, 2018a, 2018b) nos quatro tipos de ações centrados nos tópicos e processos matemáticos: (i) Convidar, (ii) Apoiar/Guiar, (iii) Desafiar e (iv) Informar/Sugerir. O conteúdo de cada um dos conjuntos de ações foi analisado em detalhe de modo a especificar as suas particularidades e a identificar e caracterizar as ações que diretamente se relacionam com o desenvolvimento do raciocínio matemático. Desta análise detalhada emergiu uma subdivisão de algumas das categorias inicialmente consideradas: (i) Convidar, (ii) Apoiar, (iii) Guiar, (iv) Desafiar, (v) Informar e (vi) Sugerir. As ações da professora incluídas em cada um dos tipos anteriores foram organizadas nas categorias relacionadas com processos de raciocínio (Quadro 2), que igualmente emergiram nesta fase de análise de dados.
Quadro 2 Categorias de análise de cada grupo de ações da professora.
| Ações associadas a processos de raciocínio | Processos específicos | Exemplificar | Ações que se relacionam diretamente com a explicitação de processos de exemplificar. |
| Classificar | Ações que se relacionam diretamente com a explicitação de processos de clasificar. | ||
| Conjeturar | Ações que se relacionam diretamente com a explicitação de processos de conjeturar. | ||
| Generalizar | Ações que se relacionam diretamente com a explicitação de processos de generalizar. | ||
| Justificar | Ações que se relacionam diretamente com a explicitação de processos de justificar. | ||
| Processos transversais | Meta-analisar | Ações que visam promover uma análise global dos processos usados e das conclusões a que os alunos chegam. |
Nesta fase de análise de dados foi também contabilizado o número de ações da professora incluídas em cada uma das categorias consideradas. Na secção relativa à análise de dados a ordem pela qual são apresentadas as ações da professora está associada à sua expressão nos processos de raciocínio que apoia e promove.
TIPOS DE AÇÕES DO PROFESSOR E PROCESSOS DE RACIOCÍNIO
Desafiar
No momento de discussão coletiva, embora solicitando também uma análise do que cada grupo tinha realizado ao explorar a tarefa, Leonor coloca novos desafios aos alunos que passam por justificar o que realizaram em grupo e por avançar com questões novas ou que os alunos não explicitaram na sua apresentação.
Durante a discussão coletiva, identificam-se 25 ações de desafiar (Tabela 1), organizadas em diferentes categorias, estabelecidas de acordo com as caracte-rísticas específicas de cada uma, destacando-se as que se relacionam com processos de raciocínio.
Tabela 1 Ações Desafiar com diferentes características
| Associadas a processos de raciocínio | Meta-analisar | 7 | 24 |
| Exemplificar | 4 | ||
| Justificar | 8 | ||
| Classificar | 2 | ||
| Generalizar | 3 | ||
| Não associadas a processos de raciocínio | 1 | ||
| Total | 25 | ||
Das 25 ações de desafiar identificadas apenas uma não se foca em aspetos relacionados com processos de raciocínio. Nesta ação Leonor pede aos alunos “Expliquem-se”, e ocorre depois de um conjunto de ações de guiar mais focadas e a que os alunos iam correspondendo, mas avançando com respostas pouco precisas:
| Professora: | Qual é o número maior possível, com o algarismo das unidades 7, que serve para solução do número de maçãs dentro do saco? |
| Raquel: | Tudo o que seja, tudo o que acaba em 7. |
| Professora: | Tudo. E esse tudo é o quê? |
| Raquel: | Infinitos. |
| Professora: | Não acaba, é sempre… OK. Expliquem-se. |
O desafio “expliquem-se” surge aqui como um convite para concretizar a resposta a uma questão e culmina um segmento de perguntas a que os alunos iam dando respostas imprecisas, mas que tinham como intenção compreender que não podiam indicar o maior número possível de maçãs.
De entre as 24 ações associadas a processos de raciocínio (Tabela 1), sete delas refletem desafios que Leonor explicitamente lança aos alunos para fazerem uma análise meta dos processos usados e das conclusões a que chegaram. Estas ações, que não incidem diretamente em processos de raciocínio específicos, pretendem promover uma reflexão sobre as condições expressas do problema, sobre as estratégias usadas ou sobre o que significa formular e testar uma conjetura. O Quadro 3 descreve os três tipos destas ações identificados e apresenta os excertos que ilustram as suas características.
Quadro 3 Tipos de ações Desafiar associadas a meta-analisar.
| Desafiar Meta-analisar | Descrição | Excerto |
| Os dados da tarefa | Desafia os alunos a analisar as condições do problema e perceber o que o resultado de um determinado teste implicaria para as condições iniciais do problema. | Lourenço descreve um a um os testes que realizaram, experimentando se poderiam estar no saco 3, 4 e 5 maçãs. |
| Lourenço: 3 maçãs a dividir por 5 também não dava. 5 maçãs a dividir por 5 também não dava. | ||
| Professora: Porque é que 5 maçãs a dividir por 5 também não estava certo e estava também ali indicado a vermelho que não está certo. Porquê? O que é que era preciso acontecer para estar certo? | ||
| Professora: Distribuir por 5 e? O que é que tinha de acontecer no problema? | ||
| As estratégias usadas pelos alunos. | Desafia os alunos a identificar diferenças entre resoluções da tarefa, explicando-as e/ou explicitando como poderiam modificar a sua estratégia inicial. | Depois de dois grupos terem apresentado a sua resolução da tarefa: |
| Professora: O que é que foi diferente nesses grupos? Vamos ver se vocês conseguem explicar. | ||
| Professora: Então o que é que é diferente para os grupos que, a certa altura, deixaram de estar 1 a 1 e começaram a… | ||
| Professora: Não? OK. Então reparem… então vou fazer uma pergunta diferente. O que é que vocês compreenderam de todas estas apresentações dos vossos amigos? No fundo o que é que, o que é que não conseguiram fazer enquanto estavam a trabalhar em grupo, mas que se fizessem agora fariam diferente e o que é que iam fazer? | ||
| O significado de uma conjetura. | Procura que os alunos analisem o seu modo de pensar e o associem ao processo de formular e testar conjeturas. | Professora: OK. Então o pensamento qual foi? Será que… vamos transformar o nosso pensamento numa pergunta. Qual foi essa pergunta? |
| Bia: Será que os números, que os números que têm 7, ou que acabam em 7, também dão? | ||
| Professora: Também dão? Portanto, fizemos uma pergunta e quando fazemos uma pergunta matemática ou em ciência, o que é que temos de ir fazer a seguir? Tomás. | ||
| Tomás: Testar essa coisa |
A Tabela 1 evidencia ainda que 17 das 25 ações de desafiar relacionam-se diretamente com a explicitação de processos de raciocínio matemático. Identifica ações em que Leonor desafia os alunos a (i) explicar como a procura de exemplos lhes permitiu ir encontrando soluções para a tarefa (exemplificar), (ii) refletir sobre o processo de justificar, (iii) identificar uma classificação que agrupe os valores que verificam uma determinada condição da tarefa e classificar valores e (iv) formular, criticar ou reformular generalizações. O Quadro 4 descreve estas ações e ilustra-as recorrendo a excertos ocorridos durante a discussão da tarefa.
Quadro 4 Tipos de ações Desafiar associadas a processos de raciocínio matemático.
| Descrição: | Excerto | |
| Exemplificar | Provoca uma instabilidade relativamente à justificação dos exemplos analisados ou procura que os alunos explicitem outros exemplos. | Gabriela: Nós já sabíamos que tinha de ser com número ímpar e então começamos a ver com os números ímpares que davam e quando, quando eu já estava a ter uma coisa em olho, eles iam para o 17, fizeram isso e… |
| Professora: E o 17? Enganaram-se e escreveram 17, não foi? | ||
| Bia: Depois a professora disse para nós experimentarmos com outros números, então nós fizemos com 27 e também deu. | ||
| Professora: (…) E chegaram a mais alguma conclusão? Alguém acrescentou a esta solução e àquela solução mais números? | ||
| Justificar | Procura que justifiquem porque é que um exemplo não funciona, desafia a pensar no que seria necessário para funcionar ou pergunta porque é que não testaram determinados valores. | Professora: Porque é que 5 maçãs a dividir por 5 também não estava certo e estava também ali indicado a vermelho que não está certo. Porquê? O que é que era preciso acontecer para estar certo? |
| Professora: Mas não testaram 101, 103, ... | ||
| Professora: Porque é que não podia ser 3, Lara? | ||
| Classificar | Procura que os alunos identifiquem os valores numéricos que obedecem a uma das condições do problema (números que divididos por 5 dão resto 2). | Professora: Portanto, de cinco em cinco dava que tipo de números? |
| Raquel: 7, 12, 17, o 22. | ||
| Generalizar | Desafia os alunos a reformular (é solução se tem um 7) e/ou estabelecer uma generalização. | Bia: (...) bem, então se dá o 17 ou o 27, vai dar o 7… é o número… pronto, é o número chave”. Então, experimentámos o 27. |
| Professora: Mas olhem, número chave, porque é que o 71 não dá? Também tem lá o 7. Diga, Dinis. | ||
| Professora: Qual é o número maior possível, com o algarismo das unidades 7, que serve para solução de maçãs dentro do saco? |
Guiar
Na análise das ações de Leonor durante a condução da discussão coletiva associada à tarefa “Quantas maçãs?”, foram identificadas um total de 49 ações de Guiar. A Tabela 2 apresenta a distribuição destas ações, destacando aquelas que estão associadas a processos de raciocínio dos alunos.
Tabela 2 Ações Guiar com diferentes características.
| Associadas a processos de raciocínio | Exemplificar | 2 | 14 |
| Justificar | 7 | ||
| Conjeturar | 1 | ||
| Generalizar | 4 | ||
| Não associadas a processos de raciocínio | 35 | ||
| Total | 49 |
A maior parte das ações de Guiar não estão associadas a processos de raciocínio, mas ajudam os alunos a esclarecer algo, a explicitar o que fizeram, a reformular algo ou a justificar algo, como a opção por uma estratégia de resolução, a escolha de um exemplo, ou o significado de uma expressão. Foi o que aconteceu quando uma aluna explicava como o seu grupo tinha resolvido a tarefa e é interpelada pela professora para explicitar um caminho de resolução: “Bia, o que é que fizeram a seguir?”. Por vezes, a professora pede também aos alunos que clarifiquem um passo da sua resolução. O episódio seguinte ilustra esta ação, depois de Gabriela apresentar a primeira etapa do processo de resolução do seu grupo:
| Gabriela: | Nós primeiro lemos o texto outra vez para vermos as conclusões que podíamos retirar e depois como a professora já tinha dado alguma informação eu quis dizer umas partes (impercetível) para chegarmos ao número e nós quisemos começar pelo 10 para ver quanto é que dava… e dava 0 então quer dizer que não podia ser. |
| Professora: | Dava 0 onde? Nas sobras ou… 10 a dividir por 2 amigos, era isso? |
| Ricardo: | Nas sobras. |
A questão colocada por Leonor leva Ricardo, um aluno do mesmo grupo, a clarificar a afirmação de Gabriela sobre o significado da expressão “dava 0”. A preocupação de incentivar a explicitar e, por vezes, de corrigir afirmações dos alunos, aparece, também associada à ação de Guiar:
| Lourenço: | A conta, a conta que nós fizemos foi dois, dois amigos a dividir por… e nós pu-semos um, um… sim, um pontinho… |
| Professora: | Os dois amigos é que se iam dividir pelas maçãs? |
| Lourenço: | Não, as maçãs é que iam dividir pelos amigos. |
A ação de Guiar surge também relacionada com o conduzir os alunos a justificar uma opção tomada durante o processo de resolução da tarefa. É o que acontece quando, durante a apresentação da resolução do seu grupo, Ricardo refere que experimentaram com o número 13, opção esta que Leonor pede para justificar: “Porque era ímpar, era isso?”.
A ação de Guiar aparece, ainda, relacionada com o pedido de explicitação, no momento de discussão coletiva, de um desafio colocado aos alunos durante a sua realização em grupo da tarefa, ou seja, associada à ação de desafiar (em diferido). Exemplos desta ação são ilustrados no episódio em que Leonor interpela Inês quando esta descreve o processo de resolução do seu grupo:
| Inês: | Depois ela disse que ia dar 7, nós experimentámos outra vez, fizemos os bonecos outra vez com 0, mas depois começamos a fazer a conta de dividir. |
| Professora: | Pronto, mas eu quando fui aí … (…). Eu quando fui aí vocês disseram “o 17 não dá” e eu perguntei porque é que não dá… porque a gente começou a desenhar umas bolas e depois ela disse que aquilo não dava e acabou-se e qual foi a pregunta que eu fiz? |
| Bia: | Se todos os números… |
| Professora: | Não, não. O que é que eu perguntei, Bia? |
| Bia: | Porque é que o 17 não dava. |
| Professora: | Porque é que o 17 não dava? |
| Aluno: | E depois nós fizemos uma conta de dividir e afinal dava. |
A ação evidenciada mostra que Leonor leva os alunos a concretizar, perante toda a turma, o desafio que lhes tinha colocado durante o momento de realização da tarefa em pequeno grupo e que lhes permitiu corrigir o teste relacionado com o número 17 (sobre ser ou não solução do problema) e avançar na sua resolução.
Guiar surge também em algumas ocorrências relacionada com a explicitação e concretização de processos de raciocínio. Identificam-se, assim, ações em que a professora questiona os alunos de modo a: (i) explicar o uso de exemplos que lhes permitiram encontrar, ou não, soluções da tarefa (exemplificar); (ii) concretizar a justificação de usar certos números com determinadas características (justificar); (iii) explicitar conjeturas que formularam (conjeturar); e (iv) concretizar a formulação de generalizações (generalizar). Finalmente, associada ao processo de generalizar, a ação de Guiar surge, também, sob a forma de uma questão que leva os alunos a fazer uma síntese da sua resolução, que poderá conduzir ao processo de generalizar. Este tipo de ação de Guiar destaca-se no final da discussão coletiva, quando Leonor coloca uma questão que leva os alunos a explicitar uma conclusão relacionada com a generalização das características dos números que são solução do problema.
O quadro 5 descreve estas ações relacionadas com processos de raciocínio (exemplificar, justificar, conjeturar e generalizar) e ilustra-as recorrendo a excertos ocorridos durante a discussão da tarefa
Quadro 5 Tipos de ações Guiar associadas a processos de raciocínio matemático.
| Descrição | Excerto | |
| Exemplificar | Guia os alunos a concretizar o uso de exemplos que foram testados, neste caso, 37. | Professora: Então vou fazer uma pergunta: alguém, para além deste grupo que nós vimos que chegou ao 17 e testou ali o 17, pensou que não e depois que sim? (...) Alguém passou para o 37, por exemplo? |
| Justificar | Orienta os alunos a fundamentar o uso de exemplos que lhes permitiram encontrar, ou não, soluções da tarefa. | Madalena: Primeiro começámos por explicar com o 5. Depois vimos que não dava e experimentámos com outros números |
| Neste caso é pedida a justificação de começar pelo 5. | Professora: OK. E porque é que começaram pelo 5? | |
| Conjeturar | Leva os alunos a explicitar a formulação de uma conjetura, neste caso que todos os números terminados em 7 são solução. | Ricardo: Nós chegámos ao 27. |
| Professora: Chegaram ao 27, mas quando eu passei aí, vocês já estavam a ficar com aquela ideia de quê? | ||
| Aluno: Que todos os números que acabavam em sete davam. | ||
| Generalizar | Orienta os alunos a formular uma característica comum dos números que são solução, conduzindo-os à generalização. | Pedro: E nunca dava. |
| Professora: OK, mas como chegaram ao 7? (sobre o facto de os números terem o algarismo das unidades igual a 7) | ||
| Pedro: Depois, quando chegávamos ao 7, é que dava. | ||
| No final da discussão, leva os alunos a explicitar uma conclusão sobre o que fizeram, que corresponde a generalizar (guiar síntese). | Depois de todos os grupos terem apresentado as suas resoluções, Leonor dirige-se ao último grupo e pergunta: | |
| Professora: Então eu vou perguntar a este grupo a que conclusão é que chegámos todos hoje, mesmo que não tivéssemos chegado no grupo? |
Informar
No momento de discussão coletiva, a ação de Informar descreve ou recorda o caminho seguido por um determinado grupo na resolução da tarefa, tal como ilustra o excerto seguinte:
| Professora: | Mas eles disseram, Pedro. Estiveste a ouvir, eles disseram que chegaram ao 17 e ainda chegaram ao 19, mas estavam a gastar muito tempo. (…) O que é que fal-tou? eles foram testando um a um, não é? Um a um, um a um, mas houve aqui grupos que não testaram… Quer dizer, começaram a testar 1, 2, 3, mas depois, de repente, tiveram uma ideia e foram testar essa ideia. |
Envolve, também, a correção ou inibição de caminhos de resolução que resultam de interpretações incorretas do enunciado da tarefa, tal como acontece quando Leonor chama a atenção para a impossibilidade de se considerarem cortes nas maçãs:
| Lourenço: | Depois nós concordámos que com 5 amigos… 5… nós fizemos uma maçã a dividir por 5 não dava. |
| Professora: | Eu tinha dito que não havia cá cortes das maçãs, não é? |
Salientar ou validar uma ideia a partir do que os alunos fizeram ou disseram é outra intenção subjacente à ação de Informar. No excerto seguinte, Leonor reforça uma propriedade dos “não exemplos”, ou seja, dos números que não satisfazem as condições do enunciado (o número de maçãs não pode ser divisível pelo número de pessoas).
| Lourenço: | Ah! Não sobrar nenhuma [maçã]. |
| Professora: | Pois, é que se não sobrasse nenhuma não está certo, e não sobrou nenhuma, pois não? |
| Lourenço: | Não. |
É ao salientar ou validar uma ideia a partir do que os alunos fizeram ou disseram que se evidenciam preocupações relativas a processos de raciocínio, nomeadamente à exemplificação e à generalização. A tabela 3 sintetiza o número de ações de informar observadas, destacando as que surgem associadas a processos de raciocínio.
Tabela 3 Ações Informar com diferentes características.
| Associadas a processos de raciocínio | Exemplificar | 2 | 6 |
| Generalizar | 4 | ||
| Não associadas a processos de raciocínio | 11 | ||
| Total | 17 | ||
Das 17 ações associadas a Informar, 6 relacionam-se diretamente com processos de raciocínio. As ações associadas ao processo de exemplificação evidenciam-se pela preocupação de Leonor em validar exemplos (números que satisfazem as condições do enunciado) e “não exemplos” (números que não satisfazem as condições do enunciado). Ao validar uma propriedade dos exemplos, Leonor visa uma generalização. O quadro 6 exemplifica cada uma destas situações.
Quadro 6 Ações de Informar associadas a processos de raciocínio matemático.
| Descrição | Excerto | |
| Exemplificar | Salienta/valida uma ideia a partir do que os alunos fizeram ou disseram: valida a existencia de mais exemplos (não há só um exemplo que satisfaz as condições do enunciado). | Aluno F: Mas depois chegámos ao 7 e percebemos que era um bom número e dava tudo certo, por isso, escolhemos o 7 e começámos a fazer sobre o 7. |
| Professora: Só à volta do 7? Como se houvesse só uma solução. | ||
| Salienta/valida uma ideia a partir do que os alunos fizeram ou disseram: valida “nãoexemplos” (12 e 14 não satisfazem as condições do enunciado). | Professora: Mas eles explicaram porque é que não escolheram nem o 12, nem o 14. | |
| Generalizar | Salienta/valida uma ideia a partir do que os alunos fizeram ou disseram: valida uma propriedade dos exemplos (os números ímpares que satisfazem as condições do enunciado terminam em 7). | Bia: Eu disse uma coisa “Já repararam que sempre que é ímpar e acaba em 7?”. |
| Professora: Já repararam que sempre que é ímpar, acaba em 7? |
Sugerir
No momento de discussão coletiva da aula, a ação Sugerir está associada a duas intenções. Uma tem subjacente uma possível explicação ou justificação para o que os alunos fizeram ou disseram. No excerto seguinte, Leonor sugere uma justificação (motivo) para um procedimento usado pelos alunos. Neste caso, estes repetem as condições explicitadas no enunciado e a professora avança com uma justificação para essa opção:
| Bia: | Depois nós, nós, nós vimos que com cinco amigos tinha de sobrar 2 e com 2 tinha de sobrar 1. |
| Professora: | Para se lembrarem, não é? |
A outra intenção inclui a validação ou crítica, por vezes implícita, de uma ideia ou de um caminho de resolução. No exemplo seguinte, a professora sugere que um determinado procedimento é pouco adequado, criticando-o subtilmente. Parece pretender sugerir aos alunos que o recurso a uma representação icónica no trabalho com números grandes não é uma estratégia eficaz:
| Inês: | Depois nós vimos que no 7 não dava então depois estava a experimentar o 17, mas depois a Beatriz fez o desenho no caderno dela… |
| Professora: | Muita bolinha, não era? |
| Inês: | Sim. |
| Professora: | E aqui cansaram-se… |
Em alguns casos, a ação Sugerir evidencia preocupações associadas a processos de raciocínio. Das oito ações de Sugerir identificadas no momento de discussão coletiva, quatro relacionam-se diretamente com estes processos (Tabela 4).
Tabela 4 Ações de Sugerir com diferentes características.
| Associadas a processos de raciocínio | Meta-analisar | 1 | 4 |
| Generalizar | 3 | ||
| Não associadas a processos de raciocínio | 4 | ||
| Total | 8 | ||
Tal como mostra a tabela 4, ocorre um processo Meta-analisar focado nas estratégias utilizadas pelos alunos. Mais concretamente, Leonor chama a atenção que os caminhos de resolução até ao momento apresentados pelos grupos têm implícitos processos de raciocínio que são concretizados sequencialmente: exemplificar, observar um padrão, conjeturar e testar. O quadro seguinte descreve estas ações relacionadas com processos de raciocínio (meta-analisar e generalizar) e ilustra-as recorrendo a excertos ocorridos durante a discussão da tarefa.
Quadro 7 Ações de Sugerir associadas a processos de raciocínio matemático.
| Descrição | Excerto | |
| Meta-analisar as estratégias usadas pelos alunos. | Sugere uma estratégia, validando-a: Chama a atenção dos alunos que ao observarmos uma regularidade, produzimos uma conjetura e tentamos testá-la, parando o processo de exemplificação. | Professora: Testar essa nossa ideia e houve alguém que disse experimentar, fazer as contas com esses números que estão na nossa ideia e isso poupa-nos, se tivermos uma boa ideia a certa altura porque estamos a reparar que há ali algunas coisas que são parecidas, poupa-nos trabalho. Já não gastamos tanto tempo em vez de ir de um em um podemos testar essa nossa ideia, certo? |
| Generalizar | Sugere a possibilidade de vir a analisar a generalização proposta (os números terminados em 7 experimentados satisfazem as condições do problema). | Um aluno: Todos os números que acabavam em sete davam. |
| Professora: Talvez houvesse aqui uma história, que o 7 seria uma boa referência, se bem que eu já aí vou voltar numa outra questão. |
Convidar
Foram identificadas 11 ações de Convidar. Uma parte destas ações tem subja-cente uma intenção associada à Matemática e conduz à participação de deter-minados alunos ou grupos:
| Professora: | Quem é que aqui testou com números relativamente altos? |
| (…) | |
| Professora: | Ouçam uma coisa, vocês em algum momento experimentaram números pares? A dividir pelo dois ou pelo cinco? |
O primeiro excerto ilustra um convite à participação dos alunos que testaram números com determinadas características, neste caso, números pares, enquanto o segundo exemplifica um apelo à intervenção daqueles que experimentaram números com uma certa ‘grandeza’.
Durante a discussão coletiva, identificam-se um total de quatro ações deste tipo, não se destacando alguma que explicitamente traduza preocupações associadas a processos de raciocínio dos alunos.
É de salientar que nem sempre é evidente ou explícita uma intenção da professora relacionada com a Matemática quando convida alunos a participar na discussão. Identificam-se sete deste tipo de ações cuja intenção é gerir as intervenções dos alunos na discussão, quer dando voz especificamente a alguns deles quer solicitando globalmente a participação dos alunos da turma na discussão. São exemplos destas ações as seguintes intervenções de Leonor:
| Professora: | Espera que eu quero ouvir a Gabriela, ou a Bia, ou a Inês, ou o Ricardo. |
| (…) | |
| Professora: | Alguém quer fazer alguma pergunta? |
O primeiro caso ilustra uma ação em que a professora dá voz, explicitamente aos elementos de um grupo de alunos enquanto o segundo exemplifica uma ação em que solicita a participação global dos alunos da turma na discussão. Tal como era expectável, neste caso, nenhuma destas ações surge explicitamente associada a processos de raciocínio dos alunos.
Apoiar
Foram identificadas um total de 12 ações de Apoiar por parte de Leonor. Este tipo de ação corresponde a enfatizar uma opção, um caminho, uma resposta dos alunos bem como a redizer o que os alunos disseram. No caso desta professora, muitas das suas intervenções são iniciadas com a expressão “OK”, dando um sinal inequívoco aos alunos de que apoia e está de acordo com o que estes acabaram de dizer:
| Bia: | Sim e depois, pronto, fizemos o número ímpar e a partir daí fizemos ímpar… |
| Professora: | OK. Foram experimentando. |
| Bia: | Sim. |
Neste episódio, para além de validar o que o os alunos efetuaram, Leonor enfatiza ainda o caminho de resolução que estes seguiram, dizendo “foram experimentando”. As ações observadas deste tipo não surgem associadas a processos de raciocínio dos alunos.
INTER-RELAÇÃO E SEQUENCIALIDADE DAS AÇÕES DA PROFESSORA
Nas secções anteriores analisámos as ações de Leonor durante o momento de discussão coletiva, tanto as que se ligam diretamente a processos de raciocínio matemático como as que apenas têm como intenção a orquestração das inter-venções dos alunos. Embora esta análise tenha sido realizada ação a ação tendo como objetivo a apresentação de evidências associadas a cada uma, no momento de discussão coletiva foram identificados padrões entre elas, tanto no que se refere à sua relação como à sua sequencialidade.
Duas ações que se interligam no discurso da professora, no momento de discussão coletiva, são as de Apoiar e Guiar, tal como acontece neste episódio:
| Professora: | E depois foram dividir. Ah, OK. Então, quando dividiram, o resto era…? |
| Inês: | O resto era…O do 10 era 0 e o do dois acho que era… |
| Gabriela: | 1. |
Esta interligação parece ter uma dupla intenção, por um lado, valida o que os alunos disseram (Apoiar) e, por outro, questiona-os, de modo a que estes explicitem algo na sua apresentação (Guiar), neste caso sobre o valor do resto que obtiveram quando efetuaram diversas divisões. Em todos os casos analisados desta associação de ações da professora, num total de quatro, identifica-se, também, esta sequencialidade - Leonor começa por apoiar o discurso dos alunos, colocando depois uma questão no sentido de os guiar na sua intervenção.
A ação Apoiar surge, ainda, num total de oito vezes, associada a Desafiar. Frequentemente, o apoio é verbalizado apenas pela expressão “OK” que valida o caminho seguido pelos alunos até aí, antes de lhes colocar o próximo desafio:
| Raquel: | Fizemos as contas e depois… dão os setes, então nós pensámos “então vamos fazer um número maior” pensamos em 100 e depois eu assim “então, mas se dá 7, se fizermos 107?” e fizemos 107. |
| Professora: | OK. Então o pensamento qual foi? Será que… vamos transformar o nosso pensa-mento numa pergunta. Qual foi essa pergunta? |
| Bia: | Será que os números que têm 7, ou que acabam em 7, também dão? |
Neste excerto, Apoiar é seguido de um desafio associado à formulação de uma conjetura sobre as características dos números que são solução do problema.
AÇÕES DA PROFESSORA DURANTE A DISCUSSÃO COLETIVA
A análise de todas as ações de Leonor durante a discussão coletiva permite identificar a frequência observada em cada uma das categorias identificadas, distinguindo as ações em que foi observada uma associação a processos de raciocínio das que, pelas suas características, não o podem estar (tabela 5).
Tabela 5 Frequência de cada tipo de ação por categoria analisada.
| Ações | Associadas a processos de raciocínio | Não associadas a processos de raciocínio | ||||||
| Processos | ||||||||
| Exemplificar | Classificar | Justificar | Generalizar | Conjeturar | Meta | Total | ||
| Desafiar | 4 | 2 | 8 | 3 | - | 7 | 24 | 1 |
| Guiar | 2 | - | 7 | 4 | 1 | - | 14 | 35 |
| Informar | 2 | - | - | 4 | - | - | 6 | 11 |
| Sugerir | - | - | - | 3 | - | 1 | 4 | 4 |
| Convidar | - | - | - | - | - | - | 0 | 11 |
| Apoiar | - | - | - | - | - | - | 0 | 12 |
Desafiar e Guiar destacam-se como as ações mais focadas no raciocínio. Na ação de Desafiar há um claro predomínio de características ligadas ao raciocínio: só num caso é que a professora lança um desafio que não lhe está associado. É também na ação de Desafiar que se identificam quase todas as questões da professora com características não diretamente relacionadas com processos de raciocínio específicos (Meta-analisar), como acontece quando Leonor desafia os alunos a analisar as condições do problema, as estratégias usadas ou o que significa testar uma conjetura.
Ao contrário do que acontece com Desafiar, a maioria das ações de Guiar (35 em 49) não incidem diretamente no raciocínio matemático. Guiar envolve levar os alunos a esclarecer, explicitar ou justificar algo, seja a escolha de um exemplo, o significado de uma expressão, a explicitação de justificações, generalizações e conjeturas ou a opção por uma estratégia de resolução. Guiar tem ainda características de desafiar em diferido, quando se concretiza via um pedido de explicitação de um desafio colocado pela professora a um ou vários grupos, na fase de exploração autónoma da tarefa.
Informar assume a forma de uma afirmação ou esclarecimento que visa descrever ou recordar um determinado caminho de exploração da tarefa, salientar ou validar uma ideia, relacionada ou não com o raciocínio matemático. Assim, pode ter características associadas aos processos de raciocínio, revelando-se como a ação em que o professor inclui aspetos importantes destes processos, concretizando-os para a tarefa em discussão.
A ação de Sugerir assume a forma de um comentário ou recomendação e envolve a análise de explicações ou justificações e a apreciação crítica de uma estratégia, podendo ou não focar o raciocínio matemático. Distingue-se da ação de Informar por visar diretamente a participação do aluno.
Ao Convidar podem ou não estar subjacentes aspetos relacionados com Matemática uma vez que a organização das intervenções dos alunos pode assentar no conhecimento que o professor tem das conclusões a que chegou durante o trabalho autónomo ou das características das suas participações habituais. As “ações de Convidar que têm subjacente uma intenção relacionada com a Matemática” estão muito associadas ao início de segmentos de discussão coletiva, em que se solicita a alunos ou grupos que apresentem o que fizeram, evidenciando-se um planeamento da sequência de apresentações baseado no trabalho por eles previamente realizado. Podem, igualmente, ocorrer na sequência de um momento de discussão em que a professora parece sentir importante introduzir um contributo com determinadas características. Convidar pode estar associado à explicitação de processos de raciocínio, embora esta relação não tenha sido identificada na análise efetuada.
Apoiar é uma ação que se distingue de Guiar uma vez que corresponde a enfatizar uma opção, uma resposta ou observação dos alunos, sem ter a intenção de lhes solicitar alguma resposta, mas que visa encorajá-los a prosseguir a apresentação de uma ideia ou argumentação.
CARACTERÍSTICAS DAS AÇÕES ASSOCIADAS AO RACIOCÍNIO MATEMÁTICO
A análise de dados permite destacar uma categoria de processos matemáticos que designamos por Meta-analisar, não associada a um determinado processo de raciocínio, mas claramente focada no raciocínio matemático. Esta categoría é identificada, sobretudo, na ação de Desafiar, mas também ocorre em Sugerir. Envolve a reflexão sobre estratégias gerais de resolver um problema ou de con-duzir uma investigação matemática (Quadro 8).
Quadro 8. Características das ações focadas em processos Meta-analisar.
Desafiar os alunos a:
- analisar as condições do problema e perceber o que o resultado de um determinado teste implicaria para as condições iniciais do problema;
- identificar diferenças entre resoluções da tarefa, explicando-as e/ou explicitando como poderiam modificar a estratégia que usaram inicialmente;
- associar o procedimento que usaram ao de formular e testar conjeturas.
Sugerir uma estratégia para produzir e testar uma conjetura.
As ações da professora associadas a Justificar (Quadro 9) centram-se, no caso da tarefa analisada, na justificação de porque é que alguns exemplos ‘funcionam’ e outros não e na fundamentação dos exemplos usados.
Associado a Generalizar (Quadro 10) salientamos o desafio para reformular ou avançar com uma generalização e a sugestão de análise de um padrão.
Quadro 10. Características das ações focadas em Generalizar.
Desafiar os alunos a reformular e/ou estabelecer uma generalização.
Guiar os alunos a formular uma característica geral comum a todas as soluções.
Informar, validando, uma ideia baseada no que os alunos fizeram ou disseram indicada pelos alunos.
Sugerir a hipótese de haver ‘algo’ por detrás da generalização avançada pelos alunos.
As ações da professora focadas em Exemplificar (Quadro 11) visam a análise crítica do uso de exemplos, quer provocando instabilidade sobre se eles podem ou não ser considerados exemplos, quer procurando a explicitação de mais exemplos e o seu uso para avançar na resolução do problema. Este último aspeto é fundamental pois é nele que reside a essência de considerar a exemplificação como um processo (auxiliar) de raciocínio.
Quadro 11. Características das ações focadas em Exemplificar.
Desafiar os alunos
- provocando uma instabilidade relativamente à justificação dos exemplos analisados;
- procurando que explicitem outros exemplos.
Guiar os alunos a concretizar o uso de exemplos que foram testados.
Informar que não há só um exemplo que satisfaz as condições do enunciado.
A tarefa analisada ilustra como focar a atenção no tipo de números que obedecem a uma ou mais condições é uma ação que pode levar os alunos a Classificar (Quadro 12).
Finalmente, conjeturar (Quadro 13), embora seja um processo de raciocínio pouco presente na discussão coletiva, é um processo para o qual a professora consegue guiar os alunos.
RELAÇÕES ENTRE AÇÕES E PROCESSOS DE RACIOCÍNIO
As características das ações identificadas têm diferentes níveis de generalidade, com as mais específicas, naturalmente, muito associadas à tarefa discutida com os alunos. No entanto, sugerem um menu de características que o professor pode ter em conta na preparação da discussão coletiva.
Na Figura 3 apresentamos um modelo com génese no proposto por Ponte et al. (2013) e Mata-Pereira e Ponte (2017, 2018a, 2018b), que traduz as relações e ações observadas e que reflete (i) a individualização de ações que possuem características próprias, tal como fundamentado anteriormente, (ii) as potencialidades de cada tipo de ação para desenvolver o raciocínio matemático, e (iii) a inter-relação e sequencialidade das ações.
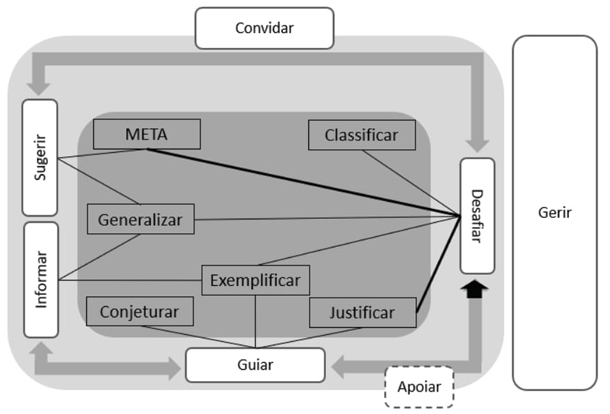
Figura 3 Modelo das ações da professora na condução de discussões coletivas que pro-movem o raciocínio matemático.
A parte mais sombreada destaca as relações entre as ações do professor e o foco no raciocínio matemático. As ligações ‘diretas’ entre cada ação e os diferentes processos de raciocínio traduzem os dados analisados e permitem assinalar as potencialidades identificadas. Desafiar é a ação mais associada ao raciocínio matemático, incidindo diretamente sobre Classificar, Justificar, Exemplificar, Generalizar e sobre os processos Meta-analisar, associados à análise de estratégias gerais de resolução de problemas e de exploração de investigações matemáticas. As ligações mais ‘grossas’ traduzem a maior incidência nos processos Justificar e Meta-analisar.
A parte mais escura da seta dupla que liga Guiar a Desafiar traduz uma característica importante da ação de Guiar, quando assume a forma de desafio em diferido, em que a professora solicita que os alunos explicitem desafios que colocou durante a fase de exploração da tarefa em pequenos grupos.
Não foi identificada nenhuma ação de Convidar ou Apoiar que incidisse diretamente sobre o raciocínio matemático. No entanto, é possível que isso aconteça quando, por exemplo, se seleciona um aluno ou grupo a participar, ou se enfatiza o que disseram, tendo como critério, um exemplo, uma justificação, uma classificação que a professora identificou durante a exploração autónoma da tarefa. Por isso, no modelo da Figura 3 estas ações estão parcialmente incluídas na parte sombreada mais clara. Apoiar está colocado entre Guiar e Desafiar, evidenciando a interligação e sequencialidade identificadas: (1) começar por Apoiar validando o que os alunos disseram e solicitando de seguida que precisem aspetos ligados ao que estavam a apresentar (Guiar) e (2) começar por Apoiar antes de Desafiar os alunos.
O modelo apresentado avança seis categorias para as ações do professor durante a discussão coletiva, diretamente relacionadas com tópicos e processos matemáticos, explicita as suas relações com o raciocínio matemático e salienta a interligação entre elas. A opção de análise foi focar cada ação e não sequências de ações. No entanto, uma vez que a sequencialidade entre Apoiar e Guiar e Apoiar e Desafiar se evidenciou, ela é igualmente assinalada no modelo.
CONSIDERAÇÕES FINAIS
O modelo das ações do professor na condução de discussões coletivas que promovem o raciocínio matemático que propomos (Figura 3), evidencia, tal como o de Ponte et al. (2013) e Mata-Pereira e Ponte (2017, 2018a, 2018b), a importância das ações do professor para que nas discussões coletivas possa emergir o raciocínio matemático. Avança, ainda, com a especificação das potencialidades de cada um dos tipos de ações para promover os processos de raciocínio matemático considerados.
Este estudo, embora focando cada tipo de ação do professor per si, identifica a inter-relação entre ações de Apoiar e Guiar e um sentido de Guiar associado a Desafiar, Desafiar em diferido. Estes resultados estão na linha do que Cengiz et al. (2011) afirmam sobre a combinação de sequências de ações para efetivamente desenvolver o pensamento dos alunos e sugerem, igualmente, a pertinência de desenvolver um modelo que possa incluir o impacto de um conjunto de ações e não apenas o de ações isoladas.
Identificamos um processo de raciocínio não referido na literatura, Meta-analisar, que corresponde a um nível de pensamento em que os objetos são os processos de raciocínio e sobre o qual importa que o professor foque algumas das suas ações. Meta-analisar corresponde a fazer uma abstração e pensar sobre características, por exemplo, de conjeturar ou generalizar.
Reconhecemos potencialidades do modelo das ações do professor na condução de discussões coletivas que promovem o raciocínio matemático (Figura 3) e das características das ações do professor identificadas, nomeadamente na fase de planificação quando o professor prepara as questões que pode colocar aos alunos e antecipa os processos e representações que eles poderão usar. No entanto, esta será uma vertente que importa aprofundar em futuras investigações. Finalmente, salientamos que o modelo proposto é hipotético e necessita ser precisado em futuros estudos que incidam na análise da exploração de outras tarefas, focadas no desenvolvimento do raciocínio matemático, conduzidas por diferentes professores.











 text new page (beta)
text new page (beta)





