1. INTRODUCCIÓN
El razonamiento covariacional es un constructo teórico ampliamente utilizado dentro de un creciente cuerpo de investigación centrado en explicar el desarrollo cognitivo relativo a la coordinación de cantidades que varían simultáneamente (Carlson, Jacobs, Coe, Larsen, y Hsu, 2002; Saldanha y Thompson, 1998; Thompson y Carlson, 2017). El razonamiento covariacional son las actividades cognitivas involucradas en la coordinación de dos cantidades variables mientras se atiende la relación de las formas en que ambas cambian (Carlson et al., 2002, p. 357). Razonar covariacionalmente implica realizar acciones mentales, en diferentes niveles de desarrollo, involucradas en la concepción acerca de la variación de dos cantidades que varían.
Se ha demostrado que el razonamiento covariacional es fundamental para que los alumnos comprendan numerosos conceptos matemáticos en nivel bachillerato y superior; como son las relaciones exponenciales (Castillo-Garsow, 2010; Confrey y Smith, 1995; Ellis, Ozgur, Kulow, Dogan, y Amidon, 2016; Ellis, Ozgur, Kulow, Williams, y Amidon, 2012; Ferrari-Escolá, Martínez-Sierra, y Méndez-Guevara, 2016), las funciones trigonométricas (Moore, 2010, 2012, 2014)K. C. (2010), la razón de cambio (Johnson, 2012, 2015a, 2015b), el concepto de función (Carlson et al., 2002; Johnson, 2012, 2015a, 2015b), el teorema fundamental del cálculo (Thompson, 1994b), gráficos de funciones (Carlson et al., 2002; Moore, Paoletti, y Musgrave, 2013) y ecuaciones diferenciales (Castillo-Garsow, 2010).
El razonamiento covariacional es considerado como una forma fundamental del razonamiento matemático de los estudiantes, que es utilizado cuando aprenden el concepto de función (Johnson, McClintock y Hornbein, 2017). Existen dos perspectivas de covariación: una estática y otra dinámica. De manera general, desde la perspectiva estática, las cantidades de una variable se asocian con las cantidades de otra variable; en tanto que, desde la perspectiva dinámica, los cambios en una variable están asociados con cambios en otra variable (Johnson, 2012).
Particularmente, Confrey y Smith (1994)
proporcionan una perspectiva de covariación estática de una función cuando se toma
como una yuxtaposición de dos progresiones, cada una generada independientemente a
través de patrones de datos, evidencia que emerge de su estudio sobre la función
exponencial. En tanto que Carlson et
al. (2002) trabajan desde una perspectiva dinámica que parte
de interpretar y representar modelos gráficos, entre otros, el llenado de
recipientes. Referente a la función exponencial, Ferrari-Escolá, et al. (2016), resaltan dos formas de
aproximarse a dicha función. La primera aproximación hace referencia al trabajo de
Thompson (2008), Ellis et al (2012), y Castillo-Garsow (2010) sobre razón de cambio, donde se considera
que la tasa proporcional en la cual una función cambia con respecto al valor de la
función, en un determinado instante, es una característica que define a las
exponenciales. Es decir, ∀x ∈ ℜ, f(x) es una función exponencial si existe h ∈ ℜ,
tal
La segunda forma de aproximación reconoce que la función exponencial puede ser vista como la yuxtaposición de dos progresiones, cada una de ellas construida de manera independiente (Figura 1) a través de análisis numéricos e identificación de patrones (Confrey y Smith, 1994). En un sentido formal, la construcción de una función exponencial es la construcción de un isomorfismo entre los mundos de contar (aditivo) y multiplicar (multiplicativo) a través de la covariación.
A partir de la segunda aproximación podemos pensar en construir la función loga-ritmo y la función exponencial desde el mismo razonamiento covariacional, el cual surge al considerar ambas funciones como la yuxtaposición de dos progresiones una aritmética y otra geométrica, bajo la misma mirada de Napier y Briggs que, a principios del siglo XVII, buscaban una herramienta para facilitar cálculos; en tanto que Newton, Huygens y Agnesi, a finales del mismo siglo, se enfocan en describir fenómenos que involucran continuidad (Ferrari y Farfán, 2010).
El propósito de esta investigación es indagar el desarrollo del razonamiento covariacional logarítmico-exponencial en futuros profesores de matemáticas desde una perspectiva estática de covariación hacia una perspectiva dinámica mediante la construcción geométrica de puntos con el software GeoGebra, el uso de tablas y hojas de cálculo, así como la graficación o ajuste de puntos que involucra un acercamiento a la continuidad de la función.
2. MARCO TEÓRICO
De acuerdo con Carlson et al. (2002), el razonamiento covariacional es entendido como las actividades cognitivas individuales involucradas para coordinar la variación simultánea de dos cantidades al reflexionar sobre la variación que existe entre ambas. Señalan que, si se quiere determinar la capacidad que tiene un individuo de razonar covariacionalmente, se deben analizar, en conjunto, los comportamientos y las acciones mentales (AM) exhibidos al responder tareas específicas de covariación. Para estos investigadores, un estudiante logra cierto nivel de razonamiento covariacional de acuerdo con la imagen global que apoya las diversas acciones mentales exhibidas durante las tareas de covariación. En su marco conceptual de razonamiento covariacional consideran cinco niveles de desarrollo. Señalan que la habilidad de razonar covariacionalmente alcanza un nivel de desarrollo cuando mantiene las acciones mentales asocia-das a los niveles inferiores. La imagen que describe los niveles es caracterizada por Thompson (1994a), como aquello que se enfoca en la dinámica de las operaciones mentales. Es importante mencionar que el razonamiento covariacional es más sofisticado a medida que la imagen se va desarrollando.
En ese sentido Ferrari-Escolá et al. (2016) proponen una reformulación (Tabla 1) de los niveles de desarrollo del razonamiento covariacional descritos por Carlson et al. (2002), pues el objetivo de su investigación fue identificar el razo-namiento covariacional logarítmico-exponencial de estudiantes de bachillerato desde un acercamiento discreto hacia un análisis continuo de la función loga-rítmica. Reformulación que utilizamos para nuestra investigación como marco conceptual.
Las acciones mentales y su entrelace en niveles de razonamiento covariacional emergen del estudio epistemológico reportado por Ferrari (2008), en don-de se identificaron elementos esenciales que, consideramos, caracterizan la covariación logarítmica-exponencial. Percibimos allí que construir progresiones (una aritmética, otra geométrica), reconocer y vincular las operaciones aritméticas involucradas, así como la convención matemática (loga1 = 0; a > 0, a ≠ 1) surge para generar un sistema logarítmico facilitador de cálculos, en tanto que en la exponencial (a0 = 1, a > 0) para extender la estructura algebraica más allá de los números naturales.
Tabla 1 Razonamiento covariacional logarítmico-exponencial
| Nivel 1 | Nivel 2 | Nivel 3 | Nivel 4 | Nivel 5 | |||||
|---|---|---|---|---|---|---|---|---|---|
| AM1.Coordinación entre los números. Reconocer orden y secuencia en cada progresión. | Se percibe cuando se trabaja con los elementos de construcción de los puntos y se reconoce el orden de los elementos de las progresiones. | Implica reflexionar sobre AM1 e incorporar AM2 mientras se trabaja en cómo cambian las cantidades involucradas. | Articular AM1, AM2 y AM3, propician la internalización y coordinación de las operaciones involucradas, mientras se piensa en el conjunto de números y operaciones, sin aún coordinar las progresiones. | Incorporar AM4 refuerza el nivel anterior al reconocer nuevas acciones y propiedades sobre objetos a través de la construcción de nuevos puntos de la curva. | Coordinar las acciones mentales anteriores con AM5, promueve internalizar y coordinar acciones sobre progresiones y operaciones aritméticas que conducen a la covariación logarítmica-exponencial. | ||||
| AM2. Coordinación de la dirección de la cantidad del cambio en cada progresión numérica. Identificar si la progresión aumenta o disminuye al reconocer operaciones aritméticas entre números y, por lo tanto, el cambio aritmético (diferencia) y el cambio geométrico (cociente). | |||||||||
| AM3. Coordinación de las operaciones aritméticas que generan las progresiones. Esto implica la asociación de la multiplicación con la suma como la operación que permite la construcción de puntos de la curva. | |||||||||
| AM4. Coordinación de las operaciones que completan las progresiones numéricas al extender el conjunto de números naturales al racional, y el conjunto de números racionales al real, para obtener la reversibilidad de las operaciones. | |||||||||
| AM5. Coordinación de las progresiones. Implica relacionar una coordenada de un punto con la otra coordenada del mismo punto, es decir, abstraer la relación funcional de forma numérica, gráfica o analítica (fórmula o expresión algebraica). | |||||||||
Tomado de Ferrari-Escolá et al., 2016.
3.- METODOLOGÍA
Dada la complejidad de los contextos de enseñanza/aprendizaje y la necesidad de una metodología sensible a ellos, consideramos adecuada para nuestra investigación sobre desarrollo del razonamiento covariacional logarítmico-exponencial la metodología de investigación basada en diseño. Según Molina, Castro, Molina y Castro (2011) es una metodología cualitativa que “persigue comprender y mejorar la realidad educativa a través de la consideración de contextos naturales en toda su complejidad, y del desarrollo y análisis paralelo de un diseño instruccional específico” (p.75). Para Molina et al. (2011) el objetivo de esta metodología es “analizar el aprendizaje en contexto mediante el diseño y estudio sistemático de formas particulares de aprendizaje, estrategias y herramientas de enseñanza, de una forma sensible a la naturaleza sistémica del aprendizaje, la enseñanza y la evaluación” (p. 76).
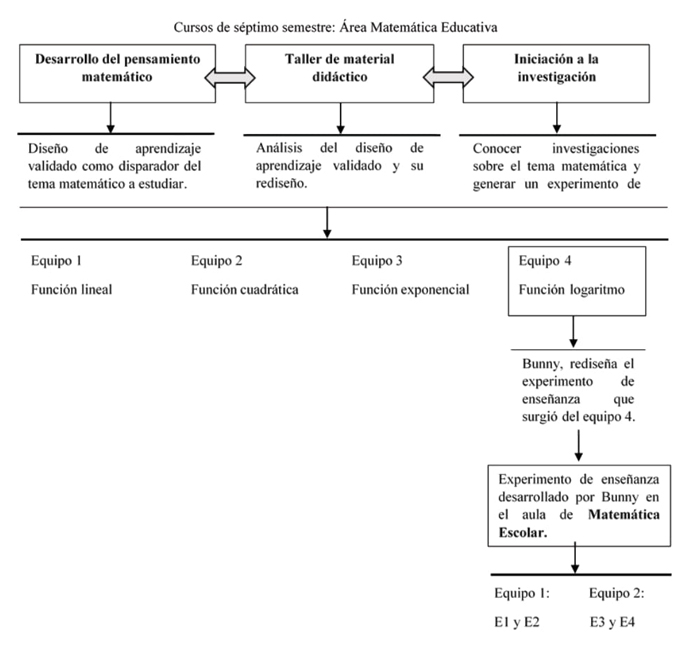
Como parte de nuestra investigación, trabajamos tres cursos con 16 estudiantes del séptimo semestre de la licenciatura en Matemáticas con especialidad en Matemática Educativa de la Facultad de Matemáticas de la Universidad Autónoma de Guerrero (UAGro), México. Los cursos fueron: (1) Desarrollo del pensamiento matemático, donde se profundizarían temas matemáticos iniciados con diseños de aprendizaje validados en otras investigaciones; (2) Taller de material didáctico, donde se analizaría y discutiría el diseño de aprendizaje que se había desarrollado en el curso 1, mismo que rediseñarían creando un nuevo diseño de aprendizaje, y, (3) Iniciación a la investigación, donde aprenderían a realizar un estado de arte y articular los elementos trabajados en los otros dos cursos para diseñar un experimento de enseñanza y ponerlo en escena.
Dentro de la metodología de investigación basada en diseño se enmarca el “experimento de enseñanza”, considerado como una secuencia de episodios de enseñanza diseñados por un investigador. En este experimento participan uno o más estudiantes y un testigo (otro investigador o el profesor del curso), y se determina un método de recolección de datos. Los datos son utilizados para rediseñar episodios siguientes y realizar análisis retrospectivo del experimento de enseñanza desarrollado (Steffe y Thompson, 2000).
Los 16 estudiantes, futuros profesores de matemáticas, fueron organizados en cuatro equipos de cuatro integrantes designándoles un tema matemático para investigar. Se les invitó a trabajar sobre función lineal y función cuadrática (cuyos diseños de aprendizaje fueron tomados de Méndez, 2013); así como sobre función exponencial y función logarítmica (cuyos diseños de aprendizaje fueron tomados de Ferrari, 2008). Todos los equipos entregaron, al finalizar su séptimo semestre, un trabajo final reportando su análisis del experimento de enseñanza que desarrollaron con estudiantes de la facultad (Esquema 1), el cual no se reportan en el presente artículo.
En este artículo nos centramos en el análisis de las producciones de los participantes del experimento de enseñanza sobre función logarítmica diseñado por Bunny (pseudónimo), integrante del Equipo 4, quien cursaba el octavo semestre. Bunny desarrolla su experimento de enseñanza en el curso Matemática Escolar con estudiantes de sexto semestre de la facultad. Bunny se encontraba desarrollando su trabajo de tesis de licenciatura enfocado a los logaritmos en coordenadas polares, había tomado 90% de los cursos de la licenciatura en matemáticas y del área de matemática educativa. Había participado en congresos nacionales e internacionales referentes al ámbito educativo donde colaboró en el desarrollo de distintos talleres o laboratorios, ponencias y carteles referentes a covariación logarítmica-exponencial. Su trayectoria académica nos motivó a invitarlo a esta investigación sobre formación inicial y covariación, de la cual se desprende el presente escrito.
El objetivo de la investigación es contribuir a la literatura que indaga acerca de cómo lograr el desarrollo del razonamiento covariacional a través de contestar la pregunta: ¿Qué niveles de razonamiento covariacional logarítmico-exponencial se perciben en futuros profesores de matemáticas de sexto semestre de licenciatura? En particular, en esta investigación, indagamos el desarrollo del razonamiento covariacional logarítmico-exponencial en futuros profesores de matemáticas, provocado por un experimento de enseñanza basado en la construcción geométrica de puntos de una curva logarítmica, según la construcción geométrica de puntos que aporta Descartes en su obra de Geometría (1630) que Confrey y Dennis (1997) analizan en su artículo.
Así, la contribución de nuestra investigación es dar evidencia empírica de cómo el experimento de enseñanza fomenta el desarrollo del razonamiento covariacional logarítmico-exponencial, según la reformulación de Ferrari-Escola, Martinez-Sierra y Mendez-Guevara (2016).
3.1. Participantes y recolección de datos
En el experimento de enseñanza participaron cuatro jóvenes de entre 22 y 24 años, tres hombres y una mujer, inscritos en el curso Matemática Escolar de sexto semestre del área de Matemática Educativa de la Facultad de Matemáticas de la UAGro. Dentro de la trayectoria escolar de los participantes encontramos asignaturas de formación básica como: Álgebra lineal (I al III), Geometría, Geometría Analítica (I y II), Cálculo (I al IV), Análisis Numérico, entre otras. Su formación de especialidad en matemática educativa marca como asignaturas cursadas al momento de su participación: Tecnologías en la Matemática Educativa, Historia de las Matemáticas, Fundamentos de la Educación, Análisis del Sistema Educativo, Metodología de la Enseñanza, por mencionar algunas.
Los cuatro participantes fueron distribuidos en dos equipos (Equipo 1 y Equipo 2), de dos integrantes cada uno. Las tareas se desarrollaron como parte del curso en dos sesiones, cada una de 100 minutos.
En las dos sesiones se trabajó sobre logaritmos, iniciándose con la construcción geométrica de una curva logarítmica utilizando GeoGebra. Estas sesiones se desarrollaron en el laboratorio de modelación de la Facultad de Matemáticas en Acapulco. El equipo de investigación estuvo integrado por: Bunny, que desarrollaría las sesiones, testigos encargados de tomar notas de campo (autores de este artículo) y dos auxiliares que videograbaron las sesiones.
Para la toma de datos se contó con tres videocámaras, dos de ellas se ocuparon para grabar la actividad de los dos equipos participantes, la tercer videocámara estuvo a cargo de un testigo, con la resposabilidad de grabar la actividad general del salón de clases. De igual manera, se registraron las grabaciones de pantalla desde los equipos de cómputo utilizados para evidenciar el trabajo realizado en el software. También se recabaron, al término de cada sesión, los archivos “.ggb” generados en GeoGebra. Se rescataron los archivos de audio de cada sesión, así como las hojas de trabajo de los estudiantes y las notas de campo de los testigos.
Se presentan en este escrito, luego del análisis de los datos obtenidos, algunos elementos sobre las acciones mentales y los niveles de razonamiento covariacional logarítmico-exponencial percibidos en dos estudiantes del Equipo 1 (E1 y E2) mientras desarrollan las tareas en el experimento de enseñanza.
3.2. Tareas
El sustento del diseño de las tareas descansa en el estudio epistemológico reportado por Ferrari (2008) respecto a logaritmos donde se destaca la importancia, que en siglos pasados, se otorgaba a las construcciones geométricas dentro del estudio de las variaciones y el cambio. En el mismo sentido Dennis y Confrey (1997) rescatan de la obra de Descartes, la construcción geométrica de puntos en un plano propiciando la asociación de las coordenadas con su variación, es decir, favoreciendo argumentos covariacionales. En el diseño de las tareas involucramos la geometría dinámica en la construcción de una curva logarítmica con el uso de un círculo unitario; de ciertas rectas tangentes y secantes; así como también, la semejanza de triángulos. Elementos que fueron trabajados en el curso de Desarrollo del Pensamiento Matemático y que fueron reproducidos en el experimento de enseñanza con pequeños retoques persona-les del estudiante Bunny.
De esta manera, el diseño del experimento de enseñanza estuvo constituido por dos actividades que se encaminan hacia la construcción geométrica de puntos pertenecientes a la función logaritmo base 2, para lo cual se utilizó GeoGebra. La dinámica de clase implementada por Bunny fue la siguiente:
1. Iniciar la sesión con las instrucciones de trabajo para guiar a los estudian-tes en la construcción geométrica de puntos de la curva (Figura 2):
Particionar el eje y: y 0 =0; y 1 =0.5; y 2 =1: y 3 =1.5; y 4 =2
Insertar una circunferencia unitaria cuyo centro sea el origen del sistema de coordenadas cartesianas y la cual determina el punto x 0 = (1,0).
Trazar una línea recta (s) que pase por el origen y un punto A (cualesquiera) de la circunferencia logrando un ángulo de incli-nación de 45 grados (Figura 2-a).
Trazar una recta tangente a la circunferencia por el punto A y determinar x 1 (Figura 2-b).
Trazar una recta vertical por x 1 y una recta horizontal por y 1 y determinar el punto P1 (Figura 2-c).
Dar tiempo a los participantes para construir más puntos de manera independiente; analizar variaciones en datos e intentar ajustar la curva; identificar las variables en juego y su comportamiento “variacional”; percibir la covariación existente y ajustar una curva a dichos puntos; tareas que serían orientadas mediante preguntas preparadas para incentivar la discusión (Tabla 2);
Tabla 2 Preguntas guía del diseño de aprendizaje
| Número de pregunta | Preguntas | Consideraciones |
|---|---|---|
| 1.1 | ¿Qué forma creen que tiene la curva que pasa por todos los puntos construidos? Dibujarla y explicar sus ideas. | Se espera que los estudiantes realicen un primer esbozo de la curva, sin ser exactos, ya que sólo se consideran pun-tos en el primer cuadrante del plano. Esto los llevaría a percibir la forma de la curva e imaginarla continúa. |
| 1.2 | ¿Cómo se comportan los puntos construidos de la curva?” | Se espera una descripción en base a la observación de puntos, como por ejemplo, son crecientes, decrecientes, están ubicados en cierto cuadrante, etc. que daría indicios de AM1 y AM2 |
| 1.3 | ¿Cuánto cambian las Variables involucradas?” | Se espera que reconozcan, en primer lugar, las variables en juego, y luego trabajen con el comportamiento numérico, para poder determinar los patrones de crecimiento de las dos progresiones en juego. Evidenciarían mayor uso de AM1 y AM2, fortaleciendo tácitamente los niveles 1 y 2. |
| 1.4 | ¿Consideran que el punto “B” pertenece a la curva? ¿Por qué? | Se espera que reconozcan un punto especial de la curva B= (1, 0), el cual les permitiría explorar o reconocer algunas características importantes de la función en juego y quizás estabilizar AM3. |
| 1.5 | ¿Se pueden encontrar puntos de la curva a la izquierda del punto «B»? Expliquen por qué y de ser necesario den ejemplos | Se espera que esta pregunta ayude a romper esquemas que pudieran haber sido establecidos referente al tipo de función que se está trabajando, ya que con la ubicación de más puntos se hacen visibles la asíntota de la función logaritmo base 2. Exige también esta tarea la reversibilidad (AM4) |
| 1.6 | ¿Cómo ajustar los puntos? Es decir, lograr una curva que pase por todos ellos ¿cuál será?” | Se espera que con el análisis cuantitativo desarrollado en la pregunta 3 y las características visuales encontradas en las preguntas 4 y 5, identifiquen la covariación de ambas progresiones en juego, y así identifiquen la covariación logarítmica-exponencial inmersa y enunciar la curva logaritmo en base 2, lo cual evidenciaría la AM5. |
3.3. Análisis de datos
El análisis de los datos se realizó de manera retrospectiva lo cual nos permitió reflexionar sobre los datos obtenidos durante todo el experimento de enseñanza (Molina, et al. 2011). Consideramos que las herramientas teóricas y metodológicas de la investigación están estrechamente ligadas a la pregunta/problema de investigación. De hecho, nuestro proceder teórico, metodológico y analítico es análogo a muchas investigaciones en el campo de investigación acerca del razonamiento covariacional (e.g. Moore, 2013, 2014). La particularidad de nuestra investigación es la reformulación de (Ferrari-Escola, Martinez-Sierra y Mendez-Guevara, 2016) para el desarrollo del razonamiento covariacional logarítmico-exponencial.
Se inició el análisis de los datos mediante el proceso de familiarización, a través de mirar, en repetidas ocasiones, los vídeos recabados, incluso se realizó una mejora en el audio eliminando ruido de las grabaciones mediante las herramientas proporcionadas por el software Audacity ®. Seguido de ello se realizó la transcripción de las grabaciones de vídeo; se revisaron y digitalizaron las hojas de trabajo resultantes de las sesiones; se revisó la construcción hecha en GeoGebra y la grabación de la pantalla recabada, todos estos elementos nos ayududaron a entender, de mejor manera, cómo fueron elaborados cada uno de los elementos geométricos de la construcción en GeoGebra. Cabe mencionar que los estudiantes involucrados presentaban un nivel básico en el uso del software lo cual implicó mantener la configuración predeterminada en aspectos como: ejes, cuadrícula, vistas algebraica y gráfica, así como el uso de dos cifras decimales. Este último aspecto jugó un papel importante durante el análisis de las variaciones realizada por los estudiantes. Para analizar los datos nos apoyamos en el marco conceptual de covariación logarítmico-exponencial expuesto en Ferrari-Escolá, et al. (2016), así como no perder de vista el objetivo propuesto, por lo que utilizamos el análisis continuo (Molina, et al. 2011) al final de cada sesión, que nos permitió tomar decisiones y reorientar el trabajo de ser necesario. Con las transcripciones completas los autores identifican, por separado, momentos donde se vislumbran en los estudiantes aspectos covariacionales o elementos relacionados al crecimiento, o variación de las variables en juego, para luego triangular y validar los episodios seleccionados como evidencia de las acciones mentales y los niveles de razonamiento covariacional percibidos en la primera sesión del experimento de enseñanza.
4. RESULTADOS
El experimento de enseñanza inicia con la explicación de Bunny para la construcción de dos puntos (P1 y P2) de la curva a analizar. Esta actividad tuvo una duración aproximada de 23 minutos, debido a que fue necesario instruir a los estudiantes en las herramientas de GeoGebra que se utilizarían. Después de la construcción de los primeros dos puntos, se les solicita construir más pun-tos y analizarlos hasta lograr reconocer la curva; con tantos puntos como consideraran necesarios.
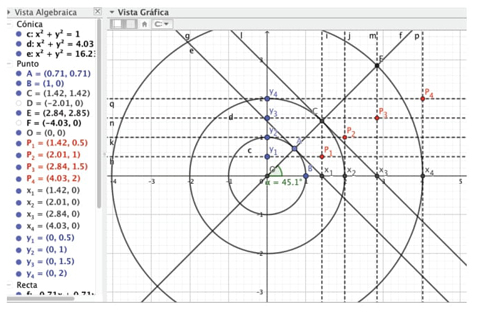
El Equipo 1, inicia construyendo los puntos P1= (1.42, 0.5) y P2= (2.01, 1) con cierta imprecisión, debido a que no han ajustado la inclinación de la recta inicial a 45o como se les solicita en la actividad (Figura 2-a), y eso les perturba para analizar numéricamente el crecimiento de los puntos.
Luego de las explicaciones de Bunny y la construcción de los dos primeros puntos, E1 y E2 acuerdan construir dos puntos más (P3 y P4), utilizando aproximadamente 5 minutos en esa tarea (Figura 3).
4.1. Episodio 1: Los puntos se van “anchando” de manera creciente
Con los cuatro puntos construidos los estudiantes inician la búsqueda de patrones de crecimiento (Extracto 1) y como primera herramienta toman diferencias entre ordenadas consecutivas (Extracto 1, Línea 029). Reconocen que deben encontrar la variación de las coordenadas de los puntos construidos. E2 menciona: “¿cuánto van variando?, o ¿no crees que van variando?” (Extracto 1, Línea refiriéndose a las abscisas luego de que E1 señala que los valores de “y” tienen un aumento constante de 0.5 en 0.5 (Extracto 1, Línea 023). Se observa que los estudiantes logran identificar las dos variables en juego, pero solo explicitan la manera de variar las ordenadas “y”, cuya construcción se deriva de la partición solicitada. El reto mayor es determinar cómo varían los valores de “x” que emergen de la construcción geométrica propuesta, ya que buscan una regularidad en la diferencia de dos valores consecutivos.
Extracto 1 Diferencia entre valores de x
| Línea | Participación | Figura | |
| 022 | E2: | x1, la distancia que hay de… |
|
| 023 | E1: | 1.42… bueno nada más con estos puntos; estos son los que hice… los de las “y” nada más van aumentando punto 5. | |
| 024 | E2: | ¿Y los de “x”?... ¿ Calculadora? | |
| 025 | E1: | ¿Para qué? | |
| 026 | E2: | Para ver cuánto van variando, ¿o no crees que van variando? | |
| 027 | E1: | Sí van variando aquí son 51 o 52, acá no? ENT[refiriéndose a la distancia entre las abscisas de P1 y P2ENT] Este de acá son 83 ENT[indicando a la distancia entre las abscisas de P3 y P4ENT]. | |
| 028 | E2: | 0.59 ENT[usa la calculadora para la distancia entre las abscisas de P1 y P2ENT]. | |
| 029 | E1: | El otro es 4.03 - 2.84 son… | |
| 030 | E2: | 59, 83 y 1.19 ENT[anotando en su hoja de trabajoENT]. |
Hasta ese momento los estudiantes han percibido que las variables van en aumento y que para “y” son de 0.5 en 0.5, mientras que siguen buscando determinar la variación de “x” mediante diferencias. El trabajo no los conduce hacia algo concreto, sin embargo, mediante la observación de los puntos construidos, conjeturan que se trata de un “parábola”, debido a que consideran que el gráfico “debería ser simétrico”. Incluso a la hora de graficar la curva en la hoja de trabajo, su trazo inicia en el origen y generan una curva que va creciendo con la concavidad hacia arriba (Figura 4).
Observamos entonces que los estudiantes identifican qué varía, pero, no logran aún determinar cuánto varía, al menos no para los valores de “x”, sólo visualizan que ambas variables crecen. Discuten sobre si se trata de un crecimiento cuadrático (E1) o exponencial-logarítmico (E2), sin llegar a una conclusión conjunta para definir cómo varía el crecimiento de los puntos.
En este episodio evidenciamos cómo se perciben indicios de AM1 y AM2 en las discusiones y trabajo de los estudiantes, debido a que logran identificar las dos variables en juego y que ambas crecen. Los comportamientos exhibidos por estos estudiantes al responder la tarea fueron indicios de los niveles de coordinación y de dirección (Nivel 1 y Nivel 2). Buscan también, de manera cuantitativa, la variación de una de ellas (la variable “x”) sin lograr aún el patrón de crecimiento, mientras que para la segunda variable (“y”) observan que es creciente de manera directa por la partición indicada en la tarea, por tanto, conocen cuánto varía. Esto induce a los estudiantes a percibir que los puntos construidos se van “anchando” de manera creciente, como lo comenta E2 a su compañero, lo que implícitamente involucra el hecho de que la razón de cambio va siendo cada vez más pequeña.
4.2. Episodio 2: Para valores naturales podemos sumar 1 y duplicar
Los estudiantes llegan a un momento de confusión, su análisis numérico mediante diferencias no les ha permitido identificar la variación de los valores de “x”; en tanto que la parte gráfica los lleva a conjeturar que podría tratarse de una parábola. Bunny interviene para apoyarlos y les hace la observación de que el ángulo de inclinación de la recta S (Figura 2-a) no mide 45º y les solicita ajustar el ángulo. Con ello los puntos construidos se tornan más cómodos, incluso aparecen números naturales como se puede observar en la Figura 5 donde los puntos de la izquierda son los que construyeron primero y los puntos de la derecha son los que obtuvieron después del ajuste del ángulo.
Con los nuevos puntos (extracto 2), reconocen que van apareciendo, primero, un número decimal y después uno entero; aparece un decimal y luego un ente-ro, y así siguiendo en ambas variables. Construyen entonces otro punto (solo la abscisa) utilizando una circunferencia para probar su conjetura de número decimal, entero, decimal, entero y predicen que para el valor 3 de “y” el valor de la coordenada “x” va a ser 8, así determinan el punto P5= (8,3). Los estudiantes reconocen que las ordenadas enteras 1, 2 y 3 están relacionadas con los valores enteros de las abscisas 2, 4 y 8 respectivamente. Es decir, observan el cambio en “x” y el cambio en “y”. Más aún, pudieron determinar que los valores en “x” aumentan al doble (extracto 2, línea 105) y los valores en “y” de uno en uno, fortaleciendo así las AM1 y AM2 parcialmente, ya que no logran aún el patrón general de crecimiento de cada variable en conjunto, esto los mantiene dentro de los primeros dos niveles de razonamiento (coordinación y dirección).
Extracto 2 Va aumentando el doble
| Línea | Participación | |
|---|---|---|
| 097 | E1: | Es que en los puntos 1, 2, 3 en el 1 llega el 2 para x, y= 2 va 4, en y=3 se va al 8 y los decimales en y… esta… tiene decimales en x en los puntos. |
| 098 | Bunny: | ¿Encontraste que aquí es 2, 4, 8? ENT[indicando las abscisasENT]. |
| 099 | E1: | Sí. |
| 100 | Bunny: | El siguiente entonces ¿cuál sería? |
| 101 | E1: | El siguiente va a quedar con decimal, va a tener decimales pues. |
| 102 | Bunny: | ¿Y el siguiente? |
| 103 | E1: | El siguiente sería… ¿Cuál es el siguiente Chavo? pienso que 16, pero sí 16. |
| 104 | Bunny: | 16 ¿Por qué? |
| 105 | E1: | Porque va aumentando, el punto que tenemos es 2, luego el doble sería 4, luego el doble es 8, el doble de 8, 16. |
En este momento, los estudiantes observan que ambas cantidades (valores de x y valores de y) crecen con cierto incremento; el doble en valores enteros de “x” y aumento de 1 en valores enteros de “y”, lo cual podemos identificar como AM1 e inician un acercamiento más robusto de AM2, pese a que no logran incorporar en su discusión los puntos intermedios construidos que involucran números no enteros.
4.3. Episodio 3: Las progresiones
E1 y E2 han determinado que en las coordenadas de los puntos construidos se podían encontrar números decimales o enteros. Para las coordenadas de valor entero descubrieron que se puede ir duplicando los valores de las abscisas y sumar 1 en las ordenadas para obtener el punto siguiente con coordenadas enteras. Sin embargo, aún no han logrado percibir con mayor fineza el patrón de crecimiento de las variables, es decir, solo pueden determinar P2, P4 y P6 dejando los huecos de P1, P3 y P5 que precisamente son puntos cuyas coordenadas son decimales. Para salir de esa encrucijada necesitan el apoyo de Bunny quien los induce a observar que el valor de la abscisa del punto P1 se puede considerar como una aproximación a la raíz cuadrada de dos (extracto 3, línea 165). Con ello reescriben los puntos que han construido (extracto 3, línea 171).
Extracto 3 Reemplazando por raíz de dos
| Línea | Participación | |
|---|---|---|
| 165 | Bunny: | Ajá, las “y” siempre crecen 0.5 en 0.5. Bueno, lo que yo haría primero es poner los puntos que tengo allí, que voy a analizar, que quiero cuantificar, ponerlos aquí más claro ¿no? [refiriéndose a escribirlos en papel]. Digo, también en la pantalla es más complicado poner los “x”, claro. ¿Cuáles son solamente los P? Y quizás ahí encontrar algo, si no funciona la resta, no sale nada uniforme en la resta, ¿qué otra puedo encontrar en la variación? … … … 1.41... ese 1.41 ¿No les evoca nada? ¿No se acuerdan qué número es? |
| 166 | E2: | Esto es raíz cuadrada de 2 [indicando el 1.41 del punto P1 en la lista de puntos que han escrito], esto es raíz cuadrada de 4 [indicando la abscisa del punto P2]. |
| 167 | E1: | Entonces, es como ésta, pero no... |
| 168 | E2: | Así lo dejamos [refiriéndose a la pregunta 4 sobre B=(1,0)]. |
| 169 | E1: | Sí, ya. |
| 170 | E2: | Pero lo podemos tomar como un punto x sub cero. |
| 171 | E1: | Si reemplazamos esto por lo que dijimos hace rato, éste es la raíz de 2, ésta raíz de 4, ésta raíz de 8, raíz de 16, raíz de 32, raíz de 64 y el punto que está aquí es la raíz de 1, es el que tenemos, pues a ver cómo concebimos eso que habíamos dicho. |
Al realizar la reescritura de las coordenadas de los puntos (Figura 6), logran una perspectiva más amplia sobre la forma de variar los valores de “x”. Con ello pueden ver que para obtener el siguiente punto debían duplicar el valor anterior y sacar la raíz cuadrada (para x) así como aumentar 0.5 para los valores de “y”. Sin embargo, dudan sobre qué colocar cuando y = 0 y a su abscisa la asocian con “raíz de 1”, que corresponde al punto “B” de la construcción geométrica, punto sobre el que se les pregunta si pertenece o no a la curva (tarea 1.4).
Los estudiantes logran coordinar las operaciones de duplicar y extraer raíz cuadrada en las abscisas y sumar 0.5 en las ordenadas, que les permite generar las progresiones para “x” y “y”. Consideramos que comienzan a incursionar en los elementos de AM3, podemos decir que sus comportamientos expresados sugieren una habilidad de razonamiento covariacional (Nivel 3) de coordinación de operaciones aritméticas que generan las progresiones. Mantienen esta estrategia de duplicar en las abscisas hasta incorporar la aplicación de la raíz cuadrada para lograr atrapar todas las abscisas construidas geométricamente. Se percibe, en la discusión de los estudiantes, que pierden de vista la base 2 de la progresión geométrica analizada, al no reescribir la raíz cuadrada como exponente.
Finalmente, el análisis anterior los lleva a expresar las variaciones encontradas mediante dos expresiones algebraicas, que articulan mediante la notación de un par ordenado (Figura 7). Consideramos que la covariación estuvo latente durante todo su trabajo (línea 097 del extracto 2) y logran determinar una sola expresión para denotar la forma en que varían los puntos, pero de manera discreta, es decir, dejando las progresiones en términos de “n”, tomándolo como el representante de los números enteros que permiten determinar puntos de la curva estudiada.
Comienzan a percibir que también existen puntos a la izquierda de P1
(Figura 7) elemento de reversibilidad
en su razonamiento (AM4, nivel 4 es decir, coordinación de las operaciones que
completan las progresiones numéricas, extender de números naturales a enteros,
racional y finalmente reales) de forma discreta, ya que extienden su “n” natural
hacia los enteros, dando un ejemplo
La primera sesión finaliza invitando a los estudiantes a compartir sus conclusiones. En primer lugar, participa el Equipo 2 (no reportado en este artículo) el cual se dedica la mayor parte del tiempo a construir geométricamente nueve puntos de la curva. En su exploración, al igual que el Equipo 1, percibe dos progresiones geométricas distintas, una de números naturales y otra de números decimales que construyen multiplicando por 2 (abscisas); cada una de las cuales relacionan con una progresión aritmética que construyen sumando 1 (ordenadas). Comentan que para determinar los puntos de números enteros se puede utilizar el par (2 n , n) pero que aún no lograban encontrar la fórmula para la progresión que involucra decimales.
El Equipo 1, al coincidir con la exploración que exponen sus compañeros se
limitan a presentar su tabla numérica (Figura
5) y su conclusión (Figura 6),
respecto a que los puntos pueden ser construidos con un único par
La instrucción para la segunda sesión, fue revisar y analizar lo que se había trabajado en la primera sesión para ver si lograban percibir otros aspectos. Los estudiantes en su inquietud por descubrir la curva trabajada realizan una búsqueda de información sobre funciones exponenciales y logarítmicas, eso lo demuestran ya que al iniciar esta sesión tanto E1 y E2 afirman que la función estudiada es f (x) = log 2 x. A partir de ahí enfocan el trabajo de la segunda sesión a comprobar su afirmación utilizando las expresiones logradas en la primera sesión. Al final explican a sus compañeros que generaron un sistema de dos ecuaciones igualando las variables a su conjetura sobre la forma de determinar cualquier punto, es decir, escriben en el pintarrón:
Despejando n y utilizando función inversa logran la fórmula que necesitaban para que GeoGebra uniera los puntos con una gráfica. Se observa que no reflexionan sobre el pasaje de “números enteros” a “números reales” al generar este sistema de ecuaciones, sino que con naturalidad aceptan la continuidad de la función.
5. DISCUSIÓN
En este artículo presentamos los resultados de un experimento de enseñanza que tuvo por objetivo propiciar el desarrollo del razonamiento covariacional logarítmico-exponencial en futuros profesores de matemáticas. El experimento de enseñanza se basó en la construcción geométrica de puntos de la función logarítmica que se desea estudiar con los participantes, retomando argumentos primigenios del Cálculo (siglo XVII), que fueran rescatados de los trabajos de Ferrari (2008) y Confrey y Dennys (1997).
Encontramos que la construcción geométrica de puntos, utilizando GeoGebra, propicia un acercamiento a reconocer la covariación logarítmica-exponencial discreta trabajándose tácitamente con la continuidad de la curva al solicitar “el ajuste” de los mismos, tareas que hay que seguir afinando e investigando. En este sentido, coincidimos con Thompson y Carlson (2017) sobre que propiciar el razonamiento covariacional es crucial en el desarrollo matemático de estudiantes, en particular, al construir expresiones algebraicas, fórmulas, tablas numéricas o gráficos que les permitan describir variaciones simultáneas generando nuevos significados.
Al inicio del experimento los participantes construyeron puntos de la curva e intentaron identificar el tipo de variación que observan en las variables. Percibimos allí indicios de AM1 y de AM2 (los primeros dos niveles de coordinación y dirección), pero retenido por el entremezcle de coordenadas con pares de números enteros y aquellas coordenadas con pares de números reales. Lo primero que perciben es multiplicar por 2 y sumar 1, “saltando” así los puntos cuyas coordenadas involucran decimales. Demoran en descubrir que el patrón general de crecimiento de las abscisas es √2 y, el de las ordenadas es 0.5. Problema que reporta Gruver (2017) sobre la dificultad percibida en su investigación sobre diferenciar las relaciones lineales de las exponenciales y el cómo crecen, misma que aborda desde una recta numérica con subdivisión exponencial de segmentos generada desde los datos proporcionados a los estudiantes. Sin embargo, su atención está hacia las propiedades aritméticas de los logaritmos, no tanto hacia el reconocimiento de la covariación presente.
Ellis et al. (2016, p. 176) , por su parte, mencionan que sus hallazgos sugieren que razonar con cantidades covariando es un aspecto crítico para construir una comprensión particular del crecimiento exponencial. Idea que compartimos, desde nuestra perspectiva, pues se trata de abstraer la covariación logarítmica-exponencial desde un estudio de cantidades variando, una (ordenadas) desde la suma y otra (abscisas) desde la multiplicación. Coincidimos también con Kuper y Carlson (2017) quienes reportan que en su exploración reconocen que es crucial que los estudiantes determinen los factores de crecimiento parcial y general para reflexionar sobre la covariación logarítmica. Conclusiones que reforzamos con nuestros datos, iniciados desde una construcción geométrica.
5.1. Síntesis de resultados
En este apartado sintetizamos la producción de E1 y E2 durante la primera sesión del experimento de enseñanza, presentado en este artículo, mediante la Tabla 3 organizándola según las acciones mentales y los niveles de razonamiento covariacional logarítmico-exponencial que consideramos haber percibido en estos estudiantes según la adecuación teórica de Ferrari-Escolá, et al. (2016).
Tabla 3 Acciones Mentales de los estudiantes
| Acciones Mentales | Nivel 1 y 2 | Nivel 3 | Nivel 4 y 5 | ||
|---|---|---|---|---|---|
| AM1. Los estudiantes identifican que existe cambio constante en la diferencia de ordenadas consecutivas y aplican la misma estrategia en las abscisas: “Aquí son 51 o 52, acá no? Éste de acá son 83” (Extracto 1) sin éxito de encontrar una constante de crecimiento. Los estudiantes cambian la estrategia de “diferenciar” números consecutivos a “multiplicar”. Es decir, desde P2 (2,1) y P4 (4,2) predicen P6 (8,3) y P8 (16,4): “Porque va aumentando, el punto que tenemos es 2, luego el doble sería 4, luego el doble es 8, el doble de 8, 16” (extracto 2). | Estos niveles se entremezclan, ya que la primera tarea de esbozar la “forma” de la curva desde los puntos construidos, genera discusión entre crecimiento “cuadrático” o “logarítmico”. Distinguir entre ambos recae en reconocer las progresiones presentes (geométrica en las abscisas y aritmética en las ordenadas) | Los estudiantes se despegan de la única estrategia que utilizan al analizar la forma de crecimiento de las ordenadas de los puntos construidos (diferencia) agregando la de multiplicar. Logran entonces la dupla de factores de crecimiento: 0.5 para ordenadas y en las abscisas, unificando el cómo y cuánto crece la curva, es decir, cuál es el siguiente punto. | Los estudiantes logran una fórmula única para generar nuevos puntos. Si bien no logran una expresión general que “ajuste” los puntos en esta primera sesión, evidencian avances hacia estos niveles de razonamiento | ||
| AM2. Desde el inicio reconocen que ambas variables crecen con diferentes formas de hacerlo, sin aún lograr determinar un único factor de cada progresión que provoque su crecimiento, lo logran parcialmente en el conjunto de los números naturales. | |||||
| AM3. Logran la dupla de factores de crecimiento: 0.5 para ordenadas y √2 en las abscisas, unificando el cómo y cuánto crece la curva. “Si reemplazamos esto por lo que dijimos hace rato, éste es la raíz de 2, esta raíz de 4, esta raíz de 8, raíz de 16, raíz de 32, raíz de 64 y el punto que está aquí es la raíz de 1 es el que tenemos pues a ver cómo concebimos eso que habíamos dicho” (extracto 3). | |||||
|
AM4. Se abre la discusión desde las
coordenadas con números naturales hacia coordenadas con
números reales de manera discreta, evidenciando tímidamente
reversibilidad en su razonamiento, al menos presentan un
ejemplo: |
|||||
|
AM5. Generan una expresión general para
describir la curva de manera discreta, es decir, dan una
“fórmula” general para construir cualquier punto |
|||||
Observamos entonces que, durante gran parte del experimento de enseñanza E1 y E2 se enfocan en determinar cómo obtener el siguiente punto de la curva mediante un análisis cuantitativo, apoyándose en GeoGebra para comprobar su conjetura, no para construirlos. Con este estudio logran coordinar las operaciones aritméticas (al menos para los números naturales) de multiplicar por 2 y sumar 1, que les permite generar las progresiones para “x” y “y”. Sin embargo, van dejando huecos, aquellos que implicaban números reales, aso-mándose así a AM3 de manera sesgada sin poder aún relacionarlas con el comportamiento logarítmico. Ello fortalece lo que Ferrari-Escolá, et al. (2016) se refieren al mencionar que si bien, concebir la simultaneidad de dos variaciones diferentes cuyos cambios se afectan entre sí conduce al razonamiento covariacional, la complejidad cognitiva radica en percibir la coexistencia y la codependencia de las progresiones.
5.2. Sobre la continuidad tácita
Respecto al tipo de variación, Castillo-Garsow (2010, 2012) distingue dos concepciones de variación continua que denomina “chunky” y “smooth”, elementos que son considerados también por Thompson y Carlson (2017) como los niveles más avanzados del razonamiento covariacional (Covariación continua a trozos - Covariación continua suave). Consideran entonces, que la variación continua a trozos implica pensar que los valores varían discretamente, es decir, que existen huecos entre dos puntos consecutivos aunque el fenómeno estudiado sea constante y donde el estudiante tiene una imagen tácita de un continuo entre valores sucesivos. En tanto que, consideran que la covariación continua suave implica concebir los cambios (aumentos o disminuciones) en el valor de una cantidad o variable tal como ocurre, simultáneamente, con los cambios en el valor de la otra variable, y se abstrae que ambas variables varían de manera continua y suave. Ellis et al, (2016), coincide con esta idea, ya que consideran que el razonamiento covariacional temprano en estudiantes que logran describir numéricamente el crecimiento de un cactus, precede a su capacidad de desarrollar reglas de correspondencia de la forma y = f (x).
En nuestro diseño, provocamos en los participantes la concepción de variación simultánea discreta durante las tareas, debido a que nuestro experimento de enseñanza inicia desde la construcción geométrica de puntos invitándolos a reflexionar sobre covariación continua al solicitar ajustar los puntos, ya que la tarea general es describir la curva que “une” los puntos. Observamos que E2 menciona que los puntos se van “ensanchando” refiriéndose a las abscisas, implicando la desaceleración del crecimiento de la curva, es decir, evoca a la función logarítmica que es discutida por su compañero que insiste en que se trata de una parábola. Idea que se diluye al insistir con hacer diferencias entre cantidades consecutivas, estrategia apropiada para funciones polinomiales pero desafortunada para funciones trascendentes.
Un software como GeoGebra, exige una expresión análitica para trazar una función determinada, desafío que propone como cierre de la discusión las tareas diseñadas en el experimento de enseñanza. Su pantalla “vista gráfica”, permite visualizar la forma de crecimiento de los puntos que geométricamente se construyen; así como, la pantalla “vista algebraica” explicita las coordenadas de cada punto determinado. Un razonamiento covariacional cuantitativo de los estudiantes se percibe al construir una columna de pares ordenados de la cual organizan sus ideas sobre los patrones de crecimiento de cada ordenada (multiplicación para las abscisas y sumar para las ordenadas). Coincidimos con Ellis et al, (2016) respecto a que los estudiantes abstraen el crecimiento implicado covariacional-mente considerando un nuevo valor como producto de un valor anterior y un factor de crecimiento, forma de pensar que corresponde intrínsecamente a una covariación continua a trozos. Si bien logran, luego de investigar en internet, la fórmula: f(x) = log 2 x y explicar su hallazgo desde una manipulación algebraica de un sistema de ecuaciones (segunda sesión del experimento de enseñanza); no podemos asegurar que hayan evolucionado a un razonamiento covariacional continuo suave. Visualmente observan cómo la curva pasa por todos los puntos que han construido, es decir, logran ajustar los puntos pero no se cuestionan sobre cómo establecer la continuidad de la función cuando pasan de utilizar “n” representan-te de los enteros que también involucra a algunos números irracionales a “x” y “y” como números reales. Es decir, de un dominio discreto a ℜ+ y de un codominio de números racionales a uno de números reales.
Para Thompson y Carlson (2017), la instrucción matemática escolar generalmente enfatiza la perspectiva de correspondencia a expensas del razonamiento covariacional, lo que puede fomentar una imagen de función restringida, ya que no se anima a los estudiantes a pensar en el cambio entre variables. Incluso, para nosotros, es necesario desarrollar en los estudiantes la habilidad de reconocer funciones desde un razonamiento covariacional cuantitativo que involucra el reconocimiento de patrones de crecimiento que abonen a la determinación de una expresión algebraica y construir nuevos significados de la continuidad de funciones.
6. CONCLUSIONES Y FUTURAS INVESTIGACIONES
En el experimento de enseñanza desarrollado, en los dos futuros profesores
estudiados, se evidencia fragilidad en sus estrategias matemáticas ya que, en
laprimera sesión, si bien logran una expresión general
Dado el carácter cognitivo de nuestra investigación consideramos que el hecho que nuestra evidencia empírica surja de la cognición de dos de los participantes no representa una debilidad. De hecho, este tipo de exploraciones con unos pocos participantes es común en el campo de investigación acerca del razonamiento covariacional (e.g. Moore, 2014; Paoletti y Moore, 2017). En este sentido, nuestros resultados invitan a continuar afinando el diseño de aprendi-zaje desde construcciones geométricas, ya perdidas en el ámbito escolar así como en las investigaciones, mismas que hemos evidenciado provocan exploraciones generadoras de razonamiento covariacional en estudiantes, dándoles la posibilidad de probar sus conjeturas numéricas al predecir nuevos puntos de la curva estudiada.
Consideramos importante seguir explorando el pasaje de lo discreto a lo continuo desde construcciones geométricas, argumento que sustenta las prime-ras ideas de Cálculo en siglos pasados a manos de personalidades como Descartes, Newton, Huyens, Agnesis o Euler. Un ambiente de geometría dinámica nos permite replantearnos el significado de funciones particulares como las funciones trascendentes y su continuidad en el razonamiento de los estudiantes al contar con herramientas como “vista algebraica-gráfica-hoja de cálculo-cálculo simbólico” cuya articulación podría fortalecer el desarrollo del razonamiento covariacional logarítmico exponencial de futuros profesores.











 text new page (beta)
text new page (beta)