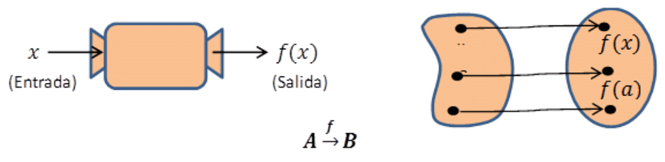INTRODUCCIÓN
Una aspiración en las carreras de ingeniería de la Universidad de Camagüey Ignacio Agramonte Loynaz es mejorar los indicadores globales de calidad del Ministerio de Educación Superior, reflejados en los objetivos de trabajo del curso 2016-2017 (colectivo de autores, 2014). Un reciente análisis cuantitativo-cualitativo del proceso de enseñanza-aprendizaje de las matemáticas en nuestro departamento, demuestra que la calidad de los aprendizajes de los estudiantes no permite alcanzar tal propósito. En los informes de la asignatura Matemática I, donde se imparte el contenido básico de cálculo diferencial e integral de funciones reales de una variable real, ha quedado confirmado que: el trabajo con las funciones y su aprendizaje aún no responde a una sólida comprensión de su estructura y apropiación en todos los temas de matemáticas impartidos en las carreras de ingenierías, lo cual ha provocado el pobre desenvolvimiento en el trabajo con los conocimientos de función, tanto en los docentes como en los alumnos.
En la actualidad, el problema del aprendizaje de las funciones reales en la educación superior constituye una dificultad aún no resuelta. El estudio llevado a cabo por Amaya, Pino-Fan & Medina (2016) revela la persistencia en la falta de comprensión del concepto función y en su identificación; así se corrobora en otros estudios hechos por Godino, Bencomo, Font & Wilhelmi (2006), donde se afirma que el conflicto epistémico más marcado en relación con el concepto de función, es el distanciamiento entre el reconocimiento del concepto a nivel escolar y su uso consciente en el ámbito social. Los significados asociados al trabajo con los conceptos matemáticos que se pretenden, impactan en la formación de ingenieros.
Se dice, que en los procesos de instrucción y aprendizaje del conocimiento matemático el tratamiento de los contenidos se hace de forma fragmentada y descontextualizada, sin que se revelen a los alumnos vínculos y relaciones entre ellos, así como de estos con las asignaturas de la profesión (Montes de Oca, Rubio & Núñez, 2016: 2).
De manera particular, consideramos la fragmentación y la descontextualización en el tema de funciones reales de una variable real -vistas desde una arista intra-matemática- como el insuficiente apoyo que existe entre los diferentes registros semióticos del concepto de función, para el desarrollo de las diferentes actividades matemáticas que en la formación de ingenieros deben ser resueltas, lo que provoca la prevalencia del uso algebraico sobre los restantes, al igual que la aplicación de este concepto en los disímiles contextos en los cuales se presenta. Por tal motivo, nos inclinamos por estudiar los significados y sus vínculos, que son pretendidos en la enseñanza del concepto de función real de una variable real en las carreras de ingeniería en la Universidad de Camagüey.
El proceso de formación en la educación superior cubana tiene el objetivo de preparar integralmente al alumno en una determinada carrera universitaria. Supone brindar los conocimientos y las habilidades necesarias para el desempeño profesional, y también utilizarlos en la solución de los problemas que se le presenten como parte de su actividad laboral (Horruitiner, 2009).
Existen estudios en cuanto a prácticas matemáticas en la enseñanza y el aprendizaje de las funciones reales de una variable real, entre los que se encuentran Hitt (2003), Godino, Bencomo, Font & Wilhelmi (2006), Duval (2006), Mendible & Ortiz (2007), Godino, Batanero & Font (2007) y Amaya et al. (2016), entre otros. A manera de síntesis, estos autores han señalado que en profesores y alumnos con frecuencia se utiliza la manipulación de representaciones algebraicas, y esto produce limitaciones en su comprensión. Sin embargo, las actividades que involucran transformaciones ventajosas de tipo conversión y tipo tratamiento (Duval, 2006) son minimizadas por los profesores al estudiar las funciones (Amaya et al. 2016). Esto se verifica cuando existen otras tendencias que dan prioridad al estudio del concepto función, sobre la base del análisis gráfico (Berciano, Ortega del Rincón & Puerta, 2015).
Varios autores (Vinner, 1991; Dubinsky & Harel, 1992; Stewart, 2006 y Berciano et al., 2015) recomiendan y asumen la representación de las relaciones funcionales de forma verbal, algebraica (analítica y por secciones), tabular y gráfica, en tareas fundamentalmente de traducción. Sin embargo, según Berciano et al. (2015), la representación gráfica facilita ver las características globales de la función, y la ecuación permite determinar con precisión valores de ambas variables. Si bien son ciertas estas conclusiones, a la vez provocan que prevalezca el uso de un registro sobre otros, por lo que los vínculos operacionales y procedimentales en la realización de conversiones y tratamientos, dificultan la comprensión y apropiación del concepto de función.
El aprendizaje del concepto de función no se desliga de su componente semiótico, como se ha visto anteriormente, componente que se refiere a un significado numérico, algebraico, geométrico y verbal, pero que también interviene en las prácticas de enseñanza influenciadas por documentos rectores y directivos; y estas, a su vez, configuran un significado institucional que es llevado de forma planificada al discurso en nuestras aulas. Debido a la manera en que este significado institucional o pretendido del concepto de función es implementado, se hace necesario caracterizarlo, pues tendrá lugar inmediatamente en las prácticas operatorias de nuestros estudiantes que se forman como ingenieros.
Estos motivos generan el problema: ¿cuáles son los significados concretos del concepto de función real de una variable real que deben enseñarse a los ingenieros? y tiene la intención de contribuir al perfeccionamiento de la enseñanza de las matemáticas en el nivel superior, para la formación integral de la cantera de futuros científicos en diferentes ramas de la ciencia, del Proyecto Nacional 2016-2020 “Perfeccionamiento de la enseñanza de la matemática”.
El objetivo de nuestra investigación es identificar los significados institucionales (prácticas institucionales) pretendidos con criterios de mejora para la enseñanza del concepto de función que podemos encontrar en los planes y programas de estudio de matemáticas, así como en los libros de texto básicos de las carreras de ingeniería. Estas prácticas serán caracterizadas y analizadas a través del complemento didáctico-matemático del Enfoque Onto-Semiótico (EOS) del Conocimiento y la Instrucción Matemática (Godino & Batanero, 1994; Godino et al. 2007), la idoneidad didáctica (Godino, Font, Contreras & Wilhelmi, 2006) del proceso de enseñanza del concepto función real de una variable real, de manera que solo se tome la dimensión epistémica y los criterios dados por Pino-Fan, Castro, Godino & Font (2013), que se da en este proceso instructivo en la actualidad.
NOCIONES TEÓRICAS
LA ENSEÑANZA DE LAS MATEMÁTICAS EN LA FORMACIÓN DE INGENIEROS
Se consideran objeto de las matemáticas todas las formas y relaciones del mundo real que poseen objetivamente tal grado de independencia respecto al contenido, que pueden ser totalmente abstraídas de este último. Además, no solo las formas abstraídas de la realidad son objeto de estudio de las matemáticas, sino también aquellas lógicamente posibles, determinadas sobre la base, formas y relaciones ya conocidas. La enseñanza de las matemáticas en la formación de un ingeniero es aquella donde todo ingeniero considera representaciones técnicas y científicas en términos matemáticos, con los cuales refleja los rasgos cuantitativos de los fenómenos que estudia. De tal modo, el objetivo de esta disciplina es lograr que el ingeniero domine el aparato matemático que lo haga capaz de modelar y analizar los procesos técnicos, económicos, productivos y científicos, de manera que utilice en ello tanto métodos analíticos como aproximados, y use eficientemente las técnicas de cómputo.
El diseño de diferentes planes y programas de estudio ha dedicado atención al concepto de función, pues ha sido caracterizado en la formación del ingeniero como conocimiento previo, invariante del conocimiento, conocimiento básico y línea directriz para el estudio de diferentes temas de matemáticas. Lo cierto es que su contenido es una prioridad indispensable para cualquier proceso de enseñanza de las matemáticas. En la asignatura Matemática I impartida como tronco común en todas las ingenierías de la Universidad de Camagüey Ignacio Agramonte Loynaz, se dispone aproximadamente de 6 horas de clases para desarrollar el tema de funciones reales de una variable real.
PRINCIPALES SIGNIFICADOS DEL CONCEPTO DE FUNCIÓN REAL DE UNA VARIABLE REAL EN LAS MATEMÁTICAS Y EN SU ENSEÑANZA
El concepto de función está presente en todas las matemáticas. No solamente es central en las áreas propias de las matemáticas (llamadas teóricas o puras), sino que es la herramienta por excelencia en las áreas que buscan modelar o describir las actividades cotidianas y los fenómenos que se perciben (Ugalde, 2014). A partir de la forma más primitiva de contar y del intento de comprender situaciones cotidianas del hombre, este autor define algunos significados, los cuales podemos interpretar como significados primitivos del concepto de función, que fueron atribuidos inicialmente durante su evolución histórica. Entre ellos está la relación entre las cantidades de los conjuntos, la tabulación primitiva de algunos fenómenos o cuentas, la trigonometría, leyes de la física, crecimiento de poblaciones, interés simple o compuesto.
Las representaciones del concepto de función, según Azcárate & Deulofeu (1990), son mediante una descripción verbal, diagramas, tablas de valores, gráficas y relación algebraica. Cada una de estas representaciones constituye significados, donde necesariamente el aprendizaje de este concepto requiere de la interacción entre ellos, y no solo por la lógica propia del conocimiento, sino también por la lógica del aprendizaje de los estudiantes.
Una visión amplia sobre el significado de función se tiene a partir de sus representaciones, cuando se define como correspondencia entre conjuntos, relación entre magnitudes variables, representación gráfica, expresión analítica, correspondencia arbitraria y la función a partir de la teoría de conjuntos (Amaya et al. 2016). El concepto de función como se entiende hoy se consolidó en 1837, con el matemático Gustav Dirichlet, aunque Gottfried Leibniz en 1673 ya había expresado algunas ideas al respecto en sus trabajos (Parra, 2015). El estudio histórico-epistemológico sobre este concepto realizado por Parra (2015) señala que las ideas de Dirichlet responden a interpretar la función como una correspondencia arbitraria, lo que nos permite, para nuestro análisis, incluir aquellas funciones definidas por secciones u otras que también son objetos de estudio en las carreras de ingeniería. Stewart (2006) precisa que una función es una regla, lo cual también brinda al concepto un carácter general y arbitrario. Por otra parte, algunos autores atribuyen a Galileo la introducción de manera formal del concepto de función en las matemáticas.
En la antigüedad (Babilonia y Egipto) las matemáticas -desde el punto de vista del concepto de función- se limitaban a la elaboración de tablas de mediciones de los fenómenos observados. Luego aparecen las matemáticas griegas, en particular los trabajos de Arquímedes, con las primeras leyes de la cinemática. En la edad media, en muchas áreas del pensamiento humano se vislumbraron las primeras representaciones gráficas sencillas asociadas a los movimientos y cambios observados en los fenómenos naturales. El mayor auge del concepto de función se dio durante los siglos XVI, XVII y XVIII, con el desarrollo de los números reales y el análisis matemático.
FUNDAMENTOS EPISTÉMICOS DEL ENFOQUE ONTO-SEMIÓTICO PARA LA CONSTRUCCIÓN DEL CONOCIMIENTO MATEMÁTICO, EN EL CASO PARTICULAR DEL CONCEPTO DE FUNCIÓN REAL DE UNA VARIABLE REAL
En el proceso de enseñanza de las matemáticas, donde también tiene lugar la apropiación de sus contenidos por los estudiantes, los significados de tales contenidos son transmitidos a partir de enfoques, concepciones y estrategias asumidas desde la didáctica. La apropiación de los significados se consolida en la medida en que son usadas las definiciones, propiedades y los procedimientos que los involucran. Estos son mediados por registros semióticos que permiten evaluar las operaciones que realizadas con los significados.
Para describir la operatividad del concepto de función a partir de sus significados en el proceso de enseñanza y aprendizaje de las matemáticas, y su implicación en la formación de ingenieros, es necesario recurrir a enfoques que brinden una herramienta metodológica que contribuya a caracterizar y describir, como se pretende en las diferentes directrices curriculares que aparecen en planes, programas y libros de texto de la asignatura, al igual que la articulación entre tales conocimientos significativos. Por esto en la presente investigación adoptamos el modelo teórico conocido como Enfoque Onto-Semiótico (EOS) del Conocimiento y la Instrucción Matemática, desarrollado en diversos trabajos por Godino y colaboradores (Godino & Batanero, 1994; Godino et al., 2007) para lograr el objetivo propuesto.
Dicho marco teórico incluye un modelo epistemológico y cognitivo de las matemáticas, sobre bases antropológicas y socioculturales; un modelo cognitivo sobre bases semióticas de índole pragmática, y un modelo instruccional coherente con los anteriores. Para nuestro análisis es importante la elección de este enfoque, pues consideramos que no solo posibilita describir aspectos del aprendizaje de los sujetos que aprenden, sino que permite explicar cuáles son los factores que inciden en las dificultades y establecer criterios para orientar la construcción y perfeccionamiento del conocimiento matemático en la enseñanza y el aprendizaje. Los elementos fundamentales de este enfoque que resultan novedosos para la didáctica de las matemáticas, y que sustentan nuestro propósito, son los componentes epistémicos y sus configuraciones. De este enfoque tomaremos en cuenta la noción de idoneidad epistémica (Pino-Fan et al., 2013) que se refiere al grado de representatividad de los significados institucionales pretendidos (o implementados) respecto a un significado de referencia, que en nuestro caso es el significado matemático o global del concepto de función.
Utilizaremos los criterios para la idoneidad epistémica dados por Pino-Fan et al., (2013), contextualizados en la enseñanza y el aprendizaje de las matemáticas en la Universidad de Camagüey, debido al trabajo sistemático que se hace con la funciones en los temas de límite y continuidad, derivada y cálculo integral con funciones de una variable real, sin descuidar que la tendencia al perfeccionamiento de los planes de estudio es integrar el sistema de conocimientos y reducir el número de horas para tratar los temas del cálculo diferencial e integral. Estos fundamentos epistémicos nos permiten analizar y describir sistemáticamente los objetos matemáticos primarios y su relación con las actividades de aprendizaje a partir de su descriptor, como se propone:
Situaciones/problemas: propuesta de situaciones que generan conversiones y tratamientos de variadas formas de representación del concepto de función, uso de medios tecnológicos y aplicaciones del concepto.
Conceptos/definiciones: características esenciales y no esenciales, propiedades comunes y no comunes que se analizan y expresan en el lenguaje matemático (verbal, gráfico, simbólico). Clasificaciones y relaciones conceptuales que se determinan.
Elementos de representación semiótica: implementación de procesos y tipos de representaciones de la actividad matemática que se proponen.
Proposiciones/propiedades: adecuación de las explicaciones, deducciones, enunciados, comprobaciones y demostraciones al nivel que se trata.
Procedimientos y argumentos: empleo de reglas, principios, pasos y estrategias que se utilizan para el análisis de significados.
En nuestra concepción, estos objetos matemáticos son utilizados en instituciones y destinados a la resolución de problemas y preparación del conocimiento que antecede al resto de las temáticas del cálculo diferencial e integral. La sólida apropiación de los significados garantiza el desarrollo de la práctica matemática. Las prácticas institucionales que están asociadas al concepto de función se refieren a la implementación planificada y concatenada del contenido matemático, en la documentación normativa (planes de estudio, programas de asignatura y libros de texto, entre otros elementos) que predominan en los docentes de matemática para el desarrollo del tema. Las prácticas personales se observan en el desempeño operacional de los estudiantes durante la interacción con el contenido matemático. Estos objetos que intervienen en las prácticas matemáticas institucionales y personales sobre el concepto de función real de una variable real, son propuestos en los planes de estudio, programas y libros de texto básicos.
La metodología aplicada en esta investigación, dirigida a identificar los significados institucionales o prácticas institucionales que se pretenden sobre el concepto de función real de una variable real, tiene en cuenta tres momentos principales: 1) La determinación de un significado global de referencia para el concepto de función; 2) La determinación del significado pretendido para el concepto de función en los planes y programas de estudios, y en los libros de texto considerados básicos; y 3) La aplicación de los fundamentos o criterios de idoneidad epistémica precisados con anterioridad, para valorar dichos significados y brindar criterios sobre su mejora.
La metodología propuesta se apoya y adapta a la dada por los autores Pino-Fan et al. (2013), en cuanto a su caracterización del significado epistémico de la derivada. Está elaborada mediante una revisión de tipo histórico-documental, en artículos científicos referenciados que abordan este concepto, además del empleo de criterios y configuraciones epistémicos que contribuyen a obtener los significados que se quieren.
ASPECTOS METODOLÓGICOS
CARACTERIZACIÓN DE LOS PROCESOS DE ESTUDIO CON EL CONCEPTO DE FUNCIÓN
En el análisis y estudio de los procesos de enseñanza y aprendizaje de las matemáticas, observamos que últimamente gran parte de las investigaciones en didáctica de las matemáticas se desarrollan alrededor del uso de nociones que permiten materializar los conceptos matemáticos mediante diferentes conjuntos de símbolos y gráficos. Varios autores (Vrancken, Engler & Müller, 2012; Nardín, Álvarez, Blanco, Bueno & Mora, 2012; Herrera, Cuesta, Escalante & Juana, 2016; Amaya et al., 2016) hacen referencia a las representaciones semióticas y a las representaciones mentales, y sostienen que el desarrollo de las representaciones mentales se lleva a cabo como una interiorización de las representaciones externas.
Las representaciones matemáticas se entienden como herramientas (signos o gráficos) que hacen presentes los conceptos y procedimientos matemáticos, con las cuales los sujetos registran y comunican su conocimiento; esto es, las estructuras matemáticas adquieren significado para el sujeto mediante el trabajo con las representaciones, y de aquí surge parte de su interés didáctico. No es posible estudiar los fenómenos relativos al conocimiento, su aprendizaje y su desarrollo en el desempeño de los docentes y estudiantes, sin recurrir a la noción de representación en matemáticas.
Entre las formas de representación más generales de los contenidos matemáticos estudiados en el nivel superior en las carreras de ingeniería, se distinguen dos familias de sistemas: las representaciones simbólicas y las gráficas. Las representaciones simbólicas son de carácter alfanumérico (es un término más general que incluye letras y números, así como la combinación de estos). Representaciones numéricas, verbales y analíticas son ejemplos de este tipo de sistema de representación. Se pueden simular mediante programas informáticos, y la sintaxis es descrita mediante reglas de procedimientos.
Las representaciones gráficas incluyen las de tipo figurativo, de carácter analógico, y su sintaxis viene dada por reglas de composición y convenios de interpretación. Los registros semióticos incluyen ambos tipos de representaciones, al igual que en su aprendizaje se implementan e interactúan estas representaciones. El uso de los sistemas de representación es un medio de expresión que caracterizados por signos propios y forma en que se organizan, aspecto que debe ser considerado al evaluar el desempeño cognitivo de los estudiantes durante la actividad matemática que se realiza.
Un objeto matemático puede ser descrito a través de su dimensión personal e institucional, si se tiene en cuenta que de forma personal se utiliza un significante para darle un significado a dicho objeto durante la actividad matemática. Lo institucional está determinado por las actuaciones que pretende la enseñanza en la relación significante-significado (Godino & Batanero, 1994), la cual es referenciada en las directrices curriculares de la asignatura matemática I. Los tipos de representación que utilizan la relación significante-significado, mencionados por Hitt (2003) y Duval (2006), unidos a los procesos de conversión, forman un sistema de representaciones capaz de integrar los distintos contextos matemáticos. A manera de ejemplo, vemos que un gráfico (significante) de una función (significado gráfico) puede ser convertido en una ecuación algebraica (significante) de la función (significado algebraico o analítico).
Sobre la representación de un concepto, Fernández-Millán & Molina (2016) caracterizan el significante y expresan el contenido de un concepto (significado) al plantear que es un conjunto estructurado de notaciones, símbolos y gráficos, con reglas y convenios, que permite expresar aspectos y propiedades de un concepto -en forma más específica, sus elementos-, solo añadimos que los sistemas de representación también reflejan la comprensión y el modo de solución de tareas de aprendizaje, por ejemplo la resolución de problemas durante el proceso de formación de los estudiantes.
Las funciones son los objetos fundamentales con los que trata el cálculo diferencial e integral, donde sus representaciones tabular, verbal, gráfica y analítica también se pueden transformar y combinar para modelar matemáticamente fenómenos del mundo real. Las funciones siempre surgen cuando una cantidad depende de otra (Stewart, 2006), por tal motivo, su generalización se puede modelar cuando nos encontramos con conjuntos de variables ligadas entre sí (Kudriávtsev & Demidóvich, 1989). Este criterio se inclina más hacia representaciones analíticas de las funciones.
Los significados que se pretenden con el concepto de función pueden ilustrarse a partir de la configuración epistémica dada por Godino, Bencomo, Font & Wilhelmi (2006), la cual considera objetos matemáticos primarios alrededor de las representaciones semióticas del concepto de función, que pueden ser descritos y caracterizados.
Después de estas consideraciones, es posible proponer criterios que permitan analizar y caracterizar los significados del concepto función real de una variable real, que se pretenden en el proceso de enseñanza-aprendizaje en las carreras de ingeniería. A partir de dicha caracterización podemos emitir criterios de mejora sobre la idoneidad epistémica y su relación con el aprendizaje de los alumnos.
De todo lo abordado hasta el momento, consideramos que las prácticas institucionales, u objetos matemáticos primarios acerca del concepto de función real de un variable real, nos acercan hacia una concepción de apropiación de este concepto. En el marco de la teoría de las representaciones semióticas (Hitt, 2003; Duval, 2006) se definen los contextos matemáticos más importantes donde ocurren las representaciones, los procedimientos utilizados para la conversión y el tratamiento de registros semióticos, así como los principales significados del objeto matemático.
CRITERIOS PARA EL ANÁLISIS DE LA DIMENSIÓN EPISTÉMICA EN EL ESTUDIO DE LAS FUNCIONES
El significado del concepto de función, analizado desde sus orígenes hasta la actualidad permite establecer un significado de referencia. Los significados parciales, institucionales o pretendidos, subordinados a estos referentes, serán elementos de análisis en la caracterización de la idoneidad epistémica del concepto estudiado. “La idoneidad epistémica, se refiere al grado de representatividad de los significados institucionales implementados (o previstos), respecto de un significado de referencia” (Godino, Bencomo, Font & Wilhelmi, 2006: 4).
Por considerar que los criterios dados por Pino-Fan et al. (2013) en el análisis epistémico de la derivada son generales, los tomaremos en cuenta para el análisis de los significados pretendidos del concepto abordado, y realizaremos algunos ajustes en ellos, debido a la evolución de las exigencias del proceso de enseñanza y aprendizaje de las matemáticas en la actualidad.
I. Representatividad de los campos de problemas propuestos
Este criterio refleja las tareas matemáticas que requieren de los objetos y significados matemáticos que promueven el aprendizaje de los significados definidos en el entorno del concepto de función. La resolución de problemas es un objetivo de enseñanza y aprendizaje en matemáticas, pues se tiene en este proceso que:
Los problemas son usados como medio, objeto y método. Como medio, ya que se usan como el instrumento adecuado para la introducción de temas, el desarrollo de métodos y en general la formación de algunas habilidades; como objeto, pues el propósito principal en las actividades del proceso de enseñanza y aprendizaje es la resolución de problemas y como método ya que mediante dichos problemas se posibilita la introducción de métodos, procedimientos, etc. (Yordi, 2004: 17-19).
Los significados de los objetos matemáticos están relacionados con los sistemas de prácticas que aparecen principalmente en presentaciones del contenido, ejemplos y ejercicios que se proponen. Estas prácticas matemáticas, constituidas por concepciones, enfoques, orientaciones, etc., del aprendizaje del contenido matemático, se presentan esencialmente por acciones implementadas y que son planificadas para ser transmitidas en la enseñanza del concepto de función, se vinculan con los problemas representativos del campo correspondientes a los significados institucionales del concepto que se estudia.
CP1: determinación de relación entre magnitudes.
CP2: cálculo y estimación de valores funcionales.
CP3: representación de funciones en situaciones intra-matemáticas.
CP4: modelación de situaciones prácticas mediante funciones.
CP5: representación de funciones en computadoras u otros dispositivos electrónicos.
II. Procesos de representación activos en el planteamiento y solución de las tareas
Durante el proceso de análisis de la idoneidad epistémica es necesario considerar los distintos tipos de representaciones (lenguaje matemático) utilizados para referirse a los diferentes objetos matemáticos, así como los tratamientos y conversiones entre ellos.
De acuerdo con Berciano et al. (2015), existen cuatro formas fundamentales de representar una función: tabular, verbal, gráfica y analítica, aunque deben considerarse otras formas de ilustrar correspondencias unívocas entre dos conjuntos numéricos. Tal es el caso de los diagramas de Venn o de flechas, de máquinas, sagitales, entre otras que también forman parte de la actividad matemática en el desempeño profesional del ingeniero. La figura 1, muestra algunos de estos ejemplos, que son poco usados en la formación matemática del ingeniero debido a la prevalencia de lo analítico y gráfico en el trabajo con funciones, y que tienen una alta significación en el desarrollo del concepto de función en la actualidad.
Traducción o conversión de situaciones de la vida.
Conversión y tratamiento en las distintas formas de representación.
Traducciones y conversiones entre las distintas formas de representación.
Visualización de las formas de representación.
III. Representatividad de los elementos regulativos y argumentativos
Los elementos regulativos y argumentativos (definiciones, proposiciones, procedimientos y argumentos) relativos al concepto de función, son mediados a través de los elementos lingüísticos que hemos mencionado y sirven para identificar con claridad los significados más usados por los docentes y estudiantes durante el estudio de este concepto. Los elementos lingüísticos descritos e identificados sobre los conocimientos de función que se exponen en los planes y programas de estudio de matemáticas, como también en libros de textos en las carreras de ingeniería, destacan la ampliación de significados institucionales del concepto función.
IV. Conocimientos previos a la profundización del concepto de función
Este criterio se refiere a las formas previas de definir, analizar y representar el concepto de función, y su relación con su presentación en los libros de texto, al igual que en los planes y programas de estudio de matemáticas. Para comprender y valorar esta relación tomamos en cuenta los principios básicos brindados por Pino-Fan, Guzmán, Font & Duval (2017) acerca de la teoría de los registros de representación semiótica (TRRS), donde:
Existen tantas representaciones semióticas diferentes del mismo objeto, como registros semióticos usados en matemáticas.
Cada representación semiótica diferente del mismo objeto matemático no indica explícitamente las mismas propiedades del objeto que se representa. Lo que se afirma explícitamente es el contenido de la representación.
El contenido de las representaciones semióticas nunca debe confundirse con el objeto matemático que representa.
Esto permitirá encontrar y caracterizar en la comprensión y resolución de ejercicios y problemas, como forma de actividad matemática, elementos sobre los tipos de representaciones y los procedimientos para la conversión y el tratamiento entre estos.
V. Representatividad de los significados institucionales pretendidos (o implementados) respecto al significado global de referencia
El sistema de enseñanza en las carreras de ingeniería se concibe para que el estudiante pueda apropiarse de los conocimientos incluidos en el programa de las asignaturas de matemáticas, el cual deriva de los planes de estudios de cada carrera y propone el trabajo con los significados institucionales que tienen los libros de texto básicos de cada carrera. Todo esto forma parte del currículo.
Luego, los contenidos matemáticos que aparecen en los planes de estudio, programas de las asignaturas y los significados que se les da en los textos básicos serán, en nuestro caso, los significados institucionales pretendidos de referencia.
Para que la instrucción sea epistémicamente idónea, este conjunto de objetos y significados institucionales de referencia debe representar el significado global del concepto de función real de una variable real. El énfasis en determinados significados y objetos matemáticos, y el desconocimiento de otros, puede resultar en un cubrimiento epistémico parcializado que puede afectar la idoneidad del proceso de instrucción (Pino-Fan et al., 2013).
Los cinco criterios de idoneidad epistémica mencionados son descritos en el siguiente apartado en el que, además de mostrar las configuraciones de objetos y sistemas de prácticas de los planes de estudio, programas y libros de texto, elaboramos el análisis de la idoneidad epistémica a partir de los principales significados globales de los significados institucionales de referencia sobre el concepto de función.
SIGNIFICADO EPISTÉMICO (PRETENDIDO) DEL CONCEPTO FUNCIÓN EN LOS PLANES Y PROGRAMAS DE ESTUDIO DE MATEMÁTICA
De los significados histórico-didácticos sobre la construcción del concepto función y su implementación en el proceso de formación de los ingenieros, que aparecen en los planes y programas de estudio para el análisis de las configuraciones epistémicas, se tienen en cuenta los aspectos siguientes:
Los significados de las funciones que actualmente se pretenden en los planes y programas de estudio de las carreras de ingeniería.
Exigencias sobre la implementación de los significados (objetivos, propósitos, fines, etc.).
La relación entre los significados histórico-didácticos y los significados pretendidos.
En el plan de estudio y los programas de matemáticas en la formación de ingenieros se pueden constatar los significados pretendidos. La Tabla 1 resume los componentes epistémicos-didácticos (conjugación de un componente epistémico con uno del proceso de enseñanza y aprendizaje) y su contenido (conocimiento, acciones, habilidades y problemas, entre otros), que conforman un significado pretendido para la enseñanza y el aprendizaje del concepto de función en las carreras de ingeniería.
Tabla 1 Resumen de los significados pretendidos por los componentes epistémicos-didácticos en la enseñanza del concepto de función en las carreras de ingeniería.
En cuanto al trabajo con funciones, el plan de estudios que contiene las orientaciones establecidas por el Ministerio de Educación Superior respecto al diseño curricular de cada carrera, donde aparecen la disciplina Matemática y sus asignaturas por semestre y años, se dirige a satisfacer las demandas actuales y futuras a nivel nacional de los Organismos de la Administración Central del Estado (OACE) y los programas de estudio de las asignaturas, y propone: 1) “analizar desde variadas formas de representación, disímiles relaciones que se establecen entre magnitudes, lo que permitirá dar soluciones a tareas y problemas de la vida práctica y profesional del estudiante al facilitarle la formulación de modelos matemáticos de problemas financieros, químicos, ecológicos, físicos y geométricos”; 2) “el estudio de funciones reales de mayor complejidad”. Para esto, son determinadas las propiedades generales y particulares de las funciones, al igual que las clasificaciones de las funciones reales, lo cual permite solucionar distintas tareas con relación al tema de funciones. 3) “el uso de los asistentes matemáticos para el análisis y la representación de funciones reales de cualquier clasificación”. Aquí se determinan los asistentes más usados en la formación de ingenieros, como es el Derive, Matlab y Maple, entre otros, lo cual permite la exploración, la interacción con nuevos tipos de funciones, para así poder resolver tareas de gran envergadura en el proceso de instrucción.
Respecto a los conceptos/definiciones, el plan de estudios y los programas resaltan algunos, tales como los de función (polinómica, racional, algebraica, trascendente, por parte o secciones).
Entre las proposiciones se consideran: las propiedades generales y particulares de las funciones; las reglas o leyes (las formas posibles de representar una función); las propiedades o teoremas fundamentales para el análisis y la interpretación de funciones o modelos funcionales vinculados con situaciones de la vida práctica. Los procedimientos presentados están indicados para el desarrollo de las habilidades de cálculo con valores funcionales, análisis de propiedades generales y particulares, interpretación de modelos funcionales, representación de funciones en forma analítica y gráfica (fundamentalmente de aquellas elementales y no elementales que sean posibles) resolución de problemas de la vida práctica, al igual que así como para el uso de asistentes matemáticos en el cálculo, la representación y validación de propiedades.
Entre los argumentos principales que se pretenden para comenzar el estudio de las funciones está la determinación de relaciones funcionales entre magnitudes, la observancia de la variación de una con respecto a otra entre magnitudes físicas, químicas, financieras y geométricas, entre otras. Esto se articula con representaciones de modelos funcionales de variadas formas, para apoyar el análisis y la resolución de problemas con funciones reales de una variable real. Hasta este momento se puede ver que el concepto de función en las matemáticas superiores es retomado de las enseñanzas precedentes y tratado en nuevas extensiones (polinómicas, racionales, algebraicas, trascendentes y por partes o secciones) de este concepto. Son ampliadas las formas de representaciones y se profundiza en el análisis de las funciones. La finalidad del trabajo con funciones es interpretar, modelar y resolver problemas en la vida práctica y profesional del estudiante.
SIGNIFICADO EPISTÉMICO (PRETENDIDO) DEL CONCEPTO FUNCIÓN EN LOS LIBROS DE TEXTOS
En la búsqueda de configuraciones epistémicas, nuestro estudio analiza una muestra de libros de textos básicos y complementarios que tradicionalmente han sido usados en la asignatura Matemática I en las carreras de ingeniería, los cuales presentamos en la Tabla 2. Sin embargo, analizamos el libro 1 por considerar que su uso es general en todas las carreras de ingeniería, además de que presenta novedosas representaciones, aplicaciones y problemas e introduce el uso de los asistentes matemáticos. Nos centramos en el análisis de las prácticas matemáticas propuestas en dichos libros de texto, en los capítulos dedicados al estudio del concepto función real de una variable real.
Tabla 2 Listado de los textos tradicionales de matemática usados en la enseñanza del concepto de función.
| Textos básicos de matemáticas en las carreras de ingeniería |
| 1 Stewart, J. (2006). Cálculo con trascendentes tempranas. México: International Thomson Editores |
| 2 Rodríguez, R. (1989). Cálculo diferencial e integral. Cuba: Pueblo y Educación. |
| 3 Berman, G. N. (1989). Problemas y ejercicios de análisis matemático. Cuba: Pueblo y Educación. |
| 4 Piskunov, N. (1977). Cálculo diferencial e integral. Moscú: Editorial Mir. |
| 5 Demidovich, B. (1985). Problemas y ejercicios de análisis matemático. Moscú: Editorial Mir. |
| 6 Kudriávtsev, V., Demidovich, B. (1989). Breve curso de matemática superior. Moscú: Editorial Mir. |
| 7 Ayres, F. (1989). Cálculo diferencial e integral. Teoría y compendio de problemas de cálculo diferencial. México: Libros McGraw-Hill. |
Para comparar los significados globales del concepto de función con los que se pretenden en las carreras de ingeniería, utilizamos la noción de configuración epistémica dada por Godino, Bencomo, Font & Wilhelmi (2006), representada en la Figura II. Esta configuración muestra los principales componentes epistémicos históricos, así como sus contenidos y relaciones, que se utilizan en la construcción del concepto función real de una variable real, en el proceso de enseñanza y aprendizaje. Solo que se reconfigura, debido al nivel de enseñanza y a la introducción del uso de computadoras en la actualidad, que permiten la introducción y el uso del lenguaje, procedimientos, entre otros elementos computacionales. Esta noción permite identificar y describir sistemáticamente los objetos matemáticos primarios (problemas, elementos lingüísticos, conceptos, proposiciones, procedimientos y argumentos) puestos en juego durante la solución de las prácticas matemáticas propuestas.
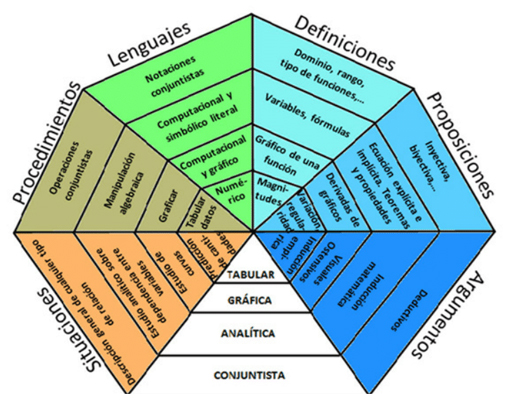
Configuraciones epistémicas
Figura 2 Representación de la configuración epistémica históricamente utilizada por textos y programas de matemáticas en la enseñanza del concepto de función real de una variable real.
El libro Cálculo con trascendentes tempranas, considera dos aspectos didácticos principales para el estudio de las funciones reales de una variable real. El primero va dedicado a los tipos de definiciones y representaciones que se orientan. El segundo trata la resolución de problemas con el uso de las representaciones y definiciones propuestas.
Se abordan cuatro tipos de situaciones/problemas: 1) Situaciones/problemas que plantean alguna relación conjuntistas entre magnitudes de naturaleza geométrica, física, etc., que buscan establecer correspondencias; 2) Situaciones/problemas (resueltos) que ejemplifican, sistematizan y profundizan el uso de las representaciones y definiciones de las funciones, sus propiedades generales y particulares y la aplicación de modelos analíticos; 3) Situaciones/problemas que analizan gráficas (curvas) de mayor composición y comportamientos diversos para determinar propiedades generales y particulares, al igual que a la interpretación de magnitudes. 4) Situaciones/problemas que utilizan principalmente tablas para realizar análisis e interpretaciones, como también conversiones entre las representaciones funcionales. Se introducen conceptos/definiciones relacionados con las clasificaciones de funciones polinómicas, racionales, algebraicas, trascendentes, y el concepto de función por parte y/o por secciones. Se tiene en cuenta que tal concepto de función es utilizado para introducir otros como función continua y derivable. Además de tales definiciones, se dedican tópicos al análisis de estas funciones, con ejemplos variados y argumentaciones que proporcionan un análisis sólido para la solución de tareas y problemas con funciones.
Entre las propiedades/proposiciones que se introducen podemos señalar las propiedades sobre las operaciones con funciones, las transformaciones sobre las funciones, nociones del comportamiento asintótico de una función, el estudio de propiedades particulares y generales de funciones no elementales, por ejemplo su forma gráfica. Son ampliadas las propiedades y proposiciones sobre las funciones compuestas, en cuanto a su determinación y su análisis. Hacemos distintivo en cuanto a los conceptos, propiedades y proposiciones que estos elementos del conocimiento matemático guardan gran relación en el tema de funciones, pues son la base de los procedimientos para el análisis y la interpretación de las mismas.
El análisis y la interpretación de funciones requieren, en este caso, el uso de
procedimientos tanto algorítmicos como heurísticos, apoyándose frecuentemente las
operaciones con funciones con el uso de asistentes matemáticos. Tal es el caso del
cálculo de valores funcionales, de inversas y la representación gráfica, entre
otras. Por tal razón involucramos el trabajo con funciones en este tema dentro de la
resolución de problemas, pues para graficar a lápiz y papel una función cuadrática
basta con conocer un algoritmo, pero para graficar una función
El principal argumento que podemos señalar radica en las justificaciones dadas a la inclusión de conceptos/definiciones o proposiciones, ejemplificación y explicaciones de técnicas a seguir, y el uso de conceptos/definiciones y proposiciones. Además, en la resolución de los distintos problemas son necesarias argumentaciones deductivas y visuales.
Dentro de las características fundamentales de este texto se encuentra la extensión del estudio del concepto de función, la variedad de representaciones funcionales, donde algunas son sistematizadas, se profundizan y otras son ampliadas, como es el caso de las funciones por partes. La propuesta de tareas con el uso de asistentes matemáticos es mucho más eficaz para la comprensión de los conceptos y propiedades, y la realización de tareas con tales elementos cognitivos del aprendizaje.
La Tabla 3 muestra el tipo de conversión que se activa (significados pretendidos y personales) entre las representaciones de una función, en la resolución de los campos de problemas que hemos considerado en este libro de texto, tanto en el planteamiento del problema, como en su solución, así vamos a interpretar la información que nos brinda. Por ejemplo, la celda marcada con una x indica que el libro de texto considera problemas que requieren la conversión entre los distintos registros semióticos que se mencionan en la tabla por cada campo de problemas. Si un problema plantea representar gráficamente una función algebraica dada su ecuación, es un problema que requiere la conversión de analítica a gráfica. Las celdas que poseen color indican que el proceso de conversión no se aplica por una razón lógica, es la misma representación y solo se ejecuta un tratamiento. Las celdas sin selección ni color nos muestran pocos ejemplos y tareas dirigidas en este sentido.
Tabla 3 Muestra en forma matricial las principales conversiones que se realizan en la solución de problemas y que forman parte de los significados que se pretenden en la enseñanza del concepto función.
| Campo de problemas (CP) | Representaciones para f(x) | |||||||
| Emergentes | Verbal | Gráfica | Analítica | Tabular | Secciones | Computacional | ||
| Previas | ||||||||
| CP1: Determinación de relación entre magnitudes (establecer reglas o leyes). | Verbal | x | x | x | ||||
| Gráfica | x | x | x | |||||
| Analítica | x | x | x | |||||
| Tabular | x | x | x | x | ||||
| Secciones | x | x | x | |||||
| Computacional | x | x | x | |||||
| CP2: Cálculo y estimación de valores funcionales. | Verbal | x | ||||||
| Gráfica | x | |||||||
| Analítica | x | |||||||
| Tabular | x | |||||||
| Secciones | x | |||||||
| Computacional | x | |||||||
| CP3: Representación de funciones en situaciones intra-matemáticas. | Verbal | x | x | |||||
| Gráfica | x | x | x | |||||
| Analítica | x | x | x | |||||
| Tabular | x | x | x | |||||
| Secciones | x | x | ||||||
| Computacional | x | x | x | x | ||||
| CP4: Modelación de situaciones prácticas mediante funciones. | Verbal | x | x | |||||
| Gráfica | x | x | x | |||||
| Analítica | x | x | x | |||||
| Tabular | x | x | x | |||||
| Secciones | x | x | ||||||
| Computacional | x | x | x | x | ||||
| CP5: Representación de funciones en máquinas computadoras u otros dispositivos electrónicos. | Verbal | |||||||
| Gráfica | ||||||||
| Analítica | x | x | x | |||||
| Tabular | x | x | ||||||
| Secciones | x | |||||||
| Computacional | ||||||||
Ejemplos de los significados que se pretenden en este libro de texto por campos de problemas
Después de observar las entradas en la Tabla 3, según la interpretación que le hemos dado luego de la revisión del libro de texto, apreciamos cómo las entradas en dicha tabla están distribuidas en tan solo algunas casillas. Si bien es cierto que los libros estudiados proponen varios sistemas de representación, también lo es el vínculo entre ellos, y el tratamiento específico que lleva la actividad de aprendizaje que se realiza en forma de tareas o ejercicios como caso particular de esta.
Observemos que no siempre se logra tener una matriz simétrica de entrada de valores en cada cuadrante de colores diferentes asociados a cada campo de problemas, lo que refleja que la conversión entre registros semióticos en el texto sobre el tema de funciones reales de una variable real no es bidireccional, lo que puede ser una alerta de que los docentes deben dirigir el dominio de los significados institucionales que los planes de estudio y programas proponen. Se reconoce la dificultad de diseñar actividades matemáticas que, en conjunto, utilicen todas las posibles conversiones semióticas exhibidas en la tabla; el énfasis en solamente algunas, como la relación analítica-gráfica o viceversa puede afectar la atribución de significados, de manera que algunos sean olvidados y se refuercen otros.
RESULTADOS Y CRITERIOS OBTENIDOS
Persiste aún en la enseñanza del concepto de función la prevalencia de significados algebraicos y gráficos. Sin embargo, se incrementa el trabajo con funciones numéricas y verbales en problemas prácticos que apoyan la comprensión y significatividad del concepto, mediante un cubrimiento más completo de sus formas de representación. En este sentido, es necesario que tales significados sean sistematizados durante la actividad matemática y la práctica-profesional que se realiza vinculada con el concepto.
Criterio 1: La inserción de múltiples significados del concepto función en la instrucción facilita y complementa el diseño de actividades matemáticas vinculadas con la profesión
De acuerdo con lo planteado por Pino-Fan, Guzmán, Font & Duval (2017), la representación semiótica que se moviliza en cada contexto (algebraico, gráfico, numérico) es amplia, pues son incorporados gráficas, ecuaciones, tablas y elementos lingüísticos, entre otros elementos. Para esto, los procedimientos, métodos, estrategias, etc., que se dirijan al tratamiento deben ser generales, de manera que lo particular de cada representación pueda ser relacionado con lo esencial del concepto.
Criterio 2: La conversión de registros semióticos en el trabajo con funciones es considerada un procedimiento heurístico esencial para el entendimiento y la solución de tareas y ejercicios, como forma de resolver problemas.
Criterio 3: En el trabajo con funciones la conversión y el tratamiento es el componente esencial para la comprensión y la resolución de ejercicios
El análisis de propiedades de las funciones en la enseñanza se realiza fundamentalmente sobre la base de distinguir propiedades generales y particulares en sus más diversas formas de representación. Esto implica que debe procurarse mediante herramientas didácticas que permiten la racionalidad del pensamiento matemático, tales como la interpretación representacional del concepto y sus propiedades.
Criterio 4: El análisis funcional como actividad fundamental del trabajo con funciones requiere del uso racional de acciones de didácticas, las cuales pueden ser: la descripción, la interpretación, la variación de condiciones, la modificación, etc., que conlleven a la determinación de propiedades.
Los ejemplos mostrados en cada campo de problemas han sido objeto de evaluación en los alumnos que cursan las carreras de ingeniería industrial, mecánica y ciencias alimentarias, que conforman una muestra de 128 estudiantes. El propósito de la evaluación en cada uno de estos problemas consistió en valorar la obtención de la conversión y la ejecución del tratamiento, de manera que se tenga en cuenta que son dos procesos paralelos y verticales que ejecuta el sujeto que aprende cuando se enfrenta a los problemas que hemos descrito. De manera general, pudimos determinar que los resultados de los problemas no son favorables cuando se centran en la obtención de registros de forma gráfica y analítica a partir de otros, pues solo 48% de los estudiantes logra resultados satisfactorios en este sentido. Sin embargo, la motivación por realizar tareas de este tipo mejora, pues constituye algo novedoso en el conocimiento de las funciones para el quehacer del ingeniero. Los mejores resultados, 62%, se obtienen cuando los alumnos realizan tareas donde interactúa el registro analítico con el gráfico, o viceversa.
De manera global, en este análisis sobre las prácticas operativas de los estudiantes se manifiesta que los algoritmos utilizados en el tratamiento son usados de forma eficiente, pero después de que el profesor ofrece niveles de ayuda, con baja efectividad para el desarrollo cognitivo del estudiante. Por tal motivo, es necesario que en las tareas que realicen los alumnos evidencien el trabajo eficiente con los componentes epistémicos, sobre sus interpretaciones y justificaciones en el conocimiento de las funciones reales de una variable real.
CONCLUSIONES
Hemos presentado un análisis didáctico de los principales significados epistémicos que se pretenden en los planes y programas de estudio, al igual que en libros de texto, para la enseñanza de las matemáticas en las carreras de ingeniería. Los significados epistémicos que están presentes de manera frecuente en el trabajo con funciones son los 6 expresados en la Tabla 3, aunque existen otros significados como los diagramas de flechas y de máquinas, que son solamente ilustrativos para comprender el concepto de función. También se presentan algunos resultados en el orden cognitivo, que desarrollan los estudiantes. El análisis estuvo apoyado en los componentes que brinda y que caracterizan la idoneidad epistémica en el trabajo con funciones. De este análisis resultó descrito un campo de problemas que involucra a cada uno de los componentes de la idoneidad epistémica, los cuales -relacionados con dichos componentes-, conforman un sistema de prácticas que se manifiestan en la enseñanza y el aprendizaje del concepto de función.
Como aspecto importante a tener en cuenta desde la perspectiva de nuestro análisis, está que los registros semióticos asociados al concepto de función articulan con el objeto y con los diferentes tipos de problemas; además de que profundizan el trabajo en la conversión y el tratamiento entre variadas formas de representaciones. Esta articulación forma parte de las prácticas pretendidas y operativas en el proceso de enseñanza y aprendizaje. Cuando los campos de problemas que involucran a los componentes y sus significados pretendidos - relativos al concepto de función en nuestro caso- se relacionan con las representaciones (verbal, numérica, analítica, gráfica, entre otras), es posible evidenciar el comportamiento de las conversiones entre representaciones.
Los campos de problemas que han sido determinados no solo constituyen sistemas de prácticas que se trabajan desde el proceso de enseñanza de las matemáticas en las carreras de ingenierías, forman también la actividad matemática que llevan a cabo dichos estudiantes cuando se enfrentan a las tareas con el concepto de función y donde, a su vez, encuentran las mayores dificultades. A modo de resumen, se tiene que en la enseñanza y el aprendizaje del concepto de función en las carreras de ingenierías, los docentes y alumnos encuentran un aumento de:
Los registros semióticos sobre la representatividad del concepto, incluido de forma ascendente el computacional, así como su complejidad.
Los procesos de conversión y tratamiento entre representaciones reflejados por campos de problemas.
Las clasificaciones, procedimientos de solución, habilidades, proposiciones, entre otros elementos, que conforman el significado epistémico idóneo para realizar tareas de aprendizaje.
De modo general, consideramos que la elección de tareas matemáticas que articulen los campos de problemas y los significados matemáticos es crucial para promover la idoneidad epistémica y cognitiva del aprendizaje significativo del concepto función real de una variable real.











 text new page (beta)
text new page (beta)