1. Introducción
La enseñanza de la Matemática para carreras profesionales plantea grandes desafíos en los profesores y las universidades desde hace años, pues las tendencias marcan que debería enseñarse de manera contextualizada y a través de la resolución de problemas. Pita, Añino, Ravera, Miyara, Merino y Escher (2011) expresan que:
Se ha popularizado la idea de que la Matemática está en todos lados, pero esto no es tan taxativo. Dicho de otra manera, no es simplemente que está sino que hay que hallarla, aprovechando sus métodos y procedimientos en la formación del estudiante. (p. 9).
En Argentina, la Comisión Nacional de Evaluación y Acreditación Universitaria establece que el plan de estudios de cada carrera debe estar adecuadamente integrado, con objeto de lograr el desarrollo de las competencias necesarias para la identificación y solución de problemas abiertos. Estos se entienden como aquellas situaciones reales o hipotéticas que plantean los profesores a sus estudiantes, cuya solución demanda la aplicación de los conocimientos de las Ciencias Básicas y de las Tecnologías, y son considerados un indicador de la calidad educativa que brinda la Universidad (Ministerio de Educación, 2001).
A su vez, numerosos trabajos referidos a la enseñanza de la Matemática proponen algunos principios y lineamientos generales, con la finalidad de lograr profesionales idóneos. Así, por ejemplo, Pita et al. (2011: 10) expresan que "nuestra meta es una enseñanza atractiva que mejore las condiciones de aprendizaje, apuntado a formar un estudiante hábil en la identificación y apto para la formulación de problemas". En tanto Jóver (2003: 85) enfatiza que "cuando se explora la resolución de problemas por métodos heurísticos emerge un variado paisaje de técnicas que se proponen como adecuadas". Méndez (2010: 2-3), por su parte, sostiene que las Ciencias Básicas impulsan al estudiante a "ser creativo e innovador, situación indispensable para atender a los problemas del mundo real a los que se enfrentará profesionalmente".
No obstante, la problemática sobre el tipo de actividades y problemas que se deberían proponer a los estudiantes, en la formación matemática universitaria, pareciera ser aún una dificultad por superar. Nieto (2004) argumenta que para alcanzar estos objetivos se deben trascender los procesos de enseñanza y aprendizaje basados en la exposición magistral en el aula, y poner a los estudiantes en contacto con la realidad que nos rodea.
Hasta hace algunas décadas lo más importante era saber Matemática, y resultaba suficiente para que el docente pudiera enseñar esta ciencia contar sólo con conocimientos disciplinares. Sin embargo, hoy en día, según lo expresan Pochulu y Rodríguez (2012):
Al profesor de Matemática se le pide o exige un nuevo comportamiento profesional, una nueva actitud hacia los alumnos; un conocimiento y habilidades pedagógicas flexibles según las distintas situaciones y contextos educativos; un conocimiento de la disciplina en sí y el conocimiento didáctico asociado a ella. Asimismo, se espera y pretende que: logre impulsar y motivar el trabajo de los alumnos conduciéndolos a la reflexión; domine aspectos sociales y emotivos de los alumnos; sea hábil en la generación de entornos de aprendizajes matemáticamente ricos y enriquecedores; diseñe modelos que se adapten a las inciertas y cambiantes condiciones de aprendizaje que se dan en las clases de Matemática, y sepa preparar a sus alumnos, ya sea para una integración y participación en el mundo del trabajo, o para la continuidad de estudios superiores (p. 9).
Teniendo en cuenta la problemática planteada, se propuso trascender las clases habituales de Matemática en la carrera de Profesorado en Física de la Universidad Nacional de San Juan (Argentina), y se decidió trabajar con resolución de problemas y nuevos recursos. Si bien es complejo dar un concepto de "problema", pues son numerosos los autores que han dedicado esfuerzos para definirlo o caracterizarlo, con múltiples acepciones, se adhiere a lo expresado por Rodríguez (2012) cuando resalta el hecho de que:
Uno define el concepto de problema para un sujeto, y no simplemente la noción de problema. Esto expresa que lo que para un individuo resulta ser un problema, bien podría no serlo para otro. Esta relatividad al sujeto es una característica inherente al concepto y a la vez empieza a poner de manifiesto la complejidad de su uso en el aula (p. 155).
En este trabajo sólo se reporta una tarea, que se describe y fundamenta desde su diseño hasta la implementación, utilizando como marco teórico y metodológico:
La noción de escenario de investigación de Skovsmose (2012) desde la Educación Matemática Crítica (EMC), quien describe distintas tipologías de clases de Matemática y propone el trabajo en la clase organizando actividades que se montan sobre escenarios de investigación.
Algunos elementos de la Teoría de Situaciones Didácticas (TSD) de Brousseau (1986), en lo que hace a características de la tarea, momentos de la clase, rol del alumno y del profesor en la gestión de la clase.
Los criterios de idoneidad didáctica que propone el Enfoque Onto-semiótico del conocimiento e instrucción matemática (EOS) de Godino, Batanero y Font (2007), para analizar procesos de enseñanza y aprendizaje para implementar e implementados. De acuerdo con Godino, Bencomo, Font y Wilhelmi (2006), la idoneidad didáctica es la articulación coherente y eficaz de las distintas dimensiones implicadas en los procesos de estudio matemático: epistémica, cognitiva, interaccional, mediacional, emocional y ecológica.
En la descripción del diseño e implementación de la tarea se introducirán los elementos teóricos con los cuales se fundamenta y analiza la propuesta didáctica.
2. El diseño de la actividad
El conocimiento para trabajar en la clase y con los alumnos corresponde al eje "geometría y medida" y, en particular, se busca que emerja el concepto de área de la pirámide recta, a partir de su desarrollo plano. Con este propósito se buscó organizar una situación didáctica, de acuerdo con la TSD, impregnada de intencionalidad didáctica, para lograr el aprendizaje por parte del alumno. Para ello se provocó "una tensión entre las anticipaciones y las decisiones que se puedan tomar, con la finalidad de que emerja un nuevo conocimiento" (Barreiro y Casetta, 2012: 18). Entendemos que si el alumno asume la responsabilidad de resolver el problema o la tarea sin percatarse de la intencionalidad didáctica, la situación se convierte en a-didáctica.
Los objetivos generales que se propusieron para la clase fueron: (a) Comprender el concepto de área de una pirámide mediante su desarrollo plano, (b) Identificar y utilizar procedimientos matemáticos para construir pirámides rectas a partir de condiciones iniciales, y (c) Utilizar el lenguaje algebraico para generalizar propiedades aritméticas y geométricas.
De manera más específica se buscó propiciar la exploración y el descubrimiento, dando espacio para que aparezcan conjeturas, puestas a prueba y argumentaciones, tal como lo sugiere Skovsmose (2012) para escenarios de investigación. Skovsmose (2012: 111) le da el nombre de "escenario de investigación a una situación particular que tiene la potencialidad de promover un trabajo investigativo o de indagación" en los estudiantes. Este ambiente de aprendizaje viene a contraponerse totalmente al paradigma del ejercicio que ha caracterizado tradicionalmente las clases de Matemática.
Si se tienen en cuenta los dos paradigmas que pueden dominar las clases de Matemática: del ejercicio o de investigación y, además, se consideran como referencia contextos de la Matemática pura; de la semirrealidad o situaciones de la vida real se tendrían los siguientes ambientes de aprendizaje (enumerados del 1 al 6):
Skovsmose expresa que la educación matemática se mueve solamente en los ambientes (1) y (2) de la Tabla 1, y sugiere moverse por los restantes; también sostiene que en los escenarios de investigación los estudiantes están al mando, pero se constituyen como tal si aceptan la invitación, la cual depende del profesor. Asimismo, "lo que puede constituirse en un escenario de investigación para un grupo de estudiantes en una situación particular puede no convertirse en una invitación atractiva para otro grupo" (Skovsmose, 2012: 114-115). Advierte, además, que un escenario de investigación debe promover en los estudiantes la formulación de preguntas, la búsqueda de explicaciones, la posibilidad de explorar y explicar las propiedades matemáticas, etc. Todo esto está condicionado por el tipo de problema o actividad que se les proponga y, obviamente, la gestión de la clase que realice el profesor.
La tarea se buscó centrarla en un escenario de investigación de la semirrealidad y, para el enunciado de la consigna, se tuvo en cuenta uno de los criterios que proponen Rodríguez Pochulu y Ceccarini (2011: 466) para organizar la enseñanza de Matemática Superior, buscando favorecer la comprensión: "Presentar preguntas o cuestionamientos directrices amplios, que exijan, para su análisis, apelar a contenidos matemáticos usualmente separados en distintos campos (geométrico, analítico, algebraico, etc.)".
Ahora bien, teniendo presente los principios de la TSD en Sadovsky (2005), los cuales orientaron el diseño e implementación de la actividad, se decidió que la resolución de la tarea admitiera situaciones de acción, formulación y validación. Para ello fue necesario que la tarea, en un análisis a priori, permitiera estas instancias. En este sentido se recurrió a algunos criterios enunciados por Pochulu, Font y Rodríguez (2009), los cuales tienen la finalidad de facilitar que la tarea promueva procesos matemáticos relevantes y variados, como el de argumentación y el de modelización, y que guarden correspondencia con el tipo de actividades que se espera sean formuladas en el marco de la TSD. Estos criterios fueron:
La tarea debe admitir más de un camino posible de resolución, para que genere diferentes tipos de actividad matemática en los alumnos, aparezcan distintas conjeturas y promueva instancias de validación. Según Pochulu (2013) el término "camino" alude a una forma o estrategia de resolución empleada para obtener una respuesta válida, según las condiciones de la situación propuesta.
En la consigna no deben explicitarse ayudas o sugerencias de caminos posibles a seguir para la resolución, como así tampoco información que asegure existencia o unicidad de algo buscado.
La tarea debe requerir que se justifiquen las elecciones que efectúan los alumnos, así como las que se rechazan, en tanto se busca promover un proceso matemático relevante como es el de argumentación.
El propósito de la tarea debe ser algo matemático y no referido al uso de software o manejo de comandos específicos.
Las actividades involucradas en la tarea fueron pensadas para ser desarrolladas en grupo (otra característica distintiva de la TSD) durante 120 minutos. Formó parte del contrato didáctico que los estudiantes expondrían sus conclusiones de manera oral ante el resto de la clase.
La consigna entregada a los estudiantes, quienes debían trabajar en grupo, fue la siguiente:
Se ha decidido confeccionar souvenirs para entregar en la fiesta de egresados, los cuales debieran tener forma de pirámide recta, en alusión al logo de la institución educativa, de modo tal que la arista de su base cuadrada mida 6 cm. Analizar y justificar si es posible construir alguna pirámide utilizando una lámina de cartulina de 9 cm por 10 cm.
Superada la primera instancia de trabajo de los estudiantes, se les solicitó que construyeran un prototipo de souvenir, de acuerdo con las especificaciones que habían encontrado y justificado.
El análisis a priori de la tarea muestra que:
El problema es de carácter extra-matemático, dado que es una situación propia de la disciplina que se encuentra inmersa en un contexto real. Como implica hacer cálculos y construir un prototipo, involucra procedimientos algorítmicos y constatación empírica.
Su formulación no indica formas de modelización, puesto que no habla de ecuaciones, inecuaciones o gráficos. Tampoco asegura la existencia y/o unicidad de la solución; más aún, admite más de una resolución, y la estrategia elegida proporcionará distintas respuestas al respecto.
La intencionalidad didáctica conlleva a abordar el área de una pirámide recta desde la deducción, promoviendo la producción de argumentos para validar las respuestas.
Los estudiantes cuentan con los conocimientos previos que demanda la tarea, entre ellos: clasificación y elementos de la pirámide recta, construcciones geométricas elementales, clasificación de triángulos, Teorema de Pitágoras y áreas de figuras planas.
Cumple con la cualidad de "ser problema", pues si bien es una cuestión relativa al sujeto que resuelve, el alumno no sabe exactamente cuál es el camino que debe seguir para resolverlo. Esta incertidumbre lo lleva a explorar distintas estrategias no formalizadas para acercarse a la resolución, las cuales no necesariamente son exitosas o válidas desde el punto de vista matemático.
Para garantizar que la implementación de la clase tuviera los rasgos que impone la TSD y al mismo tiempo se contara con elementos suficientes para realizar una valoración de la idoneidad didáctica de los procesos de enseñanza y aprendizaje, de acuerdo con los criterios propuestos por el EOS, se realizó:
La anticipación de las resoluciones posibles que tendría la tarea, la descripción de los errores y dificultades que se les presentarían a los alumnos, y las respuestas inesperadas o inacción ante una actividad.
La descripción del modo en que se gestionaría la clase ante las instancias mencionadas en el ítem anterior, expresadas como diálogos hipotéticos entre el profesor y el alumno.
Puesto que desde la TSD el rol del profesor es fundamental y le corresponde no sólo la devolución del saber sino la del problema a los alumnos, para la descripción de la gestión de la clase se tuvieron en cuenta los siguientes criterios, a fin de llevar a cabo las intervenciones docentes:
Intervenir haciendo reflexionar al alumno mediante preguntas que no contuvieran información sobre los caminos que debía seguir en la resolución de la tarea. Se busca que piense sobre lo realizado y analice los procedimientos empleados en la actividad, más que llevarlo al modo en el cual el profesor tiene pensada la resolución.
Evitar decir directamente si la resolución es o no correcta, pues se estaría haciendo responsable el profesor de la resolución del problema. Por el contrario, pedir explicaciones para tratar de entender el modo de pensar que lo llevó hasta ahí y, al mismo tiempo, se le devuelva la responsabilidad de resolución del problema al alumno.
Evitar pedir sólo explicaciones cuando la respuesta del alumno es incorrecta, pues se pretende ayudar a que validen sus producciones y puedan sostener argumentos convincentes.
El objetivo de tener en cuenta estos criterios buscó planificar intervenciones que tuvieran mayor idoneidad cognitiva, afectiva e interaccional, siguiendo, al mismo tiempo, los indicadores que propone el EOS. A su vez, se lograría ayudar a aumentar la autoestima de los alumnos facilitando procesos cognitivos y meta-cognitivos que son indicadores de estas cuatro idoneidades.
Además, las intervenciones docentes apuntan no sólo a trabajar con los errores, sino también a inducirlos para que propongan modelos matemáticos a partir de los cuales concluyan que las pirámides que se pueden construir con los requisitos solicitados son todas aquellas cuyas medidas de sus apotemas varíen en el intervalo de números reales . Esto es relevante cuando se encuentren en situaciones de formulación y validación.
Por supuesto, no se espera que las interacciones se den tal cual se describen, pues las mismasse readaptan en función de la experiencia del profesor en la gestión de la clase y las respuestas que va recibiendo de los alumnos.
Conforme los conocimientos previos de los alumnos, se puede asumir que tendrán en cuenta que las caras de la pirámide recta son triángulos. No obstante, no se espera que recuerden que se trata de triángulos isósceles, cuyos lados congruentes son las aristas del cuerpo en cuestión.
Es razonable suponer entonces que las estrategias que podrían emplear partan de descomponer la pirámide en las figuras planas que componen su frontera, para luego calcular sus áreas. De esta manera, necesitarán hallar la altura del triángulo que forma la cara de la pirámide.
2.1 Caminos de resolución
A continuación se muestran algunas resoluciones con sus dificultades y los modelos de diálogos hipotéticos, mediante los cuales se pretende que el profesor devuelva el problema a los alumnos y ayude con los procesos de reflexión.
Cabe aclarar que los caminos no están sujetos a un orden secuencial, e incluso un mismo grupo podría incurrir en más de uno. Para que la situación a-didáctica se produzca, el estudiante debe lograr trabajar de forma independiente. Puede estar latente dentro de la situación didáctica; surge cuando el problema propuesto por el profesor le permite al alumno actuar de manera distinta en cada aproximación, aunque hay que tener presente que no se da siempre. Para garantizar que ocurra, es imprescindible que se incluya en la diagramación de la situación didáctica. En esta fase el profesor interviene estratégicamente solo para brindar alguna información o realizar preguntas, y es lo que se intenta plasmar en las descripciones de los diferentes caminos e intervenciones docentes para gestionar la clase.
Camino 1: Consideran que las caras de la pirámide son triángulos escalenos
En este caso, los alumnos no pueden modelizar matemáticamente la situación. Por tanto, la intervención está encaminada a que revisen qué datos no consideraron.
Profesor: ¿Cuáles son las figuras que necesitan para construir la pirámide?
Alumnos: Un cuadrado de 6 cm de lado y cuatro triángulos.
Profesor: ¿Qué otro dato tienen?
Alumnos: Las dimensiones de la lámina y que la pirámide es recta.
Profesor: ¿Qué significa para ustedes pirámide recta?
Alumnos: No lo recordamos.
Profesor: Pueden revisar ese concepto buscando información, y luego plantear un camino de resolución.
Camino 2: Sólo utilizan estrategias de tanteo numérico
Los alumnos solamente dan valores a la medida de la apotema teniendo en cuenta que son números positivos, y que el área total del cuerpo no debe superar el área de la lámina. Además, pueden considerar que los valores deben ser factibles de medir con útiles de geometría.
Supongamos que organizan sus cálculos mediante la Tabla 2 siguiente:
Luego, establecen que todos los valores de la apotema en los que el área de la pirámide es menor o igual a 90, son ejemplos de medidas con las cuales se pueden elaborar construcciones.
En la intervención, el docente utiliza la tabla precedente para inducirlos a plantear una inecuación e intentar encontrar caminos para formular y validar sus apreciaciones. Asimismo, los cuestionará sobre si todos los valores que consideraron para la apotema cumplen con los requisitos necesarios para construir la pirámide.
Profesor: ¿De qué manera podrían expresar una conjetura que resuma lo que han estado explorando?
Alumnos: Deberíamos escribir, en lugar de cada valor particular. De este modo nos quedaría planteada una inecuación.
Profesor: ¿Cuál es el conjunto solución?
Alumnos: Al resolverla nos quedan todos los valores pertenecientes al intervalo
Profesor: Y eso, ¿qué significa en el contexto de este problema?
Alumnos: Significa que la medida de la apotema es menor o igual que
Profesor: Entonces, ¿puede tomar valores negativos?
Alumnos: Claro que no, ya que se trata de la medida de un segmento. Es decir que, en definitiva, la respuesta es el intervalo
Profesor: ¿Se les ocurre alguna forma de verificar que la medida de la apotema varía entre los valores de este conjunto?
Alumnos: Tendríamos que construir una.
Profesor: ¿Será suficiente realizar algunas construcciones particulares para asegurarlo?
Alumnos: No, tendríamos que hacer todos los casos. Pero, ¡eso es imposible!
Profesor: ¿Pueden usar otra estrategia?
Alumnos: Tendríamos que analizar otros factores que condicionan la construcción, por ejemplo, las medidas de las aristas laterales o las de la base o la de la altura de la pirámide.
Profesor: ¡Muy buena idea! Piensen de qué modo pueden relacionarlos.
Camino 3: Consideran que las caras de la pirámide son triángulos equiláteros
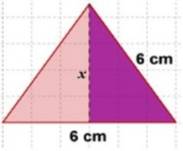
En este caso, tienen la información necesaria para aplicar el Teorema de Pitágoras, de acuerdo con los datos de la Figura 1.
Obtienen que la altura del triángulo es 5.1 cm aproximadamente. Así, pueden calcular el área total de la pirámide y compararla con el área de la lámina, concluyendo que no es posible realizar alguna construcción.
La intervención apunta a cuestionar la estrategia empleada y a que consideren otras posibilidades para resolver la actividad.
Profesor: ¿Cuáles son las razones que los llevaron a pensar que la arista lateral de la pirámide mide 6 cm?
Alumnos: El único dato que nos dieron es la medida de la arista de la base de la pirámide, y esta coincide con uno de los lados del triángulo.
Profesor: Entonces, ¿con qué tipo de triángulo trabajaron en definitiva?
Alumnos: Con uno que tiene todos sus lados congruentes, o sea, con un triángulo equilátero.
Profesor: ¿Hay algún obstáculo que les impida considerar este tipo de figura plana?
Alumnos: En realidad no hay inconvenientes, pues uno de los requisitos es que la pirámide sea recta. Según su definición, las caras son triángulos isósceles, o sea, son triángulos que tienen al menos dos lados congruentes. Por tanto, nuestro caso cumple con ese requisito.
Profesor: Entiendo los argumentos que están dando, sin embargo, su conclusión es que la pirámide no se puede construir. ¿Existirá alguna forma de solucionar esto?
Alumnos: Tendríamos que admitir que la medida del lado de la base del triángulo no coincide con la medida de los lados de las caras.
Profesor: Intenten encarar la actividad teniendo en cuenta esa característica.
Camino 4: Modelan el problema mediante una ecuación
Los alumnos entienden que hay que utilizar toda la lámina de cartulina para construir la pirámide, y modelan el problema mediante la siguiente ecuación:
Al resolverla, determinan que la altura del triángulo mide 4.5 cm y, por tanto, existe una única pirámide que puede construirse en la lámina.
La intervención está orientada a que revisen si el condicionamiento que impusieron fue pedido en la consigna, y analizar si su modelo matemático seguirá siendo apropiado, en caso de tener que quitarlo.
Profesor: En la vida real, ¿qué significa para ustedes que la diferencia entre el área de la lámina y la suma de todas las áreas de las figuras planas que componen la frontera de la pirámide debe ser igual a cero?
Alumnos: Eso significa que no sobra lámina.
Profesor: Pero, ¿qué pasaría si se equivocan al realizar los cortes de alguna de las figuras?
Alumnos: Esa pieza debería ser reemplazada. Pero eso no sería posible, ya que no tendríamos más material para hacerlo.
Profesor: ¿Existe alguna alternativa para prever ese inconveniente?
Alumnos: Tendríamos que pensar en que no se necesita utilizar toda la lámina.
Profesor: ¿Cómo afectaría eso al modelo matemático que obtuvieron?
Alumnos: Cambiaría, ya que nos quedará planteada una inecuación.
Profesor: Y en ese caso, ¿qué obtendrán como respuesta a la consigna?
Alumnos: Ya sabemos que existe al menos una solución. Entonces, al resolver la inecuación obtendremos infinitos resultados, por lo cual tendremos que ver cuáles son los valores que podrá tomar que nos permitan construir alguna pirámide utilizando la lámina de cartulina.
Camino 5: Modelan el problema mediante una sola inecuación
Consideran que la diferencia entre el área de la lámina y la suma de todas las áreas de las figuras planas que componen la frontera del cuerpo debe ser mayor o igual a cero.
Plantean la siguiente inecuación:

Al resolverla, determinan que pueden construirse infinitas pirámides con apotemas que tengan medidas que sean menores o iguales a . Pero este resultado no tiene en cuenta que el doble de la medida de la apotema de una pirámide recta de base cuadrada tiene que ser mayor que la medida de la arista de su base. De ahí se obtiene que también debe verificarse que:
Profesor: En su trabajo indican que. Esta conclusión en la vida real, ¿es posible?
Alumnos: Sabemos que es una medida, por tanto, es no negativa. Así que
Profesor: ¿Qué relación pueden marcar entre los valores de con respecto a los demás elementos de una pirámide que cumpla con las especificaciones de la consigna?
Alumnos: Es posible que podamos establecer alguna propiedad identificando otros triángulos en el cuerpo.
Profesor: Analicen las opciones que tienen y discutan en el grupo si las relaciones obtenidas afectan o no a su conclusión.
3. La implementación de la tarea
A continuación reseñamos fragmentos de lo recogido de un grupo particular constituido por dos (2) de los quince (15) alumnos que cursaron Análisis Matemático del Profesorado de Física en la Universidad Nacional de San Juan (Argentina) durante el año académico 2014. Este grupo inició la resolución suponiendo que el desarrollo plano de la pirámide debía ocupar toda la superficie de la lámina de cartulina. Por este motivo plantearon una ecuación considerando que la cuarta parte del área de la lámina (descontando el área de la base del cuerpo) tenía que ser igual al área de un triángulo (ver Figura 2). Con los resultados obtenidos pudieron proponer un desarrollo plano de la pirámide. Esto dio paso a la intervención del Camino 4, para inducirlos a que planteen una inecuación.
Durante ese proceso advirtieron, a través de una representación gráfica, que la suma de las medidas de las aristas laterales de la pirámide tenía que ser mayor que la medida de la diagonal del cuadrado de su base. De acuerdo con esta condición descubierta sobre la medida de la arista lateral, escribieron una inecuación, a partir de la cual determinaron la medida máxima que podía alcanzar la apotema del cuerpo.
Enseguida, la docente procedió a interrogarlos sobre el valor mínimo que podía tomar la medida, acorde a lo estipulado en el diálogo del Camino 5. Para dar una respuesta los alumnos dedujeron, gracias a la misma representación gráfica que elaboraron, que la medida de la apotema debía ser mayor que la mitad de la medida de la arista de la base de la pirámide recta de base cuadrada.
Después de determinar el rango de valores que podía tomar la medida de la apotema, usaron un utilitario geométrico (Geogebra 5.0) y obtuvieron otros dos ejemplos de desarrollos planos, optimizando notablemente el tiempo para realizar los gráficos.
Por último, optaron por construir la pirámide que requería toda la superficie de la lámina de cartulina (Figura 2).
Para el cierre de la clase, la docente recuperó lo elaborado por los alumnos y las diferentes estrategias utilizadas para lograr institucionalizar el conocimiento que se buscaba que se manifestara. Es de destacar que al trabajar con la tarea propuesta se logró promover en los alumnos la formulación de preguntas, la búsqueda de explicaciones, la posibilidad de explorar y explicar las propiedades matemáticas, etc.; todo esto estuvo condicionado por el tipo de problema que se les propuso y, obviamente, la gestión de la clase que efectuó la docente.
Para analizar la idoneidad didáctica de todo el proceso de estudio se utilizaron los criterios de idoneidad propuestos por el EOS en Font, Planas y Godino (2010). Los criterios de idoneidad fueron reglas de corrección útiles en dos momentos de la propuesta didáctica que se presenta. A priori, los criterios de idoneidad fueron principios que orientaron acerca de cómo había que hacer el diseño de la tarea y gestionar la clase. A posteriori, los criterios sirvieron para valorar el proceso de estudio efectivamente implementado. A modo de ejemplo, se transcriben sólo dos indicadores de idoneidad.
4. Consideraciones finales
La tarea que se presentó en este trabajo pretendió lograr la construcción y comprensión de saberes matemáticos a partir de los conocimientos previos de los estudiantes. La consigna fue enunciada de modo que tuviesen múltiples formas de plantear, explorar y resolver.
Es fundamental observar que, si bien la consigna es relevante, son las intervenciones del profesor y la gestión de la clase las que complementan la idoneidad didáctica que puede lograr el proceso de estudio. A partir del análisis a priori de la actividad, el docente puede contar con ideas para pensar cómo persuadir a los estudiantes para que reflexionen sobre sus respuestas y, consecuentemente, generen nuevos modelos matemáticos que describan más apropiadamente el problema planteado. Es por ello que le damos mayor importancia a los diálogos hipotéticos antes que a los reales, debido al papel preponderante que juegan en el diseño de la tarea, para gestionar la clase de acuerdo al marco de la Teoría de Situaciones Didácticas.
Las intervenciones intentan, por un lado, llevar a los alumnos a asumir la responsabilidad en la tarea, para así lograr que la situación se torne en a-didáctica y, por otro, a que consigan una respuesta que rebase las fronteras de lo que se les pide en las consignas.
La utilización de marcos teóricos de la Didáctica de la Matemática brinda constructos y herramientas que ayudan a planificar y gestionar una clase para hacer progresar a los alumnos en sus razonamientos matemáticos, propiciando instancias no sólo para trabajar con los errores, sino también para justificar y validar lo realizado.
Asimismo, el trabajo con resolución de problemas y en escenarios de investigación pudo mostrar tanto a profesores como a estudiantes que existen otras maneras de trabajar y hacer Matemática en el aula universitaria. Esta modalidad de trabajo está más próxima a los campos profesionales de las carreras en las que se inscriben los estudiantes, y no se descuidaron los contenidos centrales, que suelen ser preocupación de los profesores.











 text new page (beta)
text new page (beta)