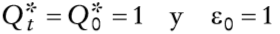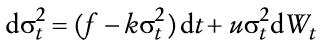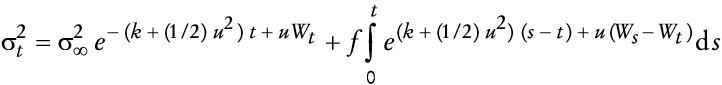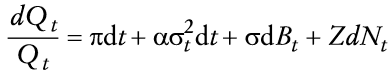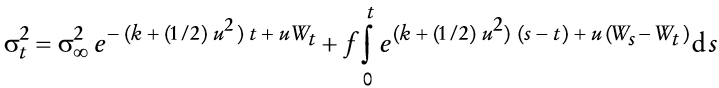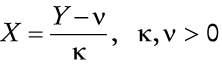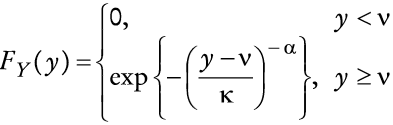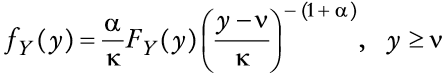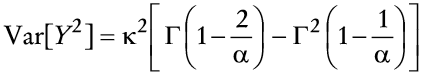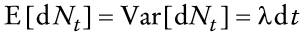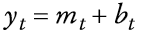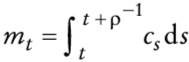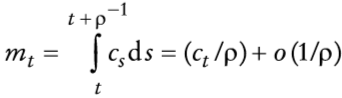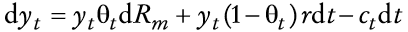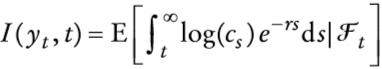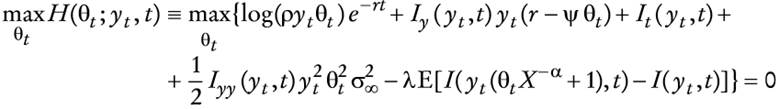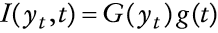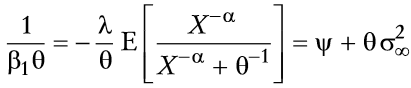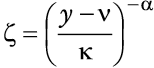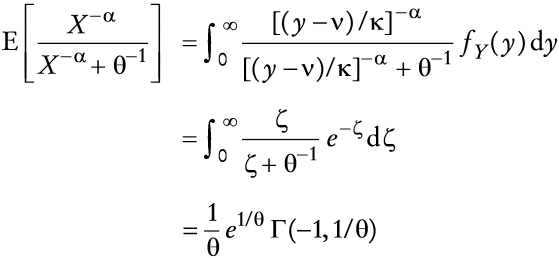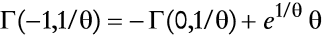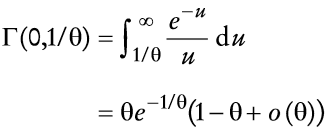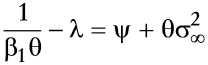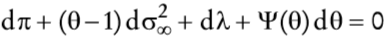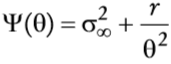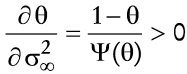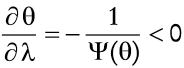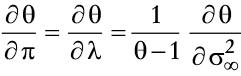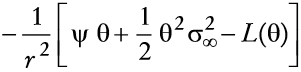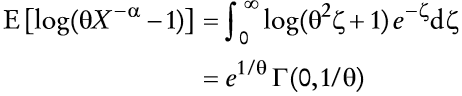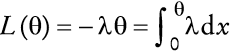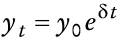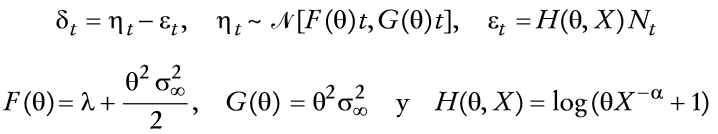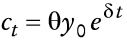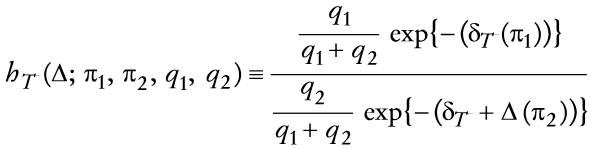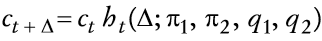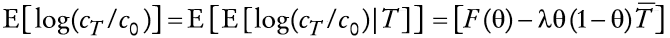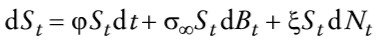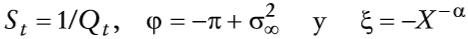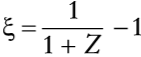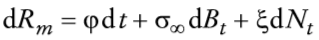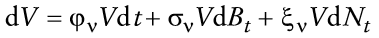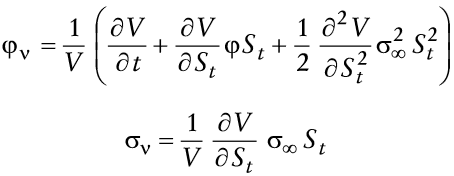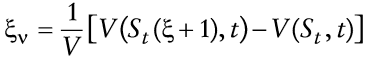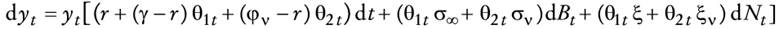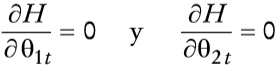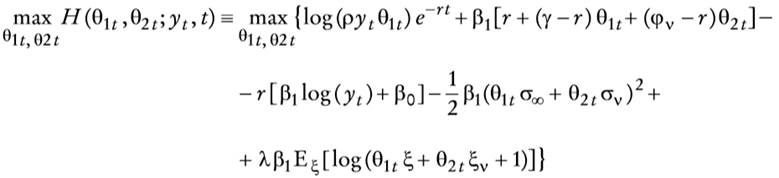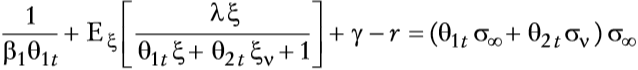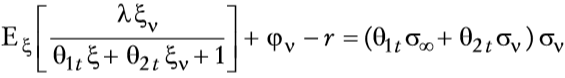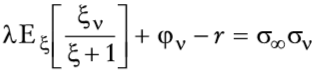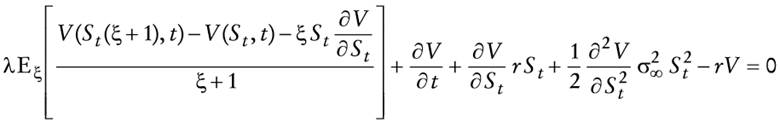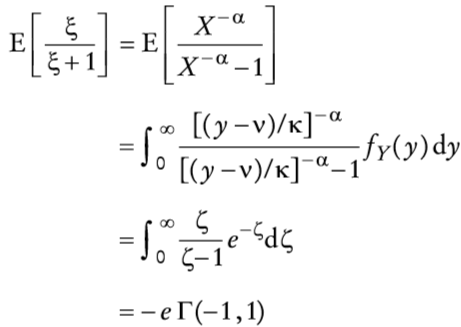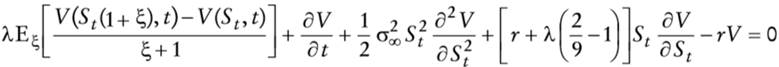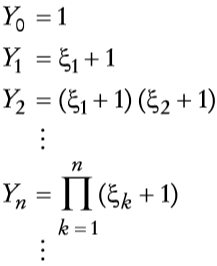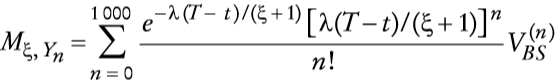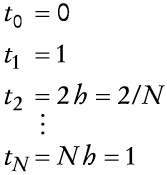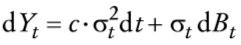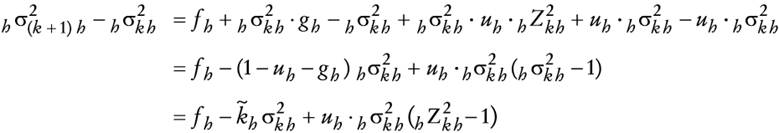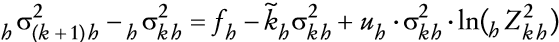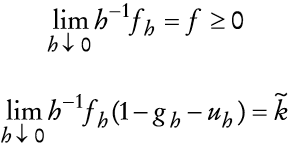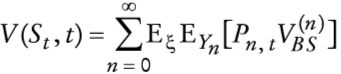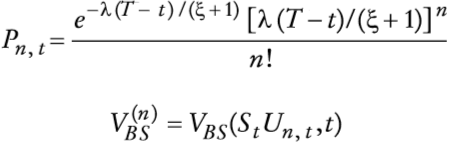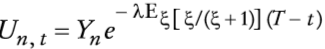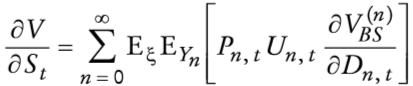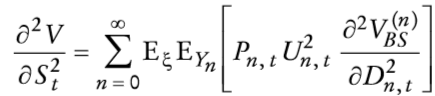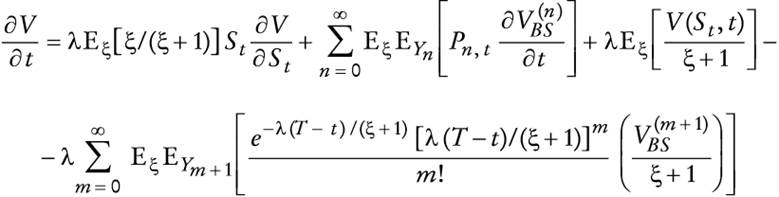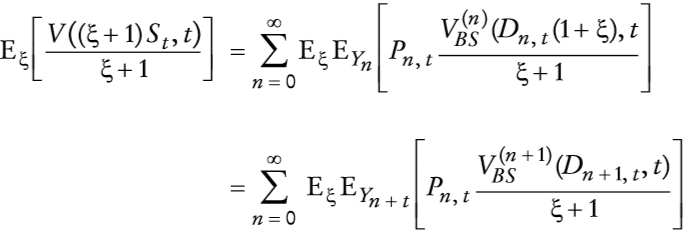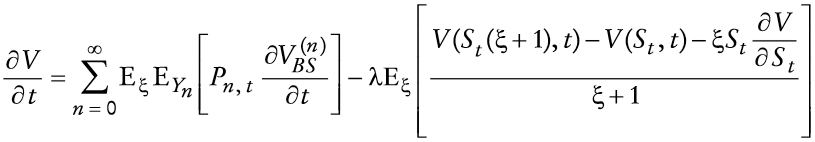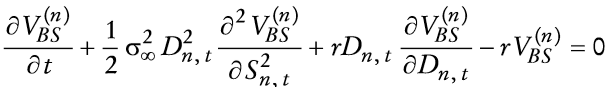Introducción

De acuerdo con el Fondo Monetario Internacional (FMI), actualmente, más de 20% de los países en el mundo tienen regímenes cambiarios que utilizan al tipo de cambio como un ancla nominal. Esta proporción es similar a la que se obtuvo en 1990. Las experiencias de México en 1994 y de Argentina en 2001 invitan a resaltar la necesidad de que los planes de estabilización basados en el tipo de cambio tienen que ser creíbles. A fines de 1994 el público mexicano estaba escéptico acerca de las acciones del gobierno para defender una tasa fija de devaluación combinada con una banda ajustable, el resultado fue un déficit insostenible en la cuenta corriente de la balanza de pagos seguido de un repentino auge en el consumo y una devaluación extrema. Por otra parte, el caso del plan de convertibilidad del gobierno argentino inició en 1991 y se abandonó en diciembre de 2001. Una vez más, en 2000, el público argentino anticipó el final del plan de estabilización, lo cual condujo a un auge en el consumo seguido de una devaluación extrema. En conclusión, uno de los puntos importantes que las autoridades fiscal y monetaria y los encargados de elaborar la política económica deben tomar en cuenta cuando estructuran un plan antiinflacionario, basado en el tipo de cambio, es que en la mayoría de los casos el resultado final es un incremento considerable en el consumo y una devaluación extrema.

Algunas de las investigaciones en la bibliografía especializada en estabilización temporal que han considerado un marco estocástico son, por ejemplo, ^{Drazen y Helpman (1988)} que analizan la estabilización con un tipo de cambio estocástico, ^{Calvo y Drazen (1997)} que consideran la incertidumbre en la permanencia de reformas económicas y ^{Venegas-Martínez (2001)}, (^2006a), (^2006b) y (²⁰⁰⁸) que estudia la estabilización cuando el tipo de cambio es conducido por un proceso de Itô. Asimismo es importante destacar los trabajos de ^{Uribe (2002)} y ^{Uribe y Mendoza (2000)} en cuanto a la explicación de los órdenes de magnitud de los auges inesperados de consumo y la incorporación de la incertidumbre en el análisis de los planes de estabilización temporal. Mientras que todas estas investigaciones han proporcionado avances teóricos considerables, existen todavía un par de regularidades empíricas que requieren ser explicadas, como lo señalan ^{Helpman y Razin (1987)}, y ^{Kiguel y Liviatan (1992)}. En primer lugar, en la mayoría de los casos, los planes de estabilización inflacionaria resultan en devaluaciones extremas y este hecho no ha sido incorporado todavía en el análisis y modelado de dichos planes y, en segundo lugar, la mayoría de los modelos carecen de una explicación plausible de la falta de credibilidad, incluso si no hay cambio en los parámetros que determinan las expectativas de devaluación.

Las opciones reales han cobrado recientemente un gran interés en macroeconomia; véase, por ejemplo, ^{Strobel (2005)} y ^{Henderson y Hobson (2002)}. El principal objetivo asociado con opciones reales es como evaluar productos derivados de activos no negociables.¹ En esta investigación se evalúa la opción real de posponer consumo en vísperas de que un plan de estabilización sea abandonado. En este caso, el activo subyacente de la opción es el precio del dinero en términos de bienes, es decir, el poder adquisitivo de una unidad monetaria.² Es importante destacar que el presente artículo proporciona una fórmula analítica del valor de dicha opción.

Esta investigación desarrolla, según el supuesto de una economía abierta y pequeña, un modelo estocástico de estabilización con ancla nominal en el tipo de cambio, reconociendo el papel que desempeñan los movimientos extremos en la dinámica de las expectativas de devaluación. Se supone que las expectativas de devaluación siguen un movimiento browniano mezclado con un proceso de Poisson en el que el movimiento browniano conduce a la tasa de devaluación y el proceso de Poisson modela una posible devaluación. Además, el tamaño esperado de una posible devaluación se supone que tiene una distribución de valores extremos del tipo de Fréchet. Con base en este marco teórico y suponiendo un agente representativo con utilidad logarítmica se examina las dinámicas de equilibrio del consumo y la riqueza real cuan do un plan de estabilización es instrumentado y el tamaño de una posible devaluación es conducido por una distribución de Fré chet. También, se estudia los efectos en el consumo y bienestar económico por cambios permanentes en los parámetros que determinan las expectativas.

El modelo propuesto se desarrolla según los tres si guien tes su pues tos: i) el ingreso del gobierno por señoreaje (seignorage) (impuesto inflacionario) no es rembolsado a los agentes, ii) los agentes perciben una tasa de devalua ción estocástica y iii) no existe un mercado de derivados (futuros, opciones o estructurados) que cubran el riesgo de posibles devaluaciones. El modelo que se establece proporciona soluciones cerradas, lo que ha ce más fácil el entendimiento de diferentes aspectos en la estabilización temporal, sobre todo cuando el tamaño esperado de una posible devaluación alcanza un valor extremo.

Por último, se enumeran varias características distintivas del modelo: i) existe falta de credibilidad aun cuando los valores de los parámetros que determinan las expectativas de devaluación no son modificados; ii) trata con horizontes estocásticos de estabilización; iii) reproduce vía simulación Monte Carlo, con valores apropiados de los parámetros, los auges de consumo privado en los casos de México en 1990-1994yArgentina en 2001-2003, los cuales resultaron en una devaluación extrema, y iv) se evalúa la opción real de espera cuando el consumo puede ser pospuesto en vísperas de que concluya un programa de estabilización de precios.

Es importante destacar también que en el modelo propuesto el proceso de inflación planteado no he re da to das las propiedades estadísticas del proceso estocástico del tipo de cambio, sino que el proceso de inflación mantiene un componente de mayor persistencia que la tasa de devaluación, tal y como lo muestra la evidencia empírica. Por otra parte, en cuanto a la decisiones óptimas del agente representativo se analiza: i) una solución interna en el sentido de que la fracción de la riqueza destinada a saldos monetarios reales es positiva pero menor a 1 y, por tanto, lo mismo aplica a la fracción de la riqueza destinada a bonos reales (que son los dos únicos activos), y ii) una solución de esquina, ya que el rendimiento real de los bonos es constante y el rendimiento real de los saldos monetarios reales sigue un proceso con tendencia estocástica con saltos hacia arriba, lo cual puede alentar al individuo a mantener sólo saldos reales. Por último, se estudia un experimento en el que la tasa media esperada de inflación toma un valor mayor a partir de cierto tiempo futuro y permanece allí para siempre. Es importante destacar que dicho experimento considera las probabilidades de que dicha política monetaria ocurra.

Este documento está organizado como sigue. En la sección I se considera una economía que produce y consume un solo bien y que está sujeta a una restricción cash-in-advance, en la que los agentes tienen expectativas de devaluación conducidas por un proceso de difusión con saltos de Poisson, y el tamaño esperado de una posible devaluación tiene una distribución de valores extremos. En la sección II se resuelve el problema de decisión de un consumidor representativo, tomador de precios y adverso al riesgo. Asimismo, en la sección III se realiza varios experimentos de política económica con diversos ejercicios de estática comparativa. En la sección IV se examina el efecto en el bienestar por choques exógenos en los valores de los parámetros que determinan las características de la economía. En el transcurso de la sección V se estudia el comportamiento de la dinámica de la riqueza y el consumo, y se conduce varios experimentos de la política cambiaria. En la sección VI se efectúa simulaciones Monte Carlo en la respuesta del consumo a cambios permanentes en los valores de los parámetros relevantes del modelo, en el supuesto de que el tamaño esperado de una posible devaluación tiene una distribución de valores extremos del tipo de Fréchet. En la sección VII se evalúa la opción de posponer consumo en vísperas de que expire un programa de estabilización de precios. Por último se presenta un conjunto de conclusiones, limitaciones y sugerencias para posteriores investigaciones. Al final, tres apéndices contienen pormenores de varios resultados analíticos.

I. Estructura del modelo

Se considera una economía pequeña y abierta poblada por consumidores con dotaciones y gustos idénticos, quienes viven para siempre en un mundo en el que sólo hay un bien homogéneo de consumo, el cual es internacionalmente comerciable. Los agentes mantienen dos activos: saldos reales y un bono real, cotizado y negociado internacionalmente, que paga una tasa de interés constante y libre de riesgo de incumplimiento.

1. Paridad de poder de compra y dinámica del tipo de cambio

Se supone que el bien internacionalmente comerciable es libre de barreras y aranceles para su compra o venta. El nivel general de precios internos, Q_t, está determinado por la condición de paridad de poder de compra, que está dada por

1

en que Qt*es el precio en moneda extranjera del bien en el resto del mundo y ε_t es el tipo de cambio nominal. De ahora en adelante, se supone por simplificación, que

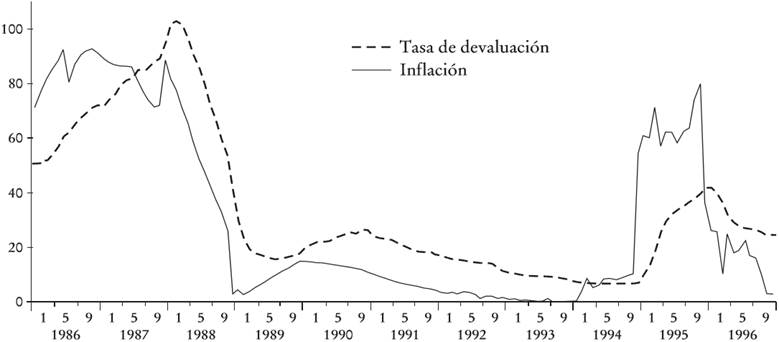
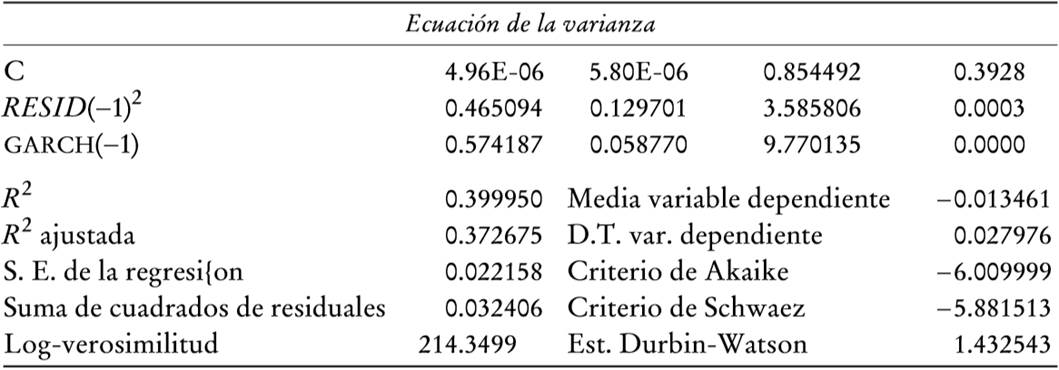
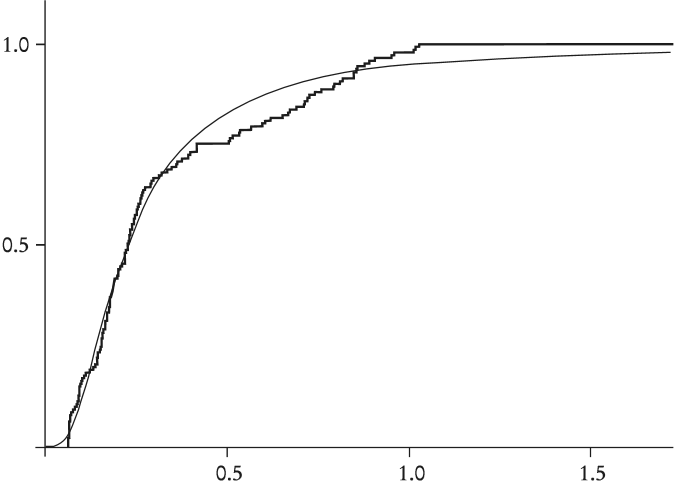
A continuación se modela la dinámica estocástica del nivel general de precios. Para ello se observa para el caso mexicano, en el periodo de análisis, que una característica sobresaliente de la inflación (el cambio porcentual del índice nacional de precios al consumidor, INPC) es que es considerablemente más persistente que la tasa de devaluación (ambas medidas como el cambio en el logaritmo a 12 meses) (véase el Apéndice 1). Con el propósito de modelar de manera adecuada la persistencia del proceso de inflación, se incorpora una versión continua de un proceso GARCH con media. En el Apéndice 1 también se muestra que el modelo GARCH(1,1)-M describe de manera adecuada la persistencia del INPC, de modo que:

y

en que π >0, Z_t ~ N(0,1) y f, g, u ≥ 0 en cuyo caso se puede demostrar (véase el Apéndice 2) que su versión continua satisface

y

en que k = 1 - g - u, y dB_t y dW_t tienen ambos distribución N(0, dt). Como se observa el proceso que conduce a la varianza, σt2, presenta reversión a un valor medio, σ∞2= f/k. Además, la solución de la ecuación diferencial estocástica de la varianza está dada por:

En este caso, la distribución estacionaria de a2 es la distribución γ inversa con parámetros v = 1 + 2k/u² y s = 2 f/u², es decir, 1/σt2 ~ Γ( ν, s).

Falta incorporar en el modelo los hechos estilizados de devaluaciones extremas. Para ello, de acuerdo con el análisis de estadístico de distribuciones de valores extremos realizado en el Apéndice 1, en la ecuación de tendencia es conveniente añadir un proceso de Poisson, dN_t, con un tamaño de salto aleatorio, Z, conducido por una distribución del tipo de Fréchet, esto es,

2

3

en que (B_t)_{t ≥ 0} es un movimiento browniano (o proceso de Wiener) definido en un espacio fijo de probabilidad con su filtración aumentada (Ω, FB,(FtB)_{t ≥ 0}, ℙ). De igual manera, el espacio de probabilidad en el que se define dW_t es (Ω, FW, (FtW)_{t ≥ 0}, P). Aquí FtB y FtW representan información relevante disponible al momento t. Asimismo, se supone que dNt es un proceso de Poisson con parámetro de intensidad. El tamaño de un salto hacia arriba es tal que

y

en que Y es una variable aleatoria de tipo de Fréchet con parámetros α, ν y κ> 0. Claramente, Z > 0. Nótese que un incremento en Y conduce a un aumento en X, el cual, a su vez, incrementa el valor de Z. En este caso se pude verificar que la función de distribución acumulada de Y está dada por

y la función de densidad de Y satisface

4

Obsérvese que si α > 2, entonces

y

Así que

Por otra parte, ya que el número de devaluaciones esperadas (es decir, saltos hacia arriba en el tipo de cambio) por unidad de tiempo sigue un proceso de Poisson dNt con intensidad λ se tiene que

y

así que

en que o (dt)/dt 0 cuando d t 0.Obsérvese que el tiempo esperado hasta el próximo salto es 1 /λ. Por último, es fácil mostrar que

2. Activos disponibles en la economía

El consumidor representativo mantiene dos activos reales: saldos reales, m_t M_t /Q_t, en que M_t es el acervo nominal de dinero y un bono internacional real de precio b_t. El bono paga una tasa de interés real constante r (es decir, paga un rendimiento de r unidades del bien de consumo por unidad de tiempo). De esta manera, la riqueza real del consumidor, y_t, está dada por

5

en la que y₀ es determinado exógenamente.

3. Financiación del consumo

La economía está equipada con una restricción cash-in-advance:

6

en la que c_t es consumo y ρ^-1 > 0 es el tiempo que el dinero debe ser mantenido para financiar el consumo. La condición (6) es fundamental para vincular la dinámica del tipo de cambio con el consumo. Adviértase que

en la que sigue se supondrá que el término del error o (l/p) es despreciable, en cuyo caso m_t = c_tρ. Es decir,

4. Rendimiento de saldos reales

La tasa de rendimiento estocástica por mantener saldos reales, dR_m, es sencillamente el cambio porcentual en el valor del dinero en términos de bienes. Al aplicar el lema de Itô al inverso del nivel de precios (es decir, al poder adquisitivo de una unidad monetaria), con (2) como la ecuación que conduce el proceso subyacente con volatilidad media σ_∞ y un valor de α despreciable, ya que la evidencia empírica, en el Apéndice 1, muestra un valor | α |<<1, en cuyo caso se tiene

El signo menos que aparece en el término -X-α es debido a que saltos en el tipo de cambio afectan de manera negativa los saldos reales. En conclusión, la tasa de rendimiento estocástica por la tenencia de saldos reales está dada por

8

II. Problema de decisición del consumidor

El cambio marginal de la riqueza real del consumidor en términos de la composición de la cartera θ_t = m_t /y_t y 1 - θ_t = b_t/y_t, así como del consumo, c_t, está dada por

con y₀ exógenamente determinada. La ecuación anterior puede ser reescrita, al sustituir (8) en la expresión anterior, como

9

en la que

La función de utilidad esperada del tipo Von Neumann-Morgenstern al momento t, I(y_t, t), de un consumidor representativo, competitivo y adverso al riesgo, con riqueza y_t, se supone que es de la forma:

10

en la que F_t = FtB⊗ FtWrepresenta toda la información disponible al momento t. Por simplificación, se supone que la tasa subjetiva de descuento del agente coincide casualmente con la tasa de interés internacional real, r, la cual se supone constante y libre de riesgo de incumplimiento. Este supuesto simplifica la dinámica estocástica del consumo. Se ha considerado la función de utilidad logarítmica con el propósito de obtener soluciones simples que hagan el análisis subsiguiente más sencillo.

1. Condiciones deprimer orden para una solución interna

La ecuación de Hamilton-Jacobi-Bellman del problema de control óptimo estocástico (o programación dinámica estocástica en tiempo continuo) de maximización de utilidad con log(c_t) = log(ρy_tt), según el supuesto de que es estocásticamente independiente de dN_t, está dada por

11

La condición de primer orden es

Dado el descuento de tipo exponencial en (10), se postula I( y t, t) de manera separable como

12

en la que G(y_t) = β₀ + β₁log(y_t) y g(t) = e^-rt. En este caso, las constantes β₀ y β₁ se determinan a partir de (11). Así pues, la condición (11) conduce a

13

en que

14

Adviértase que el argumento en la función logarítmica en (14) permanece positivo. Con el objetivo de calcular la condición de primer orden es necesario encontrar

A partir del resultado anterior se puede concluir que θ_t óptima es invariante en el tiempo, esto es, θ_t =θ, y satisface

15

Si se considera el siguiente cambio de variable

la esperanza matemática en (15) puede ser reescrita como

16

en que

Se debe tener presente para el análisis subsiguiente la siguiente fórmula para

17

en la que Γ(·,·) es la función γ incompleta. Se puede mostrar quer Γ(0,0) = ∞, Γ(0,∞) = 0 y Γ(0,1) = e^-1 o (1) ≈2/9. Por tanto, si se utilizan (16) y (17), la con dición de primer orden puede ser escrita como

18

Si se supone que 0< θ< 1, entonces la aproximación Γ(0,1/θ) ≈θe^1/θ (1 - θ) es aceptable, y se puede escribir la condición de primer orden como

19

la cual representa una ecuación cuadrática en θ (con raíces reales). Una vez que un óptimo θ es escogido, los coeficientes β₀ y β₁ son determinados a partir de (11), en cuyo caso:

20

lo cual conduce a

21

Así, la condición de primer orden produce

la cual es una ecuación cuadrática con raíces reales y sólo una raíz positiva dada por

22

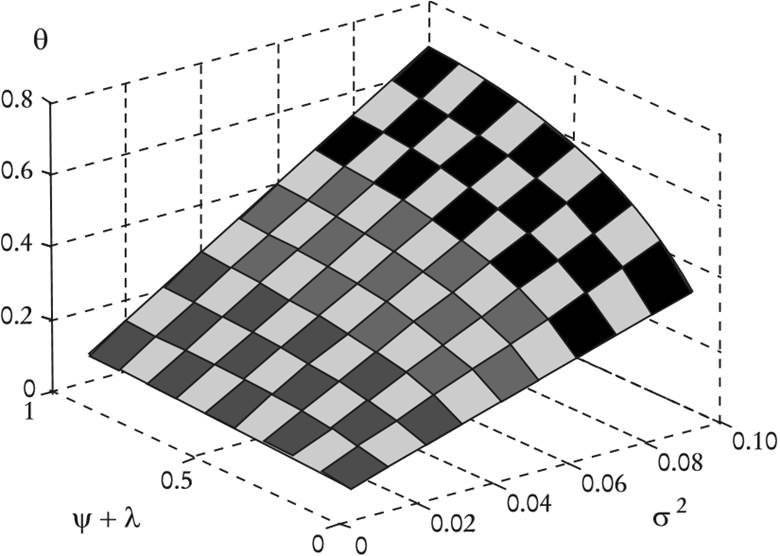
La Gráfica 1 muestra el valor óptimo de θ en función de ψ+λ y σ∞2, con r = 0.0850.

Gráfica 1 El valor óptimo de θ en función de ψ + λ y σ∞2  

2. Análisis de soluciones de esquina

La solución del problema de optimación de un consumidor racional obtenida en la sección anterior, ecuación (22), conduce a una solución interna en el sentido de que la proporción de la riqueza que se asigna a la tenencia de saldos monetarios reales es positiva pero menor a 1 y, por tanto, lo mismo sucede para la proporción de la riqueza destinada a bonos reales (estos son los dos únicos activos). Sin embargo no hay nada en la economía propuesta que asegure que esto se pueda cumplir. Por lo contrario, dados los supuestos del modelo es muy probable que esto no se cumpla y que se llegue a una solución de esquina. Lo anterior se debe simplemente a que la tasa de rendimiento real de los bonos es constante, mientras que el rendimiento real de los saldos monetarios reales sigue un proceso con tendencia estocástica y además permite saltos grandes. Es fácil imaginar situaciones en esta economía en la que los agentes mantengan sólo saldos reales y no bonos, debido a que el rendimiento de los saldos reales puede alcanzar un mayor monto respecto a los bonos reales. En efecto, obsévese que el rendimiento de los bonos es r y que el rendimiento esperado de los saldos reales es -π+ σ∞2 +λ. Ahora bien, en virtud de la identidad ψ = ρ + r + π - σ∞2, se tiene que

siempre y cuando ψ > ρ + λ (basta pedir que el consumidor no esté ansioso por el consumo presente y que la probabilidad de un salto y la volatilidad media de largo plazo sean pequeñas). A pesar de esta desigualdad entre rendimientos el agente no puede sólo mantener bonos ya que hay una restricción cash-in-advance. Si se desea que el consumidor sólo mantenga saldos reales será necesario compensarlo no sólo con π sino con algo más, digamos π +ψ, de tal suerte

Situación que también es congruente con el resultado principal de la sección

cuando θ = 1.

III. Experimentos de estática comparativa

En esta sección se realiza algunos experimentos de estática comparativa en relación con la decisión óptima θ. Se analiza el efecto en la θ óptima, 0 < θ < 1, por cambios en la tasa media esperada de la inflación π, la volatilidad instantánea de la inflación y el parámetro de intensidad λ. Al diferenciar totalmente la condición de primer orden, se tiene

23

en que

Un primer resultado relevante es que un incremento en la tasa de devaluación, la cual conlleva a un incremento en el costo de oportunidad de compra de bienes, conduce a una disminución permanente en la proporción de la riqueza asignada a saldos monetarios para facilitar el consumo. Para considerar esto, es suficiente utilizar (23), lo cual conduce a

24

Nótese también que un incremento en la varianza del componente de difusión producirá un efecto contrario al de π en θ debido a que

25

Dicho de otra manera, el consumidor asigna una mayor proporción de su ri queza para mantener saldos reales a fin de financiar consumo para enfrentar una mayor varianza en el precio del consumo.

Otro resultado importante es la respuesta de la proporción de la riqueza que se asigna en equilibrio a la tenencia de saldos reales, θ, por cambios en el parámetro de intensidad, λ. Un incremento en el número esperado de deva luaciones extremas por unidad de tiempo causa un aumento en el costo de oportunidad de comprar bienes. Esto, a su vez, disminuye permanentemente la riqueza asignada a saldos monetarios para facilitar el consumo. Además, a partir de (11), se tiene

26

Evidentemente, los cambios marginales (24), (25) y (26) están relacionados mediante

IV. Efecto en el bienestar económico

Ahora se evalúan los efectos de choques exógenos en el bienestar económico. Como es usual, el criterio de bienestar económico, Ω, del agente representativo es la utilidad máxima con riqueza real, y₀, es decir, la utilidad indirecta que proporciona la riqueza y₀. Así, el bienestar está dado por la expresión:

27

Con objeto de calcular el bienestar económico Ω, se necesita encontrar explícitamente, L(θ).Para ello, se usa el mismo cambio de variable que en(16), así

28

Es importante señalar que (16) puede ser obtenido al derivar (28), en efecto,

Adviértase que, debido a que se presenta una derivada en L(θ) en la condición de primer orden, se puede usar ahora la aproximación Γ(0,1/θ) _θe-1/θ(1 + O (θ)), de esta manera

Así pues, los efectos en el bienestar económico por cambios en la tasa promedio de devaluación, la volatilidad y la probabilidad de devaluación son, respectivamente:

V. Dinámica de la riqueza y en el consumo

Ahora se considera el proceso estocástico que genera la ri que za real del individuo cuando el óptimo θ es aplicado. Si se sustituye el punto óptimo θ en (9), se obtiene

29

La solución de la ecuación diferencial estocástica anterior, con condición inicial y₀, es

30

en que

31

Nótese que

32

En virtud de (6), el proceso estocástico para el consumo, en (30), puede ser escrito como

33

Esto indica que, en la ausencia de un mercado de productos derivados, el riesgo de devaluación tiene un efecto en la riqueza vía la incertidumbre en δ_t, esto es, la incertidumbre cambia el conjunto de oportunidades que enfrenta el consumidor. Por otra parte, el riesgo de devaluación también afecta la cartera de inversión vía efectos en θ. Así, un cambio en las variables de política estará acompañado tanto por efectos de riqueza como de sustitución. No se puede determinar el monto del consumo en este marco estocástico. Sólo se puede calcular la probabilidad de que, en un cierto intervalo de tiempo dado, un cierto monto de consumo ocurra. Asimismo, adviértase que de la desigualdad de Jensen, se tiene que el consumo esperado satisface

34

1. Consumo inesperado

En esta subsección se analiza una política de la forma:

en la que T (fecha en que se abandona el plan de estabilización) es exógena-mente determinado y π₁ < π₂. Nótese que en el modelo estocástico existe falta de credibilidad, aun cuando los parámetros permanecen constantes debido a que los agentes siempre asignan alguna probabilidad al evento de devalua ción de la moneda nacional. A continuación se analiza la respuesta de con sumo debido a la política anterior. A partir de (33) se puede escribir

en que

tiende a q₁/q₂ cuando Δ 0 c.s. (casi seguramente). Así,

35

También, se puede observar que θ₂ / θ₁< 1, junto con (35), implica que (q₁/ q₂) cr> limΔ0 c_T+Δ c.s., lo que indica un salto en el consumo al momento T. Si π fuera constante para siempre, es decir, si πt = π₂ para toda t ≥ 0 y q₁ = q₂, entonces se tendría

36

Por otro lado, a partir de (36), el término h_t( Δ ; π₁, π₂, q₁, q₂) 1 cuando Δ 0 c.s. En consecuencia, el consumo sería continuo c.s. para toda t. Si el plan de estabilización es temporal, entonces (q₁/q₂) cT>llimΔ0 c_T+Δ c.s., lo que indica un salto en el consumo al momento T, como se mostró antes. En particular, si q₁< q₂, se tiene que cT> lim_Δ-0 c_{T + Δ}; en caso contrario, aunque hay un salto, la desigualdad es ambigua y dependerá de las magnitudes de q₁ y q₂.

2. Horizontes de estabilización estocástica

Sea T una variable aleatoria distribuida exponencialmente con parámetro T--1. Supóngase que T es independiente de dB_t, dN_t y Y. Si se desprecia el término o(0 ) en(32)yse supone c₀ = y₀θ, entonces la tasa de crecimiento del consumo está dada por

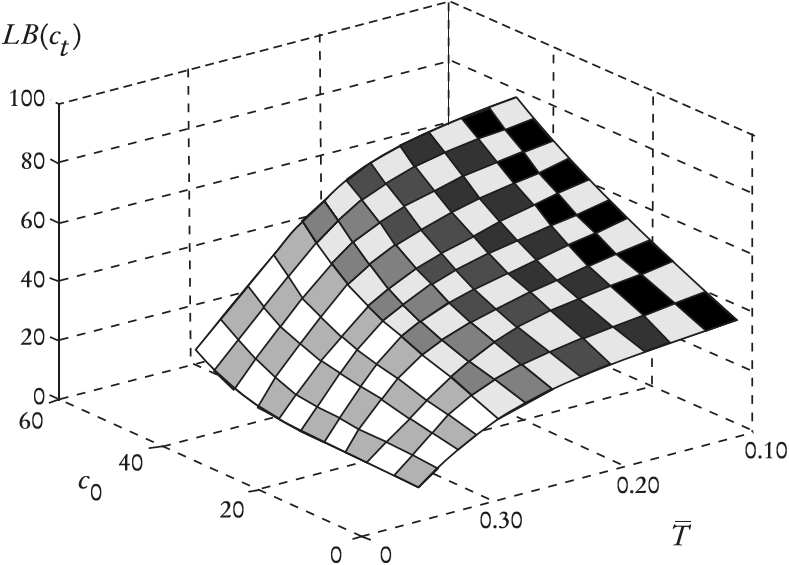
Si se aplica la desigualdad de Jensen en (34) el consumo tiene una cota inferior dada por LB(ct) = c₀ eE[δ_t]. La Gráfica 2 muestra a LB(ct) en función de c₀ y T-. Las unidades de c₀ están en términos de χ 10'' a pesos (mexicanos) de 1993. Se observa que cuando c₀ y T- aumentan, LB(ct) también aumenta.

Gráfica 2 LB (c_t ) en función de c₀ y T-[/p]  

VI. Ejercicio de simulación

El siguiente experimento consiste en intentar simular con el método Monte Carlo la respuesta del consumo a cambios en los valores de los parámetros que determinan las expectativas de la tasa de devaluación. El Cuadro 1 pre senta dos vectores con valores de los parámetros, (π_j,σj2,λj), j = 1, 2, que reproducen las tendencias del consumo observado en México entre 1989 y 1994.³ Se supone también que r = 0.0850 y y₀ = 1.849 χ 1012 (pesos de 1993). En este caso, se supone que κ = 1 y ν = 0.

Cuadro 1 Valores de los parámetros (caso mexicano) 

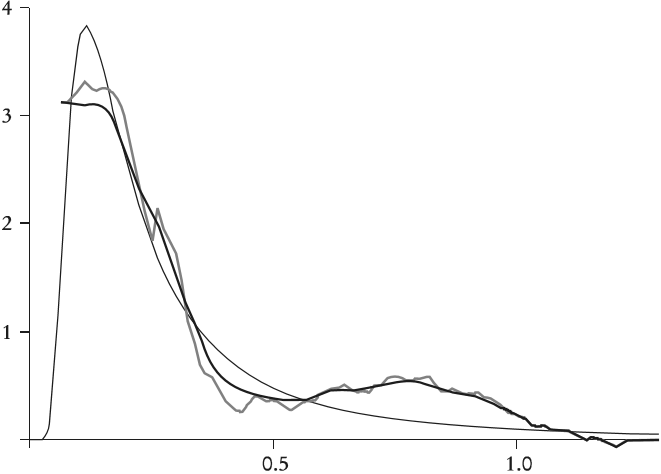
En la Gráfica 3(a) se han simulado trayectorias de: el movimiento browniano, el movimiento geométrico browniano y el proceso de difusión con saltos de Poisson y valores extremos.⁴ En la Gráfica 3(b) varias trayectorias simuladas son mostradas antes y después del primer trimestre de 1993. En la Gráfica 4(a) la línea punteada corresponde a consumo observado. En la Gráfica 4(b) la línea continua clara representa la tendencia simulada del consumo con el componente de difusión con saltos de Poisson. La Gráfica 4(c) muestra una línea continua ancha que representa la tendencia simulada del consumo con la componente de difusión con saltos de Poisson con un tamaño de salto conducido por la función de distribución del tipo de Fréchet. Finalmente, la Gráfica 4(d) compara la tendencia en 4 (b) y 4(c).⁵ Nótese que, con los valores de los parámetros, la simulación estocástica que considera una distribución de valores extremos imita el orden de magnitud del salto en el consumo observado en el primer trimestre de 1993; un salto de alrededor de 60 mil millones de pesos de 1993. El Cuadro 2 y la Gráfica 5 repiten el mismo ejercicio para el caso de Argentina 2001-2003.⁶

Gráfica 3 (a) simulación de trayectorias del movimiento browniano, movimiento geométrico browniano y procesos de difusión con saltos de Poisson y valores extremos; (b) simulación de varias trayectorias del consumo antes y después del primer trimestre de 1993  

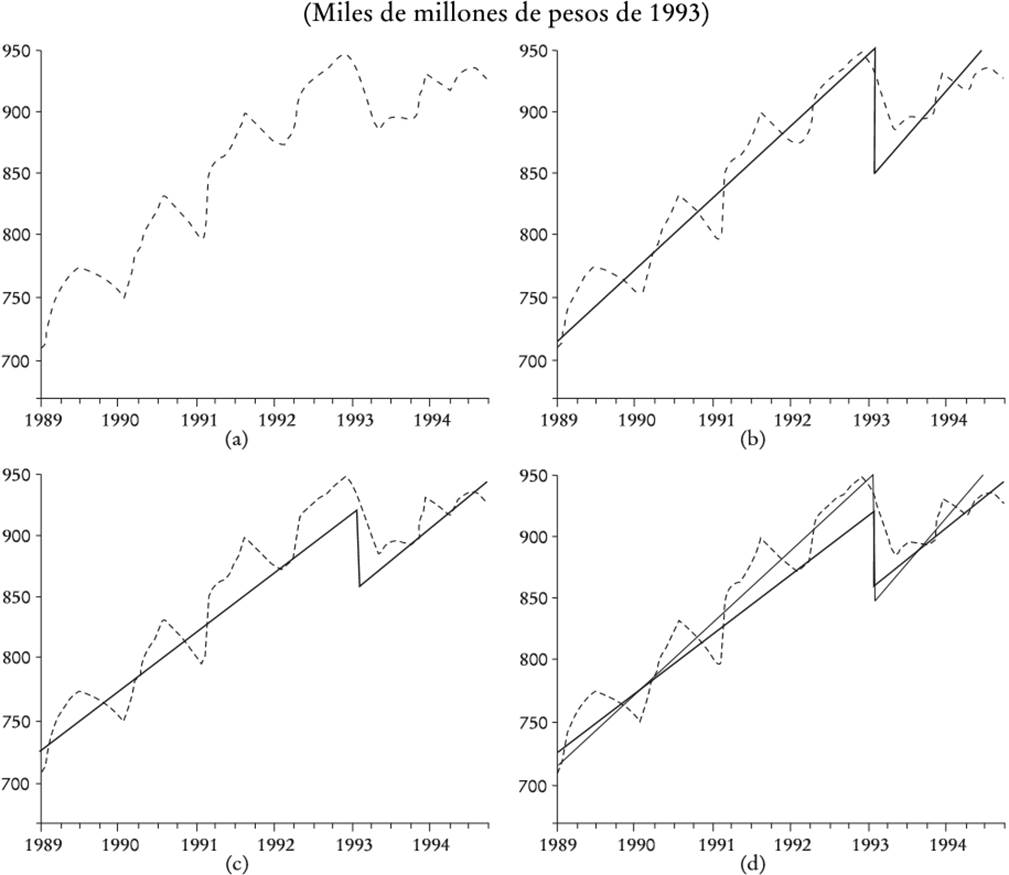
Gráfica 4 Simulación de tendencias del consumo: (a) consumo observado, (b) simulación de tendencia del consumo con la componente de difusión y saltos de Poisson, (c) simulación de la tendencia del consumo con la componente de difusión y saltos de Poisson y valores extremos, (d) se compara la tendencia en (b) y (c)  

Gráfica 5 (a) Simulación de trayectorias de consumo, (b) simulación de tendencias. La línea punteada corresponde al consumo observado en millones de pesos argentinos de 1993 

Cuadro 2 Valores de los parámetros (el caso argentino) 

VII. Opción real de posponer el consumo

En esta sección se caracteriza el precio de la opción real de posponer el consumo como la solución de una ecuación diferencial-integral. En primer lugar, obsérvese que la ecuación (7) puede ser reescrita como

37

en la que

Nótese que S_t = 1/Q_t es el precio del dinero en términos de bienes, es decir, el poder adquisitivo de una unidad monetaria; un activo no negociado. A partir de la definición de Z dada en (2), se tiene

Así, de (37), la tasa de rendimiento estocástica de los saldos reales, dR_m = dS_t/S_t, puede ser escrita como

38

Si V(S_t, t) denota el valor de la opción real de espera cuando el consumo se pospone y se utiliza el lema de Itô se tiene

39

O

en la que

y

En este caso, la restricción presupuestaria del consumidor, en términos de la cartera θ₁t = m_t /y_t, θ₂t = V_t /y_t, 1 - θ_1t - θ_2t = b_t /y_t, y consumo, c_t, está dada por

con y₀ exógenamente determinado. Es evidente que dRv = dV/V. Así, si se sustituye (38) y (39) en la expresión anterior, la restricción presupuestaria pue de ser reescrita como

40

en la que γ = σ∞2- π- ρ= φ - p. La ecuación de Hamilton-Jacobi-Bellman para el pro blema del control óptimo estocástico que maximiza la utilidad, con log(c_t) = log(ρ y ιθ₁₁), satisface

41

en que

Las condiciones de primer orden son:

Se postula I (y_t, t) de manera separable (multiplicativamente), es decir,

en que β₀ y β₁ con determinados de (41). Si se sustituye el candidato anterior en (41), se obtiene

Si se calcula ahora las condiciones de primer orden se encuentra que los valores óptimos de θ₁t y θ₂t satisfacen

y

Hasta ahora no se ha hecho algún supuesto de los valores de los parámetros. De ahora en adelante, sin pérdida de generalidad, se supone que γ =φ_{v- r}, esto es r = ρ. Si para evaluar la opción se supone una solución de esquina, θ_1t = 1 y θ_2t = 0, se tiene que

42

y

43

En este caso, se puede mostrar que β₁ = r^-1. Después de algunos cálculos simples, se tiene que las condiciones (42) y (43) conducen a

44

y

45

De (45) se sigue que

Si ahora se sustituye (44) en la ecuación anterior, se tiene

46

Se supone que las condiciones de frontera son de la forma V(0, t) = 0 y V(S_t, t) = max(S_t - K, 0), en la que K es el precio de ejercicio de la opción real (de posponer el consumo hasta el "último minuto" = T) .Obsérvese que el valor esperado anterior

en que f_ξ(·) es la función de densidad de ξ produce en (46) una ecuación di ferencial-integral. Obsérvese que si ξ es constante en (46), redefiniendo λ como λ /(ξ +1), se obtiene la fórmula de ^{Merton (1976)}. Por último, obsérvese que cuando ξ = 0 o λ = 0, la ecuación (46) se reduce a la ecuación diferencial parcial parabólica de segundo orden de ^{Black-Scholes (1973)}. Ahora bien, nótese que si se escribe

entonces

en que Γ (-1,1) = -Γ (0,1) + e-1. Se puede mostrar que Γ(0,1) ≈ 2/9 (de hecho, Γ(0,1) = 0.219383934...). De aquí que la ecuación (46) se pueda escribir como

Una posibilidad para de terminar V(S_t, t) consiste en definir una sucesión de variables aleatorias Yn con la distribución del producto de n variables alea torias independientes e idénticamente distribuidas ξ+1 con Y₀ = 1. Es decir, si {ξ_n}_n∈N es una sucesión de variables aleatorias independientes e idénticamente distribuidas, se define:

En este caso, la solución de la ecuación (46) con condiciones de frontera V(0, t) = 0 y V(S_t, t) = max(S_t - K,0), está dada por

47

en que ξ es independiente de {ξn}_n∈N y V_BS(·, ·)es la solución de Black-Scholes (véase el Apéndice 3).

Con el objetivo de obtener aproximaciones numéricas de (47), la cantidad dentro de la esperanza matemática en (47) dada por

es simulada usando el software estadístico Xtremes (^{Reiss y Thomas, 2001}) y la metodología de ^{Ripley (1987)} para las simulaciones Monte Carlo. Pos teriormente, se calcula el promedio de 10 mil valores simulados de M_t para obtener, con un valor particular de λ, una solución aproximada de la opción real de posponer el consumo. Para ello, en primer lugar se consideran los valores de los parámetros presentados en el Cuadro 3 para calcular el precio de referencia de Black-Scholes VBS(0).

Cuadro 3 Valores de los parámetros del precio de referencia de Black-Scholes 

En el Cuadro 3 la variable S_t representa el poder adquisitivo de una unidad monetaria, el parámetro K es el precio de ejercicio de posponer el consumo hasta el último minuto, r es la tasa de interés y T- t es el plazo. El Cuadro 4 muestra las aproximaciones numéricas del precio de la opción real al analizar simulaciones Monte Carlo para diferentes valores de λ con Eξ[ξ/(ξ +1)]=-eΓ(-1, 1). Se supone que, para propósitos de simulación, ξ sigue una distribución del tipo de Fréchet con media 0.01 y varianza 0.001. Las unidades de S_t y K están en pesos mexicanos de 1993.

Cuadro 4 Simulación del valor de la opción real 

Se puede concluir, del Cuadro 4, que el precio de la opción real de posponer el consumo aumenta cuando el número promedio de saltos de Poisson por unidad de tiempo se incrementa debido a un aumento en λ, lo cual au menta el costo de oportunidad para comprar bienes en el futuro.

Conclusiones

Se ha establecido un modelo estocástico de estabilización inflacionaria según el supuesto de que la credibilidad de sus alcances y duración es imperfecta. Las expectativas de los agentes fueron modeladas con un proceso de difusión con saltos para la tasa de devaluación, la cual presenta saltos provenientes de una distribución de valores extremos y un proceso de volatilidad estocástica con reversión a la media. Una característica importante de esta formulación es que existe falta de credibilidad aun cuan do los va lo res de los parámetros del proceso estocástico que conduce la tasa de devaluación per manecen constantes, ya que los agentes siempre asignan una probabilidad positiva el evento de devaluación. Al emplear una función de utilidad de tipo logarítmico se obtuvieron soluciones cerradas que permitieron analizar las repercusiones de una dinámica de devaluaciones extremas. Estas soluciones explícitas, aunque sencillas, también permitieron un análisis de importancia medular para explicar las consecuencias de los planes de estabilización que se espera que sean temporales.

Es importante destacar que el hecho de combinar un movimiento browniano con un proceso Poisson con el tamaño del salto conducido por una distribución de valor extremo aporta nuevos elementos para efectuar experimentos de simulación e investigación empírica de diversos hechos estilizados presentados en estabilizaciones temporales. Con este esquema, soluciones internas y de esquina fueron examinadas cuando es aplicado un plan de esta bilización con credibilidad imperfecta.

Se examinó también un experimento en el que la tasa media esperada de inflación toma un valor mayor a partir de cierto tiempo en el futuro y per manece allí para siempre, tomando en cuenta las probabilidades de que dicha política monetaria ocurra. Otro resultado importante que se obtuvo fue una expresión analítica para el precio de la opción real de posponer el consumo en vísperas de que el programa antiinflacionario sea abandonado. Y aunque los resultados obtenidos dependen, en gran medida, de la función de utilidad logarítmica, la cual es un caso límite de la familia de funciones de utilidad con coeficiente constante de aversión al riesgo, el precio de la opción real de posponer el consumo es independiente de las preferencias (por el consumo) del agente.

En la sección III en la que se realiza varios experimentos de política económica por medio de diversos ejercicios de estática comparativa, los resultados son muy intuitivos e interesantes. Es importante resaltar, ya sea en el supuesto de cash in advance o equivalentemente en el supuesto de transaction costs (como en ^{Uribe, 2002}), que los resultados dependen del comportamiento de los saldos reales, ya que al actuar la inflación como un impuesto (que distorsiona) al abandonar el programa desinflacionario se puede producir el efecto opuesto. La parte novedosa de los resultados encontrados es que la varianza de la inflación también puede ejercer un efecto que refuerza el efecto de la inflación media en el consumo si al disminuir la inflación también se reduce la varianza (inflation uncertainty); la bibliografía empírica del tema ha hecho gran hincapié en la correlación y/o causalidad de dichas variables.

Asimismo en la sección VI en la que se intenta simular por medio del método Monte Carlo la respuesta del consumo a cambios en los valores de los pa rámetros que determinan las expectativas de la tasa de devaluación, los resultados de la simulación son muy interesantes, pues se observa que la diná mica generada de inflación por dichas simulaciones está muy cercana a la observada.

Falta, por supuesto, extender el modelo para incluir bienes duraderos, lo cual proporcionará supuestos más realistas. Esta extensión dará lugar a dinámicas más complejas de analizar, pero los resultados serán todavía más acordes con lo que se observa en la realidad.