Introducción
En el artículo “Obtención y análisis de expresiones de cinética química. I. Obtención de datos cinéticos y criterios para evitar los problemas de transferencia de masa y energía utilizando catalizadores heterogéneos” (en este número) se abordaron las descripciones de rapidez de reacción, los tipos de reactores químicos y cómo evitar que datos obtenidos en el laboratorio estén afectados por la presencia de fenómenos de trasferencia de masa y energía. A partir de lo desarrollado con anterioridad, en este trabajo se parte de que tenemos datos experimentales idóneos (i.e. datos donde solo se está midiendo el efecto de la reacción química) y de ahí obtendremos los parámetros cinéticos confiables que proporcionen información del modelo cinético de reacciones catalíticas. En este artículo se describe el procedimiento en general para realizar el ajuste de los coeficientes cinéticos. Para alcanzar el ajuste, se utiliza la sumatoria de errores al cuadrado (SSE: sum of square errors) como la función objetivo de la minimización lineal o no. Esta manera de proceder se conoce como mínimos cuadrados y ha mostrado, desde los años en que se implementó, que es un estimador robusto, consistente y que muestra variaciones pequeñas. En situaciones en que se está ajustando una reacción química simple (la reacción puede describirse con una ecuación estequiométrica y una ecuación cinética), la minimización puede alcanzarse con relativa facilidad; pues la función objetivo es escalar y puede considerarse lineal. En esta situación estamos hablando de la regresión lineal; pero, es conveniente aclarar que esta NO es método de mínimos cuadrados; en realidad es el método más simple de los métodos de mínimos cuadrados. Con reacciones complejas (más de una ecuación estequiométrica y más de una ecuación cinética) el procedimiento de minimización se complica y se requieren métodos de minimización más robustos. Es relativamente fácil darse cuenta del aumento de la complejidad cuando consideramos que en lugar de ajustar un coeficiente cinético k (parámetro) se deben encontrar los valores óptimos para la minimización de varias ks y, entonces, en lugar de un parámetro ahora tendríamos un vector de parámetros (ks).
En este artículo se destaca la importancia de la sumatoria de errores al cuadrado (SEE), que representa las diferencias (errores) entre los datos experimentales con el modelo matemático a ajustar. La SSE se utiliza como función objetivo para alcanzar la minimización. Se habla brevemente de los métodos para la minimización más comunes empezando por la regresión lineal y los métodos para casos no lineales. Finalmente, se muestran algunas maneras en que la literatura científica presenta los resultados de los ajustes; la “bondad” del ajuste se refiere a que se obtuvieron resultados adecuados para la representación matemática de la actividad catalítica. Este artículo no pretende ser exhaustivo en la demostración de los métodos, más bien se enfoca en que un lector interesado tenga los elementos para elegir mejor cuál de los métodos de mínimos cuadrados se ajusta a sus necesidades.
Optimización (ajuste) de parámetros cinéticos
En general, el algoritmo que nos conduce al mejor ajuste, o a la obtención de parámetros cinéticos óptimos, se presenta en la Figura 1.
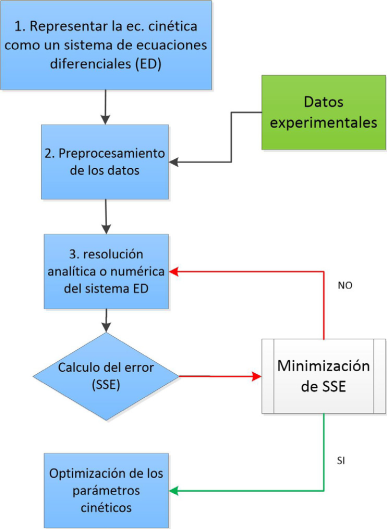
Fuente: Elaboración del autor.
Figura 1 Algoritmo general para optimizar los parámetros cinéticos utilizando mínimos cuadrados.
Para cumplir con la etapa 1, plantear el sistema de ecuaciones diferenciales (ED), se debe tener un cierto conocimiento químico, que a su vez incluye cierta experiencia en cuanto al posible comportamiento de la reacción. En los casos más sencillos se conoce la reacción, también la estequiometría y con ellas se propone una ecuación cinética muy simple. En casos más complejos se establece un esquema de reacción que se representa con sus posibles expresiones matemáticas. Si se conoce el mecanismo se describen matemáticamente todos los pasos.
Las etapas número dos y tres están íntimamente relacionadas. Con el preprocesamiento de los datos nos referimos a la manera en la cual se deben presentar los datos (generalmente a un programa matemático) y con ello facilitar los cálculos inherentes al paso 3. Esto puede incluir pasos como: simplificar la forma en que resultó la solución analítica de sistema ED o normalizar los datos, entre otros.
Etapa tres (integrador). Aquí la operación fundamental es resolver el sistema de ED. Hay ecuaciones muy simples que se pueden integrar fácilmente. Algunos sistemas de ecuaciones diferenciales ordinarias también tienen resoluciones analíticas y, en cambio, también existen sistemas más complejos que solo tienen resolución numérica. Algunos de los métodos numéricos más utilizados en este punto son del tipo Runge-Kutta.
El procedimiento que lleva al ajuste es la minimización de la SSE, líneas abajo se presenta cómo se genera esta suma y su importancia en el ajuste. El procedimiento para la minimización de la SSE puede ser muy simple si estamos ajustando una sola reaccion (porque la ecuación cinética asociada es muy simple) o complicada, por ejemplo, con un sistema de varias reacciones. Generalmente, el criterio de decisión es si ya se alcanzó un valor predeterminado en la SSE; si es así terminamos la optimización. En caso contrario se tienen que predecir unos nuevos parámetros, regresar a la resolución del sistema ED y comparar los valores de esta solución con los datos experimentales, y de nuevo evaluar la suma de errores. El error (E) por cada punto se define como:
¿Por qué es importante la suma de errores SSE? Tómese en cuenta la Figura 2. Con la optimización de parámetros lo que buscamos es, con una función (f) propuesta, responder la pregunta: ¿con cuáles parámetros f se acerca lo más posible a los datos experimentales? Al obtener esos parámetros tendríamos el ajuste. Inicialmente requerimos una buena suposición de los valores de los parámetros (coeficientes cinéticos en nuestro caso) que describen el esquema de reacción. Con esta suposición, se traza la función supuesta (f), véase la Figura (2a). Se calcula la distancia (E) entre la curva y los puntos experimentales (ecuación 2). El ajuste debe pasar a la menor distancia posible a los puntos. Esta distancia es la sumatoria de todos los errores Σ(E). Para trabajar solo con números positivos se usa el cuadrado de cada distancia. Se genera una nueva suposición (Figura 2b), si la nueva suposición se realiza en la dirección correcta Σ(E)2 debe disminuir. En la Figura 2, como puede observarse la suposición fue simplemente un menor valor del parámetro ordenada en el origen. Así, estamos trabajando con la sumatoria del cuadrado de los errores (SSE). A la suma de cuadrados de errores también se acostumbra llamarla suma de residuos. La connotación de residuo es, entonces, la diferencia entre los puntos generados por la función supuesta y los datos experimentales.
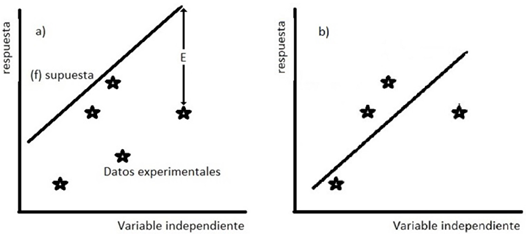
Fuente: Elaboración del autor.
Figura 2 Ajuste de parámetros: a) inicio del ajuste de parámetros con una suposición de parámetros inicial; b) con la metodología el ajuste mejora suposición.
Si bien algunos casos son simples y se ajusta un único valor de k, para algunos otros problemas debemos ajustar más de un parámetro, de esta manera se usa un conjunto de parámetros (vector kT = {k1, k2, k3, … , kn}). Entonces, f(supuesta) es una función de los parámetros a ajustar (coeficientes cinéticos) y la variable independiente (tiempo), es decir f(t, k). De tal modo, debemos buscar cuál valor para todas las k (parámetros en el modelo) da lugar a la menor SSE = Σ(E)2. Entonces, la suma de los cuadrados de los errores SSE(k) es la función objetivo que se minimiza.
argmin significa que realizamos una búsqueda de los parámetros (k) que convierten la sumatoria en un mínimo. Además, como se utilizan cuadrados, se acostumbra llamar a los métodos de búsqueda de los mejores parámetros métodos de mínimos cuadrados. La forma más simple de este tipo de métodos es el método de mínimos cuadrados lineal (regresión lineal) y también hay métodos para mínimos cuadrados no lineales.
Métodos de optimización de valores de los parámetros por mínimos cuadrados
Regresión lineal
El ajuste más simple de mínimos cuadrados se corresponde con una función lineal. Resulta que el procedimiento de optimización es tan simple que admite una solución analítica. El matemático francés Andréi-Marie Legendre fue el primero en publicarlo en 1805, aunque existen indicios de que antes trabajó en el tema el matemático alemán Carl Friedrich Gauss, quien lo planteó en 1794; pero, no lo publicó sino hasta 1809 (Mayorga y Osear 1988).
El método de regresión lineal se define como el procedimiento de análisis numérico en el que, dados un conjunto de datos experimentales de los que se sospecha siguen un comportamiento determinado por una función simple lineal con la variable independiente, se intenta determinar la recta (línea de mejor ajuste o línea de regresión) que mejor se aproxime a los datos experimentales. Dado que se tiene una gráfica, la representación sencilla proporciona una demostración visual de la relación entre los puntos (véase Figura 2).
El término lineal es porque la función supuesta se refiere a la ecuación de una línea recta:
Donde m es la pendiente y b la ordenada en el origen. Para este caso, el mejor estimado por mínimos cuadrados es:
para la pendiente, y:
para la ordenada en el origen, donde x es la variable independiente
y = datos experimentales o la respuesta
n = número de datos experimentales.
El ajuste se obtiene de manera directa realizando las operaciones de las ecuaciones (4) y (5). En contraste con lo anterior, cualquier ajuste no lineal es mucho más difícil de realizar. A continuación se hablará de los métodos para la minimización de una función no lineal. Téngase en mente que se sigue hablando de la minimización de los residuos.
Optimización de funciones multivariable no lineales por mínimos cuadrados
Con la finalidad de explicar cómo funcionan en general los métodos de optimización no lineal, empezaremos recordando el método de Newton utilizado métodos numéricos para obtener las raíces de una función.
Método de Newton
El método de Newton, también conocido como Newton-Raphson, fue implementado por Newton originalmente para obtener la raíz de un polinomio. Es conveniente aclarar que Newton veía su método como puramente algebraico y no hizo ningún intento de conectarlo al cálculo. A diferencia de la versión original del método, la versión moderna implementa las sucesiones y, por lo tanto, crea un algoritmo (Kerst 1946). En su versión más simple el método de Newton-Raphson es un algoritmo para encontrar las raíces (o ceros) de una función de una variable f(x) que es diferenciable. Esta función tiene su dominio en los valores reales (R). El método produce sucesivamente mejores aproximaciones a las raíces con la regla de sucesión:
La sucesión empieza con x0 como suposición inicial y debe localizarse razonablemente cerca de la raíz buscada. El método se basa en que se estima el valor de f(x) = y con la tangente de la función, es decir, su derivada f’(x), esto es, el nuevo valor predicho de, y sería:
Ahora necesitamos el valor de la nueva suposición xi + 1. Su valor se calcula de la intersección con el eje de las abscisas, esto es cuando y = 0
Finalmente, al despejar xi+1 se obtiene la fórmula de Newton-Raphson, ecuación (6). Cuando el valor de xi+1 se acerca a xi, dentro del criterio que se asignó para el error, se dice que se localizó la raíz y el método converge.
Aunque el método es confiable, pueden surgir diversos problemas, entre ellos:
El método falla en llegar a la convergencia, en ocasiones puede suceder que los valores sucesivos entren en un ciclo.
Depende demasiado de la suposición inicial, una mala suposición puede causar la no convergencia o un número de iteraciones excesivo.
El cálculo de la derivada puede ser difícil, incluyendo el que la derivada no exista en el punto asociado con la raíz.
Si la primera derivada no tiene un buen comportamiento y el método se dispara, es decir, el siguiente valor supuesto se aleja de la solución.
Existe la posibilidad de que el método alcance un punto estacionario y entonces los valores sucesivos ya no se mueven y no se cumple el criterio de convergencia.
Método de Newton multivariable
El método de Newton puede extenderse a variables múltiples, pero se debe considerar que en este caso cada variable tiene su raíz (cero) que atrae al punto de convergencia.
Método para k variables (o parámetros), k funciones
También se puede utilizar el método de Newton para resolver sistemas de k ecuaciones (no lineales), lo que equivale a encontrar los ceros de las funciones que deben ser diferenciables donde, también el vector de funciones está definido en los números reales: f (x1, x2, … xk): Rk → Rk. La ecuación en este caso es análoga a la del método de Newton para una variable (ecuación 8); tiene su equivalente en:
Donde Jf es la matriz del jacobiano de la función, esto es:
La comparación con el método de Newton original muestra que como resultado de trabajar con funciones multivariable se sustituye la multiplicación de 1/f’(x) por la inversa de la matriz jacobiana Jf-1(xi).
Al realizar las operaciones de cómputo se puede ahorrar tiempo cuando en lugar de resolver la inversa de la matriz jacobiana, se resuelve el sistema de ecuaciones lineales:
Quizá en este momento nos preguntamos: ¿y esto qué tiene que ver con la optimización? Pues regresemos a las clases de cálculo diferencial e integral. ¿Cómo se localiza un mínimo (o máximo)? Pues el criterio más simple es utilizar la primera derivada. En el mínimo (o máximo) la primera derivada tiene un valor de cero. Así que, en el contexto de la optimización de parámetros, la optimización se realiza con la búsqueda del conjunto de parámetros que acerquen el valor de la SSE a cero, es decir, la minimizan.
Algoritmo Gauss-Newton
El ajuste de funciones no lineales es complicado porque requiere encontrar matrices jacobianas y derivadas parciales (Glen, 2017). No obstante, existen algoritmos para realizarlo, por ejemplo, el algoritmo Gauss-Newton (GNA: por sus siglas en inglés Gauss-Newton algorithm) que es una modificación del método de Newton. El GNA es un algoritmo iterativo para resolver problemas no lineales de mínimos cuadrados. Iterativo significa que utiliza una sucesión de cálculos basados en conjeturas iniciales (x0) para calcular valores (xi) donde cada valor de xi se acerca a la solución. El GNA se utiliza generalmente para encontrar el modelo teórico de mejor ajuste, aunque también podría ser utilizado para localizar un solo punto. Dado que el algoritmo está basado en el método de Newton puede presentar los siguientes problemas:
Si la conjetura inicial no es buena, encontrar una solución es muy difícil -de encontrar (converger)- o puede que no se halle una en absoluto.
El procedimiento no es adecuado para matrices jacobianas que están mal condicionadas o deficientes en el rango.
Si los residuos relativos son muy grandes, el procedimiento perderá una gran cantidad de información.
En algunos casos, el GNA puede llevarse cientos de iteraciones el encontrar una solución (suponiendo que exista). Por lo tanto, se realiza casi exclusivamente con software. Los pasos básicos que realizará el software (tome en cuenta que los pasos siguientes son para una sola iteración):
Haga una suposición inicial x0 para xi
Haga una suposición para i = 1
Crear un vector f(xi) con las funciones f(xi)
Crear una matriz jacobiana para JF
Resolver (JF(xi)(xi+1 − xn) = − f(xn))
La siguiente suposición corresponde a la ecuación recursiva: xi+1 = xi + JF (xi )-1 F(xi ).
Repita los pasos 1 a 6 hasta la convergencia.
Método del gradiente (descendente)
Consideremos la siguiente situación: tenemos que subir en bicicleta una cuesta muy empinada. Esto es más fácil si se sigue un camino en zigzag, porque después de cada vuelta el ángulo de subida es menor al de la pendiente; pero la distancia recorrida es mayor. En contraste, si tuviéramos la fuerza de piernas, podríamos subir más rápidamente. En la situación contraria, si queremos llegar rápidamente a la parte más baja de la colina (equivalente a un valle o en matemáticas un mínimo), podemos tomar el camino recto (y quizá tendríamos problemas con el control). El algoritmo del gradiente descendente DGA (descent gradient algorithm), se obtiene con la traducción de este concepto a términos matemáticos. Para encontrar el mínimo de una función en un menor número de pasos debemos tomar la dirección contraria a donde se produce el cambio máximo. La derivada direccional de máximo cambio de una función es una de las definiciones de gradiente. Por lo tanto, la regla recursiva para realizar las iteraciones (equivalente a la ecuación 8) es:
Donde γ, pertenece a los números reales. El vector gradiente de una función (∇F(xi ) o grad(F(xi)) está definido por:
En la ecuación 12, si γ es lo suficientemente pequeña y como la dirección elegida es contraria a incrementos de f(xi); entonces se genera una secuencia monotónica descendente:
Y entonces esperamos que converja en un mínimo, que de preferencia debe ser global.
Algoritmo Levenberg-Marquardt
El algoritmo Levenberg-Marquardt (LMA, Levenberg-Marquardt algorithm). Realiza una interpolación entre los métodos Gauss-Newton y el gradiente descendente. Este algoritmo fue publicado en 1944 por Kenneth Levenberg y redescubierto por Donald Marquardt (Marquardt, 1963). Regresando al problema de la minimización por mínimos cuadrados planteado, más arriba, en la ecuación (2):
Para empezar la búsqueda del mínimo, debemos proponer un vector de estimaciones iniciales kT = (k1, …, ki). Para la búsqueda del mínimo global, las suposiciones de cada uno de los parámetros k (en las mediciones cinéticas, los coeficientes) deberían estar preferentemente cerca de la solución final.
En el algoritmo LMA, la regla de sucesión ocupa ligeras modificaciones del vector de parámetros k, que es remplazado por una nueva estimación k + 𝛅 en principio, el desplazamiento (𝛅) también puede ser un vector. Entonces, la nueva respuesta f(xi, ki + 𝛅i) se estima considerando una linealización de la función f(xi, k):
Donde Ji es de nuevo la matriz jacobiana; pero ahora, note que f es función de xi y del vector de parámetros ki.
En este momento, la nueva aproximación para la suma de residuos SSE(k) sería:
Tomando la derivada de SSE(k + 𝛅) con respecto de 𝛅, e igualando el resultado a cero, el sistema se resuelve con:
La contribución del método LMA es que se sustituye la ecuación anterior con:
Comparación del comportamiento de los diferentes métodos de minimización
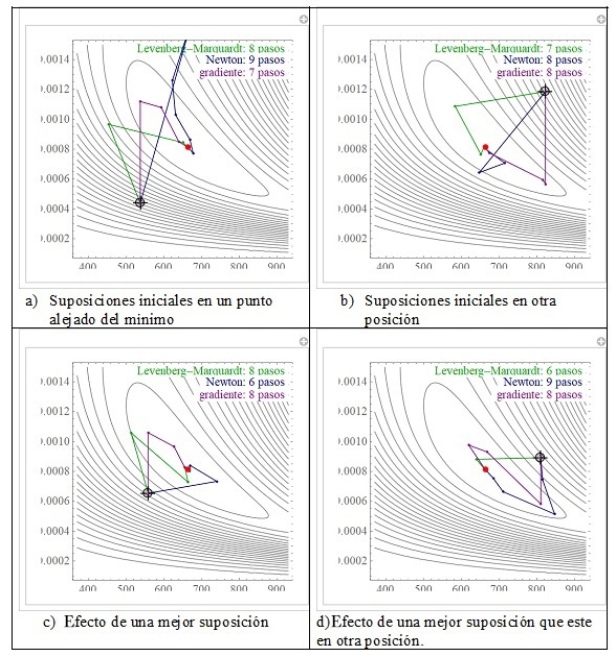
En la siguiente serie de gráficas es posible estudiar el comportamiento de los métodos de minimización. El ajuste que se está realizando es el crecimiento de levadura, modelado con la ecuación logística. El punto rojo es el mínimo de la función, que tiene la forma de un tazón. También se presentan las curvas de nivel. Las figuras se realizan en el software MATHEMATICA™ y son adaptadas de una demostración de Ruskeepää (Ruskeepää 2009).
En la Figura 3a, se observa claramente la forma de proceder del método Newton-Raphson, la primera iteración se proyecta fuera de la gráfica. Mientras que la segunda ya se acerca al mínimo; pero está del lado contrario de las suposiciones iniciales. Para el método del gradiente descendente note en las Figuras 3a y 3c que el camino para el mínimo es el mismo; porque es el que tiene el valor de máximo cambio. El algoritmo Levenberg-Marquardt es una combinación de los de Newton-Raphson y GNA y en la segunda iteración ya está muy cerca del mínimo. También se presenta el comportamiento si se trabaja con mejores suposiciones iniciales.
Ejemplo 1:
La condensación del formaldehído (F) con el parasulfonato de sodio (B) fue estudiada por Stults y McCarthy (1952) en un reactor intermitente. Los datos de la rapidez de formación del monómero (MA) se siguieron a 100 ºC y pH = 8.35. Inicialmente, las cantidades presentes de A y B eran iguales. Ajuste la expresión de ley de potencias.
Tabla 1 Datos obtenidos en laboratorio.
| CF, gmol/L | 0.131 | 0.123 | 0.121 | 0.117 | 0.111 | 0.104 |
| t, min | 0 | 10 | 20 | 30 | 40 | 60 |
Fuente: Elaboración del autor.
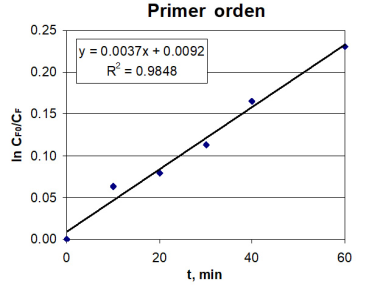
Empezaremos suponiendo una ley de potencia de primer orden; la ecuación es tan simple que la solución analítica es inmediata:
Separando variables e integrando:
Lo que nos pide la ecuación anterior es que el preprocesamiento de los datos es simplemente calcular -ln(CA/CA0), obtenemos:
Tabla 2 Datos a utilizar en el ajuste para un primer orden.
| t, min | 0 | 10 | 20 | 30 | 40 | 50 |
| CA0/CA | 1 | 1.0650 | 1.0826 | 1.1196 | 1.1801 | 1.2596 |
| ln CA0/CA | 0 | 0.0630 | 0.0794 | 0.1130 | 0.1657 | 0.2308 |
Fuente: Elaboración del autor.
La ecuación resultante es una línea recta kt = -ln(CA/CA0); así es que una regresión lineal simple es nuestro método de minimización y es suficiente. Esto se puede realizar con software, por ejemplo, Microsoft Excel™. El agregar una línea de tendencia nos da la pendiente k y el coeficiente de correlación. Es más recomendable trabajar con Excel™ regresión lineal en la sección análisis de datos. Los resultados se presentan en la Figura 4.
Criterios de confiabilidad estadística para el ajuste de una función
Una vez que la computadora arroja el resultado de un ajuste corresponde al investigador decidir qué tan bueno es el ajuste y aceptar o no los resultados. Para ello se apoya en criterios estadísticos para tomar la decisión. A continuación, se discutirán algunos de los criterios más comunes.
Coeficiente de correlación (R2)
El coeficiente de correlación se utiliza para determinar la “bondad” de un ajuste. Esto quiere decir qué tan cercanos son los valores del ajuste a los datos experimentales. El coeficiente de correlación siempre se encuentra en el intervalo 0 ≤ R2 ≤1. Algunos autores consideran que el ajuste es bueno si R2 ≥ 0.98, pero esto en realidad depende del número de datos experimentales.
Residuos
Recordando nuestra función para los mínimos cuadrados:
Los residuos o errores SE(k) son las diferencias entre los datos experimentales y el mejor ajuste obtenido. Esto se puede representar en la Figura 5.
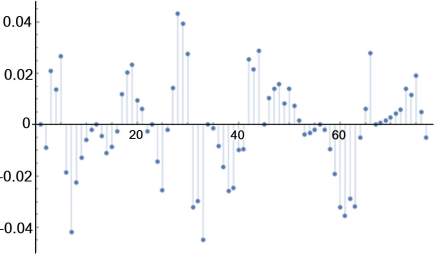
Fuente: Elaboración del autor.
Figura 5 Gráfica de residuos después del ajuste de un modelo cinético.
Los residuos deben distribuirse normalmente alrededor de la línea cero. Dicha línea representa el caso en que no hay diferencia entre el modelo ajustado y el valor predicho. También existe un menor error si los valores en el eje de las ordenadas, residuos, son lo más pequeños posibles. Nótese que con esta grafica se pueden identificar algunos de los puntos problemáticos, es decir, fuera del comportamiento normal; o, si hay un patrón en la distribución de los puntos, ambos casos significarían que se debe buscar un mejor ajuste.
Gráfica de paridad
La gráfica de paridad compara los datos experimentales contra los valores predichos del modelo ajustado. En estas gráficas se acostumbra representar la línea x = y como referencia; esta línea significa que los valores experimentales (x) son exactamente los predichos por el modelo (y). Lo ideal en esta representación es que en un buen modelo los puntos se localicen cerca de esa línea. Como ejemplo de este tipo de gráficas se tiene la Figura 11 (Alonso-Ramírez et al. 2019).
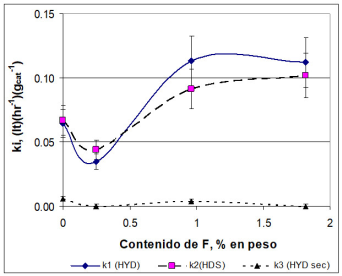
Nota: Se incluyen los intervalos de confianza.
Figura 6 Gráfica del ajuste de los coeficientes cinéticos de la reacción del dibenzotiofeno (DBT) para catalizadores NiMo/Al2O3.
Fuente: Nava Bravo et al. (2019).
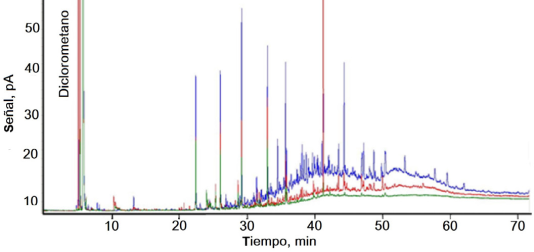
Figura 7 Cromatogramas de biocrudo obtenidos para tres condiciones de cosechado de microalgas.
Fuente: González-Gálvez et al. (2020).
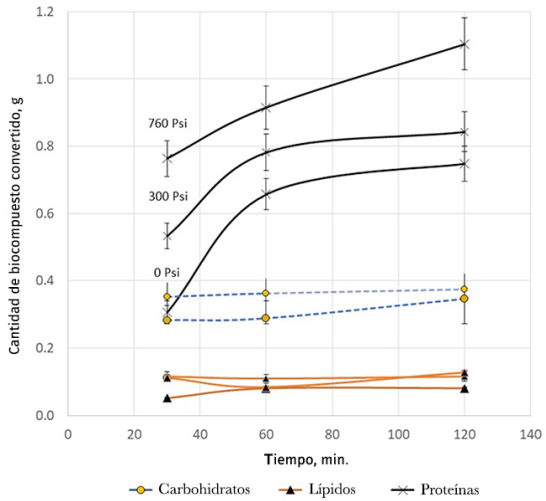
Figura 8 Conversiones por biomolécula en el proceso de solvólisis de un consorcio de microalgas rico en Spiruluna sp. En función de la temperatura.
Fuente: Alonso-Ramírez et al. (2019).
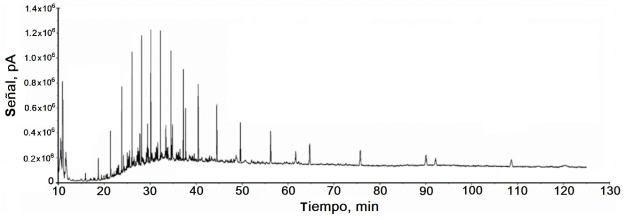
Figura 9 Cromatograma de la fracción de saturados de un crudo pesado.
Fuente: Alonso-Ramírez et al. (2019).
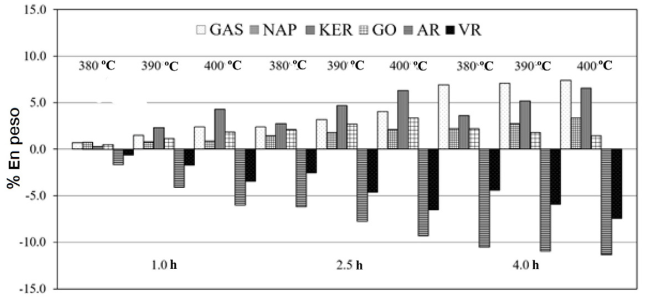
Figura 10 Rendimiento a diferentes fracciones después del proceso de mejoramiento de un crudo pesado en función de la temperatura y tiempo de reacción.
Fuente: Alonso-Ramírez et al. (2019).
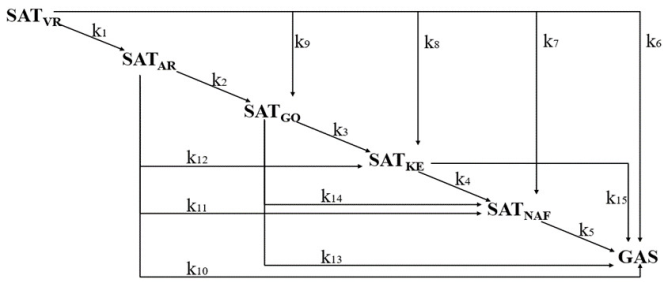
Figura 11 Esquema de reaccion de la fracción de saturados y sus efectos en los cortes de la destilación primaria.
Intervalo de confianza
El objetivo de esta gráfica es mostrar los límites donde al menos cae un porcentaje de los datos con los parámetros ajustados. Así, un límite de 95% significa que se tiene un 95% de probabilidad de que el valor “verdadero” del parámetro esté en ese intervalo. En otras palabras, si se realizaran experimentos independientes, para cada experimento y a partir de los datos obtenidos y sus respectivos ajustes, el valor del parámetro estaría en ese intervalo del 95% de las experiencias. En general, cuanto más cerca estén los límites de confianza del 95% del valor del parámetro, mejor será el ajuste. Como ejemplo se presenta la Figura 6.
Aquí se introduce otra situación para mejorar los resultados y la confianza que podemos tener en nuestros resultados; se está hablando de la repetición de los experimentos. Existen técnicas estadísticas para calcular cuál es el mínimo número de experimentos necesarios para dar confianza a los resultados, estamos hablando del diseño (estadístico) de experimentos, tema fuera del objetivo este artículo.
Gráfica de perturbaciones
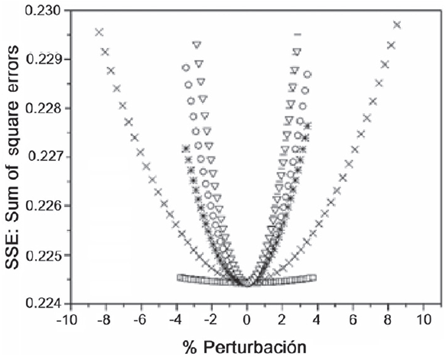
Ya se señaló que cuando estamos realizando un ajuste de una ecuación con varios parámetros, cada parámetro presenta su propio ajuste, y durante el ajuste cada una de las k estimadas tienden a su mínimo. Entonces, ¿cómo se distingue si nos encontramos en el mínimo global? Para ello se realiza la gráfica de perturbaciones. Con el ajuste obtenido se elige cualquiera de los parámetros (coeficientes cinéticos) y se le agrega (o resta) una cierta cantidad, creando, con ello, una perturbación en el modelo. Se calculan los valores de las otras k y se grafican los resultados. Estamos en un mínimo global si las perturbaciones en todas las k coinciden al mismo mínimo independientemente de la perturbación creada. Un ejemplo de este tipo de graficas se presenta en la Figura 13.
Fuente: Alonso-Ramírez et al. (2019).
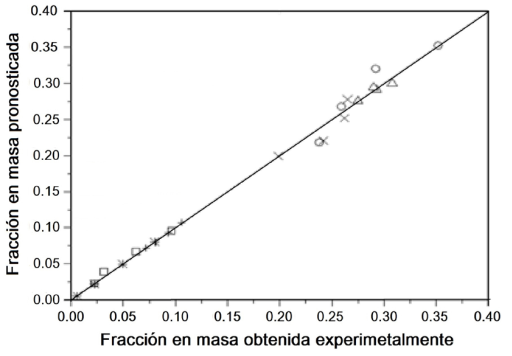
Figura 12 Curva de paridad para un modelo cinético propuesto por Alonso-Ramírez et al. (2019).
Como se ajustan hasta 15 coeficientes cinéticos, el trabajo no termina ahí, pues se debe garantizar que se alcanza un mínimo global, lo cual se realiza con la gráfica de perturbaciones. (Figura 13)
Fuente: Alonso-Ramírez et al. (2019).
Figura 13 Gráfica de perturbaciones para los coeficientes cinéticos calculados en el modelo presentado por Alonso-Ramírez et al. (2019).
Medidas de actividad catalítica en las publicaciones
En esta sección revisaremos algunos ejemplos de cómo se ha reportado en la literatura la actividad catalítica. Se muestran dos ejemplos que tienen esquemas de reacción muy complejos y cómo se ha avanzado en esos campos. En general, para las medidas de conversión se reportan intervalos de confianza. Si se han desarrollado y aceptado esquemas de reacción se pueden ajustar coeficientes cinéticos y cuando se conoce más se obtiene información sobre cómo funciona el nanocatalizador.
Producción de biocrudo utilizando microalgas
Si se está analizando un sistema muy complejo, por ejemplo, en el caso de producción de biocrudo a partir de biomasa el número de productos es muy grande. Se procesan diferentes tipos de biocompuestos: proteínas, carbohidratos y lípidos. Los carbohidratos pueden ser simples (azúcares) o complejos (celulosa). Por su parte, los lípidos pueden ser: fosfídicos, polares, no polares, entre otros. Cada biocompuesto es susceptible de sufrir reacciones distintas, por lo cual se generan demasiados compuestos; se desconocen también las posibles rutas de reacción. En la Figura 7, se presenta un cromatograma típico del biocrudo obtenido con el proceso HTL (hydrothermal liquefaction),1 donde se observa el gran número de compuestos químicos formados y de ahí la complejidad de estos. Con los problemas descritos, solo se está en condiciones de reportar balances en masa y los rendimientos, también en masa. En la Figura 7 se presentan cromatogramas después de procesar un consorcio de microalgas. Y en la Figura 8 las conversiones por biocompuesto que pueden obtenerse (Gonzáles-Gálvez et al. 2020).
De cualquier manera, en este tema, por el momento, todo experimento debe repetirse y entonces habrá que advertir cómo se reportan intervalos de confianza para cada medición.
Mejoramiento de crudos pesados
El objetivo de estos procesos es lograr un mejor aprovechamiento del crudo, transformando gran parte de los cortes más pesados (asfaltenos, residuos de vacío y atmosféricos) a cortes más ligeros. Se consideran mucho más valiosos los llamados destilados intermedios, porque en estos cortes encontramos a los precursores del diesel, keroseno, turbosina y gasolina. No es recomendable “sobretratar” el crudo porque entonces se pierden destilados intermedios al producir demasiado gas. El problema en este tema es el número de componentes que se encuentran en el crudo. Como ilustración se presenta, en la Figura 9, un cromatograma de solo una fracción del crudo que es la fracción de saturados (compuestos donde predomina el comportamiento químico de las olefinas). La mezcla total de crudo incluye, además, las fracciones de aromáticos, resinas y asfaltenos. Destacan como los picos de mayor intensidad precisamente los saturados, empezando por el heptano (C7) cerca de los 10 min y llegando hasta C27.
Discutiremos algunas gráficas tomadas del trabajo de Alonso-Ramírez et al. (2019), en cuyos experimentos se estudia el efecto de la temperatura (380, 390 y 400 °C) y tiempo (1, 2.5 y 4 horas) sobre la posible distribución de productos después de la destilación primaria. Como se puede observar, la Figura 10 está construida con porcentaje en peso. En las refinerías, la destilación primaria genera cortes distribuidos en función de la temperatura de ebullición. Los principales son gases ligeros (GAS), nafta (NAP), keroseno (KER), gasóleo (GO), residuo atmosférico (AR) y residuo de vacío (VR). Cuando tratamos un crudo pesado y si el proceso funciona consumimos AR y VG y sus rendimientos son negativos. Si estuviéramos interesados en producir gasóleo (GO) o keroseno (KER), lo mejor sería trabajar a 400 °C por 2.5 horas. Pero para nafta (antecedente de la gasolina) sería preferible operar por 4h y 400 °C.
Pero las investigaciones están avanzando y es posible predecir de qué corte antecedente puede provenir el corte generado y así optimizar las condiciones de operación para obtener el mejor rendimiento. Pero, para ello, hay que proponer un esquema de reacción. Para llegar al esquema de reaccion optimizado se propusieron y analizaron hasta 50 esquemas distintos. El esquema optimizado se muestra en la Figura 11.
Los ajustes se consiguieron con el algoritmo Levenberg-Marquardt (LMA). Para analizar la confianza en los resultados, se crea la gráfica de paridad de los valores de fracción en masa experimentales versus los predichos con el modelo (Figura 12). Un modelo confiable es cuando los valores predichos corresponden con los experimentales. Lo que está señalado con la línea a 45° en la gráfica.
Como se ajustan hasta 15 coeficientes cinéticos, el trabajo no termina ahí, pues se debe garantizar que se alcanza un mínimo global, lo cual se realiza con la gráfica de perturbaciones.
Reacción de HDS del dibenzotiofeno
Ahora se hablará de un esquema bastante más desarrollado en el tema de los nanocatalizadores de hidrotratamiento (HDT). Los catalizadores de (HDT) se utilizan para eliminar heteroátomos de diferentes cortes de crudo, en particular el azufre. Así, gracias a estos catalizadores tenemos gasolinas y diesel con bajos contenidos de azufre y se evitan problemas de contaminación. Los catalizadores de HDT son sulfuros de Mo, NiMo o CoMo soportados en alúmina. En estos nanocatalizadores se ha identificado plenamente la fase activa; en general, se habla de dos tipos de sitios donde ocurren reacciones de hidrogenación o reacciones de desulfuración. Se han aplicado varias técnicas de caracterización para identificar y cuantificar los sitios activos. Esta información es importante para mejorar el diseño del catalizador y/u orientar la preparación para procesar de mejor manera los distintos cortes de crudo.
Ejemplo 2:
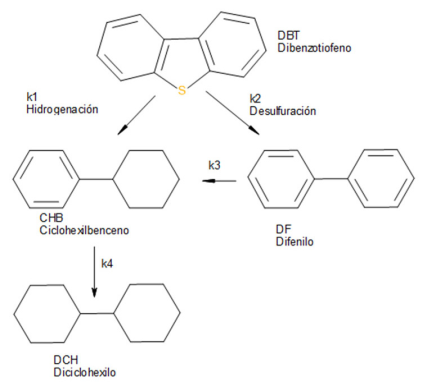
Analizaremos la reaccion de HDS del dibenzotiofeno (DBT). Y la utilizaremos para mostrar todo el proceso de ajuste usando Microsoft Excel™. Para esta reacción, se conoce el esquema de reacción, véase la Figura 14. Los tetra y hexahidro DBT son intermediarios de reacción, así que, generalmente, no los podemos detectar y se puede considerar que la reacción va del DBT al CHB y DF. En algunos nanocatalizadores se considera que la reacción del DF al CHB no existe. Y si el catalizador presenta una función hidrogenante fuerte se produce DCH
El proceso se realiza a presiones de hidrogeno altas; así, cada reacción se considera de pseudo primer orden. Del esquema construimos el sistema de ecuaciones diferenciales, en este caso ordinarias (EDO) (Cuevas-García, 2004):
Este sistema de ecuaciones diferenciales puede resolverse analíticamente (Cuevas-García 2004), para obtener:
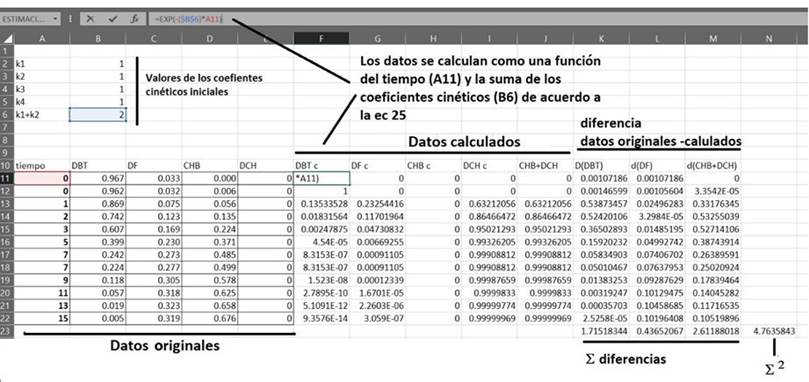
Nótese que, como resultado del procedimiento de solución en el preprocesamiento, los datos deben normalizarse como Ci/CDBT0 que, a su vez, es una definición de rendimiento. Como ejemplo se presenta, en la Figura 15, una captura de pantalla en Microsoft Excel™. Dado que fue posible resolver las ecuaciones analíticamente, se introducen las soluciones de cada ecuación (ecuaciones 24 a 28) en las celdas respectivas (celdas F11: J18). Por ejemplo, para el DBT calculado (DBTc), la variación de Ci/C0 en función del tiempo se muestra de las celdas F11: F18, y en cada celda se encuentra la ecuación 24. Se procede en forma similar con los otros compuestos. Como información adicional, en el ejemplo se evaluaban selectividades de hidrodesulfuración/hidrogenación y por eso se presenta una columna con la suma de los productos de hidrogenación CHB+DCH.
Fuente: Elaboración del autor.
Figura 15 Captura de pantalla de Microsoft Excel para el ajuste de los coeficientes cinéticos del esquema del DBT.
Los valores de los coeficientes cinéticos para el ajuste se presentan en las celdas B1: B6; en la captura de pantalla se muestra que la suposición inicial fue que todas las k = 1. Procedemos a realizar la minimización con la función solver de Microsoft Excel™. Se muestra en la Figura 16 otra captura de pantalla con los datos para usar solver. Se elige la celda N23 porque ahí se encuentra la SSE, como objetivo para la minimización; que se da a través de cambiar los valores de las k celdas B1: B6. Un buen método para la minimización en solver es el GRG (Generalized reduced gradient), versión basada en el método GDA.
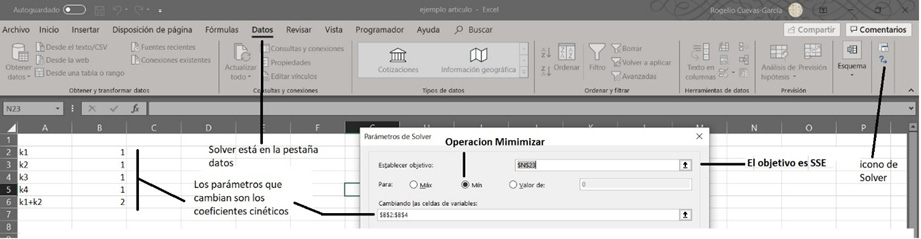
Fuente: Elaboración del autor.
Figura 16 Localización de solver en una hoja de Microsoft Excel™ y parámetros para la minimización.
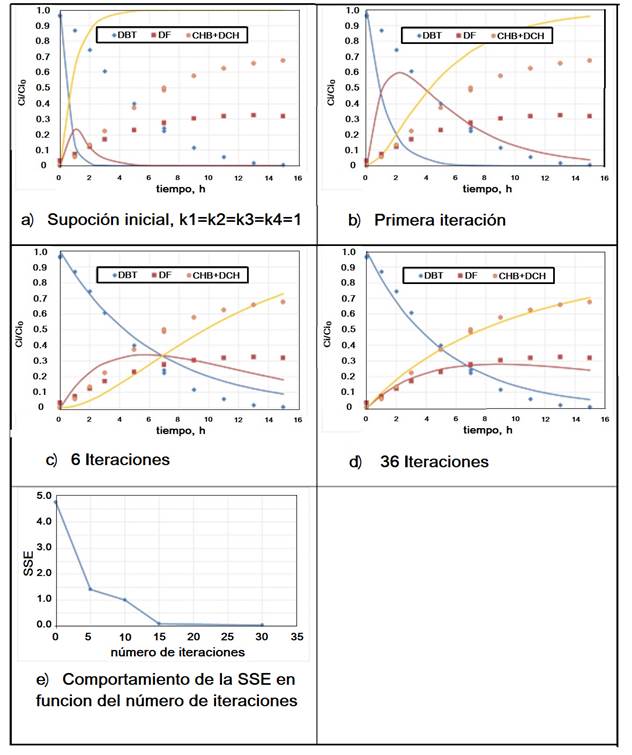
A continuación, se muestra cómo funciona el ajuste de los parámetros en Excel™; para ello, se presentan los resultados de ciertos pasos en la iteración que se va realizando, donde se busca la minimización de la SEE, como es usual, en el modelo se presenta como una línea recta y los puntos corresponden a las experiencias experimentales. En la Figura 17a se presentan las funciones considerando que los coeficientes cinéticos valen todos 1 (valores iniciales). Las Figuras 17b-17d muestran claramente que la minimización sigue un buen camino pues las distancias entre la función supuesta con los valores de k de la iteración están disminuyendo todas simultáneamente. En la Figura 17e, se muestra qué valores se van alcanzando con la reducción del SSE, para diferentes números de iteraciones. Finalmente, elegimos si se alcanza el criterio de convergencia SSE ≤ 1(10-4), la optimización termina. Por seguridad, también debe elegirse un número de iteraciones.
Recomendaciones
En este artículo se revisaron los métodos numéricos para realizar un ajuste para una ecuación cinética, y se describe la manera de realizar estos ajustes. Se presentó un ejemplo (esquema DBT) desde el punto de vista de cómo se realiza el ajuste. Aunque se trabaje con ecuaciones más complejas, básicamente, el procedimiento a implementar es el mismo; aunque la etapa de resolución debe de ser numérica. Si la complejidad del sistema es alta, se requiere el uso de software matemático más avanzado como MATHEMATICA™ y Matlab™. Este último tiene una nueva aplicación para ajustes cinéticos; pero, independientemente de la facilidad del uso del software, el conocimiento de cómo operan los métodos de mínimos cuadrados es fundamental para no caer en la equivocación de aceptar los resultados sin criterio.
Conclusiones
Por el momento el ajuste de las ecuaciones cinéticas tiene como fundamentos los métodos de mínimos cuadrados. La manera en que se crea un método de mínimos cuadrados es tener la suma de errores al cuadrado (SSE) como función objetivo y después se le aplica un método de minimización, lineal o no. La optimización consta de las etapas de representación de las ecuaciones cinéticas como un sistema de ecuaciones, obtención y preprocesamiento de los datos experimentales, resolución numérica o analítica del sistema de ecuaciones diferenciales resultantes y obedece en gran medida al método de minimización por mínimos cuadrados. Dependiendo del sistema de ecuaciones diferenciales a resolver cambia el método de minimización y entre los métodos se cuenta con regresión lineal, Newton-Raphson, Gauss-Newton, Gradiente descendente y Levenberg-Marquardt, entre otros. La decisión sobre la bondad del ajuste descansa sobre criterios estadísticos y existen varias formas de mostrar la confiabilidad de los resultados, entre ellas la presentación del coeficiente de correlación, la gráfica de residuos, representación del intervalo de confianza, la gráfica de paridad y las gráficas de perturbaciones.











 nueva página del texto (beta)
nueva página del texto (beta)