Introducción
La Ley de Benford describe el comportamiento que siguen los dígitos significativos (primera, segunda, tercera, ..., k-ésima posición en una cifra) de una secuencia determinada de números suficientemente grande, la cual establece que alrededor del 30% de tales dígitos empiezan con el número 1, aproximadamente el 18% con el número 2, y así sucesivamente hasta 5% que empiezan con el número 9 (la figura 1 ilustra esquemáticamente este hecho). La Ley de Benford también se conoce como Distribución Logarítmica.
Nota del Primer Autor. El primer contacto con esta interesante propiedad matemática fue hace algunos años, en una amena plática impartida en la Universidad de Costa Rica por el Dr. Theodore Preston Hill (Ted Hill), profesor investigador del Departamento de Matemáticas en el Instituto Tecnológico de Georgia, quien es uno de los principales precursores y contribuidor formal de la teoría y aplicación de esta ley matemática.
En particular, esta característica distintiva me pareció sumamente interesante y digna de ser compartida a un público general y fue el propio Ted Hill, quien (después de abordarlo al finalizar la plática y posteriormente contactarlo vía correo electrónico) al conocer mi interés de profundizar, aplicar y divulgar esta fascinante particularidad de los números, me animó a darle forma para publicarla en nuestro idioma con un lenguaje sencillo, para que no solo sea de dominio científico o académico, sino accesible a todo lector. Posteriormente, el tema atrajo la atención del segundo autor quien, junto con el estudiante de la Maestría en Ciencias de Datos y tercer autor, se sumaron y contribuyeron con la implementación de los algoritmos en lenguaje de programación Python para ejecutar los cálculos y verificar los resultados.
Un poco de historia
Esta regla matemática fue descubierta empíricamente hace poco más de 100 años y, de acuerdo a algunas investigaciones (citadas en [2, 3, 4, 9, 11]), a ésta se sujeta una impresionante variedad de secuencias de números obtenidas de fuentes reales de información cotidianas. Por ejemplo, listas de precios de supermercado, información numérica de extractos de periódicos y revistas, datos de censos y entrevistas, medidas en observaciones realizadas en laboratorios u originadas por procesos reales y sistemas dinámicos, series de tiempo, estadísticas deportivas y estudios de mercado, entre muchas otras más.
La Ley de Benford, después de muchos años de ser considerada solo como una curiosidad matemática, en la década de los noventa empezó a cobrar un serio interés por investigadores y usuarios de distintas áreas. En particular, cautivó nuestra atención y el objetivo es utilizarla como filtro primario en el análisis de datos de interés específico.
Una aplicación importante que ha tenido la Ley de Benford es principalmente en la detección de información fraudulenta. Hoy en día la utilidad de la Ley de Benford es equiparable al hecho que, en principio, el invento del teflón no fue ideado para aplicarse en los utensilios de cocina antiadherentes, pero se hizo y resultó de gran beneficio. Y lo mejor de todo es que no es necesario ser un erudito en la materia para utilizarla, casi en la misma proporción que es posible hablar del tiempo, sin saber cómo se construye un reloj o entender el funcionamiento del celular, sin necesariamente haberlo inventado o fabricado.
La primera observación sobre el comportamiento de los dígitos significativos fue una nota escrita (de dos páginas) por el astrónomo estadounidense Simon Newcomb [1], en la que hizo referencia a un “extraño capricho” encontrado en varios libros o tablas de logaritmos en algunas bibliotecas; los cuales en ese tiempo eran ampliamente utilizados por científicos y estudiantes para realizar sus cálculos. La observación de Newcomb fue que “las primeras páginas de tales documentos estaban más sucias que las restantes”, lo cual significa que el uso de las primeras páginas fue manifiestamente mayor que el de las últimas. Esto le permitió deducir que aparentemente los dígitos iniciales de los números que utilizaron de tales tablas no son equiprobables (como comúnmente se pensaría, con probabilidad de 1/9 o equivalentemente 11.11%), sino que el número 1 aparece como dígito inicial más frecuente, seguido del número 2, y así sucesivamente hasta el número 9 que es el de menor frecuencia de aparición como dígito inicial. La explicación obvia fue desconcertante: por alguna razón la gente hace más cálculos con números que empiezan con 1 que con 8 o 9. De hecho, a partir de un argumento heurístico, Newcomb proporcionó una fórmula simple que describe el patrón observado, la cual se expresa a continuación.
“Al parecer la naturaleza tiene predilección en ordenar los números de tal forma que la proporción de números que empiezan con el primer dígito D 1 es igual a
(aquí, allá y acullá)”.
Además, se tiene que la probabilidad de que un dígito dado esté en la segunda posición es
Mientras que para la tercera posición
donde
Por otra parte, para los primeros dos dígitos se tiene que
y, en general,
donde
También es posible trabajar con probabilidad condicional, entre otros conceptos relacionados.
En la tabla 1 se incluyen las probabilidades de ocurrencia para los primeros cuatro dígitos significativos, mismas que se obtuvieron al utilizar las fórmulas respectivas, verificando el resultado presentado en [2]. Además, enseguida se presentan ejemplos específicos.
Tabla 1 Probabilidad porcentual de los primeros cuatro dígitos significativos
| d | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Prob(D1=d) | 0 | 30.10 | 17.60 | 12.49 | 9.69 | 7.91 | 6.69 | 5.79 | 5.11 | 4.57 |
| Prob(D2=d) | 11.96 | 11.38 | 10.88 | 10.43 | 10.03 | 9.66 | 9.33 | 9.03 | 8.75 | 8.49 |
| Prob(D3=d) | 10.17 | 10.13 | 10.09 | 10.05 | 10.01 | 9.97 | 9.94 | 9.90 | 9.86 | 9.82 |
| Prob(D4=d) | 10.01 | 10.01 | 10.00 | 10.00 | 10.00 | 9.99 | 9.99 | 9.99 | 9.98 | 9.98 |
Ejemplos particulares de las operaciones anteriores:
a) Probabilidad de que un número tenga los tres primeros dígitos del número
b) Probabilidad (incondicional) de que el segundo dígito sea igual a 1
c) Probabilidad (condicional) de que el segundo dígito también sea igual a 1
Ley de Benford
No teniendo un argumento convincente, el artículo de Newcomb no fue de gran interés y el efecto de las páginas sucias de las tablas logarítmicas quedó en el olvido por más de medio siglo. Hasta que en 1938, Frank A. Benford [5], un físico que trabajaba para la Compañía General Electric en Estados Unidos, redescubrió tal efecto y se dio a la tarea de analizar grandes cantidades de datos obtenidos en distintos procesos: números que aparecían en periódicos y revistas, registros de drenado de presas en varios estados de la Unión Americana, áreas sembradas en terrenos agrícolas, información de censos de muchos condados, entre otros. Sin embargo, al igual que Newcomb, Benford tampoco tuvo una buena explicación del por qué se tenía el cumplimiento de esta singular ley de distribución de los dígitos para muchos fenómenos naturales.
¿Por qué Frank Benford mantuvo su interés centrado en este tema? Es algo que nadie sabe con certeza; es un hecho que se pierde en la historia. Sin embargo, su hobby consumía mucho tiempo (sobre todo en esa época en la que aún no existían computadoras ni calculadoras); dedicaba horas y horas a veces haciendo más de 20,000 cálculos enteramente a mano [2]. Su fascinación por la Matemática tenía poco que ver con la aplicación potencial que su pasatiempo pudiera llegar a tener, pero como alguien dijo por ahí: “las matemáticas son leales” (queriendo decir reales), y ¡sí que lo son! ¡Los números no mienten! La Matemática es leal y útil para analizar cualquier proceso real.
Finalmente, a partir de la última década del siglo XX, la Ley de Benford logró captar el interés de varios investigadores (de hecho, la base de datos Benford actualmente cuenta con más de 1,000 entradas de artículos, libros, software y videos) y se consolidó con el trabajo del Dr. Mark J. Nigrini [4], profesor de la West Virginia University, quien es conocido por sus contribuciones en auditoría y contabilidad para la detección de anomalías en los datos de empresas y del gobierno de los Estados Unidos (como la evasión de impuestos fiscales, alteración de nóminas, variación de precios de fábrica, aplicación errónea de pólizas de seguros, falsificación de patentes, malversación de cuentas gubernamentales, entre otras). Otro destacado investigador, quien demostró formalmente varios teoremas en relación con la Ley de Benford, es el Dr. Ted Hill [2], además de una larga lista de investigadores y aficionados que en los últimos años se han interesado y sumado en aplicar este principio en diversas áreas [6,11].
Características de la Ley de Benford
A continuación, se listan algunos hechos y propiedades que satisface la Ley de Benford, cuya justificación se encuentra en las referencias [2-4].
¡Los dígitos significativos son dependientes (y no independientes, como
pudiera esperarse)!
¡La Ley de Benford es invariante bajo escala, base y adición!
¡La Ley de Benford es sensible a la manipulación por redondeo!
¡La Distribución Benford es la distribución de distribuciones! (Teorema de Hill, 1996).
¡La distribución logarítmica particular (monótona decreciente), aunque no es universal, su alcance en la aplicación es sorprendente y en un primer vistazo se le encuentra en una amplia literatura: estadística, matemática, economía, ingeniería y de aficionados!
¡La Ley de Benford tiene muchas más caracterizaciones matemáticas!
¡Se invita al lector a investigar otras características interesantes!
Verificación de la Ley de Benford
En esta sección se analizan varios conjuntos de datos para verificar si cumplen o no la Ley de Benford. La variedad de ejemplos a seleccionar es amplia; sin embargo, debido al espacio e interés personal, el trabajo se enfoca en analizar la interrelación que tiene la Ley de Benford con la Teoría de Sistemas Dinámicos, muchos de los cuales se encuentran en la literatura, inclusive casos de sistemas caóticos, ver por ejemplo Tolle [6], cuyos resultados muestran la relación directa o indirecta que cumplen las coordenadas de las trayectorias en cuanto a la Ley de Benford. En particular, consideramos tres sistemas dinámicos clásicos para una elección adecuada de sus parámetros. Por otra parte, se verifica la Ley de Benford para la Sucesión de Fibonacci y se analiza una base de datos con altimetría de la Tierra, la cual contiene millones de valores.
1. Sistemas Dinámicos
Mapeo de Henón. El mapeo de Henón (figura 2a)) es un sistema de ecuaciones discreto con dos grados de libertad que genera estados que no cumplen la Distribución Benford para la elección predeterminada de algunos valores de los parámetros del sistema.
Se deja como ejercicio analizar el comportamiento del sistema en cuanto a Benford para otras elecciones de los valores de los parámetros y concluir al respecto.
Atractor “extraño” de Lorenz. El conocido atractor caótico de Lorenz, generado por el sistema 3-dimensional de ecuaciones diferenciales no lineales descritas en la figura 2b), para valores específicos de los parámetros involucrados satisface la Ley de Benford con diferente grado de error para cada una de las coordenadas. Se observa que aun cuando la solución para algunos valores de los parámetros no sigue de cerca la distribución Benford, la predominancia del número uno en la primera posición prevalece.
Sistema Rössler. El sistema continuo 3-dimensional (figura 2c), cuya gráfica se ilustra con escalas ajustadas), para la elección de ciertos valores específicos de los parámetros tiende a cumplir la distribución uniforme, mientras que para otros “simpatiza” con Benford.
Nota: La integración numérica para Henón, Lorenz y Rössler se realizó con un número considerable de iteraciones, diferente para cada caso, generando pares
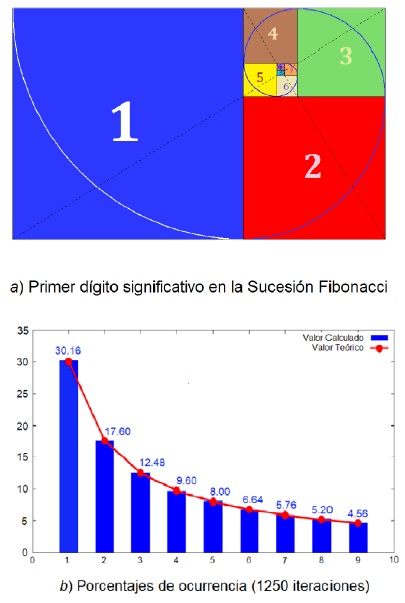
2. Prototipo en Matemáticas. Un ejercicio interesante es analizar la Sucesión de Fibonacci,
Esto es, a partir del tercer paso el término correspondiente se obtiene sumando los dos términos previos consecutivos.
Nota: Esta sucesión de números surge, por ejemplo, al considerar la cría de conejos en un medio confinado con recursos suficientes, entre otros procesos naturales. Por otro lado, la Sucesión de Fibonacci está estrechamente relacionada con la razón aurea o número de oro,
la cual está presente en muchas situaciones y aplicaciones reales, por ejemplo, en Geometría, Arquitectura, Ingeniería, Biología, Artes, entre otras.
Al realizar el cómputo, primero para
Observación: Un mayor número de iteraciones estabiliza la aproximación, pero el tamaño de las cifras de los valores generados se incrementa de forma considerable y se tornan difíciles de manipular. Por ejemplo, al aumentar las iteraciones a 1250 se tiene una mejor aproximación al resultado teórico (figura 3b)), pero las magnitudes de las últimas cifras son muy grandes.
Base de datos ETOPO1. Como aplicación específica se analizó una base de datos que contiene alrededor de 233,312,401 registros de las alturas sobre (+) y debajo (-) del nivel del mar en una malla que cubre la superficie del globo terráqueo. Esta es la base de datos ETOPO1, un modelo de relieve global de 1 minuto de arco de la superficie de la Tierra que integra la topografía terrestre y la batimetría oceánica, construido a partir de conjuntos de datos mundiales y regionales, la cual es de dominio público. Es importante observar que ya está disponible una actualización de esta base (resolución a 15 segundos de arco), para repetir el análisis y obtener conclusiones. Al realizar nuestro análisis, utilizamos la versión “Bedrock” de la base de datos ETOPO 1, la cual contiene la topografía terrestre y del fondo del océano sin considerar la capa de hielo de los polos, obtenida de la página oficial NOAA (National Oceanic and Atmospheric Administration)/ NCEI (National Centers for Environmental Information), https://www.ncei.noaa.gov/ (citada en [7]). Para realizar el presente ejercicio, se consideraron solo los valores positivos (elevaciones sobre el nivel del mar). La tendencia encontrada es que las elevaciones se concentran mayormente en aquellas en las que predomina el número 1 como primer dígito (1-2 m, 10-20 m, 100-200 m y principalmente 1000-2000 m), seguida de las que inician con 2, 3, 4, y así sucesivamente. En la figura 4 se ilustra la distribución de porcentaje de ocurrencia para cada número en la primera posición de las alturas registradas (base de datos Bedrock de ETOPO1).
Nota Importante. Los datos de la batimetría oceánica también fueron analizados y se observó que no cumplen la Ley de Benford, lo cual puede deberse a que hubo algún tipo de interferencia del mar sobre las lecturas de los dispositivos con los que se realizaron las medidas o se aplicó algún método de interpolación o ajuste para profundidades inaccesibles.
Conclusiones
Además de ser útil como herramienta auxiliar en el análisis y validación de datos obtenidos de sistemas dinámicos, ecuaciones diferenciales y en diferencias, teoría de matrices, métodos numéricos, series de tiempo y bases de datos de interés específico disponibles, hay otros trabajos relacionados con la Ley de Benford, tal como el descubrimiento de errores informáticos (computer bugs), detección de información errónea o fraudulenta [4, 9], aplicación en el diseño y diagnóstico de modelos matemáticos de interés específico [10], entre otros [7, 11].
Aun cuando la Ley de Benford no es una varita mágica para resolver cualquier problema, así como no lo es ninguna otra técnica o resultado matemático, esta puede llegar a ser de gran utilidad en el estudio de muchas situaciones importantes. Por lo tanto, vale la pena su estudio formal y aplicación o simplemente considerarla como pasatiempo, al igual como la tuvo en su momento Frank Benford, sumado a que actualmente se dispone de recursos de cómputo de vanguardia para un mejor y confiable análisis de bases de datos de distintas situaciones y procesos.











 text new page (beta)
text new page (beta)