1. Introducción
La subestructura o cimentación es aquella parte de la estructura que se coloca generalmente por debajo de la superficie del terreno y que transmite las cargas al suelo o roca subyacentes. Cada edificación demanda la necesidad de resolver un problema de cimentación. Las cimentaciones se clasifican en superficiales y profundas, las cuales presentan importantes diferencias en cuanto a su geometría, al comportamiento del suelo, a su funcionalidad estructural y a sus sistemas constructivos (Bowles, 1996; Nilson, 1999; Das et al., 2006).
Las cimentaciones superficiales, cuyos sistemas constructivos generalmente no presentan mayores dificultades pueden ser de varios tipos, según su función: zapata aislada, zapata combinada, zapata corrida o losa de cimentación (Bowles, 1996; Das et al., 2006).
El trabajo normal de análisis estructural se realiza normalmente con las hipótesis de que la estructura de los edificios está empotrada en el suelo, es decir, apoyada en un material indeformable (Calavera-Ruiz, 2000; Tomlinson, 2008).
La distribución de la presión del suelo bajo una zapata es una función del tipo de suelo, la rigidez relativa del suelo y la cimentación, y la profundidad de la cimentación a nivel de contacto entre la zapata y el suelo. Una zapata de concreto que descansa sobre suelos granulares gruesos (suelos arenosos) tendrá una distribución de presión similar a la Figura 1(a), cuando una zapata rígida está descansando sobre el suelo arenoso, la arena cerca de los bordes de la zapata tiende a desplazarse lateralmente cuando se carga la zapata, esto tiende a disminuir la presión del suelo cerca de los bordes, mientras que el suelo lejos de los bordes de la zapata está relativamente confinado. En contraste, la distribución de presión bajo una zapata que descansa sobre suelos finos (suelos arcillosos) es similar a la Figura 1(b), cuando la zapata es cargada, el suelo bajo la zapata desvía en una depresión en forma de cuenco, aliviando la presión bajo el centro de la zapata. Para fines de diseño, es común asumir que la presión del suelo se distribuye linealmente. La distribución de la presión será uniforme, si el centroide de la zapata coincide con la resultante de las cargas aplicadas, como se muestra en la Figura 1(c) (Bowles, 1996; Nilson, 1999).

Figura 1 Distribución de la presión bajo la zapata: (a) Zapata sobre suelos granulares gruesos; (b) Zapata sobre suelos finos; (c) Distribución uniforme equivalente.
Una zapata combinada es una zapata larga que soporta dos o más columnas en (típicamente dos) una fila (Kurian, 2005; Punmia et al., 2007; Varghese, 2009).
Las zapatas combinadas se utilizan cuando: 1) La relación existente entre cargas, capacidad admisible del suelo de la cimentación y la distancia entre columnas adyacentes imposibilitan la construcción de zapatas aisladas. 2) Una columna exterior queda tan cerca del lindero de la propiedad que no es posible centrar una zapata aislada bajo ella (Nilson, 1999; Kurian, 2005; Punmia et al., 2007; Varghese, 2009).
Las zapatas combinadas se diseñan de modo que el centroide del área de la zapata coincida con la resultante de las cargas de las dos columnas. Esto produce una presión de contacto uniforme sobre la totalidad del área y evita la tendencia a la inclinación de la zapata. Vistas en planta, estas zapatas son rectangulares, trapezoidales o en forma de T, y los detalles de su forma se acomodan para que coincidan su centroide y el de la resultante (Nilson, 1999; Kurian, 2005; Punmia et al., 2007; Varghese, 2009).
Otro recurso que se utiliza cuando una zapata sencilla no puede centrarse bajo una columna exterior, consiste en colocar la zapata para la columna exterior en forma excéntrica y conectarla con la zapata de la columna interior más cercana mediante una viga o una banda de amarre. Esta viga de amarre, al estar balanceada por la carga de la columna interior, resiste la tendencia a la inclinación de la zapata exterior excéntrica e iguala las presiones bajo ésta. Este tipo de cimentaciones se conoce como zapatas con vigas de amarre, en voladizo o conectadas (Nilson, 1999; Kurian, 2005; Punmia et al., 2007; Varghese, 2009).
Otra solución para diseñar las zapatas combinadas bajo columnas sometidas a flexión biaxial es considerar la presión máxima del suelo y esta es considerada uniforme en todos los puntos de contacto (Calavera-Ruiz, 2000; Tomlinson, 2008).
Algunos documentos recientemente publicados considerando la presión real del suelo son: Diseño de zapatas aisladas de forma rectangular utilizando un nuevo modelo (Luévanos-Rojas et al, 2013); Diseño de zapatas aisladas de forma circular utilizando un nuevo modelo (Luévanos-Rojas, 2014a); Diseño de zapatas combinadas de lindero de forma rectangular utilizando un nuevo modelo (Luévanos-Rojas, 2014b), esta zapata considera un solo lado restringido.
Este documento presenta un nuevo modelo para diseño de zapatas combinadas rectangulares de lindero con dos lados opuestos restringidos para obtener: 1) Los momentos alrededor de un eje longitudinal (un eje a-a con un ancho “b1”, y un eje b-b con un ancho “b2” que son paralelas al eje “Y-Y”; 2) Los momentos alrededor de un eje transversal (un eje c-c, un eje d-d, y un eje e-e que son paralelas al eje “X-X”); 3) La fuerza cortante unidireccional (Cortante por flexión) sobre los ejes f-f, g-g, h-h e i-i; 4) La fuerza cortante bidireccional (Cortante por penetración) sobre una sección rectangular formada por los puntos 5, 6, 7 y 8 para la columna 1 (frontera izquierda) y la sección rectangular formada por los puntos 9, 10, 11 y 12 para la columna 2 (frontera derecha). La presión real del suelo que actúa en la superficie de contacto de la zapata es diferente en las cuatro esquinas, esta presión se presenta en términos de los elementos mecánicos que actúan en cada columna (carga axial, momento alrededor del eje “X”, y momento alrededor del eje “Y”). El enfoque matemático sugerido en este trabajo produce resultados que tienen una exactitud tangible para todos los problemas, parte principal de esta investigación para encontrar la solución más económica.
2. Modelo propuesto
2.1 Consideraciones generales
Según los requisitos del Código de Construcción para Concreto Estructural y Comentarios, las secciones críticas son: 1) el momento máximo se encuentra en la cara de la columna, pedestal, o muro, para zapatas que soportan una columna de concreto, pedestal, o muro; 2) la fuerza cortante por flexión se presenta a una distancia “d” (distancia desde la fibra extrema comprimida al centro del acero de refuerzo longitudinal) se medirán desde la cara de la columna, pedestal, o muro para zapatas que soportan una columna, pedestal, o en la pared, y 3) la fuerza de corte por penetración se localiza de manera que el perímetro “bo” es un mínimo, pero no tiene por qué acercarse a menos de “d/2” a: (a) Los bordes o esquinas de las columnas, las cargas concentradas, o zonas de reacción, y (b) Los cambios en el espesor de la losa, tales como bordes de capiteles, ábacos, o tapas de corte (ACI, 2013; McCormac y Brown, 2013).
La ecuación general para cualquier tipo de zapata sujetas a flexión bidireccional es (González-Cuevas y Robles-Fernández-Villegas, 2005; Punmia et al., 2007; Gere y Goodo, 2009):
dónde:
σ: presión que ejerce el suelo sobre la zapata (presión del terreno),
A: área de contacto de la zapata,
P: carga axial aplicada en el centro de gravedad de la zapata,
Mx: momento alrededor del eje “X”,
My: momento alrededor del eje “Y”,
x: distancia en dirección “X” medida a partir del eje “Y” a la fibra en estudio,
y: distancia en dirección “Y” medida a partir del eje “X” a la fibra en estudio,
Iy: momento de inercia alrededor del eje “Y”,
Ix: momento de inercia alrededor del eje “X”.
2.2. Modelo para el dimensionamiento de las zapatas
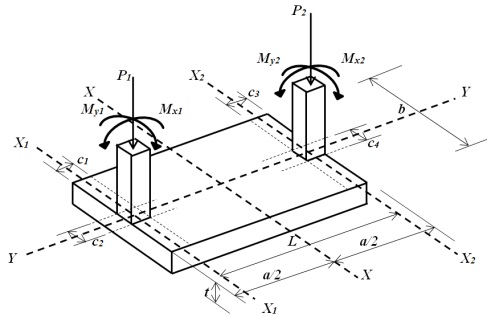
En la Figura 2 se muestra una zapata combinada rectangular de lindero con dos lados opuestos restringidos soportando dos columnas rectangulares de diferentes dimensiones, cada columna sujeta a una carga axial y momento en dos direcciones (flexión bidireccional).
El valor de “a” es fijo y se puede expresar en función de “L” como sigue:
dónde: a es la dimensión de la zapata paralela al eje “Y”.
Sustituyendo A = ab, Ix = ba3 /12, Iy = ab3 /12, y = a/2, x = b/2 en la ecuación (1) se obtiene:
dónde:
b: dimensión de la zapata paralela al eje “X”,
R = P1 +P2, MyT = My1 +My2: momento total alrededor del eje “Y”,
MxT = Mx1 +Mx2 + P1 (a/2-c1 /2)-P2 (a/2-c3 /2): momento total alrededor del eje “X”.
Si se considera que la presión del terreno debe ser cero, ya que el suelo no es capaz de resistir tracciones, el valor de “b” se obtiene:
Si se considera que la presión del terreno debe ser la capacidad de carga admisible disponible del suelo “σadm”, el valor de “b” se encuentra:
La capacidad de carga admisible disponible del suelo se obtiene de la siguiente manera:
dónde: qa es la capacidad de carga admisible del suelo, γppz es el peso propio de la zapata, γpps es el peso propio del relleno del suelo.
2.3. Nuevo modelo para diseño de zapatas
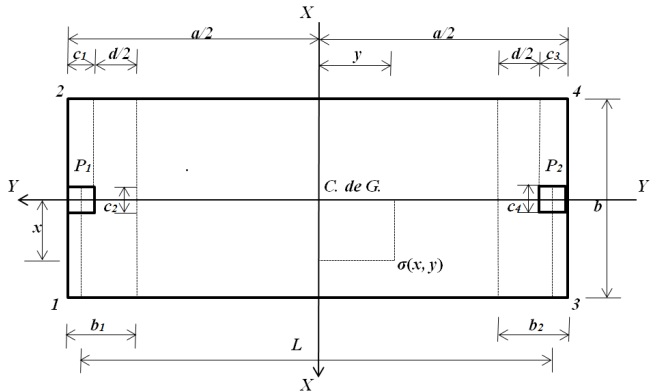
La Figura 3 muestra el diagrama de presión para zapatas combinadas rectangulares de lindero con dos lados opuestos restringidos sometidas a una carga axial y el momento en dos direcciones (flexión bidireccional) en cada columna, en donde la presión se presenta diferente en las cuatro esquinas y variando linealmente a lo largo de toda la superficie de contacto.

Figura 3 Diagrama de presión para zapata combinada rectangular de lindero con dos lados opuestos restringidos.
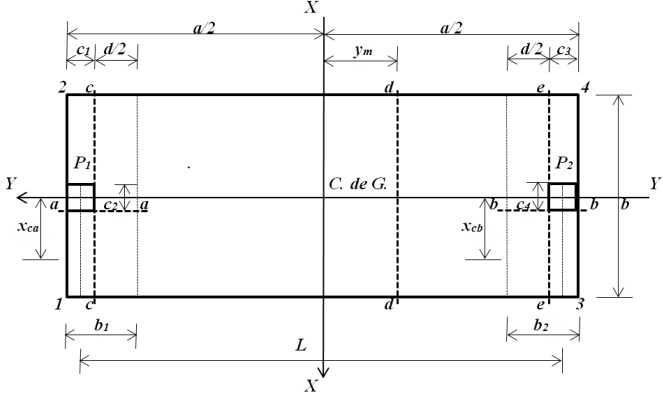
La Figura 4 presenta unas zapatas combinadas rectangulares de lindero con dos lados opuestos restringidos para obtener la presión en cualquier lugar de la superficie de contacto del miembro estructural debido a la presión que se ejerce por el suelo.
La presión del terreno en la dirección transversal es:
Para la columna 1 es:
Para la columna 2 es:
La presión del terreno en la dirección longitudinal es:
dónde: b1 = c1 +d/2 es el ancho de la superficie de falla bajo la columna 1, b2 = c3 +d/2 es el ancho de la superficie de falla bajo la columna 2.
2.3.1. Momentos
Las secciones críticas para los momentos se muestran en la Figura 5. Estas se presentan en las secciones a-a, b-b, c-c, d-d y e-e.
2.3.1.1. Momentos alrededor del eje “a-a”
La fuerza resultante “FRa ” se encuentra a través del volumen de presión de la zona formada por el eje a-a con un ancho b1 = c1 +d/2 y el extremo libre de la zapata rectangular, donde la presión mayor se presenta:
Ahora el centro de gravedad “x ca ” se obtiene:
El momento alrededor del eje “a-a” se encuentra por medio de la siguiente ecuación:
Sustituyendo la ecuación (10) y (11) en la ecuación (12) se obtiene:
2.3.1.2. Momentos alrededor del eje “b-b”
La fuerza resultante “FRb” se encuentra a través del volumen de presión de la zona formada por el eje b-b con un ancho b2 = c3 +d/2 y el extremo libre de la zapata rectangular, donde la presión mayor se presenta:
Ahora el centro de gravedad “xcb” se obtiene:
El momento alrededor del eje “b-b” se encuentra por medio de la siguiente ecuación:
Sustituyendo la ecuación (14) y (15) en la ecuación (16) se obtiene:
2.3.1.3. Momentos alrededor del eje “c-c”
La fuerza resultante “FRc” es el volumen de presión del área formada por el eje c-c y las esquinas 1 y 2, esta se presenta como sigue:
El centro de gravedad “ycc” del volumen de presión del área formada por el eje c-c y las esquinas 1 y 2 se obtiene:
El momento alrededor del eje “c-c” se encuentra por medio de la siguiente ecuación:
Sustituyendo la ecuación (18) y (19) en la ecuación (20) se obtiene:
2.3.1.4. Momentos alrededor del eje “d-d”
En primer lugar, se debe localizar la posición del eje d-d que es donde se ubica el momento máximo. Cuando la fuerza cortante tiene valor cero, el momento es máximo, entonces la fuerza cortante “Vy = FRd ̶ P1” a una distancia “ym” se presenta de la siguiente manera:
La fuerza cortante “Vy” se hace igual a cero y el valor de “ym” se obtiene:
El centro de gravedad “ycd” del volumen de presión del área formada por el eje d-d y las esquinas 1 y 2 se obtiene:
El momento alrededor del eje “d-d” se encuentra por medio de la siguiente ecuación:
Sustituyendo la ecuación (22) y (24) en la ecuación (25) se obtiene:
2.3.1.5. Momentos alrededor del eje “e-e”
La fuerza resultante “FRe” es el volumen de presión del área formada por el eje d-d y las esquinas 1 y 2, esta se presenta como sigue:
El centro de gravedad “yce” del volumen de presión del área formada por el eje e-e y las esquinas 1 y 2 se obtiene:
El momento alrededor del eje “e-e” se encuentra por medio de la siguiente ecuación:
Sustituyendo la ecuación (27) y (28) en la ecuación (29) se obtiene:
2.3.1.6. Ecuación de momentos entre las dos columnas
Para obtener la ecuación de momentos entre las dos columnas se sabe que la derivada del momento es la fuerza cortante, por lo tanto, se presenta como sigue:
dónde: My es el momento a una distancia “y”, Vy es la fuerza cortante a una distancia “y”.
La ecuación de la fuerza cortante es:
Sustituyendo la ecuación (32) en la ecuación (31) y desarrollando la integral se obtiene:
Ahora para evaluar la constante de integración “C” se sustituye y = a/2 ̶ c1 y Mc-c que aparece en la ecuación (21), el valor de la constante se muestra como sigue:
Sustituyendo la ecuación (34) en la ecuación (33), la ecuación de momentos se obtiene:
2.3.2. Fuerza cortante unidireccional (cortante por flexión)
La sección crítica para la fuerza cortante unidireccional se obtiene a una distancia “d” a partir del paño de la columna, según se muestra en la Figura 6, se presentan en la sección f-f, g-g, h-h e i-i.
2.3.2.1. Fuerza cortante en el eje “f-f”
La fuerza cortante por flexión “Vff-f” que actúa en el eje f-f de la zapata se encuentra por medio del volumen de presión del área formada por el eje f-f con un ancho “b1 = c1 + d/2” y el extremo libre de la zapata de forma rectangular, donde se presenta la presión mayor:
2.3.2.2. Fuerza cortante en el eje “g-g”
La fuerza cortante por flexión “Vfg-g” que actúa en el eje g-g de la zapata se encuentra por medio del volumen de presión del área formada por el eje g-g con un ancho “b2 = c3 + d/2” y el extremo libre de la zapata de forma rectangular, donde se presenta la presión mayor:
2.3.2.3. Fuerza cortante en el eje “h-h”
La fuerza cortante por flexión “Vfh-h” que actúa en el eje h-h de la zapata es la fuerza “P1” que actúa en la columna 1 menos el volumen de presión del área formada por el eje h-h y las esquinas 1 y 2 de la zapata y se presenta como sigue:
2.3.2.4. Fuerza cortante en el eje “i-i”
La fuerza cortante por flexión “Vfi-i” que actúa en el eje i-i de la zapata es la fuerza “P1” que actúa en la columna 1 menos el volumen de presión del área formada por el eje i-i y las esquinas 1 y 2 de la zapata y se presenta como sigue:
2.3.3. Fuerza cortante bidireccional (Cortante por penetración)
La sección critica para fuerza cortante bidireccional aparece a una distancia “d/2” a partir del paño de la columna en ambas direcciones, según se muestra en la Figura 7.
2.3.3.1. Fuerza cortante por penetración para la columna 1
La fuerza cortante por penetración de la columna 1 “Vp1” que actúan sobre la zapata es la fuerza “P1” menos el área rectangular formada por los puntos 5, 6, 7 y 8, esta se muestra como sigue:
2.3.3.2. Fuerza cortante por penetración para la columna 2
La fuerza cortante por penetración de la columna 2 “Vp2” que actúan sobre la zapata es la fuerza “P2” menos el área rectangular formada por los puntos 9, 10, 11 y 12, esta se muestra como sigue:
3. Ejemplo numérico
El diseño de una zapata combinada rectangular de lindero con dos lados opuestos restringidos que soporta dos columnas cuadradas se presenta en la Figura 2, con la información básica siguiente: Columna 1 = 40x40 cm; Columna 2 = 40x40 cm; L = 5.60 m; H = 2.0 m; PD1 = 600 kN; PL1 = 400 kN; MDx1 = 140 kN-m; MLx1 = 100 kN-m; MDy1 = 120 kN-m; MLy1 = 80 kN-m; PD2 = 500 kN; PL2 = 300 kN; MDx2 = 120 kN-m; MLx2 = 100 kN-m; MDy2 = 110 kN-m; MLy2 = 90 kN-m; f’c = 21 MPa; fy = 420 MPa; qa = 220 kN/m2 ; γppz = 24 kN/m3 ; γpps = 15 kN/m 3.
Dónde: H es la profundidad de la zapata, PD es la carga muerta, PL es la carga en viva, MDx es el momento alrededor del eje “X-X” de la carga muerta, MLx es el momento alrededor del eje “X-X” de la carga viva, MDy es el momento alrededor del eje “Y-Y” de la carga muerta, MLy es el momento alrededor del eje “Y-Y” de la carga viva.
El diseño se realiza empleando el criterio de resistencia última, y se obtiene mediante el procedimiento usado por Luévanos-Rojas (2014b).
Paso 1: Las cargas y momentos que actúan sobre el suelo son: P1 = 1000 kN; Mx1 = 240 kN-m; My1 = 200 kN-m; P2 = 800 kN; Mx2 = 220 kN-m; My2 = 200 kN-m; R = 1800 kN; MyT = 400 kN-m; MxT = 1020 kN-m.
Paso 2: La capacidad de carga disponible del suelo: Se propone un espesor “t” de la zapata, la primera propuesta es el espesor mínimo de 25 cm de acuerdo con el reglamento del ACI, posteriormente, el espesor es revisado para cumplir con las condiciones: momentos, cortante por flexión y cortante por penetración. Si estas condiciones no se cumplen, se propone un espesor mayor, hasta que las tres condiciones mencionadas se satisfagan. El espesor de la zapata que cumple las tres condiciones mencionadas anteriormente es de 85 cm. Utilizando la ecuación (6) se obtiene la capacidad de carga disponible del suelo “σadm ” es 182.35 kN/m2.
Paso 3: El valor de “a” por la ecuación (2) se obtiene: a = 6.00 m. El valor de “b” por la ecuación (4) se encuentra: b = 3.08 m, y por la ecuación (5) se obtiene: b = 3.25 m. Por lo tanto, las dimensiones de la zapata son: a = 6.00 m y b = 3.30 m.
Paso 4: Los elementos mecánicos (P, Mx, My) que actúa sobre la zapata se factorizan: Pu1 = 1360 kN; Mux1 = 328 kN-m; Muy1 = 272 kN-m; Pu2 = 1080 kN; Mux2 = 304 kN-m; Muy2 = 276 kN-m; R = 2440 kN; MuyT = 548 kN-m; MuxT = 1416 kN-m.
Paso 5: Los momentos que actúan sobre la zapata. Los momentos alrededor de los ejes paralelos al eje Y-Y son: Ma-a = 544.64 kN-m; Mb-b = 457.08 kN-m. Los momentos alrededor de los ejes paralelos al eje X-X son: Mc-c = ‒549.43 kN-m; Md-d = ‒1652.53 kN-m; Me-e = +102.49 kN-m.
Paso 6: La profundidad efectiva (peralte efectivo). El peralte efectivo para el momento máximo de los ejes paralelos al eje Y-Y es: d = 37.61 cm. El peralte efectivo para el momento máximo de los ejes paralelos al eje X-X es: d = 31.95 cm. Profundidad efectiva después de realizar diferentes propuestas es: d = 77.00 cm, r = 8.00 cm, t = 85.00 cm.
Paso 7: La fuerza cortante por flexión (fuerza cortante unidireccional). Las fuerzas cortantes en los ejes paralelos al eje Y-Y, la fuerza cortante por flexión permitida es: ∅v Vcf = 400.26 kN; las fuerzas cortantes por flexión actuantes son: Vff-f = 361.15 kN; Vfg-g = 304.64 kN. Por lo tanto cumple. Las fuerzas cortantes en los ejes paralelos al eje X-X, la fuerza cortante por flexión permitida es: ∅v Vcf = 1682.60 kN; las fuerzas cortantes por flexión actuantes son: Vfh-h = 1176.23 kN; Vfg-g = ‒ 826.48 kN. Por lo tanto cumple.
Paso 8. La fuerza cortante por penetración (fuerza cortante bidireccional). La fuerza cortante por penetración permitida es: ∅v Vcp = 4191.22 kN; ∅v Vcp = 7114.75 kN; ∅v Vcp = 2711.96 kN. La fuerza cortante por penetración actuante: Para la columna 1 es: Vcp1 = 1189.73 kN. Para la columna 2 es: Vcp2 = 1023.91 kN. Por lo tanto cumple.
Paso 9. El acero de refuerzo. w = 0.0425.
-
El acero de refuerzo longitudinal (acero de refuerzo en la dirección del eje “Y”).
El acero de refuerzo en la parte superior: Asp = 58.35 cm2. A smin = 84.62 cm2. Por lo tanto se propone acero mínimo por flexión “Asmin”. Usar 17 varillas de 1” (2.54 cm) de diámetro.
El acero de refuerzo en la parte inferior: Asp = 3.53 cm2. Asmin = 84.62 cm2. Por lo tanto se propone acero mínimo por flexión “Asmin”. Usar 17 varillas de 1” (2.54 cm) de diámetro.
-
El acero de refuerzo transversal (acero de refuerzo en la dirección del eje “X”):
El acero de refuerzo en la parte inferior: Bajo la columna 1: Asp = 19.45 cm2. Asmin = 20.13 cm2. Por lo tanto, se propone acero mínimo por flexión “Asmin”. Usar 8 varillas de 3/4” (1.91 cm) de diámetro. Bajo la columna 2: Asp = 16.22 cm2. Asmin = 20.13 cm2. Por lo tanto, se propone acero mínimo por flexión “Asmin ”. Usar 8 varillas de 3/4” (1.91 cm) de diámetro.
El acero de refuerzo en la parte excedente de las columnas: Se propone acero por temperatura: Ast = 0.0018bw t = 67.78 cm2. Usar 24 varillas de 3/4” (1.91 cm) de diámetro.
El acero de refuerzo en la parte superior: Se propone acero por temperatura: Ast = 0.0018bw t = 91.80 cm2. Usar 33 varillas de 3/4” (1.91 cm) de diámetro.
Paso 10. La longitud de desarrollo para barras corrugadas:
a) Acero de refuerzo en la parte superior
dónde: ψt = 1.3 ya que tiene más de 30 cm de concreto fresco por debajo del refuerzo, ψe = λ = 1.
La longitud disponible en la dirección longitudinal de la zapata es: 300 - 50.19 - 8 = 241.81 cm.
Entonces, la longitud de desarrollo es menor que la longitud disponible. Por lo tanto, no requiere gancho.
b)Acero de refuerzo en la parte inferior
dónde: ψ t = 1, ψ e = λ = 1.
La longitud disponible en la dirección longitudinal de la zapata es: 330/2 - 40/2 - 8 = 137 cm.
Entonces, la longitud de desarrollo es menor que la longitud disponible. Por lo tanto, no requiere gancho.
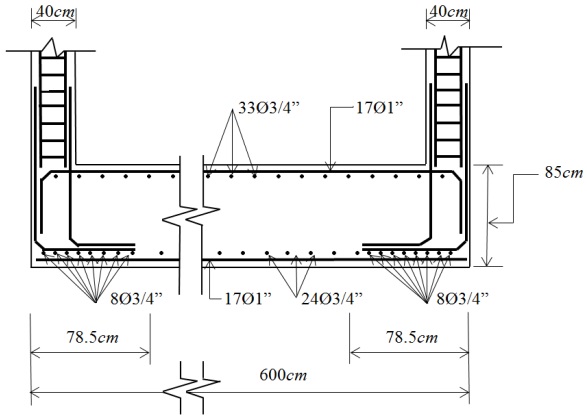
Las dimensiones y el acero de refuerzo de la zapata combinada rectangular de lindero soportando dos columnas cuadradas con dos lados opuestos restringidos se muestran en la Figura 8.
4. Conclusiones
El modelo presentado en este documento sólo se aplica para el diseño de zapatas combinadas rectangulares de lindero con dos lados opuestos restringidos soportando dos columnas. Se supone que el suelo bajo la zapata es un material elástico y homogéneo, y la zapata es rígida, que cumplen con la expresión de la flexión bidireccional, es decir, la variación de la presión es lineal.
Las ecuaciones propuestas ofrecen directamente las dimensiones en planta de la cimentación, garantizando además que la presión admisible en el terreno no será excedido. Por otro lado, los elementos mecánicos para momentos, fuerza cortante por flexión (fuerza cortante unidireccional) y fuerza cortante por penetración (fuerza cortante bidireccional), también pueden diferir de los obtenidos con una presión constante del terreno. En este trabajo, se proponen también expresiones para obtenerse estos elementos de diseño en forma sistemática.
El modelo propuesto presentado en este documento se puede aplicar a los tres tipos de zapatas combinadas rectangulares de lindero con dos lados opuestos restringidos en términos de las cargas aplicadas a cada columna: 1) Carga axial concéntrica, 2) Carga axial y momento en uno dirección (flexión unidireccional), 3) Carga axial y momento en dos direcciones (bidireccional flexión).
Las sugerencias para futuras investigaciones: 1) Cuando las zapatas combinadas rectangulares de lindero con dos lados opuestos restringidos soporten más de dos columnas; 2) Cuando se presenta otro tipo de suelo, por ejemplo en suelos totalmente cohesivos (suelos arcillosos) y suelos totalmente granulares (suelos arenosos), el diagrama de presión no es lineal y deben ser tratados de manera diferente (Figura 1); 3) Cuando el caso de que no toda la base de la cimentación genere compresiones en el suelo, trabajando sólo parcialmente su superficie de contacto, lo cual está permitido en algunas hipótesis de carga infrecuentes, sobre todo en cimentaciones de equipos industriales, cuya solución es iterativa (Bowles, 1970).











 texto en
texto en