Elementos finitos con discontinuidades interiores mejorados para simular el daño en sólidos

 

Juárez-Luna G.¹ y Ayala G.²

 

¹ Profesor-Investigador, Universidad Autónoma Metropolitana, San Pablo No. 180, Col. Reynosa Tamaulipas, Azcapotzalco, C.P. 02200, México, D.F. E-mail: gjl@correo.azc.uam.mx

² Profesor-Investigador, Instituto de Ingeniería, Universidad Nacional Autónoma de México, Av. Universidad 3000, Ciudad Universitaria, Coyoacán, C.P. 04510, México D.F. E-mail: gayalam@iingen.unam.mx

 

Resumen

Se desarrollan e implantan elementos finitos con discontinuidades interiores con una nueva definición del vector de tracciones, que depende de la discontinuidad y del ángulo. Se realiza un análisis de las principales características de los elementos finitos con discontinuidades interiores; particularmente dos familias de este tipo de elementos: 1) cinemático óptimo simétrico y 2) estático y cinemático optimo no simétrico. Las características analizadas son la formulación variacional, modelo constitutivo de daño y como se introduce la discontinuidad. Se demuestra que la cinemática y el equilibrio se satisfacen sin el problema de tracciones ficticias como se establece en la literatura. Para mostrar la validez de la formulación simétrica, se presentan ejemplos de aplicación numérica para ilustrar el desempeño de la formulación propuesta. Los resultados muestran que la formulación propuesta proporciona resultandos congruentes con la energía requerida para crear una discontinuidad, sin subestimar o sobrestimar esta energía como sucede con las formulaciones no simétricas.

Palabras clave: Discontinuidades interiores, localización de deformaciones, formulación variacional, discontinuidades fuertes, modelo de daño.

 

Abstract

Finite elements with embedded discontinuities with a new definition of traction vector, dependent on the discontinuity length and the angle, are developed and implemented. An analysis of the principal features of finite elements with embedded discontinuities was performed; particularly two families of this kind of elements: 1) kinematically optimal symmetric and 2) statically and kinematically optimal non-symmetric. The analysed features are the variational formulation, damage model and how the discontinuity is introduced. It is shown that kinematics and equilibrium are satisfied, without the problem of fictitious tractions as stated in the literature. To show the validity of this symmetric formulation, representative numerical examples illustrating the performance of the proposed formulation are presented. The results show that the proposed formulation provides congruent results whit the energy required to create a discontinuity, without overestimate or underestimate this energy as occurs with the non-symmetric formulations.

Keywords: Embedded discontinuities, strain localization, variational formulation, strong discontinuity, damage model.

 

Resumo

Desenvolvem-se e implantam elementos finitos com descontinuidades interiores com uma nova definição do vector de trações, que depende da descontinuidade e do ângulo. Realiza-se uma análise das principais características dos elementos finitos com descontinuidades interiores; particularmente duas famílias deste tipo de elementos: 1) cinemático ótimo simétrico e 2) estático e cinemático ótimo não simétrico. As características analisadas são a formulação variacional, modelo constitutivo de dano e como se introduz a descontinuidade. Demonstra-se que a cinemática e o equilíbrio se satisfazem sem o problema de trações fictícias como se estabelece na literatura. Para mostrar a validez da formulação simétrica, apresentamos exemplos de aplicação numérica para ilustrar o desempenho da formulação proposta. Os resultados mostram que essa formulação proporciona resultados congruentes com a energia requerida para criar uma descontinuidade, sem subestimar ou sobrestimar esta energia como acontece com as formulações não simétricas.

Palavras chave: Descontinuidades interiores, localização de deformações, formulação variacional, descontinuidades fortes, modelo de dano.

 

1. INTRODUCCIÓN

La idea de concentrar deformaciones en una línea o una superficie en problemas cuasi-estáticos de la mecánica del daño en 2D ó 3D, respectivamente, ha motivado el desarrollo y aplicación de elementos finitos sólidos con discontinuidades interiores (EFDI), e.g., Ortiz et al. (1987), Simo y Rifai (1990), Simo et al. (1993), Simo y Oliver (1994), Oliver (1996), Juárez y Ayala (2009), Dias-da Costa et al. (2009a), Dias-da Costa et al. (2009b), Dujc et al. (2010a), Dujc et al. (2010b), Contrafatto et al. (2012a), Contrafatto et al. (2012b), Dujc et al. (2013a), Juárez-Luna y Ayala (2014) entre otros. Una extensión de esta técnica, es el desarrollo de elementos finitos para simular articulaciones en vigas, e.g., Armero y Ehrlich (2006a), Ehrlich y Armero (2005), Juárez y Ayala (2012) y Dujc et al. (2013b); y una formulación extendida para el análisis de líneas de articulaciones (bisagras) con ablandamiento por Armero y Ehrlich (2006b). Recientemente, los EFDI se han utilizado en simulaciones para fractura de problemas dinámicos, e.g., Huespe et al. (2006), Armero y Linder (2008), Armero y Linder (2009). En la formulación de este tipo de elementos, existen dos requisitos que se deben satisfacer en la zona de localización: 1) equilibrio, continuidad de tracciones sobre la interface discontinua y 2) cinemática, movimiento relativo de cuerpo rígido de las dos porciones en que el elemento queda dividido por la discontinuidad (grieta).

Jirásek (2000) realizó un estudio comprensivo de los EFDI, quién los clasificó en tres familias: 1) estáticamente óptimo simétrico (EOS), el cual satisface el equilibrio, pero no la cinemática; 2) cinemáticamente óptimo simétrico (COS), el cual satisface la cinemática, pero aparentemente no satisface el equilibrio; y 3) estáticamente y cinemáticamente óptimo no simétrico (ECON), que satisface ambos, equilibrio y cinemática. Nuevos EFDI simétricos, incluyendo formulaciones mixtas y técnicas de deformación enriquecida, fueron explorados por Oliver et al. (2003), mostrando que aunque estos EFDI simétricos reducen el problema de atoramiento de esfuerzos, la formulación ECON proporciona mejores resultados.

En este artículo se realiza un análisis de las principales características de los EFDI, particularmente de las formulaciones COS y ECON. El equilibrio de la formulación COS se satisface por una nueva definición de las tracciones como función de la longitud de la discontinuidad, tal que las dos ecuaciones de los residuos son fuerzas. La formulación EOS no se incluyó en este artículo puesto que su cinemática es incorrecta, contrario a la formulación de los modelos de discontinuidades fuertes, donde su buen desempeño se atribuye a su cinemática correcta (de Borst 2001).

El contenido de este artículo se describe a continuación. En la sección 2 se presentan las ecuaciones que definen la cinemática y el problema de valores en la frontera (PVF) de un sólido con discontinuidades. Además, esta sección proporciona los modelos constitutivos que describen el comportamiento del material en el continuo y en la zona de discontinuidad para el desarrollo de las discontinuidades. La sección 3 presenta los funcionales de energía para sólidos con discontinuidades fuertes para las formulaciones COS y ECON. La sección 4 muestra la aproximación con elementos finitos de las formulaciones variacionales con discontinuidades fuertes. En la sección 5 se presentan ejemplos numéricos de elementos finitos con discontinuidades, que validan la formulación propuesta. Finalmente, las conclusiones derivadas de este trabajo y sugerencias se proporcionan en la sección 6.

 

2. DEFINICIÓN DEL PROBLEMA

2.1 PVF

Considere un continuo en 3D, definido por un dominio abierto W∈R³, y frontera Γ, como se muestra en la figura 1a, el cual se carga hasta que se tiene una discontinuidad de desplazamientos, [|u|], sobre una superficie, S, donde las deformaciones inelásticas se concentran. Esta discontinuidad divide el dominio en subdominios tal que, Ω= Ω^-+ Ω⁺+S, con dos fronteras, Γ= Γ^-+ Γ⁺. Las condiciones en la frontera son las tracciones, t*, en Γ_σ= Γ_σ^- + Γ_σ⁺, y los desplazamientos prescritos, u*, en Γ_u= Γ_u^- + Γ_u⁺ , tal que Γ_σ UΓ_u=Γ y Γ_σ Γ_u = Ø. Este problema se puede idealizar utilizando dos distintas aproximaciones: discontinuidades fuertes (DF) y discontinuidades discretas (DD). La primera aproximación considera que Ω se mantiene continuo después de iniciar [|u|] (Fig. 1b), con un comportamiento del material descrito por una ecuación constitutiva esfuerzo deformación no lineal. La segunda aproximación considera que Ω deja de ser continuo, debido al desarrollo de S (Fig. 1c) y que existe transmisión de tracciones, relacionadas con [|u|], a través de los bordes de la discontinuidad. Consecuentemente, el comportamiento constitutivo del material en la discontinuidad se describe por una relación constitutiva tracción-salto, mientras que el resto del dominio, Ω / S = Ω⁺ +Ω^- , se describe por relaciones constitutivas estándar.

El campo discontinuo de desplazamiento u, con un salto [|u|] a un punto (material) dado S, induce un campo de deformaciones no acotado. Ambos campos se pueden expresar como:

Donde: ū es la parte continua de los desplazamientos, la parte continua de las deformaciones, H_s es la función de Heaviside definida en S (H_s (x)=0 ∀∈x Ω^- y H_s (x)=1 ∀∈x Ω⁺, δ_s es la función delta de Dirac y ⊗ representa el
producto ádico de los vectores [|u|] y n.

El PVF de las formulaciones DF y DD se define por las ecuaciones y condiciones en la frontera siguientes:

Haga clic para agrandar

Donde: b es el vector de fuerzas, ν es el vector normal a la frontera Γ_σ y n el vector normal a la discontinuidad. En la formulación DF, las tracciones dadas en la Ecuación 2ƒ, se calculan de la proyección de los esfuerzos σ_s, obtenidos de una ley constitutiva esfuerzo-deformación, mientras que en la formulación DD, estas tracciones se calculan directamente de relaciones tracción-desplazamiento.

 

2.2 MODELOS CONSTITUTIVOS

2.2.1 MODELOS DE DAÑO

El modelo de daño continuo isotrópico (Fig. 2a), generalmente utilizado para la formulación ECON, se define por Simo y Ju (1987) y Oliver (2000) como:

 

Haga clic para agrandar

 

Donde: Ψ es la densidad de energía libre, Ψ₀ es la densidad de energía de deformación, ε es el tensor de deformaciones, σ es el tensor de esfuerzos y C es el tensor elástico. La variable de daño d se define en términos de la variable de endurecimiento/ablandamiento q, que depende del parámetro de endurecimiento/ablandamiento, H. El multiplicador de daño γ determina las condiciones de carga-descarga, la función ƒ(τ_σ,q), limita el dominio elástico definiendo la superficie de daño en el espacio de esfuerzos. El valor, r_o, es el umbral que determina el dominio elástico inicial en función de la variable interna r; el punto sobre las variables indica la razón de cambio (derivada) respecto a las deformaciones.

En la aproximación de los desplazamientos y deformaciones del modelo de discontinuidades fuertes, se tiene el modelo de daño discreto (Fig. 2b) siguiente:

Haga clic para agrandar

Donde: ф es la densidad de energía libre discreta, T es el vector de tracción. La variable de daño ω se define en términos de la variable de endurecimiento/ablandamiento , la cual es dependiente del parámetro de endurecimiento/ablandamiento, . El multiplicador de daño determina la–s condiciones de carga-descarga, la función ƒ( T, q), limita el domino elástico definiendo la superficie de daño en el espacio de tracciones. La transición de un modelo constitutivo continuo a uno discreto se realiza como lo establece Oliver et al. (2002).

Las ecuaciones constitutivas tangentes, en términos de razón de cambio (derivada de σ respecto a ε o derivada de T respecto a [|u|] ), de los modelos definidos en las Ecuaciones 3 y 4 respectivamente son:

Donde: C^T es el operador constitutivo continuo tangente C_d^Ty es el operador discreto tangente, que relaciona la tracción
el salto de desplazamiento en el intervalo de carga no lineal, los cuales se definen, respectivamente, por

y para el intervalo elástico y de descarga :

 

3. FORMULACIONES VARIACIONALES

3.1 FORMULACIONES NO SIMÉTRICAS

La formulación ECON, como la que reportan Armero y Garikipati (1996) y Oliver (1996), entre otros, se definen con base al funcional y la ecuación siguientes:

donde la densidad de energía libre ψ(ε^u), depende de las deformaciones como:

Para demostrar que esta formulación incluye el PVF definido en la Ecuación 2, la primera variación de la Ecuación 8 es:

Como se puede observar en la Ecuación 11, esta variación incluye los incisos c, d y g de la Ecuación 2, mientras que los incisos a, b y e son a priori impuestos y ƒ se prescribe localmente en S mediante la Ecuación 9.

 

3.2 FORMULACIONES SIMÉTRICAS

La aproximación COS se basa en el funcional de desplazamientos como el propuesto por: Lotfi y Shing (1995), Wells y Sluys (2001), Alfaiate et al. (2003) y Juárez y Ayala (2009), i.e.,

donde la densidad de energía libre Ψ(ε^u), depende del campo continuo de deformaciones ε, y la densidad de energía libre discreta, Ψ_s([|u|]), depende del salto, respectivamente, definidas como:

De las cuales el tensor de esfuerzos elástico es:

La primera variación del funcional dado en la Ecuación 12 es:

el cual, a diferencia de la formulación no simétrica, incluye la continuidad de tracción interna del PVF.

 

4. APROXIMACIÓN CON EL MÉTODO DEL ELEMENTO FINITO

4.1 DISCRETIZACIÓN

4.1.1 REGULARIZACIÓN DE LA CINEMÁTICA DE DESPLAZAMIENTOS

No es posible el prescribir las condiciones en la frontera, u* , sólo en uno de los campos de desplazamiento, ū o [|u|]; esta dificultad se resuelve, de acuerdo con Oliver (1996), definiendo el campo de desplazamientos como en la Ecuación 17 mostrado en las figuras 3a y b, i.e.,

 

En consecuencia, el campo de las deformaciones se define como:

donde ŭ es el campo de desplazamientos regulares y M_s(x) es la función dada por:

donde ф(x) es una función continua tal que:

La función M_s, tiene dos propiedades: M_s(x) =1 ∀x ∈S y M_s (x) =0 ∀x∈Ω^- ∪Ω⁺, Cuya representación gráfica se muestra en la Fig. 3c.

El desplazamiento en la parte continua del sólido de la ec. (1) se define ahora como:

la cual puede ser elástica lineal. El campo de deformaciones continuo, , está dado por:

sustituyendo la Ecuación 21 en la Ecuación 22

Si el salto de desplazamiento es constante (Ec. 23), el campo de deformaciones continuas puede rescribirse como:

Para problemas en 2D, el salto de desplazamiento y el vector de tracción se definen en el sistema local n,s o en el sistema global x,y como se muestra en la figura 4, los cuales se expresan respectivamente como:

 

Donde R se define como:

La tracción T_x,yen el sistema global se determina como:

 

4.1.2 APROXIMACIÓN DE LOS CAMPOS DE DESPLAZAMIENTOS Y DEFORMACIONES

El campo de desplazamiento regular se aproxima como:

Donde: N es el vector estándar de las funciones de forma del elemento

y d es el vector de desplazamientos nodales. La función, M_s(x), se define en la aproximación del elemento finito como:

Donde: ф^e se construye mediante:

Donde: N_i+ son las funciones de forma correspondientes a los nodos localizados en Ω⁺ del elemento finito que contiene la discontinuidad, de acuerdo con la definición de ф (Ec. 20).
El campo de desplazamientos definido (Ec. 17) está dado por:

El campo de deformaciones continúas en la (Ec. 23) se aproxima como:

El campo de deformaciones no acotadas:

Donde: B, es la matriz de interpolación estándar, que contiene las derivadas de las funciones de forma estándar ∂(Nd)=Bd
y ⊗ representa el producto diádico de los vectores n y [|u|]_x,y.

 

4.2 APROXIMACIÓN DE LA FORMULACIÓN NO-SIMÉTRICA

Sustituyendo las Ecuaciones 33 y 34 en el funcional de energía (Ec. 8), derivando con respecto a d, igualando a cero y aproximando la Ecuación 9:

En las Ecuaciones 36 y 37, σ es no lineal, su linealización con series de Taylor proporciona:

Se puede demostrar que R₁ (Ec. 39) representa el equilibrio entre las fuerzas externas e internas en el dominio Ω\S, mientras que R₂ (Ec. 40) representa el equilibrio entre las fuerzas en el dominio Ω\S y las fuerzas en la discontinuidad Γ_s.

 

4.3 APROXIMACIÓN DE LA FORMULACIÓN SIMÉTRICA

Las ecuaciones de equilibrio correspondiente a esta formulación se obtienen sustituyendo las Ecuaciones 33 y 34 en el funcional de energía (Ec. 12), e igualando a cero su derivada respecto a las variables d y [|u|],

Puesto que en las Ecuaciones 41 y 42 σ(ε)^- y T_x,y son no lineales, sus respectivas linealizaciones con series de Taylor proporcionan:

donde R₃y R₄ se define como:

Para reducir el tamaño del sistema dado (Ec. 43), los grados de libertad adicionales, Δ[|u|], pueden condensarse. En la Ecuación 44, R₃ representa el equilibrio entre las fuerzas externas y las fuerzas internas en el dominio Ω\S, mientras que R₄, en la Ecuación 45, representa el equilibrio entre las fuerzas en el dominio Ω\S y las fuerzas en la discontinuidad Γ_S. La diferencia entre la Ecuación 40 y Ecuación 45 es que en la primera, los esfuerzos en la discontinuidad se determinan por una ley constitutiva esfuerzo-deformación y R₂ tiene unidades de fuerza/longitud², mientras que en la última, las tracciones se calculan por una ley constitutiva tracción-salto y R₄ tiene unidades congruentes de fuerza.

 

5. EJEMPLOS NUMÉRICOS

5.1 ELEMENTO TRIANGULAR CON DISCONTINUIDAD PARALELA AL BORDE

Un elemento triangular de deformación constante, (Fig. 5a), se le aplica una fuerza horizontal en el nodo 3 y se restringe en ambas direcciones en los nodos 1 y 2. Las propiedades mecánicas del material son: módulo de Young, E=1000 MPa, relación de Poisson ν=0.0, esfuerzo máximo a tensión, σ_u=1 MPa, y densidad de energía de fractura G_ƒ=0.005MN/m. Este elemento se analizó considerando que la discontinuidad ocurre en diferentes ubicaciones (Fig. 5a - 5d), i.e., la discontinuidad tiene diferentes longitudes: 1_d1=0.2, 1_d2=0.5 y 1_d3=0.8, respectivamente.

El modelo de daño discreto, dado por la Ecuación 4, se utilizó para describir el comportamiento del material de este elemento. La tracción T_x,y se determinó con la Ecuación 28 y la máxima tracción a tensión considerada fue t_u=1 MPa. Como se puede observar en la Fig. 6, las curvas carga P contra desplazamiento d para las longitudes de discontinuidad 1_d1 y 1_d3, presentan inestabilidades numéricas cuando t_n, calculado con la Ecuación 28, alcanza la tracción a tensión máxima t_u=1 MPa, mientras que la curva para 1_d2 no presente problemas numéricos.

Las inestabilidades numéricas se atribuyen a que en la Ecuación 45, R₄ no se impone que sea igual a cero, el cual para este ejemplo corresponde a:

El triángulo de deformación constante, (Fig. 5a), tiene B_c^T=0.5, A_e = 1 y t_y =0, por lo que (Ec. 46) se rescribe como:

Donde: σ_x y t_x corresponden a los valores de tensión máxima, i.e.,

Algunas observaciones de estos resultados son:

• Aparentemente, el equilibrio en la (Ec. 46) sólo se satisface si la longitud de la discontinuidad es 1_d = (y₁ –y₂) / 2 y paralela al borde del elemento como lo establece Jirásek (2000).

• La Fig. 6 muestra que las áreas debajo de las curvas son distintas para cada longitud de la discontinuidad, de acuerdo con la energía necesaria para producir discontinuidades.

• La localización inicia cuando t_n>t_u , donde t_n se calcula del esfuerzo efectivo σ, de la (Ec. 28). Esta observación es válida para cualquier tipo de elemento, incluyendo el triángulo de deformación constante, utilizado en esta formulación. Por lo que, las curvas en la Fig. 6 muestran que el valor efectivo de la tracción T , cuando ocurre t_u, no sólo depende de σ, sino también de la longitud de la discontinuidad, 1_d, y del ángulo θ.

Este ejemplo muestra aparentemente que el equilibrio se satisfice si la longitud de la discontinuidad es 1_d = (y₁ – y₂) /2 y se ubica paralelamente al borde del elemento. Sin embargo, lo que en realidad se muestra es que la longitud de la discontinuidad y el ángulo se definen para satisfacer el equilibrio. No obstante, una ventaja de esta formulación es que las deformaciones por cortante no se presentan, y tampoco el salto de desplazamientos tangenciales como lo reporta Jirásek (2000).

 

5.1.1 ESTRATEGIA NUMÉRICA PARA GARANTIZAR EL EQUILIBRIO EN LA DISCONTINUIDAD

Para logar consistentemente el equilibrio en la formulación COS, las fuerzas R₃ y R₄ dadas en las Ecuaciones 44 y 45, deben igualarse a cero. Particularmente, la última ecuación, la cual se expresa como:

Considerando que las tracciones en la discontinuidad son valores constantes dentro de este elemento, la Ecuación 49 se convierte en:

la cual, en sistema local, es:

la definición de tracción dada (Ec. 50) es diferente a la propuesta por Sancho et al. (2007):

Donde: A_e es el área del elemento y n⁺ el vector unitario de un borde.

 

5.1.2 ELEMENTO TRIANGULAR DE DEFORMACIÓN CONSTANTE

En un elemento triangular de deformación constante, con base (Ec. 51), la relación entre σ y T_n,s es:

Sustituyendo los valores de R, R_c^T y σ para un elemento triangular de deformación constante (Ec. 54) y después de operaciones algebraicas:

Para el ejemplo descrito en la sección 5.1, los valores de tracción de los triángulos (Fig. 5) son:

Así, en la Ecuación 56, la tracción normal t_n, es inversamente proporcional a la longitud de la discontinuidad, i.e., para 1_d1, t_n=2.5σ_xx; para 1_d2, t_n=1.0σ_xx; y para 1_d3, t_n=0.625σ_xx, (Fig. 7).

Utilizando la Ecuación 56 para calcular t_n en el problema del triángulo descrito en la sección 5.1, las curvas de la carga P contra el desplazamiento d se muestran en la Fig. 8, donde se puede observar que las áreas bajo cada una de ellas son distintas, un resultado consistente con la física del problema, porque a mayor longitud de la discontinuidad, mayor energía necesaria para crearla.

Note que la misma carga máxima, correspondiente a 1_d2, se obtendría para las tres longitudes de la discontinuidad con una formulación no simétrica como la de Armero y Garikipati (1996) y Oliver (1996), puesto que en el criterio de daño, ni el estado de esfuerzos σ, ni el ángulo θ dependen de la longitud de la discontinuidad. La misma conclusión la obtuvieron Alfaiate et al. (2003), quienes implementaron saltos de desplazamiento no-homogéneos en EFDI.

La forma promediada en que Armero y Garikipati (1996) y Oliver (1996) imponen la continuidad interna de tracciones es:

La cual en su aproximación con elementos finitos proporciona, después de su integración, una ecuación idéntica a la (Ec. 28). Este resultado, como se muestra en la Fig. 8, puede sobrestimar o subestimar la energía requerida para crear una discontinuidad.

 

5.2 ELEMENTO TRIANGULAR CON DISCONTINUIDAD NO PARALELA AL BORDE

La figura 9a muestra un elemento triangular constante con las mismas propiedades mecánicas del ejemplo en la sección 5.1. Al realizar un análisis elástico, imponiendo un desplazamiento horizontal d=0.000634755 en el nodo 2, los esfuerzos obtenidos son: σ_x=0.413251, σ_y=0.082650 y σ_xy=-0.198361; con estos esfuerzos, la dirección principal es θ =-25.097°. Posteriormente, se realizaron análisis no lineales de este elemento con tres ubicaciones distintas de la discontinuidad, colocada en dirección perpendicular al esfuerzo principal, (Fig. 10), las longitudes de las discontinuidades son: 1_d1=0.179, 1_d2=0.358 y 1_d3=0.534. En este ejemplo, las discontinuidades no son paralelas al borde del elemento. Las curvas de carga P contra el desplazamiento d para cada discontinuidad se muestran en la figura 10, que a diferencia de los resultados mostrados en la figura 6, estos casos no muestran problemas numéricos cuando se alcanza la tracción última a tensión t_n, no obstante persisten diferentes áreas debajo de las curvas P contra d.

 

5.3 ANÁLISIS DE DEFORMACIONES

Para demostrar que la formulación propuesta no produce deformaciones espurias, las deformaciones continúas en un elemento triangular de deformación constante con una discontinuidad, de la (Ec. 34): es:

Considerando el caso del elemento mostrado en la Fig. 11, donde los nodos 2 y 3 se consideran restringidos y se desplaza el nodo 1, las componentes del salto de la discontinuidad son:

La función ф^e para este ejemplo, corresponden a la función de interpolación N₁, dado por:

Sustituyendo las Ecuaciones 60 y 61 en la Ecuación 59, las componentes de deformación son:

Haga clic para agrandar

Puesto que las deformaciones continuas (Ec. 62) son nulas, no existen esfuerzos dentro del elemento. Esta situación corresponde a un elemento completamente dañado con cinemática y equilibrio satisfecho naturalmente. Las Ecuaciones 56 y 57 muestran además que en la formulación propuesta no se presentan tracciones ficticias como lo establece Jiráseck (2000).

 

5.4 ESPÉCIMEN EN TENSIÓN

En este ejemplo, un elemento de sección rectangular en tensión se idealiza como una placa en 2D de espesor t=10, con las dimensiones y condiciones mostradas en la figura 12, la cual se restringe en su borde izquierdo y se estira en el borde derecho. Para este ejemplo, las propiedades del material, reportadas por Chaves (2003), son: módulo de Young, E=20000, relación de Poisson ν=0, esfuerzo máximo a tensión, σ_u=1 y densidad de energía de fractura Gƒ=0.18. En el análisis se consideraron condiciones de esfuerzo plano y un ablandamiento lineal. Un valor nulo de la relación de Poisson fue necesario para garantizar la equivalencia del problema de una placa en 2D y el problema de una barra en 1D. Una vez que se alcanzó la superficie de daño, la falla en el material iniciaría en todos los puntos de la placa, puesto que el estado de esfuerzos es constante; sin embargo, con el propósito de ilustrar la falla en la malla de la figura 13a, la discontinuidad fue colocada artificialmente en el centro de la placa como se muestra en la figura 13b.

La figura 14 muestra la evolución de la carga P, contra el desplazamiento, δ, aplicado en el borde derecho de la placa. Como se puede observar, los resultados numéricos obtenidos con la formulación propuesta son iguales a aquellos reportados por Chaves (2003), obtenidos con la formulación ECON, mediante elementos tetraedros. En este caso, ambos resultados fueron los mismos porque la longitud total de la discontinuidad es la misma y el salto de desplazamiento es uniforme.

 

5.5 ESPÉCIMEN EN CORTANTE

Un espécimen rectangular, con geometría y condiciones de frontera mostradas en la figura 15, se somete a una carga horizontal aplicada en la parte superior. Debido a que el espécimen está restringido a la mitad de su altura, los esfuerzos cortantes se concentran a lo largo de su eje longitudinal. Las propiedades del material son: módulo de Young E=26,500 kPa, relación de Poisson ν=0.3, esfuerzo máximo a cortante τ_u=20 kPa, módulo de rigidez a cortante μ=10,000 kPa y densidades de energía de fractura a cortante G_f1= 52.083 N/m y G_f2 =100N/m.

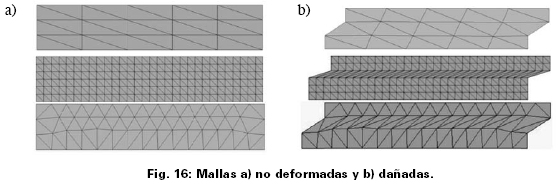
Para la simulación de este espécimen se utilizaron tres mallas de elementos triangulares en 2D (Fig. 16), las primeras dos estructuradas y la última no estructurada. Las curvas carga contra desplazamiento obtenidos con la formulación propuesta coinciden con los resultados numéricos reportados por Borja (2000), quién también utilizó un modelo de discontinuidades interiores de la familia ECOS, el área debajo de estas curvas (Fig. 17), coincide con la energía de fractura necesaria para formar esta discontinuidad. Es de interés mencionar que Borja (2000) utilizó una superficie de plasticidad con ablandamiento, tomando el esfuerzo cortante último como el esfuerzo de fluencia. Al igual que en el ejemplo anterior, aunque este en modo de falla II, ambos resultados fueron los mismos con ambas formulaciones porque la longitud total de la discontinuidad es la misma y el salto de desplazamientos es uniforme.

5.6 PROBLEMA DE ESTABILIDAD DE UN TALUD

Se analiza un problema considerado más complejo, el cual fue reportado por Oliver et al. (2006). Este consiste en un talud con una zapata rígida localizada en la parte superior, con las dimensiones y condiciones en la frontera (Fig. 18). Las propiedades mecánicas del suelo son: módulo de Young E= 10 MPa, relación de Poisson υ=0.45, esfuerzo último a tensión σ_u=100 kPa y densidad de energía de fractura Gƒ=80 MN/m. En el análisis se aplicó un desplazamiento hacia abajo en el centro de la zapata. La malla estructurada (Fig. 19a), en la que al alcanzarse la superficie de daño, la falla inicia en el suelo ubicado en la esquina inferior de la zapata, propagándose a lo largo de una trayectoria curva (Fig. 19b).

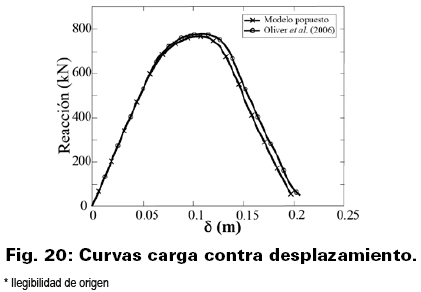
La evolución de la carga, P, contra el desplazamiento, δ, aplicado en el centro de la zapata se muestra en la figura 20, donde se observa que los resultados numéricos reportados por Oliver et al. (2006) muestran que la formulación ECON puede sobreestimar la energía requerida para crear la línea de deslizamiento, lo cual se atribuye a que la formulación ECON no incluye la longitud de la discontinuidad como la formulación propuesta lo hace. En realidad, la longitud total de la discontinuidad calculada con la formulación propuesta puede ser más corta que la calculada con la formulación ECON.

 

6. CONCLUSIONES

Este artículo muestra que la formulación COS propuesta satisface no sólo la cinemática relativa al movimiento de cuerpo rígido de las dos partes en la que queda dividido el elemento por la discontinuidad, sino también el equilibrio correspondiente a la continuidad de tracciones sobre la discontinuidad.

La continuidad interna de tracciones proporciona una definición del vector de tracciones en la discontinuidad, dependiente de la longitud y de la orientación de la discontinuidad.

Se mostró que en la formulación ECON, un residuo tiene unidades de fuerza y el otro tiene unidades de fuerza/longitud², mientras que en la formulación COS, ambos residuos tienen unidades de fuerza.

Se demostró que esta formulación, miembro de la familia COS de EFDI, no induce tracciones espurias cuando la discontinuidad se encuentra en dirección perpendicular al esfuerzo principal.

Se demostró que la familia ECON puede sobre o subestimar la energía requerida para crear una discontinuidad, puesto que este efecto se relaciona con la longitud total de la discontinuidad, lo cual no se nota cuando la trayectoria de la discontinuidad es una línea recta.

Cuando se considera la longitud de la discontinuidad en el análisis, la energía requerida para crear una discontinuidad puede ser menor que la calculada con la formulación ECON, puesto que esta energía está directamente relacionada con la longitud de la trayectoria que sigue la discontinuidad.

En los ejemplos del espécimen a tensión y a cortante, los resultados obtenidos con las formulaciones COS y ECON fueron idénticos porque la longitud total de las discontinuidades son las mismas y el salto de los desplazamientos son uniformes, fallando en los modos I y II, respectivamente. Sin embargo, el problema de estabilidad de un talud en modo de falla II, se muestra que la formulación ECON puede sobreestimar la energía requerida para crear la línea de deslizamiento, lo cual se atribuye a que la longitud total de la discontinuidad calculada con la formulación COS puede ser más corta que la calculada con la formulación ECON.

 

AGRADECIMIENTOS

El primer autor agradece el apoyo dado por la Universidad Autónoma Metropolitana y al proyecto 182736: "Análisis y diseño de losas de concreto" auspiciado por la Secretaría de Educación Pública y al Consejo Nacional de Ciencia y Tecnología. El segundo autor agradece el apoyo dado por Dirección General Asuntos del Personal Académico de la Universidad Nacional Autónoma de México por el patrocinio del proyecto PAPIIT-IN108512. Además, se agradece la revisión de estilo a Jocelyn Tatiana Hernández Bautista.

 

REFERENCIAS

Alfaiate, J., Simone, A., Sluys, L. J. (2003), "Non-homogeneous displacement jumps in strong embedded discontinuities", International Journal of Solids and Structures, 40(21), pp. 5799-5817.         [ Links ]

Armero, F., Garikipati, K. (1996), "An analysis of strong discontinuities in multiplicative finite strain plasticity and their relation with the numerical simulation of strain localization in solids", International Journal of Solids and Structures, 33(20-22), pp. 2863-2885.         [ Links ]

Armero, F., Linder, C. (2008), "New finite elements with embedded strong discontinuities in the finite deformation range", Computer Methods in Applied Mechanics and Engineering, 197(37-40), pp. 3138-3170.         [ Links ]

Armero, F., Linder, C. (2009), "Finite elements with embedded branching", Finite Elements in Analysis and Design, 45(4), pp. 280-293.         [ Links ]

Armero, F., Ehrlich, D. (2006a), "Numerical modeling of softening hinges in thin Euler-Bernoulli beams, Computers & Structures, 84(10-11), pp. 641-656.         [ Links ]

Armero, F., Ehrlich, D. (2006b), "Finite element methods for the multi-scale modelling of softening hinge lines in plates at failure", Computer Methods in Applied Mechanics and Engineering, 195(13-16), pp. 1283-1324.         [ Links ]

Chaves, E. W. V. (2003), "Athree dimensional setting for strong discontinuities modelling infailure mechanics", Tesis de Doctorado, Escola Tècnica Superior d'Enginyers de Camins, Canals i Ports, Universidad Politécnica de Cataluña, Barcelona, España.         [ Links ]

Contrafatto, L., Cuomo, M., Di Venti, GT. (2012a), "Finite elements with non-homogeneous embedded discontinuities. In: Eberhardsteiner, J. et. al. (Eds.), 6th European Congress on Computational Methods in Applied Sciences and Engineering, ECCOMAS 2012, Vienna, Austria, pp.1-20.         [ Links ]

Contrafatto, L., Cuomo, M., Fazio, F. (2012b), "An enriched finite element for crack opening and rebar slip in reinforced concrete members", International Journal of Fracture, 178(1-2), pp. 33-50.         [ Links ]

Dias-da Costa, D., Alfaiate, J., Sluys, L. J., Júlio, E. (2009a), "Towards a generalization of a discrete strong discontinuity approach", Computer Methods in Applied Mechanics and Engineering, 198, pp. 3670-3681.         [ Links ]

Dias-da-Costa, D., Alfaiate, J., Sluys, L.J., Júlio, E. (2009b), "A discrete strong discontinuity approach", Engineering Fracture Mechanics , 76(9), pp. 1176-1201        [ Links ]

de Borst, R., Wells, G. N., Sluys, L. J. (2001), "Some observations on embedded discontinuity models", Engineering Computations, 18(1-2), pp. 241-254.         [ Links ]

Dujc, J., Brank, B., Ibrahimbegovic, A. (2010a), "Quadrilateral finite element with embedded strong discontinuity for failure analysis of solids", Computer Modeling in Engineering & Sciences, 69(3), pp. 223-260.         [ Links ]

Dujc, J., Brank, B., Ibrahimbegovic, A., Brancherie, D. (2010b), "An embedded crack model for failure analysis of concrete solids", Computers and Concrete, 7(4), pp. 331-346.         [ Links ]

Dujc, J., Brank, B., Ibrahimbegovic, A. (2013a), "Stress-hybrid quadrilateral finite element with embedded strong discontinuity for failure analysis of plane stress solids", International Journal for Numerical Methods in Engineering, 94, pp. 1075-1098.         [ Links ]

Dujc, J., Brank, B., Ibrahimbegovic, A. (2013b), "Embedded discontinuity finite element formulation for failure analysis of planar reinforced concrete beams and frames", Engineering Structures, 50, pp. 115-125.         [ Links ]

Ehrlich, D., Armero, F. (2005), "Finite element methods for the analysis of softening plastic hinges in beams and frames", Computational Mechanics, 435(4), pp. 237-264.         [ Links ]

Huespe, A. E., Oliver, J., Sanchez, P. J., Blanco, S., Sonzogni, V. (2006), "Strong discontinuity approach in dynamic fracture simulations", Mecánica Computacional, XXV, pp. 1997-2018.         [ Links ]

Jirásek M. (2000), "Comparative study on finite elements with embedded discontinuities", Computer Methods in Applied Mechanics and Engineering, 188(1-3), pp. 307-330.         [ Links ]

Juárez, G., Ayala, G. (2009), "Variational formulation of the material failure process in solids by embedded discontinuities model", Numerical Methods for Partial Differential Equations, 25(1), pp. 26-62.         [ Links ]

Juárez, G., Ayala, G. A. (2012), "Finite element variational formulation for beams with discontinuities", Finite Elements in Analysis and Design, 54, pp. 37-47.         [ Links ]

Juárez-Luna, G., Ayala, G. A. (2014), "Improvement of some features of finite elements with embedded discontinuities", Engineering Fracture Mechanics, 118, pp. 31-48.         [ Links ]

Lotfi, H. R., Shing, P. (1995), "Embedded representation of fracture in concrete with mixed finite elements", International Journal for Numerical Methods in Engineering, 38(8), pp. 1307-1325.         [ Links ]

Oliver, J. (1996), "Modelling strong discontinuities in solid mechanics via strain softening constitutive equations, Part 1: Fundamentals, 39(21), pp. 3575-3600. Part 2: Numerical simulation", International Journal for Numerical Methods in Engineering, 39(21), pp. 3601-3623.         [ Links ]

Oliver, J. (2000), "On the discrete constitutive models induced by strong discontinuity kinematics and continuum constitutive equations", International Journal of Solids and Structures, 37(48-50), pp. 7207-7229.         [ Links ]

Oliver, J., Huespe, A. E., Pulido, M. D. G., Chaves, E. (2002), "From continuum mechanics to fracture mechanics: the strong discontinuity approach", Engineering Fracture Mechanics, 69(2), pp. 113-136.         [ Links ]

Oliver, J., Huespe, A. E., Samaniego, E. (2003), "A study on finite elements for capturing strong discontinuities", International Journal for Numerical Methods in Engineering, 56(14) , pp. 2135-2161.         [ Links ]

Oliver, J., Huespe, A. E., Blanco, S., Linero, DL. (2006), "Stability and robustness issues in numerical modeling of material failure with the strong discontinuity approach", Computer Methods in Applied Mechanics and Engineering, 195(52), pp. 7093-7114.         [ Links ]

Ortiz, M., Leroy, Y., Needleman, A. (1987), "A finite element method for localized failure analysis", Computer Methods in Applied Mechanics and Engineering, 61(2), pp. 189-214.         [ Links ]

Sancho, J. M., Planas, J., Cendón, D. A., Reyes, E., Gálvez, J. C. (2007), "An embedded crack model for finite element analysis of concrete fracture", Engineering Fracture Mechanics, 74(1-2), pp. 75-86.         [ Links ]

Simo, J. C., Ju, J. (1987), "Strain and stress based continuum damage models, I. Formulación", International Journal of Solids and Structures, 23(7), pp. 821-840.         [ Links ]

Simo, J. C., Rifai, S. (1990), "A class of mixed assumed strain methods and the method of incompatible modes", International Journal for Numerical Methods in Engineering, 29(8), pp. 1595-1638.         [ Links ]

Simo, J. C., Oliver, J., Armero, F. (1993), "An analysis of strong discontinuities induced by strain-softening in rate-independent inelastic solids", Computational Mechanics, 12(5), pp. 277-296.         [ Links ]

Simo, J. C., Oliver, J. (1994), "A new approach to the analysis and simulation of strain softening in solids", In: Bazant ZP et. al. (Eds.), Fracture and Damage in Quasibrittle Structures, E. and F.N. Spon, London, pp. 25-39.         [ Links ]

Wells, G. N., Sluys, L. J. (2001), "A new method for modelling cohesive cracks using finite elements", International Journal for Numerical Methods in Engineering, 50(12), pp. 2667-2682.         [ Links ]