Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Tecnología y ciencias del agua
On-line version ISSN 2007-2422
Tecnol. cienc. agua vol.11 n.1 Jiutepec Jan./Feb. 2020 Epub May 30, 2020
https://doi.org/10.24850/j-tyca-2020-01-07
Articles
Optimal design of irrigation network shifts and characterization of their flexibility
1Universidad Técnica Particular de Loja, Loja, Ecuador, cmlapo@utpl.edu.ec
2Universidad Politécnica de Valencia, Valencia, España, rperez@gmmf.upv.es
3Universidad de Zaragoza, Zaragoza, España, raliod@unizar.es
4Universidad Politécnica de Valencia, Valencia, España, jmsolano@upv.es
In this contribution, a nonlinear programming genetic hybrid algorithm for the optimal design of pressurized irrigation networks operating in shifts is presented, and an indicator is implemented to evaluate the flexibility of the resulting designs of the hybrid algorithm. The main objective is the minimization of the economic cost of the pipe network and the evaluation of the flexibility of the system designs. The research considers the allocation of shifts to the irrigation outlets (hydrants) and the sizing of the pipes as decision variables to reduce implementation costs. With the results of the optimization, the flexibility of the hydraulic network is analyzed based on the random reassignment of shifts to the hydrants, which simulates the modifications that may occur during network operation. To validate the algorithm, once calibrated, it was applied to the design of four real irrigation sectors of Ecuador and Spain. The results indicate that the designs obtained improve in cost and flexibility with respect to those found with the traditional algorithm of the Economic Series, and that the assignment of the shifts is of utmost importance to minimize investment costs in pipes. At the same time, it constitutes a determining factor in the flexibility of the system
Keywords Optimal network design; genetic algorithm; reliability; non-linear programming; collective irrigation network; hybrid model; genetic operators
En esta contribución se presenta un algoritmo híbrido genético-programación no lineal para el diseño óptimo de redes presurizadas de riego operando a turnos, y se implementa un indicador para evaluar la flexibilidad de los diseños resultantes del algoritmo híbrido. El objetivo principal es la minimización del costo económico de la red de tuberías y la evaluación de la flexibilidad de los diseños del sistema. La investigación considera como variables de decisión la asignación de turnos a las tomas de riego (hidrantes) y el dimensionado de las conducciones para reducir los costos de implementación. Con los resultados de la optimización se analiza la flexibilidad de la red hidráulica con base en la reasignación aleatoria de turno a los hidrantes, que simula las modificaciones susceptibles de ocurrir durante la explotación de la red. Para validar el algoritmo, una vez calibrado, éste fue aplicado al diseño de cuatro sectores de riego reales de Ecuador y España. Los resultados indican que los diseños obtenidos mejoran en costo y flexibilidad respecto a los encontrados con el algoritmo tradicional de la serie económica, y que la asignación de los turnos es de suma importancia para minimizar los costos de inversión en tuberías, lo que a la vez constituye un factor determinante en la flexibilidad del sistema.
Palabras clave diseño óptimo de redes; algoritmo genético; fiabilidad; programación no lineal; red colectiva de riego; modelo híbrido; operadores genéticos
Introduction
In recent decades, irrigated agriculture has increased rapidly due to population growth and the need to ensure optimal crop productivity ((Salazar-Moreno, Rojano-Aguilar, & López-Cruz, 2014). This has driven the development of different irrigation technology systems using pressurized pipes and specific distribution infrastructures to carry the water to each plot. This is the case of the Collective Irrigation Pressure Networks (CIPN). A collective irrigation pressure networks is a system formed by a set of pipes, with generally branched topology allowing the transport of water from its origin to each one of the inlets (hydrants) in the irrigation plots, with sufficient pressure and flow ((Planells, Ortega, Valiente, Montero, & Tarjuelo, 1999). Its advantage over traditional channel-based systems is that they facilitate its construction, are cheaper and provide greater efficiency in the application and control of water. Also, CIPN allow the reduction or elimination of energy costs in drip or sprinkler irrigation.
A CIPN can be designed to operate under two modalities: on-demand or in shifts. The mode of demand irrigation supplies the water at the will of the irrigator (Clément, 1966). The design techniques of the CIPNs operated on-demand define a certain flow limit demanded in each pipeline section, evaluated probabilistically. The design is made in such a way that, for any combination of opening, the resulting pressure at the water inlets is greater than a value of the minimum required pressure height, called Construct Height (H cons). This implies a certain degree of over-dimensioning of the pipes, but in exchange there is total flexibility in intake use.
Meanwhile, the shift model assigns a watering period to each intake in fixed hours. The pipes are sized to transfer the flow strictly required by the open hydrants in the fixed shift. Other combinations of open sockets, even respecting the total flow of the shift, do not guarantee that there is sufficient pressure, higher than the H cons. Therefore, irrigators should limit themselves to watering according to the organization of shifts defined at the time of design. Due to this, the rigidity of use is high. In other words, the flexibility of the system before changes in shifts, endowments, crops, etc., is more reduced than in-demand designs (Espinosa, Flores, Hernández, & Carrillo, 2016). On the other hand, in the CIPN design under the shift modality, there is a strong dependence on the result, in terms of cost and flexibility of use, concerning the allocation of shifts in the project, which is traditionally performed in a heuristic manner.
However, the RCRPs designed to operate in shift mode enjoy properties of interest, since they are generally cheaper by 15% to 50%, because the design implies lower flows than those found in the demand mode. In addition, the shift-designed networks are easier to control, since their uses are predetermined ((Alduán & Monserrat, 2009; Monserrat, Alduán, Cots, & Barragán, 2012).
In this sense, research on specific algorithms for the optimal shift design ((Farmani, Abadia, & Savic, 2007; García et al., 2011) or management (Jiménez, Martínez, Bou, & Bartolí, 2010; Faci et al., 2015; Fernández, Montesinos, Camacho, & Díaz, 2017) of CIPN is still scarce. Finally, the analysis of the CIPN’s flexibility, understanding flexibility as the reliability of the designs resulting from changes in operating conditions, has not been previously contemplated in the case of shift systems (Espinosa et al., 2016). The knowledge advances in these fronts will allow a better shift-operating CIPN design, as well as the identification of the conditions in which these are more favorable.
Over time since the implementation of the first pressurized irrigation systems, different techniques have been developed to optimize CIPN design. Likewise, some authors have studied the reliability and redundancy of the system or water quality to improve the irrigation process ((Lamaddalena, Khadra, & Tlili, 2012). Among them we find analytical-type algorithms offering an optimal solution for the network’s design through a defined number of processes. These algorithms include techniques such as discontinuous optimization of Labye (1966); Nonlinear Programming (NLP) (Theocharis, Tzimopoulos, Yannopoulos, & Sakellariou, 2006); Lagrange Multipliers (Method of the Economic Series-MSE; Deb, 1974) or Linear Programming (PL) ((Pérez, Martínez, & Vela, 1993; Kale, Singh, & Mahar, 2008). All of these methods are effective and of low calculation time when applied to branched networks with pre-established design flows.
On the other hand, evolutionary type algorithms are available, which are part of modern optimization techniques, within which the genetic type (GA) are widely used in the field of water distribution networks due to their versatility ((Savic & Walters, 1997) to explore and select optimal solutions in network dimensioning and management. These are inspired by the Darwinian principle of natural selection and genetic reproduction (Holland, 1992), and have also found applications in CIPN design (Farmani et al., 2007) and management (Fernández et al., 2017).
García et al. (2011) research specific CIPN design algorithms for shifts that perform a recursive extension of the Economic Series Method for shift-based systems, but in which the assignment of shifts to hydrants is pre-set. In Farmani et al. (2007), an GA is used to obtain a CIPN shift design, assigning both shifts and pipe diameters. When taking hydrant shifts and conduit diameters in the GA decision-making process into consideration, the dimensionality of the GA, and consequently its complexity as well as the calculation time, is unnecessarily increased.
For a given shift assignation, the problem of determining optimal diameters in the case of branched networks has analytical solutions. Therefore, the joint optimization of turns and diameters in CIPN in shifts can be advantageously carried out through the GA resource, limiting this only to the optimal shift allocation. This is a problem to which the GA seems especially adapted, while the dimensioning of a branched network can be developed more effectively with a subordinate analytical optimization process whose result must serve as an objective function. The integration of different optimization algorithms that exploit the best adaptation of different techniques to specific sub-problems in the area in which this research is framed.
Consequently, the main objective of this work is to develop and validate a hybrid algorithm that combines a genetic algorithm (GA) with an analytical algorithm based on Nonlinear Programming (NLP). The GA makes the optimal shift allocation to the hydrants while the NLP minimizes the costs of the network pipes, satisfying the pressure requirements of given shifts. In addition, an indicator is introduced that allows for the evaluation of the flexibility of the resulting designs to fit the shift changes that may occur during the network service. Finally, based on this flexibility indicator, a complementary criterion of decision support is proposed to select the most suitable design type in each case.
Formulation of the GA-NLP Hybrid Algorithm for the optimal design and the indicator of flexibility in shift networks
Algorithm and architecture of the hybrid model
a) Genetic Algorithm (GA)
Genetic algorithms were introduced by Holland (1992). The analogy of GA with nature lies in the creation of a set of solutions that are continuously evolving and self-perfecting. Thus, the set of evaluated solutions is called population, and each individual of this population represents a particular solution to the problem, composed of a group of values of each of the decision variables (genes), describing that particular solution. An individual will have greater chances of survival and reproduction the greater their aptitude or adaptation. That is, the better the value of their objective function. For each individual, the genes provide a numerical solution that is related on the one hand with their probability of survival and on the other with the probability of reproducing in the next generation. The processes of survival and reproduction are executed through genetic operators that are reproduction, crossing and mutation (Moradi-Jalal & Karney, 2008). Reproduction is the first stage, in which the best solutions of each chain that will endure in the process are determined. The crossover operator allows the exchange of information between different solutions to improve the value of the objective function until an optimal result is obtained (Savic & Walters, 1997). The number of chains that cross each other is known as crossing probability (P c ). The P c is greater the greater its aptitude, measured from the value of the objective function. Finally, the mutation operator guarantees the diversity of the solutions of each chain. Its objective is to increase the search areas within the space of feasible solutions to avoid converging to local optima. Mora-Melia, Iglesias, Martinez, and Fuertes-Miquel (2013) suggest taking as a value the probability of mutation (P m ) 1/N VD , with N VD being the number of decision variables (in this case the number of hydrants in the network, N h ). The values of P c and P m will be considered for the sensitivity analysis of the model.
The GA, due to its stochastic nature, do not guarantee the determination of the overall optimum result, although in many applications excellent results have been obtained (Savic & Walters, 1997; Boulos et al., 2001; Reis, Porto, & Chaudhry, 1997). The advantage of this type of algorithm lies in its generality, robustness and applicability to systems with multiple non-modeled interdependencies. For this reason, its use is frequent in solving complex problems of the Engineering Sciences, including the design of water distribution systems (Simpson, Dandy, & Murphy, 1994). In this research the GA is used exclusively to establish the allocation of shifts to the hydrants that assumes the minimum cost of the network, unlike the approximation of Farmani et al. (2007), who also carry out the assignment of diameters to pipes through GA.
The problem can be stated in the following way: There is a branch irrigation network with N h hydrants so that each hydrant corresponds to one irrigation shift. Each individual or solution is made up of several genes equal to the number of hydrant variables. That is, each gene represents a hydrant, and its genome collects the value corresponding to the shift assigned to it. Therefore, the problem has as many decision variables as hydrants, N VD = N h . Each gene will represent the shift assigned to hydrant j for the solution represented by individual i. These genes can take any value between 1 and the maximum number of shifts (N T ). Thus, an individual i in a population P can be represented as a vector:
The aptitude of an individual X i is identified through the value that the objective function adopts for said solution. In this case, the objective function is the minimum cost of the network corresponding to the allocation of shifts coded in the individual X i . Depending on the shifts assigned to each hydrant, the circulating flows are obtained for each pipeline in each shift. The sizing process based on NLP makes the design of the network at minimum cost corresponding to these flows. The sizing process is described below.
b) Non-Lineal Programming (NLP)
The set of restrictions of an irrigation system (pressure, flow, load loss) and its cost depend on the diameters of the pipes through non-linear relationships. Therefore, NLP can be applied to find optimal solutions that depend on diameters such as decision variables. There are several methods of NLP to solve problems in Engineering (Cortés-Martínez, Treviño-Cansino, Alcorta-García, Sáenz-López, & González-Barrios, 2015) focused on optimizing the design of the pipes, in the sense of minimizing system costs and satisfying certain restrictions. In this case, the Generalized Reduced Gradient (GRG) method was selected due to its effectiveness and precision (Lasdon, Fox, & Ratner, 1974). The GRG can be applied for both linear and non-linear functions.
The objective function to be minimized by NLP in the problem studied is the total cost of the pipes in the network, which depends on the diameters to be assigned to each section, and is described as follows:
In the equation (2),
The network configuration used in this research is branched, with only one type of material, a single nominal pipe pressure and a single power source (reservoir). The minimum pressure in each hydrant per shift is considered as a restriction, considering the number of shifts (t), the location of the power supply and its established piezometric height. Thus, for each shift t and each node n, this restriction can be presented as (equation 3):
In this equation,
The GRG method of NLP uses the diameters as continuous decision variables, whose optimal values do not correspond to standardized commercial diameters. Due to this, it is necessary to carry out a subsequent normalization process that modifies each optimal theoretical diameter resulting from the NLP to the nearest available diameter in the market (discrete diameters). Once this normalization process has been completed, the investment cost in the installation is reached.
c) Hybrid Algorithm (GA-NLP)
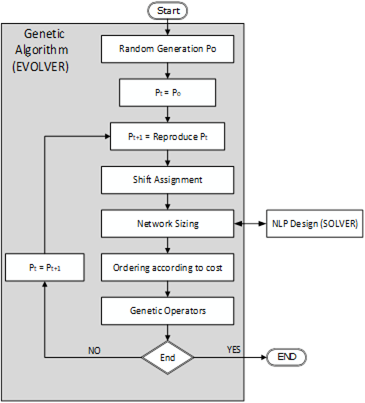
The Hybrid Algorithm, (GA-NLP), performs the design of a branched CIPN n operating with the shift mode, simultaneously optimizing the shifts assigned to each hydrant (using GA) and the dimensioning of the pipes of the network (through NLP). The objective is to minimize the system’s cost, exploiting in this way the best characteristics of each type of algorithm. Figure 1 shows the flow diagram of the GA-NLP method.
Through GA the shift belonging to each hydrant is found that minimizes the objective function, which is the cost of pipes in the network. In this way, the decision variables are exclusively the allocation of shifts to hydrants, and the dimensionality of the problem in the GA formulation is reduced. In each step of the GA, the tentative turns assigned to hydrants are evolved, using the cost of the network for the allocation of candidate shifts as an assessment of the aptitude of each individual. This process was implemented in the EVOLVER package (Palisade Corporation, 2010), which allows the incorporation of optimization processes through GA to conveniently codified problems of a general nature.
In turn, the cost of the network for an allocation of candidate shifts is the result of pipeline optimization using the GRG analytical algorithm with NLP. The function of the GRG algorithm is to calculate the pipeline distribution of continuous diameters in the network, which satisfies the pressure requirements and generates a minimum cost for a certain allocation of shifts to the hydrants. The GRG is incorporated in the SOLVER package (Frontline Systems Inc., 2011), a software package for general purpose simulation and optimization. In this work, a linkage of both algorithms has been made that allowed for the communication of results obtained by SOLVER for the network as values of the objective function used later by EVOLVER for the implementation of the GA, as shown in Figure 1, where P 0 represents the initial population and P t the resulting population for the process in the GA.
Once the final process solution is determined, with the diameters in each line, proceed to:
Normalize the theoretical diameters by the criterion of the nearest diameter
Check the resulting pressure values in each shift in all hydrants in the network with pressure restriction and readjust the diameter if necessary.
Check the flow velocity in all the network pipes and readjust if necessary.
Compute the cost of each pipe in the network according to the final standard diameter assigned.
Flexibility indicator of the CIPN to shifts
In the construction of the GA-NLP Hybrid Algorithm for the design of a CIPN, two criteria have been applied: (i) comply with the established pressure and (ii) minimize network costs with decision variables of both pipe diameter and the shift assignments. In the formulation of the objective function, no criteria of reliability or flexibility are introduced. However, in all shift networks, once they have been dimensioned, it is advisable to evaluate their capacity to continue providing adequate service in the event of shift change, a characteristic that will constitute their flexibility concerning shift changes. These changes frequently occur in the networks throughout their operation, and lead to the adoption of different combinations of hydrants assigned to a certain shift with respect to the initial assignment assumed in the design, respecting at least the total flow corresponding to the shift.
In Lamaddalena and Sagardoy (2000), for CIPN on demand, there is an antecedent that defines indicators that assess whether the level of pressure contributed to the hydrants is sufficient according to the number of open hydrants, with total flows below or above the design conditions. It is possible to extend these concepts to CIPN designed with shift operation to evaluate the flexibility of the same to fit changes of shifts.
The shift change is an unpredictable event with a large space of possibilities. Therefore, the preparation of indicators should explore scenarios that contemplate any shift reorganization with the condition that the total flow demanded in the shift is maintained, corresponding to a certain global percentage of open hydrants. Provided that the network has a sufficient number of hydrants with similar endowments, a change in shift configuration can be assimilated to a random opening of a percentage of hydrants equal to that corresponding to each initial shift.
For each shift assignment (random or deterministic), the pressure sufficiency condition in each hydrant (n) during a shift (t) means that the following relationship is satisfied (Lamaddalena & Sagardoy, 2000):
Where
The pressure compliance variable (
If there are a total of
The IFCT is a synthetic indicator that cushions possible pressure shortfalls in shift changes located in a few hydrants. If its value is high, (close to 1), it follows that all hydrants in the system maintain sufficient pressure before any shift change, indicating high CIPN flexibility. If the index is low (close to 0), the inability to supply sufficient pressure outside the design turn is frequent and affects many hydrants in the CIPN (low flexibility).
Procedure for Hybrid Algorithm Validation (GA-NLP) and its application to CIPN design
To verify the correct implementation of GA-NLP, investigate the services it provides, and evaluate the cost vs. flexibility of the designed systems, a systematic methodology has been developed that is summarized in the following steps.
Calibration of the parameters that influence GA solutions.
Comparison of the results with other design algorithms of shift-based networks in a set of four real CIPN, constituted as case studies.
Analysis of the flexibility of the designs found.
Sensitivity analysis for GA parameters
For this study, values of between 50 and 200 individuals for the set of selected networks have been taken as population sizes. Also, a crossing probability (P c ) of 0.5 (Mora, 2012) has been set as a reference value for the crossing operator. On the other hand, Mora-Melia et al. (2013) proposed to determine the probability of mutation (P m ) based on the number of the problem’s decision variables. These authors proposed to take the inverse, that is, 1/N h and define the space of feasible solutions to reduce the search time. Values close to 0.01 indicate that the process uses a large space to generate the optimal solution, while values close to 1 limit the search. The number of hydrants is different in each of the study networks, and this criterion will be used as a reference value. Thus, to adjust the GA, population values of 50, 100 and 200 individuals have been tested; crossing probabilities of 0.1 and 0.5, and P m values between 1/N VD and 0.9.
Comparison of results with alternative algorithms
To evaluate the effectiveness of the Hybrid Algorithm (GA-NLP), in terms of the cost of the designs produced, the total costs obtained in the optimal design process of a set of networks were compared using GA-NLP as well as three other alternative design methods.
The three alternative methods used variants of an algorithm based on the use of Lagrange Multipliers, (known in network design literature as Economic Series, MSEM). This method was improved for CIPN on demand (González & Aliod, 2003) and later extended for CIPN to shifts (García et al., 2011). This algorithm is implemented in the GESTAR 2016 software. GESTAR 2016 is an integrated package specifically for CIPN design and analysis. It is widely used in the projection and management of CIPN and used in literature to compare the costs of shift and demand-based designs and (Alduán & Monserrat, 2009; Monserrat et al., 2012). One of the modules of this GESTAR application was also used to facilitate the computation of FP n indices in the hydrants needed for IFCT calculation.
Since the GA-NLP hybrid method obtains continuous diameters which must be normalized at the end of the process, both results are incorporated into this work. The nomenclature and description of the compared design alternatives are listed below:
Method 1 (GA-NLP, continuous diameters): Assignment of optimal shifts through GA and network design using NLP, without diameter adjustment.
Method 2 (GA-NLP, normalized diameters): Method 1 plus diameter normalization, by automatic assignment to closer diameters and revision for the verification of minimum pressures and maximum speeds.
Method 3 (MSEM): Optimal shift sizing, through MSEM integrated in the GESTAR tool, with shift allocation obtained the Methods 1 and 2.
Method 4 (MSEM-tur-aleat): Optimal shift sizing, through MSEM integrated in the GESTAR tool, with random manual shift assignments (without optimization).
Method 5: Network design operating on-demand through MSEM integrated in the GESTAR tool, with total irrigation time equal to the sum of shift times.
Case studies
For the present study, four irrigation networks were selected, two located in Ecuador (San Rafael and Tuncarta) and 2 in Spain (Lower Callén and Valcuerna). Table 1 shows the number of hydrants, the irrigation surface, head reservoir surface elevation, setpoint pressures, continuous assumed flow rate, and the effective watering day of the four selected networks.
Table 1 Input data of studied networks.
| San Rafael | Tuncarta | Lower Callén | Valcuerna | |
|---|---|---|---|---|
| Number of hydrants | 48 | 84 | 51 | 67 |
| Irrigation surface (ha) | 84.42 | 93.56 | 628.30 | 585.65 |
| Cota reservoir free surface (mca) | 3 093.00 | 1 540.00 | 437.50 | 399.00 |
| Setpoint Pressure (mca) | 40 | 40 | 45-65 | 40 |
| Continuous assumed flow (L/s ha) | 0.30 | 0.35 | 0.80 | 0.82 |
| Effective Watering Day (h) | 17.49 | 23.82 | 23.52 | 23.62 |
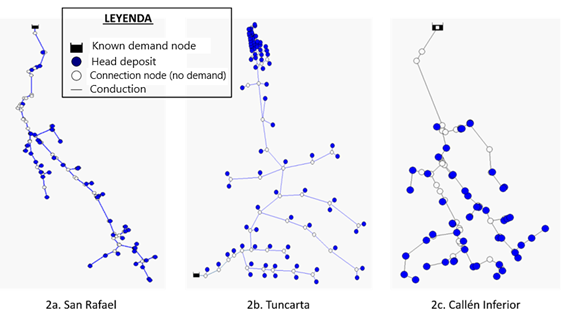
Figure 2 and Figure 3 show the topology of the different study networks. In these figures, the header node corresponding to the reservoir (node 0), the junction nodes in the network mainline, the demand nodes (hydrants), and the pipelines have been represented.
A summary of the characteristics of design shifts for 4 CIPN under study is presented in Table 2, which includes the time of shift duration and the head flow for each shift.
Table 2 Main characteristics of study networks.
| Network | Hydrant # | Shift # | Shift 1 | Shift 2 | Shift 3 | |||
|---|---|---|---|---|---|---|---|---|
| Irrigation Time (Hours) | Flow (L/s) | Irrigation Time (Hours) | Flow (L/s) | Irrigation Time (Hours) | Flow (L/s) | |||
| San Rafael | 48 | 3 | 5.83 | 31 | 5.83 | 35 | 5.83 | 38 |
| Tuncarta | 84 | 3 | 7.94 | 37 | 7.94 | 40 | 7.94 | 40 |
| Lower Callén | 51 | 2 | 11.76 | 771 | 11.76 | 684 | ||
| Valcuerna | 67 | 2 | 11.81 | 808 | 11.81 | 757 | ||
Results and discussion
Sensitivity analysis and parameter calibration of the GA-NLP Hybrid Algorithm
The results of the design costs obtained by the Hybrid Algorithm GA-NLP for each of the Case Studies considered is shown in Table 3, based on two sets of GA configuration parameters according to what is stated in Section “Sensitivity analysis for GA parameters”. In the first set of parameters, called Uniform Parameters, the parameter configuration of the crossover probability (P c ), mutation probability (P m ) and population size is initially assigned by default and uniformly for all cases, with values of 0.1, 0.9 and 200, respectively. The second set, denoted as Calibrated Parameters corresponds to a combination of parameters calibrated so that, in each case, it leads to the minimum cost, also reducing calculation times, both configurations being found in the extreme ranges of P m . The computer used has a Core i7 processor at 3.40 GHz with a RAM of 16 Gb. Table 3 includes the execution time of the algorithm, number of tests or executions, the total network design cost directly obtained by the GA-NLP with continuous pipe diameters (Method 1) and the total design cost once the diameters are normalized according to the procedure described in section “Comparison of results with alternative algorithms” (Method 2).
Table 3 Calibration results of genetic operators, study networks.
| Pc (%) | Pm (%) | Population Size | Execution Time (hours) | Number of Trials | Continuous Diameter Costs (USD) | Normalized Diameter Costs (USD) | |||
|---|---|---|---|---|---|---|---|---|---|
| San Rafael | Uniform Param. | 0.1 | 0.900 | 200 | 11.20 | 1154 | 98755.75 | 132257.19 | |
| Calibrated Param. | 0.5 | 0.021 | 50 | 0.45 | 104 | 88778.01 | 137722.00 | ||
| Tuncarta | Uniform Param. | 0.1 | 0.900 | 200 | 14.10 | 1463 | 21114.63 | 27387.44 | |
| Calibrated Param. | 0.5 | 0.012 | 50 | 5.00 | 2079 | 20614.93 | 27489.99 | ||
| Lower Callén | Uniform Param. | 0.1 | 0.900 | 200 | 8.45 | 947 | 1717194.71 | 1876238.34 | |
| Calibrated Param. | 0.5 | 0.020 | 50 | 3.17 | 1001 | 1461169.30 | 1747343.00 | ||
| Valcuerna | Uniform Param. | 0.1 | 0.900 | 200 | 9.55 | 1970 | 5718114.75 | 7111668.49 | |
| Calibrated Param. | 0.5 | 0.015 | 50 | 4.42 | 2735 | 5416379.63 | 6981602.00 | ||
As can be seen, the differences in design cost with normalized diameters for the Case Studies, using values of uniform initial crossover and mutation operators, or calibrated parameters for each case, which suppose even extreme values, is small. However, the calculation time is significantly reduced when the parameters are calibrated, due to the associated population size (Table 3). Based on those mentioned above, for the following analyses and comparisons, the results obtained shall be adopted with uniform parameters, not calibrated "ad hoc" for each case, since they represent the most unfavorable condition. These results demonstrate the robustness and consistency of the GA-NLP Hybrid Algorithm presented to find viable solutions when applied to Case Studies of diversified characteristics even with very different Pc and Pm parameters, without needing to force the "ad hoc" introduction of perturbations in the mutation process as in Farmani et al. (2007) by the high dimensionality of the decision variables involved in the same GA both for the allocation of shifts and diameters.
Comparison of costs and flexibility of the GA-NLP Hybrid Algorithm designs and alternative design methods
The results, in terms of network pipe cost of the optimal designs of the Case Studies for all the Design Methods described in Section 3.2 are presented in Table 4. The IFCT value of the designed networks is also included with each one of said methods.
Table 4 Cost values and IFCT for the Case Study networks according to the Design Method.
| Case Study | Method 1 | Method 2 | Method 3 | Method 4 | Method 5 | |
|---|---|---|---|---|---|---|
| San Rafael | Cost, USD | 98755 | 132257 | 132976 | 146556 | 195698 |
| IFCT | 0.80 | 0.90 | 0.82 | 0.77 | 0.91 | |
| Tuncarta | Cost, USD | 21114 | 27387 | 27191 | 28274 | 34012 |
| IFCT | 0.77 | 1 | 0.88 | 0.86 | 0.99 | |
| Lower Callén | Cost, USD | 1717194 | 1876238 | 1900494 | 1925878 | 2461679 |
| IFCT | 0.88 | 0.81 | 0.81 | 0.80 | 0.99 | |
| Valcuerna | Cost, USD | 5718114 | 7111668 | 6885207 | 8370887 | 6883102 |
| IFCT | 0.91 | 0.94 | 0.93 | 0.92 | 0.97 | |
It is observed in Table 4, that even without considering Method 1, a direct result of applying the GA-NLP before the normalization of the diameters, said algorithm with subsequent normalization (Method 2) always obtains a lower cost than the design procedure for shifts optimized by traditional Economic Series-type analytical algorithms, with shifts assigned in a heuristic way (Method 4). When comparing the results of the cost of the networks by means of Method 2, with Method 3, in which shift allocation has been introduced by means of GA-NLP (Method 1 and 2) are similar values. This suggests the decisive influence of shifts allocation in cost reduction in networks designed to operate shifts, apparently this GA-NLP capacity being more relevant than the algorithm itself used in the dimensioning of the pipelines.
Once the effectiveness of the GA-NLP Hybrid Algorithm has been proven to generate cheaper shift-network designs than those found by traditional alternative methods, the flexibility achieved can be analyzed with the GA-NLP (Method 2) concerning the alternative design methods presented in this study. Table 5 shows the percentage variations of pipeline costs and the IFCT of Methods 3, 4 and 5 (M3, M4, M5 respectively in said Table) with respect to Method 2, which is taken as reference in all the variants. The percentages of positive cost increases (Δ Cost %) and negative IFTC increments (Δ IFCT %) imply higher price and less flexibility, respectively, of the alternative indicated with respect to the GA-NLP results (M2).
Table 5 Relative cost variations and IFCT for the case studies.
| (M3-M2)/M2 % | (M4-M2)/M2 % | (M5-M2)/M2 % | ||||
|---|---|---|---|---|---|---|
| CASE | Δ IFCT (%) | Δ Cost (%) | Δ IFCT (%) | Δ Cost (%) | Δ IFCT (%) | Δ Cost (%) |
| SAN RAFAEL | -8.97 | 0.54 | -13.94 | 10.81 | 1.42 | 47.97 |
| TUNCARTA | -11.97 | -0.72 | -13.71 | 3.24 | -0.41 | 24.19 |
| LOWER CALLÉN | 0.93 | 1.29 | -0.35 | 2.65 | 22.66 | 31.20 |
| VALCUERNA | -1.48 | -3.18 | -2.01 | 17.71 | 3.33 | -3.21 |
In Figure 4 (a, b), the percentage increases of cost (Δ Cost %) are correlated with the respective IFCT increase (Δ IFCT%) for Methods 3 and 4.
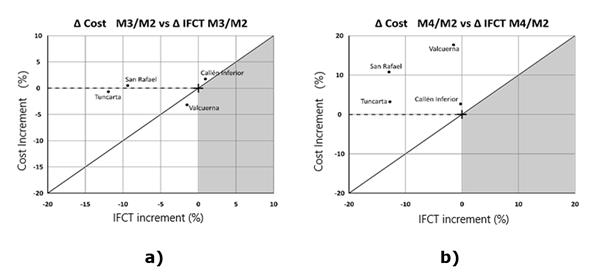
Figure 4 a) Relative cost variations vs. relative IFTC variations M3/M2 for the Case Studies; b) Relative cost variations vs. relative IFTC variations M4/M2 for the case studies.
From the comparison between Method 3 (which has required information from the optimal shifts obtained from Method 2) and Method 2, it is observed in Table 5 (first column) and Figure 4a, that in the CIPN shift designs with Method 3, the costs are similar to Method 2 with more flexible designs. With Method 3, the network flexibility decreases by a total average of -5.37%, except the Lower Callén network, where flexibility increased slightly (0.92%).
Method 4 not only generates more expensive designs, but is also less flexible than Method 2, (see Table 5, column 2, and Figure 4b). There is an increasing trend in total network costs (average: 8.6%) and a reduction in flexibility (average: -7.50%). The reason is the lack of shift optimization involving Method 4, which again highlights the great importance of the shift allocation in the design concept.
All of this indicates that the GA-NLP Algorithm generates designs with not only cheaper results than the alternative design procedures for shuffled shifts, but also more flexibility in the face of overtime shift changes.
Shift design vs. demand design
As a collateral result, in the light of the previous analyses, a criterion has been inferred to help with rational decision-making when establishing the convenience of a shift-based or demand-based design of a new CIPN. This criterion consists of relating the design costs and flexibility to shifts (Method 2) with that of design to demand (Method 5).
With the data in Table 5, Column 3, Figure 5 is drawn. The abscissa axis represents the percentage of the IFCT increase from design to demand (Method 5) with respect to the shift design (Method 2). The ordinate axis indicates the cost-percentage increase of the design to the demand (Method 5) with respect to the design in shifts (Method 2). The diagonal line indicates the region where the increase in costs increases in a similar way to the increase in flexibility.
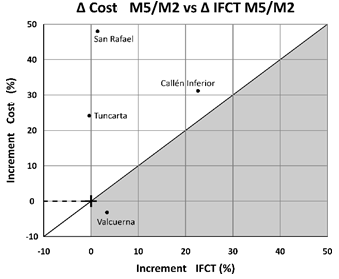
Figure 5 Relative cost variations vs. relative IFCT variations when moving to a demand design (M5) from a shift design (M2) for the case studies.
In cases where the cost increases versus the flexibility increases (IFCT) are located above-said line, the shift-based design will be the most appropriate, since the design’s cost increases to the demand with respect to the shift design exceed the corresponding flexibility increases. The cases that located next to or below said line (shaded area of Figure 5) would point to a preference of demand design. These conditions can be formalized stating that the demand design would be recommended if:
Otherwise, it will be more advisable to form a shift design. This criterion cannot be taken in an absolute but in an indicative way, and it must be complemented with other important parameters in the decision-making, as presented in Espinosa et al. (2016).
When applying this criterion to the 4 case studies, it is evident that in the Tuncarta and San Rafael networks the cost increases remarkably (average: 36%) without improving the flexibility, and in Figure 5 they are clearly above the shaded area. For these networks it is advisable to carry out the design with the shift modality. For the Lower Callén network, both the IFCP and the cost increased 20% and 30% respectively, reaching the threshold of the convenience of the demand design. Therefore, in such networks it might be advisable to design a network operating on demand to obtain better advantages in operating the system, considering the available resources. For the Valcuerna case, demand design cost less than the shift-based design. This is because hydrant opening times are very different and, consequently, demand-design flows are lower than those in shift-design. For this reason, the best option is the demand-design, unless both the number of shifts and their duration are redefined, and the provisions to homogenize the opening times of the hydrants are be modified.
There is a high variability of cost differences between demand and shift designs according to each case study’s network, with savings in shift design versus demand design located between 19% and 32%. These variations are in line with what has been observed in other investigations focused on establishing comparisons between demand and shift designs. In the network studied in Espinosa et al. (2016), the savings in the shift system versus the demand system is 22%. In the network analyzed by Alduán and Monserrat (2009), this saving is 15%, and in the three cases found in Monserrat et al. (2012) is in a range of 5% to 9%. The fact that this research has found generally greater savings is interpreted to be due to the fact that we have optimized the allocation of shifts, as is also the case presented in Farmani et al. (2007) in which savings amounted to 55%.
Conclusion
A Hybrid Algorithm (GA-NLP) has been presented that is proven to be robust and efficient to obtain minimum-cost CIPN designs where the decision variables simultaneously optimized are the allocation of shifts to the hydrants and the diameter variable to each section of pipe. The calibration of the parameters controlling the evolution of the GA involved has concluded that the calculation time required is sensitive to them, but the minimum costs encountered are not so much. The algorithm and its features have been validated through the application to four real Case Studies. The results have been compared with alternative optimal CIPN design procedures, based on Economic Series-type algorithms, which are executed in very short times, finding that the GA-NLP Hybrid Algorithm, although it requires much more calculation time, generates lower-cost designs, and that said savings is largely due to the optimization of shifts that it provides.
A parameter indicating a CIPN’s flexibility with respect to shifts, IFCT, has also been introduced, which has been used to evaluate the adaptability of the designs found in response to subsequent changes in the configuration of shifts. It is concluded that the GA-NLP Hybrid Algorithm produces cheaper, more flexible designs than the alternative shift-based design methods with which they have been compared.
Finally, the correlation of the IFCT indicator variations with the changes in network cost value, when moving from a shifts design to a demand design, has permitted the formulation of a complementary rational criterion to help the decision on the most convenient CIPN design type, demand or shift.
Acknowledgments
We thank the Private Technical University of Loja for the sponsorship given for the development of this research, Dr. Andreas Fries and Eng. José María Ciria, for their collaboration.
REFERENCES
Alduán, A., & Monserrat, J. (2009). Estudio comparativo entre la organización a la demanda o por turnos en redes de riego a presión. Ingeniería del Agua, 16(3), 235-244. Recuperado de https://polipapers.upv.es/index.php/IA/article/view/2951/2954 [ Links ]
Boulos, P. F., Wu, Z., Orr, C. H., Moore, M., Hsiung, P., & Thomas, D. (2001). Optimal pump operation of water distribution systems using genetic algorithms. Distribution System Symposium. American Water Works Association (AWWA). Denver, Co., USA. Recuperado de https://www.semanticscholar.org/paper/Optimal-Pump-Operation-of-Water-Distribution-Using-Boulos- Wu/30bd0b8898b9c7eede6581df60fe8aaf2964d0f7 [ Links ]
Clément, R. (1966). Calcul des débits dans les réseaux d’irrigation fonctionnant à la demande. La Houille Blanche, (5), 553-576, DOI: 10.1051/lhb/1966034. [ Links ]
Cortés-Martínez, F., Treviño-Cansino, A., Alcorta-García, M. A., Sáenz-López, A., & González-Barrios, J. L. (2015). Optimización en el diseño de lagunas de estabilización con programación no lineal. Tecnología y ciencias del agua, 6(2), 85-100. Recuperado de http://www.scielo.org.mx/pdf/tca/v6n2/v6n2a6.pdf [ Links ]
Espinosa, E., Flores, M., Hernández, R.A., & Carrillo, F. (2016). Análisis técnico y económico del diseño de un sistema de riego a hidrante parcelario utilizando el método por turnos y la técnica de Clement. Terra Latinoamericana, 34(4), 431-440. Recuperado de http://www.scielo.org.mx/pdf/tl/v34n4/2395-8030-tl-34-04-00431.pdf [ Links ]
Deb, A. K. (1974). Least cost design of branched pipe network system. Journal of the Environmental Engineering Division, 100(4), 821-835 Recuperado de http://cedb.asce.org/CEDBsearch/record.jsp?dockey=0021690 [ Links ]
Faci, E., García, S., Aliod, R., Paño, J., Seral, P., & García, A. (octubre, 2015). Algortimos y herramientas para la aplicación de estrategias de reducción de costes energéticos en sistemas de riego a presión. J. En: Roldán-Cañas, J. (presidencia). La precipitación y los procesos erosivos . Simposio llevado a cabo en las IV Jornadas de Ingeniería del Agua. Organiza: Fundación para el Fomento de la Ingeniería del Agua, Córdoba, España, 21-22 de octubre de 2015. Recuperado de http://www.uco.es/jia2015/ponencias/b/b022.pdf [ Links ]
Farmani, R., Abadia, R., & Savic, D. (2007). Optimum design and management of pressurized branched irrigation networks. Journal of Irrigation and Drainage Engineering, 133(6), 528-537, DOI: 10.1061/(ASCE)0733-9437(2007)133:6(528) [ Links ]
Fernández, I., Montesinos, P., Camacho, E., & Rodríguez, J. A. (2017). Optimal design of pressurized irrigation networks to minimize the operational cost under different management scenarios. Water Resources Management, 31(6), 1995-2010, DOI: 10.1007/s11269-017-1629-2 [ Links ]
Frontline Systems Inc. (2011). Frontline Solvers User Guide for Use with Excel 2003-2010 (Versión 11.5). Recuperado de https://www.solver.com/files/_document/FrontlineSolvers_UserGuideV11.pdf [ Links ]
García, S., Ruiz, R., Aliod, R., Paño, J., Seral, P., & Faci, E. (junio, 2011). Nuevas herramientas implementadas en GESTAR 2010 para el dimensionado de tuberías principales en redes de distribución en parcela y redes de distribución general a turnos. En: Berbel-Vecino, J. (presidencia). Hacia un regadío eficiente y rentable . Simposio llevado a cabo en el XXIX Congreso Nacional de Riegos. Organiza: Agencia Española de Riegos y Drenajes Córdoba, España, 7-9 de junio de 2011. Recuperado de Recuperado de http://www.aeryd.es/escaparate/gmms/aeryd/buscadortrabajos?accion=ver&id=7355 [ Links ]
González, C., & Aliod, R. (mayo, 2003). Mejoras en el método de la serie económica para el dimensionado de redes ramificadas. En: Vélez-Sánchez, A. (presidencia). Ingeniería del riego . Simposio llevado a cabo en el XXI Congreso Nacional de Riegos. Organiza: Agencia Española de Riegos y Drenajes Mérida, España, 6-8 de mayo de 2003. Recuperado de http://www.aeryd.es/escaparate/gmms/aeryd/buscadortrabajos?accion=ver&id=6715 [ Links ]
Holland, J. H. (1992). Genetic Algorithms. Scientific American, 267(1), 66-72, DOI: 10.1038/scientificamerican0792-66 [ Links ]
Jiménez, M. A., Martínez, F., Bou, V., & Bartolí, H. J. (2010). Methodology for grouping intakes of pressurized irrigation networks into sectors to minimize energy consumption. Biosystems Engineering, 105(4), 429-438, DOI: 10.1016/j.biosystemseng.2009.12.014 [ Links ]
Kale, R. V., Singh, R. P., & Mahar, P. S. (2008). Optimal design of pressurized irrigation subunit. Journal of Irrigation and Drainage Engineering , 134(2), 137-146, DOI: 10.1061/(ASCE)0733-9437(2008)134:2(137) [ Links ]
Labye, Y. (1966). Etude des procedes de calcul ayant pour but de rendre minimal le cout d´un reseau de distribution déau sous pression. La Houille Blanche , (5), 577-583, DOI: 10.1051/lhb/1966035 [ Links ]
Lamaddalena, N., Khadra, R., & Tlili, Y. (2012). Reliability-based pipe size computation of on-demand irrigation systems. Water Resources Management, 26(2), 307-328. DOI: 10.1007/s11269-011-9919-6 [ Links ]
Lamaddalena, N., & Sagardoy, J. (2000). Performance analysis of on-demand pressurized irrigation systems. Roma, Italia: Organización de las Naciones Unidas para la Alimentación y la Agricultura, FAO. Recuperado de https://books.google.com.ec/books?hl=es&lr=&id=TWFaiibeFFUC&oi=fnd&pg=PA1&ots=8Ck9thVE8i&sig=fsV4wuAlAAXMNtdI_jcbos-ALSc#v=onepage&q&f=false [ Links ]
Lasdon, L. S., Fox, R. L., & Ratner, M. W. (1974). Nonlinear optimization using the generalized reduced gradient method. Revue Française d’Automatique, Informatique, Recherche Opérationnelle, 3, 73-103. Recuperado de http://www.numdam.org/item?id=RO_1974__8_3_73_0 [ Links ]
Monserrat, J., Alduán, A., Cots, L., & Barragán, J. (septiembre, 2012). ¿Turnos o demanda? En el proyecto de redes de distribución de riego a presión. XV Congreso Latinoamericano de Hidráulica. Organiza: IAHR Latin-American Division, San José, Costa Rica, 9-12 de septiembre de 2012. Recuperado de https://repositori.udl.cat/bitstream/handle/10459.1/45935/Comparaci%F3n?sequence=1 [ Links ]
Mora, D. (2012). Diseño de redes de distribución de agua mediante algoritmos evolutivos. Análisis de eficiencia (tesis doctoral). Universidad Politécnica de Valencia, Valencia, España. Recuperado de http://hdl.handle.net/10251/16803 [ Links ]
Mora-Melia, D., Iglesias, P. L., Martínez, F. J., & Fuertes-Miquel, V. S. (2013). Design of water distribution networks using a pseudo-genetic algorithm and sensitivity of genetic operators. Water Resources Management, 27(12), 4149-4162, DOI: 10.1007/s11269-013-0400-6 [ Links ]
Moradi-Jalal, M., & Karney, B. W. (2008). Optimal design and operation of irrigation pumping stations using mathematical programming and Genetic Algorithm (GA). Journal of Hydraulic Research, 46(2), 237-246, DOI: 10.1080/00221686.2008.9521858 [ Links ]
Palisade Corporation. (2010). Guía para el uso de Evolver. Solver de algoritmo genético para Microsoft Excel (Versión 5.7). Recuperado de http://www.palisade.com/downloads/manuals/ES/Evolver5_es.pdf [ Links ]
Pérez, R., Martínez, F., & Vela, A. (1993). Improved design of branched networks bely using pressure‐reducing valves. Journal of Hydraulic Engineering, 119(2), 164-180, DOI: 10.1061/(ASCE)0733-9429(1993)119:2(164) [ Links ]
Planells, P., Ortega, J. F., Valiente, M., Montero, J., & Tarjuelo, J. M. (1999). Criterios para el diseño de redes colectivas de riego. Ingeniería del Agua, 6(1), 27-36, DOI: 10.4995/ia.1999.2773 [ Links ]
Reis, L. F. R., Porto, R. M., & Chaudhry, F. H. (1997). Optimal location of control valves in pipe networks by genetic algorithm. Journal of Water Resources Planning and Management, 123(6), 317-326, DOI: 10.1061/(ASCE)0733-9496(1997)123:6(317) [ Links ]
Salazar-Moreno, R., Rojano-Aguilar, A., & López-Cruz, I. L. (2014). La eficiencia en el uso del agua en la agricultura controlada. Tecnología y ciencias del agua, 5(2), 177-183. Recuperado de http://www.scielo.org.mx/pdf/tca/v5n2/v5n2a12.pdf [ Links ]
Savic, A., & Walters, A. (1997). Genetic algorithms for least-cost design of water distribution networks. Journal of Water Resources Planning and Management, 123(2), 67-77, DOI: 10.1061/(ASCE)0733-9496(1997)123:2(67) [ Links ]
Simpson, A. R., Dandy, G. C., & Murphy, L. J. (1994). Genetic algorithms compared to other techniques for pipe optimization. Journal of Water Resources Planning and Management, 120(4), 423-443, DOI: 10.1061/(ASCE)0733-9496(1994)120:4(423) [ Links ]
Theocharis, E., Tzimopoulos, D., Yannopoulos, I., & Sakellariou, M. (2006). Design of optimal irrigation networks. Irrigation and Drainage, 55, 21-32, DOI: 10.1002/ird.214 [ Links ]
Received: August 22, 2018; Accepted: March 20, 2019











 text in
text in