Services on Demand
Journal
Article
Indicators
Related links
Share
Tecnología y ciencias del agua
On-line version ISSN 2007-2422
Tecnol. cienc. agua vol.10 n.6 Jiutepec Nov./Dec. 2019 Epub May 15, 2020
https://doi.org/10.24850/j-tyca-2019-06-03
Articles
Non-stationary frequency analysis by linear regression and LN31, LP31 y GVE1 distributions
1 Profesor jubilado de la Universidad Autónoma de San Luis Potosí, México, campos_aranda@hotmail.com
All hydraulic works required by society are planned and dimensioned based on Floods Design. The most reliable estimation is made through frequency analysis (FA), consisting of fitting a probability distribution function (PDF) to the available data of annual maximum flows, in order to obtain the predictions sought. The FDP Log-Normal of three parameters of fit (LN3) was the first one of extensive application in the hydrological analyzes; the other two used have been established under precept for the FA of floods; the Log-Pearson type III (LP3) in U.S.A. and the General of Extreme Values (GVE) in England. The effects of climate change and the physical alterations of the basins, due to urbanization and deforestation, originate ascending tendencies in the flood registers; on the other hand, the construction of reservoirs leads to descending tendencies. Because of the above, the aforementioned data is non-stationary and its FA requires PDF to change over time, as a covariate. When the location parameter and the mean vary with time, in the quantile function of the LN3 distribution, its non-stationary model called LN31 is obtained. If the mean and the variance change over time, in the quantile function of the probabilistic model LP3, its non-stationary version designated LP31 is developed. Instead, when the fit parameters of the GVE model change over time, its non-stationary version called GVE1 is obtained. In this study, two records with ascending tendencies are processed, one of 77 annual maximum flows and the other of 58 annual maximum daily precipitation values. The results are analyzed and a selection of predictions is based on the lowest standard error of fit. Conclusions regarding the FA of series of extreme hydrological data with tendency highlight the simplicity of the method exposed, through the LN31, LP31 and GVE1 models.
Keywords Non-stationary hydrological data; bivariate linear regression; conditional moments; Log-Normal distribution; Log-Pearson type III distribution; General Extreme Value distribution; standard error of fit
Todas las obras hidráulicas que requiere la sociedad se planean y dimensionan con base en las crecientes de diseño. Su estimación más confiable se realiza a través del análisis de frecuencias (AF), que consiste en ajustar una función de distribución de probabilidades (FDP) a los datos disponibles de gastos máximos anuales, para obtener las predicciones buscadas. La FDP Log-Normal de tres parámetros de ajuste (LN3) fue la primera de aplicación extensa en los análisis hidrológicos; las otras dos utilizadas han sido establecidas bajo precepto para los AF de crecientes, la Log-Pearson tipo III (LP3) en EUA y la General de Valores Extremos (GVE) en Inglaterra. Por otra parte, los efectos del cambio climático y las alteraciones físicas de las cuencas por urbanización y deforestación originan en los registros crecientes tendencias ascendentes; en cambio, la construcción de embalses genera tendencias descendentes. Debido a lo anterior, los datos citados son no estacionarios y su AF requiere de FDP que vayan cambiando con el tiempo, como covariable. Cuando el parámetro de ubicación y la media varían con el tiempo, en la función de cuantiles de la distribución LN3, se obtiene su modelo no estacionario, denominado LN31. Si la media y la varianza cambian con el tiempo, en la función de cuantiles del modelo probabilístico LP3, se desarrolla su versión no estacionaria designada LP31. En cambio, cuando los parámetros de ajuste del modelo GVE cambian con el tiempo se obtiene su versión no estacionaria, denominada GVE1. En este estudio se procesan dos registros con tendencia ascendente: uno de 77 gastos máximos anuales y otro de 58 valores de precipitación máxima diaria anuales. Se analizan los resultados y la selección de predicciones se basa en el menor error estándar de ajuste. Las conclusiones destacan la sencillez del método expuesto en el AF de series de datos hidrológicos extremos con tendencia, a través de los modelos LN31, LP31 y GVE1.
Palabras clave datos hidrológicos no estacionarios; regresión lineal bivariada; momentos condicionales; distribución Log-Normal; distribución Log-Pearson tipo III; distribución General de Valores Extremos; error estándar de ajuste
Introduction
Generalities
The hydrological design in the stages of planning, construction, operation and revision of hydraulic works, is based on the so-called Flood Design (CD, for its Spanish initials). That is in the case of reservoirs, protective levees, canals, bridges and/or urban drainage structures. CDs are maximum river flows associated with low probabilities of exceedance, whose most reliable estimate is made by means of the Flood Frequency Analysis (AFC), when hydrometric data of maximum annual flows are available.
The AFC is a probabilistic procedure consisting of the following five steps: (1) verification of the statistical quality of the data or available sample; (2) selection of a probability distribution function (FDP), or probabilistic model from which the data is likely to come, (3) estimation of the FDP fitting parameters; (4) calculation of predictions or values associated with a certain probability of non-exceedance, it is made based on the FDP tested and (5) selection of results, in an objective way, the best fit achieved with each FDP and method of estimating its parameters is sought (Kite, 1977; Stedinger, Vogel, & Foufoula-Georgiou, 1993; Rao & Hamed, 2000; Meylan, Favre & Musy, 2012; Salas, Obeysekera & Vogel, 2018).
When there are no hydrometric data, the estimation of the CD is addressed through the so-called hydrological methods, which transform design hietograms into hydrographs or peak flow sought (Majumdar & Kumar, 2012). Estimation of the design storms is based on the curves Intensity-Duration-Frequency, but due to the scarcity of pluviographic or rain-gauge records, it is usually done through the probabilistic analysis of rainfall records of maximum daily precipitation (PMD). These records are usually wider and have much higher spatial coverage (Teegavarapu, 2012; Johnson & Sharma, 2017).
The AFC is identical to the probabilistic analysis of PMD records and therefore, the first step of both procedures is to verify that the annual data samples of maximum flows or PMD have been generated by a stationary random process, that is, that has not changed over time. This means that the record to be processed must not have deterministic components such as trend, persistence, or abrupt changes in the mean.
Unfortunately, the effects of global or regional climate change and the physical alterations suffered by the drainage basins or the surroundings of rain-gauge stations give rise to records of floods and of PMD that are nonstationary because they show trends. In general, the upward trends in the samples of floods are a consequence of urbanization or deforestation and the downward ones of the construction of reservoirs of use and/or control. In the series of annual PMD trends are commonly associated with the effects of regional climate change (Nguyen, El Outayek, Lim & Nguyen, 2017; Serago & Vogel, 2018; Salas et al., 2018).
Khaliq, Ouarda, Ondo, Gachon and Bobée (2006) concisely describe the various existing approaches to carry out the processing of non-stationary records. On the other hand, El Adlouni, Ouarda, Zhang, Roy and Bobée (2007) expose a specific procedure based on the fitting of the Generalized Extreme Values (GVE) distribution by means of the generalized maximum likelihood method and compare the stationary model (GVE0) with the non-stationary that accepts linear dependence in its location parameter (u) with a covariate or GVE1 model. When the dependence is quadratic or curve, the GVE2 model is defined and when there is a linear dependence also in the scale parameter (α) the GVE11 model is established. El Adlouni and Ouarda (2008) present the generalization of the L-moment method to the fitting of the non-stationary GVE1 and GVE2 distributions.
The previous approaches, as well as that of Aissaoui-Fqayeh, El Adlouni, Ouarda and St. Hilaire (2009), allow the use of a covariate different from time, for example, those associated with global climatic behavior. Campos-Aranda (2018) presents examples of the application of the GVE1 and GVE2 models, using the generalization of the L-moments method and as covariates the time and the Southern Oscillation Index (SOI).
Serago and Vogel (2018) suggest performing the probabilistic analysis of the non-stationary records, by means of a bivariate regression, which describes the relationship between the data (x) and the exogenous variable or covariate. Then they obtain the conditional mean, variance and asymmetry of x and y = ln (x), to apply them to the FDPs of three fitting parameters: Log-Normal (LN3), Log-Pearson type III (LP3) and stationary GVE and obtain their respective non-stationary models. The Log-Normal distribution was the first to reach a generalized application in the AFC, in the decade of the 1960s. LP3 and GVE functions were the first whose application was established under precept in the U.S.A. and England. GVE model became the classic distribution of the frequency analyses of hydrological extreme values and the LP3 function is the basic model of the AFC, therefore its non-stationary version (LP31), now developed by Serago and Vogel (2018), will certainly have great significance in the estimation of CDs, through records with trending.
Salas et al. (2018) indicate that Serenaldi and Kilsby (2015), among other authors, have recommended that stationarity always remain as an option to apply in the AFC. This is justified by the fact that the non-stationary condition detected may not be caused by physical causes of anthropogenic actions or climate change, but may have been caused by low-frequency components of the ocean-atmosphere system López-de-la-Cruz & Francés, 2014; Álvarez-Olguín & Escalante-Sandoval, 2016) or by the effects of persistence (Khaliq et al., 2006).
Objective
This study describes in detail the operating procedure of Serago and Vogel (2018), to apply the stationary LN3, LP3 and GVE distributions and the non-stationary distributions LN31, LP31 and GVE1 to records of floods and annual PMD showing linear trend. Two numerical applications are presented, the first to a record of 77 annual maximum flows and the second to a series of annual PMD with 58 data; both show an upward trend. The selection among the three FDPs is made based on the standard error of fit. The major contribution of this study is to describe and apply the non-stationary version of the LP3 distribution, applicable to records with trend, with a fairly simple method that corrects its quantile function.
Operative theory and data to be processed
Linear regression model
The general regression model, whose structure and theoretical properties will be analyzed and applied is (Serago & Vogel, 2018; Salas et al., 2018):
in which, x are the data of the series of annual extreme hydrological values (floods, winds, levels, precipitations, temperatures, etc.), f(·) is a transformation of x to make it linear, w 1 and w 2 are the covariates of the climate or the land use, β 1 and β 2 are the coefficients of the model and ε is the model error, which is considered independent, with uniform variance and with Normal distribution.
Vogel, Yaindl and Walter (2011) and Prosdocimi, Kjeldsen and Svensson (2014) have found that the previous model, when y = ln(x) and w 1 is considered the time (t) in years, it is useful to analyze trending floods in U.S.A. and U.K. rivers, regardless of whether the trend was significant or not. Serago and Vogel (2018) emphasize that such a simple model does not imply any hypothesis regarding the FDP of the variable y. Besides, they modify the linear regression to introduce the mean values (μ) of the variables, and then we have:
now, the variable y is conditioned by the explicative variable w, β is the coefficient of regression and ε is once again the error of the model with mean zero and variance constant and equal to:
where, ρ is the linear correlation coefficient between y and w. Considering that there are no missing values in the annual series of extreme hydrological values and that their size is n, then the estimates in Equation (2) are (Prosdocimi et al., 2014; Serago & Vogel, 2018):
whereby:
Applying Equations (6) and (7) to the original data x, their mean (ˉx) and standard deviation (σ x ) are defined. Their asymmetry coefficient is calculated with the expression:
Non-conditional moments
According to Serago and Vogel (2018), when performing a stationary frequency analysis, the moments of x and y = ln(x) do not depend on the explanatory variable w, therefore, they are non-conditional moments and are defined by their means (μ x , μ y ), standard deviations (σ x , σ y ) and asymmetry coefficients (γ x , γ y ).
Conditional moments of y
Serago y Vogel (2018) use Equation (2) to obtain the conditional moments that will be used in the non-stationary frequency analysis, without making any consideration about the FDP of the variable y. The mean of Equation (2) leads to the expression of the expected value of y conditioned by w, this is:
Similarly, the conditional variance of y is obtained using Equations (3) and (10), to obtain:
The above equation shows that the conditional variance of y decreases as the explanatory power of the trend increases, tending to zero when ρ approaches the unit. On the contrary, when p tends to zero the conditional variance tends to the original. In general, in the non-stationary frequencies analysis the conditional variance of y is lower than the non-conditional variance. Serago and Vogel (2018) find that the conditional asymmetry of y is:
The above expression indicates that the conditional asymmetry of y is equal to the non-conditional asymmetry, when the asymmetry of the explanatory variable (γ w ) is zero, case of w equal to time (t).
Conditional moments of x
Serago and Vogel (2018) apply the exponential function to Equation (2) and obtain the expression:
in which, x w and y w are the conditioned values by the explanatory variable w. Note that hypothesis regard the FDP of x w and y w have not been established; but according to Equation (15) it is probable that x w comes from a distribution Normal and that y w does it from a Log-Normal function. The above is valid because the only variable on the right side of Equation (15) is the error of model ε and exp(ε), which are approximately Normal and Log-Normal, respectively.
To obtain the expressions of the conditional moments of x, it will be accepted that x w approaches a Log-Normal distribution and then the equations that relate the mean, variance and asymmetry of x and of y =ln(x) are used in the Log-Normal distribution, which are (Serago & Vogel, 2018):
Finally, Equations (16) to (18) are extended by applying expressions (12) and (13), to obtain:
Stationary LN3 distribution
If a series of annual extreme hydrological values (y) defined as y = ln(x - a) follows a Normal distribution with mean and standard deviation equal to μ y and σ y , then the variable x has a Log-Normal distribution of three fitting parameters (LN3), being a its lower limit or location parameter. Predictions associated with a certain return period (Tr), which is the reciprocal of the exceedance probability, are estimated with the expressions (Kite, 1977; Rao & Hamed, 2000):
where:
being:
and:
In the above expression, γ x is calculated with Equation (11). Finally, Z in Equation (23) is the standardized normal variable; it is estimated based on the following algorithm (Zelen & Severo, 1972) for a non-exceedance probability (p):
with
c 0 = 2.515517c 1 = 0.802853c 2 = 0.010328
d 1 = 1.432788d 2 = 0.189269d 3 = 0.001308
this when 0 < p < 0.50, to do Z = -Z; in case that 0.50 < p < 1.0 use: p = 1 - p in Equation (29), without change Z.
Non-stationary LN3 distribution
The quantile function of the Log-Normal distribution of three non-stationary fitting parameters (LN31) is similar to Equation (23), but it uses conditional moments and variables (Serago & Vigel, 2018):
To quantify ax[w with Equation (24), Equations (20) and (21) are used and to evaluate μx[w by means of expression (25) the Equation (21) is used. In Equation (31), σ y is defined with the expression (26), due to the fact that is only a function of γ x (remember Equation (14)).
Stationary LP3 distribution
If a series of annual extreme hydrological values (y) defined as y = ln (x) follows a Pearson type III distribution, also known as a three parameter Gamma, then variable x has a Log-Pearson type III distribution (LP3). Predictions associated with a certain return period (Tr), which is the reciprocal of the exceedance probability, are estimated with the expressions (WRC, 1977; Kite, 1977; Bobée & Ashkar, 1991):
and
In Equation (32), K p is the so-called frequency factor, it is a standardized Pearson type III variable whose approximation is achieved based on the standardized normal variable Z (Equations (29) and (30)) and the corrected asymmetry coefficient (γ c ), with the following equations (Kite, 1977):
being:
and
Non-stationary LP3 distribution
Equation (33) is actually the quantile function of the LP3 distribution, whose non-stationary version (LP31) is obtained by substituting the conditional moments of y (Equations (12) and (13)), that is (Serago & Vogel, 2018):
The constant values of the previous expression, from left to right, are defined in Equations: (6), (9), (4), (34), (7), (9) and (5), these last three, squared. For the calculation of K p with the Equation (34), Serago and Vogel (2018) establish a different expression to Equation (35) for the asymmetry coefficient and define it as follows:
Stationary GVE Distribution
The Generalized Extreme Values (GVE) distribution includes three families of functions: the Gumbel that are straight lines on the Gumbel-Powell probability paper (Chow, 1964), the Fréchet that are curves with upward concavity and lower limit, and the Weibull that have downward concavity and upper limit. Its quantile function is the following:
in which, u, α and k are the location, scale and shape parameters and p is the probability of non-exceedance. Bhunya, Jain, Ojha y Agarwal (2007) have proposed expressions to estimate the fitting parameters of the GVE, based on the mean (ˉx), standard deviation (σx) and coefficient of asymmetry (Yx), that is, based on the non-conditional moments; these are: when -0.70 ≤ γ x ≤ 1.15
and when γ x ≥ 1.15
for -0.50 ≤k ≤ 0.50, we have:
when 0.010 ≤ k ≤ 0.50
and when -0.50 ≤ k ≤ 0.010, the following Equation (44) is applied:
The values of ˉx and σ x are obtained with Equations (6) and (7), using x instead of y. Serago and Vogel (2018) use Equation (11) to estimate the coefficient of asymmetry (γ x ).
Non-stationary GVE Distribution
When equations of the conditional moments of x are applied, defined by Equations (20), (21), (22), and (19), in Equations (40) to (44), the fitting parameters of GVE distribution the non-stationary (GVE1) are obtained, and they are named:ux[w, ax[w and kx[w, whose quantile function is (Serago & Vogel, 2018):
Standard error of fit
The standard error of fit (EEA) has been established as a quantitative objective indicator, because it evaluates the standard deviation of the differences between the observed values and those estimated with the FDP that is tested; in this study the models: LN3, LP3, GVE, LN31, LP31 and GVE1. Its expression is the following (Kite, 1977):
in which, n and np are the number of data and of fitting parameters, in this case three, for the stationary FDP and four for the non-stationary ones; X i are the data ordered from least to highest and ˆXi are the values estimated with the stationary quantile function (Equations (23), (33), and (39)) and non-stationary (Equations (31), (37), and (45)), for a probability of non-exceedance estimated with the Blom formulas for the models LN3, LN31, LP3 and LP31 and of Gringorten for the GVE and GVE1 distributions, as suggested by Serago and Vogel (2018):
where, m is the order number of the datum, with 1 for the least and n for the highest.
Approach of the probabilistic analysis
The EEA helps to select, among different distributions applied to the data or sample available, the one of better fit. Logically, such models must be of same type, stationary or non-stationary. Then, in each record to be processed, the LN3 and LN31 distributions are applied first, then the LP3 and LP31 and finally, the GVE and GVE1; their EEA values are analyzed and the predictions sought are adopted. In this process, when the EEAs are similar, a distribution can be adopted based on hydrological safety judgments, that is, the one that reports the most unfavorable or critical predictions.
By means of Equations (31), (37) and (45) predictions are calculated with return periods (Tr) of 2, 25, 50 and 100 years, through the record period, applying the variable w i in the interval from 1 to n. The first prediction is the median, since its probability of non-exceedance (F) is 50% and the following three are calculated for complementary probabilities, to define its higher and lower value (Park, Kang, Lee, & Kim, 2011), that is, for the following values: F = 0.96 and F = 0.04 for the Tr of 25 years; F = 0.98 and F = 0.02 for the Tr of 50 years and F = 0.99 and F = 0.01 for the Tr of 100 years.
Predictions that use the variable w i equal to the size of the record (n) correspond to the end of the historical record. Future predictions are possible using as magnitude of the variable w i , the sum of the size of the record (n) plus the lapse in years to the future. Extrapolations of the predictions were made in three future dates, 10, 25 and 50 years after the available record is concluded.
Mudersbach and Jensen (2010) establish that the hydrological design of hydraulic works must be reliable or safe until the end of its useful life or future date. If the record of floods or annual PMD available to estimate the CDs, shows an upward trend, then their predictions should be estimated at such future date so that their hydrological sizing is correct and not unsafe.
In this context, Salas et al. (2018) have suggested shortening the useful life values to 25 or 50 years and at the same time making the design and construction of hydraulic works more versatile, so that they allow for extensions and/or modifications at lower costs for society.
Records to be processed
The first series of extreme hydrological data corresponds to the annual maximum flows of the Neponset River in Norwood, Massachusetts, U.S.A., in the period from 1939 to 2015 (n = 77). This drainage basin has 89.8 km2, with 16% of its extension of impermeable area, which has increased its maximum flows, but it is also a river with small reservoirs for municipal and industrial supplies (Serago & Vogel, 2018). The approximate values read from a logarithmic figure of these authors are shown in Table 1 and Figure 1; it is observed that such record shows slight upward trend.
Table 1 Annual maximum flows (Q, m3/s) of the Neponset River, U.S.A. (Serago & Vogel, 2018).
| No. | Q | No. | Q | No. | Q | No. | Q |
|---|---|---|---|---|---|---|---|
| 1 | 12.4 | 21 | 9.0 | 41 | 23.9 | 61 | 13.3 |
| 2 | 6.4 | 22 | 6.9 | 42 | 12.6 | 62 | 9.3 |
| 3 | 6.7 | 23 | 8.9 | 43 | 8.7 | 63 | 20.8 |
| 4 | 8.5 | 24 | 10.4 | 44 | 18.5 | 64 | 7.3 |
| 5 | 6.5 | 25 | 13.5 | 45 | 12.9 | 65 | 9.6 |
| 6 | 5.7 | 26 | 11.0 | 46 | 26.7 | 66 | 12.4 |
| 7 | 7.2 | 27 | 8.6 | 47 | 8.7 | 67 | 14.1 |
| 8 | 11.7 | 28 | 5.5 | 48 | 11.2 | 68 | 24.2 |
| 9 | 6.0 | 29 | 11.0 | 49 | 19.6 | 69 | 14.4 |
| 10 | 11.2 | 30 | 31.7 | 50 | 10.9 | 70 | 16.2 |
| 11 | 4.7 | 31 | 17.9 | 51 | 8.9 | 71 | 16.9 |
| 12 | 5.0 | 32 | 19.2 | 52 | 17.6 | 72 | 33.0 |
| 13 | 7.1 | 33 | 8.4 | 53 | 9.0 | 73 | 12.9 |
| 14 | 9.4 | 34 | 12.1 | 54 | 7.0 | 74 | 11.0 |
| 15 | 11.1 | 35 | 12.3 | 55 | 11.1 | 75 | 13.3 |
| 16 | 12.3 | 36 | 11.4 | 56 | 10.3 | 76 | 14.1 |
| 17 | 41.1 | 37 | 8.5 | 57 | 7.1 | 77 | 14.2 |
| 18 | 13.7 | 38 | 19.4 | 58 | 10.4 | - | - |
| 19 | 7.0 | 39 | 11.1 | 59 | 21.7 | - | - |
| 20 | 10.8 | 40 | 15.0 | 60 | 30.7 | - | - |
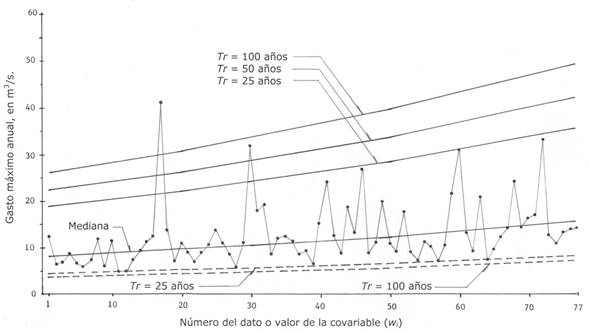
Figure 1 Chronological data series and estimated prediction curves with the LP31 distribution in a hydrometric station of the Neponset River, USA.
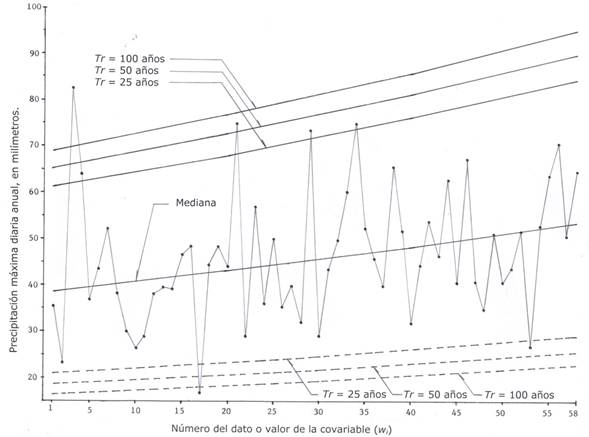
La second series of extreme hydrological data that was analyzed, comes from Campos-Aranda (2016) and corresponds to the annual maximum daily precipitations (PMD) ) of the Zacatecas climatological station, in the city of the same name in Mexico, with a record of 58 years in the period from 1953 to 2010. The series has an upward trend, as shown in Figure 2.
Results and discussion
Predictions in the Neponset River
Table 2 shows a selection of the predictions obtained during the historical record with the LN31 distribution. The basic parameters of this non-stationary fitting were: ρ = 0.414, β = 0.0085, ax[w=3.807, ux[w=2.4830, γc=1.83614 and σy=0.5182. Table 3 shows the EEA and the predictions of the stationary LN3 model with a = 0.5879 and μy=2.3842 and of the non-stationary, logically at the end of the historical record (n) and in the three future scenarios proposed.
Table 2 Predictions (m3/s) in the historical record obtained with the LN31 distribution in the Neponset River, USA.
| No. | Data | Median | Tr = 25 years | Tr = 50 years | Tr = 100 years | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 12.4 | 8.3 | 17.6 | 4.5 | 20.3 | 4.2 | 23.0 | 3.9 |
| 10 | 11.2 | 9.0 | 19.0 | 4.9 | 21.9 | 4.5 | 24.9 | 4.2 |
| 20 | 10.8 | 9.7 | 20.7 | 5.3 | 23.8 | 4.9 | 27.0 | 4.6 |
| 30 | 31.7 | 10.6 | 22.5 | 5.8 | 25.9 | 5.3 | 29.4 | 5.0 |
| 40 | 15.0 | 11.5 | 24.5 | 6.3 | 28.2 | 5.8 | 32.0 | 5.4 |
| 50 | 10.9 | 12.6 | 26.6 | 6.9 | 30.7 | 6.3 | 34.9 | 5.9 |
| 60 | 30.7 | 13.7 | 29.0 | 7.5 | 33.4 | 6.9 | 37.9 | 6.4 |
| 70 | 16.2 | 14.9 | 31.6 | 8.1 | 36.3 | 7.5 | 41.3 | 7.0 |
| 77 | 14.2 | 15.8 | 33.5 | 8.6 | 38.5 | 7.9 | 43.8 | 7.4 |
Table 3 Predictions (m3/s) in the stationary LN3 and non-stationary LN31 distributions in the Neponset River, USA.
| Applied distribution | EEA (m3/s) | Return periods in years | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| LN3 | 1.00 | 17.4 | 21.7 | 27.5 | 32.0 | 36.8 | 48.8 | 54.4 |
| LN31 (n) | 4.67 | 22.3 | 27.1 | 33.5 | 38.5 | 43.8 | 57.0 | 63.2 |
| LN31 (n+10) | 4.67 | 24.3 | 29.5 | 36.4 | 41.9 | 47.7 | 62.1 | 68.8 |
| LN31 (n+25) | 4.67 | 27.6 | 33.4 | 41.4 | 47.6 | 54.1 | 70.5 | 78.1 |
| LN31 (n+50) | 4.67 | 34.1 | 41.3 | 51.1 | 58.8 | 66.8 | 87.1 | 96.5 |
Table 4 shows a portion of the predictions obtained during the historical record with the LP31 distribution. The basic parameters of this non-stationary fitting were: ˉy=2.4543 and σy=0.4569, ρ = 0.414, β = 0.0085 and γc = 0.53338. Table 5 shows the EEA and the predictions of the stationary LP3 model with γc = 0.53878 and of the non-stationary, at the end of the historical record (n) and in the three future dates analyzed.
Table 4 Predictions (m3/s) in the historical record obtained with the LP31 distribution in the Neponset River, USA.
| No. | Data | Median | Tr = 25 years | Tr = 50 years | Tr = 100 years | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 12.4 | 8.1 | 18.8 | 4.4 | 22.2 | 4.1 | 26.1 | 3.8 |
| 10 | 11.2 | 8.8 | 20.2 | 4.8 | 24.0 | 4.4 | 28.1 | 4.1 |
| 20 | 10.8 | 9.6 | 22.0 | 5.2 | 26.1 | 4.8 | 30.6 | 4.4 |
| 30 | 31.7 | 10.4 | 24.0 | 5.6 | 28.4 | 5.2 | 33.3 | 4.8 |
| 40 | 15.0 | 11.3 | 26.1 | 6.1 | 30.9 | 5.6 | 36.3 | 5.3 |
| 50 | 10.9 | 12.3 | 28.4 | 6.7 | 33.6 | 6.1 | 39.5 | 5.7 |
| 60 | 30.7 | 13.4 | 30.9 | 7.3 | 36.6 | 6.7 | 42.9 | 6.2 |
| 70 | 16.2 | 14.6 | 33.6 | 7.9 | 39.8 | 7.3 | 46.7 | 6.8 |
| 77 | 14.2 | 15.5 | 35.7 | 8.4 | 42.3 | 7.7 | 49.6 | 7.2 |
Table 5 Predictions (m3/s) in the stationary LP3 and non-stationary LP31 distributions in the Neponset River, USA.
| Applied distribution | EEA (m3/s) | Return periods in years | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| LP3 | 0.75 | 16.8 | 21.3 | 28.0 | 33.8 | 40.3 | 58.8 | 68.6 |
| LP31 (n) | 2.71 | 22.4 | 27.8 | 35.7 | 42.3 | 49.6 | 69.9 | 80.4 |
| LP31 (n+10) | 2.71 | 24.4 | 30.3 | 38.8 | 46.0 | 54.0 | 76.1 | 87.5 |
| LP31 (n+25) | 2.71 | 27.7 | 34.4 | 44.1 | 52.2 | 61.3 | 86.4 | 99.3 |
| LP31 (n+50) | 2.71 | 34.2 | 42.5 | 54.4 | 64.5 | 75.7 | 106.7 | 122.7 |
Table 6 shows a part of predictions during the historical record, estimated with the GVE1 distribution, with γx[w=2.2731 and parameters of fit: ux[w=14.015, ax[w =4.742 and kx[w=-0.139. On the other hand, Table 7 shows the EEA and the predictions of the stationary GVE model with γ x = 1.8361, u = 9.817, α = 4.607 and k = -0.101, as well as the non-stationary at the end of record and in the future in the three dates proposed.
Table 6 Predictions (m3/s) in the historical record obtained with the GVE1 distribution in the Neponset River, USA.
| No. | Data | Median | Tr = 25 years | Tr = 50 years | Tr = 100 years | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 12.4 | 8.3 | 17.4 | 4.7 | 20.3 | 4.3 | 23.4 | 3.9 |
| 10 | 11.2 | 9.0 | 18.8 | 5.1 | 21.9 | 4.6 | 25.3 | 4.3 |
| 20 | 10.8 | 9.8 | 20.5 | 5.5 | 23.8 | 5.0 | 27.5 | 4.6 |
| 30 | 31.7 | 10.6 | 22.3 | 6.0 | 25.9 | 5.5 | 30.0 | 5.0 |
| 40 | 15.0 | 11.6 | 24.2 | 6.5 | 28.2 | 5.9 | 32.6 | 5.5 |
| 50 | 10.9 | 12.6 | 26.4 | 7.1 | 30.7 | 6.5 | 35.5 | 6.0 |
| 60 | 30.7 | 13.7 | 28.7 | 7.7 | 33.4 | 7.0 | 38.6 | 6.5 |
| 70 | 16.2 | 14.9 | 31.2 | 8.4 | 36.4 | 7.7 | 42.0 | 7.1 |
| 77 | 14.2 | 15.8 | 33.1 | 8.9 | 38.6 | 8.1 | 44.6 | 7.5 |
Table 7 Predictions (m3/s) in the stationary GVE and non-stationary GVE1 distributions in the Neponset River, USA.
| Applied distribution | EEA (m3/s) | Return periods in years | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| GVE | 1.01 | 17.3 | 21.5 | 27.2 | 31.9 | 36.8 | 49.7 | 55.9 |
| GVE1 (n) | 4.65 | 21.9 | 26.5 | 33.1 | 38.6 | 44.6 | 60.9 | 69.1 |
| GVE1 (n+10) | 4.65 | 23.9 | 28.9 | 36.0 | 42.0 | 48.5 | 66.3 | 75.2 |
| GVE1 (n+25) | 4.65 | 27.1 | 32.8 | 40.9 | 47.7 | 55.1 | 75.2 | 85.4 |
| GVE1 (n+50) | 4.65 | 33.5 | 40.5 | 50.6 | 58.9 | 68.1 | 92.9 | 105.5 |
Based on the values of the EEA shown in Tables 3, 5 and 7, the predictions or results of LP3 and LP31 distributions are adopted, against those of the LN3 and LN31, GVE and GVE1 models, because they lead to their lowest magnitudes, indicating with it, a better fitting for the available data. Predictions of the non-stationary LP31 distribution were found to be the most severe or critical, thus providing greater safety in the hydrological design at the end of the useful life of 10, 25 or 50 years.
Figure 1 shows the chronological series of the Neponset River floods, U.S.A. and their estimated prediction curves with the non-stationary LP31 distribution.
Predictions in the Zacatecas station
Table 8 shows a part of the predictions obtained during the historical record with the LN31 distribution. The basic non-stationary parameters of fit were: ρ = 0.298, β = 0.0057, ax[w=-66.8647, μx[w=4.7920,γ c = 0.42827 and σy=0.1411. Table 9 shows the EEA and predictions of the stationary LN3 model with a = -54.6459 and μ y = 4.6091 and of the non-stationary, logically at the end of the historical record (n) and in the three future scenarios proposed.
Table 8 Predictions (mm) in the historical record obtained with the LN31 distribution in the Zacatecas station, México.
| No. | Data | Median | Tr = 25 years | Tr = 50 years | Tr = 100 years | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 35.1 | 38.8 | 63.3 | 19.7 | 68.2 | 16.9 | 72.7 | 14.4 |
| 10 | 26.4 | 40.9 | 66.6 | 20.8 | 71.7 | 17.8 | 76.5 | 15.2 |
| 20 | 44.0 | 43.3 | 70.5 | 22.0 | 75.9 | 18.8 | 81.0 | 16.1 |
| 30 | 29.2 | 45.8 | 74.6 | 23.3 | 80.4 | 19.9 | 85.7 | 17.0 |
| 40 | 32.0 | 48.5 | 79.0 | 24.6 | 85.1 | 21.1 | 90.8 | 18.0 |
| 50 | 41.0 | 51.3 | 83.6 | 26.1 | 90.0 | 22.3 | 96.1 | 19.1 |
| 58 | 65.0 | 53.7 | 87.5 | 27.3 | 94.2 | 23.3 | 100.5 | 19.9 |
Table 9 Predictions (mm) of the stationary LN3 and non-stationary LN31 distributions in the Zacatecas station, Mexico.
| Applied distribution | EEA (mm) | Return periods in years | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| LN3 | 1.52 | 58.4 | 65.6 | 73.9 | 79.5 | 84.8 | 96.0 | 100.6 |
| LN31 (n) | 8.93 | 68.9 | 77.6 | 87.5 | 94.2 | 100.5 | 114.1 | 119.6 |
| LN31 (n+10) | 8.93 | 72.9 | 82.1 | 92.6 | 99.7 | 106.4 | 120.7 | 126.6 |
| LN31 (n+25) | 8.93 | 79.4 | 89.4 | 100.8 | 108.6 | 115.9 | 131.5 | 137.8 |
| LN31 (n+50) | 8.93 | 91.5 | 103.0 | 116.2 | 125.1 | 133.5 | 151.5 | 158.8 |
Table 10 shows a portion of the estimated predictions during the historical record with the LP31 distribution. The basic parameters of this non-stationary fitting were: ˉy=3.7962, σy=0.3218 , ρ = 0.298, β = 0.0057 and γ c = -0.50869. Table 11 shows the EEA and the predictions of the stationary LP3 model with γc = -0.51495 and of the non-stationary at the end of the record and in the three future dates analyzed.
Table 10 Predictions (mm) in the historical record obtained with the LP31 distribution, in the Zacatecas station, Mexico.
| No. | Data | Median | Tr = 25 years | Tr = 50 years | Tr = 100 years | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 35.1 | 38.9 | 61.3 | 21.0 | 65.3 | 18.6 | 69.0 | 16.6 |
| 10 | 26.4 | 40.9 | 64.5 | 22.2 | 68.8 | 19.6 | 72.6 | 17.4 |
| 20 | 44.0 | 43.3 | 68.2 | 23.4 | 72.8 | 20.7 | 76.9 | 18.4 |
| 30 | 29.2 | 45.8 | 72.2 | 24.8 | 77.0 | 21.9 | 81.3 | 19.5 |
| 40 | 32.0 | 48.5 | 76.4 | 26.3 | 81.5 | 23.2 | 86.1 | 20.7 |
| 50 | 41.0 | 51.3 | 80.9 | 27.8 | 86.3 | 24.6 | 91.1 | 21.9 |
| 58 | 65.0 | 53.7 | 84.7 | 29.1 | 90.3 | 25.7 | 95.4 | 22.9 |
Table 11 Predictions (mm) of the LP3 stationary and LP31 non-stationary distributions in the Zacatecas station, Mexico.
| Applied distribution: | EEA (mm) | Return periods in years | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| LP3 | 1.51 | 58.6 | 65.8 | 73.6 | 78.7 | 83.3 | 92.6 | 96.1 |
| LP31 (n) | 4.46 | 68.1 | 76.0 | 84.7 | 90.3 | 95.4 | 105.5 | 109.3 |
| LP31 (n+10) | 4.46 | 72.1 | 80.5 | 89.6 | 95.6 | 100.9 | 111.7 | 115.7 |
| LP31 (n+25) | 4.46 | 78.5 | 87.6 | 97.6 | 104.1 | 109.9 | 121.6 | 126.0 |
| LP31 (n+50) | 4.46 | 90.4 | 101.0 | 112.5 | 120.0 | 126.7 | 140.1 | 145.2 |
Table 12 shows part of the predictions during the historical record, estimated with the GVE1 distribution, with Yx|w=2.1646 and fitting parameters: ux[w=46.955, ax[w=10.950 and kx[w=-0.131. In contrast, Table 13 show the EEA and the predictions of the stationary GVE model with γ x = 0.4283, u = 40.896, α = 13.166 and k = 0.152, as well as the non-stationary, record term and in the three future dates proposed.
Table 12 Predictions (mm) in the historical record estimated with the GVE1 distribution in the Zacatecas station, Mexico.
| No. | Data | Median | Tr = 25 years | Tr = 50 years | Tr = 100 years | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 35.1 | 36.9 | 65.4 | 25.4 | 74.3 | 24.1 | 83.9 | 23.0 |
| 10 | 26.4 | 38.9 | 68.9 | 26.7 | 78.2 | 25.3 | 88.3 | 24.2 |
| 20 | 44.0 | 41.2 | 72.9 | 28.3 | 82.8 | 26.8 | 93.5 | 25.6 |
| 30 | 29.2 | 43.6 | 77.1 | 29.9 | 87.6 | 28.4 | 99.0 | 27.1 |
| 40 | 32.0 | 46.1 | 81.6 | 31.7 | 92.7 | 30.0 | 104.7 | 28.7 |
| 50 | 41.0 | 48.8 | 86.4 | 33.5 | 98.1 | 31.8 | 110.9 | 30.4 |
| 58 | 65.0 | 51.1 | 90.4 | 35.1 | 102.7 | 33.3 | 116.0 | 31.8 |
Table 13 Predictions (mm) of the stationary GVE and non-stationary GVE1 distributions in the Zacatecas station, Mexico.
| Applied distribution | EEA (m3/s) | Return periods in years | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| GVE | 1.44 | 58.6 | 66.0 | 74.2 | 79.6 | 84.5 | 93.8 | 97.2 |
| GVE1 (n) | 9.45 | 65.1 | 75.6 | 90.4 | 102.7 | 116.0 | 151.9 | 169.8 |
| GVE1(n+10) | 9.45 | 68.9 | 80.0 | 95.7 | 108.7 | 122.8 | 160.8 | 179.7 |
| GVE1(n+25) | 9.45 | 75.0 | 87.1 | 104.2 | 118.4 | 133.7 | 175.1 | 195.7 |
| GVE1(n+50) | 9.45 | 86.5 | 100.4 | 120.1 | 136.4 | 154.1 | 201.8 | 225.5 |
Based on the values of the EEA shown in Tables 9, 11 and 13 the predictions or results of the GVE and LP31 models are adopted, because they lead to their lowest magnitudes, thus indicating a better fitting to the available data. The predictions of the three stationary models are almost identical. The GVE1 function reports more extreme or critical predictions, but its EEA is more than the double obtained with the LP31 distribution; therefore they were not selected.
Figure 2 shows the chronological series of annual PMD of the Zacatecas climatological station, Mexico and its straight lines of estimated predictions with non-stationary LP31 distribution.
Conclusions
The frequency analysis (AF) of records of annual extreme hydrological data that are not homogeneous, when presenting trend, will be quite frequent in the immediate future, due to the effects of global or regional climate change and the physical impacts of alterations in the basins of drainage, such as urbanization and deforestation, as well as the construction of reservoirs.
Another aspect that will favor such non-stationary AF is to provide hydrological protection at the end of the useful life of a hydraulic work. The above, requires taking into account the trend observed in the record to be processed, in order to obtain more reliable predictions at a future date, when the useful life of the hydraulic work that is dimensioned ends. This is important when the record shows upward trend.
The method described and developed by Serago and Vogel (2018) and also exposed by Salas et al. (2018), based on the conditional moments of y = ln(x) and of x, which are the available data, allows us to obtain, in a simple way the functions of non-stationary quantile, of three of the most used probability distributions and highest universality in the AF of floods and other extreme annual hydrological data, which are the Log-Normal (LN3), the Log-Pearson type III (LP3) and the Generalized Extreme Values (GVE).
The method uses time as a covariate, with a linear trend and therefore the non-stationary models LN31, LP31 and GVE1 are fitted. Quantile functions, which allow obtaining their predictions sought, are only slightly more complicated than their stationary versions, which makes this approach quite practical, to obtain predictions in trending records, within them, at their end and in future dates. This was demonstrated in the two numerical applications described; whose selection of better fitting achieved was based on the standard error of fit, a technique widely used in the AFs.
Referencias
Aissaoui-Fqayeh, I., El Adlouni, S., Ouarda, T. B. M. J., & St. Hilaire, A. (2009). Développement du modèle log-normal non-stationnaire et comparaison avec le modèle GEV non-stationnaire. Hydrological Science Journal, 54(6), 141-1156. [ Links ]
Álvarez-Olguín, G., & Escalante-Sandoval, C. A. (2016). Análisis de frecuencias no estacionario de series de lluvia anual. Tecnología y ciencias de agua, 7(1), 71-88. [ Links ]
Bhunya, P. K., Jain, S. K., Ojha, C. S., & Agarwal, A. (2007). Simple parameter estimation technique for three-parameter generalized extreme value distribution. Journal of Hydrologic Engineering, 12(6), 682-689. [ Links ]
Bobée, B., & Ashkar, F. (1991). The Gamma Family and derived distributions applied in Hydrology (Chapter 1, pp. 1-12). Littleton, USA: Water Resources Publications. [ Links ]
Campos-Aranda D. F. (2016). Modelo probabilístico simple para análisis de frecuencias en registros hidrológicos extremos con tendencia. Tecnología y ciencias del agua, 7(3), 171-186. [ Links ]
Campos-Aranda, D. F. (2018). Ajuste con momentos L de las distribuciones GVE, LOG y PAG no estacionarias en su parámetro de ubicación, aplicado a datos hidrológicos extremos. Agrociencia, 52(2), 169-189. [ Links ]
Chow, V. T. (1964). Statistical and probability analysis of hydrologic data. frequency analysis. In: Chow, V. T. (ed.). Handbook of applied hydrology (pp. 8.1-8.42). New York, USA: McGraw-Hill Book Co. [ Links ]
El Adlouni, S., Ouarda, T. B. M. J., Zhang, X., Roy, R., & Bobée, B. (2007). Generalized maximum likelihood estimators for the nonstationary generalized extreme value model. Water Resources Research, 43(W03410), 1-13. [ Links ]
El Adlouni, S., & Ouarda, T. B. M. J. (2008). Comparaison des méthodes d’estimation des paramètres du modèle GEV non stationnaire. Revue des Sciences de L’Eau, 21(1), 35-50. [ Links ]
Johnson, F., & Sharma, A. (2017). Design rainfall. In: Singh, V. P. (ed.). Handbook of applied hydrology (Chapter 125, pp. 125.1-125.13) (2nd ed.). New York, USA: McGraw-Hill Education. [ Links ]
Khaliq, M. N., Ouarda, T. B. M. J., Ondo, J. C., Gachon, P., & Bobée, B. (2006). Frequency analysis of a sequence of dependent and/or non-stationary hydro-meteorological observations: A review. Journal of Hydrology, 329(3-4), 534-552. [ Links ]
Kite, G. W. (1977). Frequency and risk analyses in hydrology (Chapter 9, pp. 105-122 and chapter 12, 156-168). Fort Collins, USA: Water Resources Publications. [ Links ]
López-de-la-Cruz, J., & Francés, F. (2014). La variabilidad climática de baja frecuencia en la modelación no estacionaria de los regímenes de las crecidas en las regiones hidrológicas Sinaloa y Presidio-San Pedro. Tecnología y ciencias del agua, 5(4), 79-101. [ Links ]
Majumdar, P. P., & Kumar, D. N. (2012). Floods in a changing climate. Hydrologic Modeling. Cambridge, United Kingdom: International Hydrology Series (UNESCO) and Cambridge University Press. [ Links ]
Meylan, P., Favre, A. C., & Musy, A. (2012). Predictive hydrology. A Frequency analysis approach (Chapter 3, pp. 29-70). Boca Raton, USA: CRC Press. [ Links ]
Mudersbach, C., & Jensen, J. (2010). Nonstationary extreme value analysis of annual maximum water levels for designing coastal structures on the German North Sea coastline. Journal of Flood Risk Management, 3(1), 52-62. [ Links ]
Nguyen, T. H., El Outayek, S., Lim, S. H., & Nguyen, T. V. T. (2017). A systematic approach to selecting the best probability models for annual maximum rainfalls - A case study using data in Ontario (Canada). Journal of Hydrology , 553, 49-58. [ Links ]
Park, J. S., Kang, H. S. Lee, Y. S., & Kim, M. K. (2011). Changes in the extreme daily rainfall in South Korea. International Journal of Climatolog y, 31(15), 2290-2299. [ Links ]
Prosdocimi, I., Kjeldsen, T. R., & Svensson, C. (2014). Non-stationarity in annual and seasonal series of peak flow and precipitation in the UK. Natural Hazards and Earth System Sciences, 14(5), 1125-1144. [ Links ]
Rao, A. R., & Hamed, K. H. (2000). Flood frequency analysis (Theme 1.8, pp. 12-21). Boca Raton, USA: CRC Press . [ Links ]
Salas, J. D., Obeysekera, J., & Vogel, R. M. (2018). Techniques for assessing water infrastructure for nonstationary extreme events: A review. Hydrological Sciences Journal, 63(3), 325-352. [ Links ]
Serago, J. M., & Vogel, R. M. (2018). Parsimonious nonstationary flood frequency analysis. Advances in Water Resources, 112(February), 1-16. [ Links ]
Serenaldi, F., & Kilsby, C. G. (2015). Stationarity is undead: Uncertainty dominates the distribution of extremes. Advances in Water Resources, 77(March), 17-36. [ Links ]
Stedinger, J. R., Vogel, R. M., & Foufoula-Georgiou, E. (1993). Frequency analysis of extreme events. In: Maidment, D. R. (ed.). Handbook of hydrology (Chapter 18, pp. 1-66). New York, USA: McGraw-Hill Inc. [ Links ]
Teegavarapu, R. S. V. (2012). Precipitation variability and teleconnections. Chapter 6 (pp. 169-192). In: Floods in a changing climate. Extreme precipitation. Cambridge, United Kingdom: International Hydrology Series (UNESCO) and Cambridge University Press. [ Links ]
Vogel, R. M., Yaindl, C., & Walter, M. (2011). Nonstationarity: Flood magnification and recurrence reduction factors in the United States. Journal of the American Water Resources Association, 47(3), 464-474. [ Links ]
WRC, Water Resources Council. (1977). Guidelines for determining flood flow frequency (revised edition). In: Bulletin # 17A of the Hydrology Committee. Washington, DC, USA: Water Resources Council. [ Links ]
Zelen, M., & Severo, N. C. (1972). Probability functions. In: Abramowitz, M., & Stegun, I. A (eds.). Handbook of mathematical functions (Chapter 26, pp. 925-995) (9t h pr.). New York, USA: Dover Publications. [ Links ]
Received: July 30, 2018; Accepted: January 14, 2019











 text in
text in