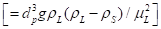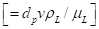Introduction
Fluidization is an operation in which solid particles enters in contact with a fluid acquiring fluid characteristics (Mukherjee, Mishra, & Ran, 2009) and is known for its wide use since the early 50’s. In conventional fluidization, the solid particles have a higher density than the fluid therefore the bed solids can be fluidized by an upwards flow, in the case of a bed of particles having a density smaller than the fluid (usually liquid), the bed is fluidized by a downwards flow of the liquid and it is usually called inverse fluidized bed (Bimal, Uma, & Sudip, 2010). Among the advantages presented by the latest are high mass transfer rates, minimum carry over of coated microorganisms due to less solid attrition, efficient control of biofilm thickness and ease of refluIdization in case of power failure (Garcia, Buffière, & Elmaleh, & Moletta, 1998; Bimal et al., 2010). These significant advantages found many applications of inverse fluidized beds in biochemical processes like ferrous iron oxidation and aerobic and anaerobic biological wastewater treatment like treatment of wine distillery wastewater. Previous studies on liquid-solid inverse fluidized bed reactor (IFBR) dealt with different hydrodynamic characteristics such as pressure drop, minimum fluidization velocity and bed void fraction e.g. (Fan, Muroyama, & Chern, 1982; Karamanev & Nivkolov, 1992; Renganathan & Krishnaiah, 2007).
The bed void fraction is one of the important design parameters that determine the height of fluidized bed during steady state operation. Under normal operating conditions, fluidized bed reactors operate under steady state. However, unsteady state operation is encountered during start-up and shut-down of the reactor and due to fluctuations in liquid flow rates. Such conditions may prevail in a wastewater effluent treatment plant where an IFBR is mostly used. Therefore, information on the unsteady state bed expansion is required for better understanding of the fluid dynamics under transient conditions, which will lead to better control of the reactor and for the design of IFBR an industrial scale (Renganathan & Krishnaiah, 2007).
In many processes there are particles with diameter different in the particles of the bed greatly modifies its porosity due to the particle’s size and density variation. This modification in the bed porosity affects the proper operation and control of the fluid bed reactor. Therefore, it is important to have a reliable model in order to estimate bed porosity for design and scale-up of fluid bed reactors.
Numerous models have been proposed to predict the bed porosity in fluidized beds with spherical and non-spherical particles, but only it includes a range of Reynolds number from 200 to 6,000. The major and most used until today by several authors (Yang & Renken, 2003; Akgiray & Soyer, 2006; Renganathan & Krishnaiah, 2007; Fuentes, Scena, Aguirre, & Mussati, 2008; Soyer & Akgiray, 2009) are: Richardson and Zaki (1954), Wen and Yu (1966), Ramamurthy and Subbaraju (1973), Riba and Couderc (1977), Fan et al. (1982), and Setiadi (1995) models.
Mathematical models for prediction of traditional fluidized bed porosity can be used in inverse fluidization, nevertheless, some authors disagrees with this practice (Wen & Yu, 1966; Ramamurthy & Subbaraju, 1973; Hyun, 2001).
Therefore the general aim of this work is to study the hydrodynamic of a liquid-solid inverse fluidized bed reactor with different polypropylene spherical particles diameters and different densities to propose a mathematic model to estimate bed porosity in a range of Reynolds number from 5.5 to 200, which has not been studied in this reactor and this hydrodynamic characteristics are very important to low fluidization rates in biotechnology process.
Materials and methods
Liquid and solid phase
Water at 20 oC was used as fluid work in an inverse fluidization reactor and polypropylene spherical particles of average diameter 4.00, 4.16 and 4.18 mm and density of 808, 825 and 867 kg/m3 were used as solid phase. The sphericity is an important measure that describes how round a particle is defined as the ratio of the surface area of a sphere with the same volume as the given particle to the surface area of the particle itself, therefore the solid particles in this work have a sphericity of 1.
Installation
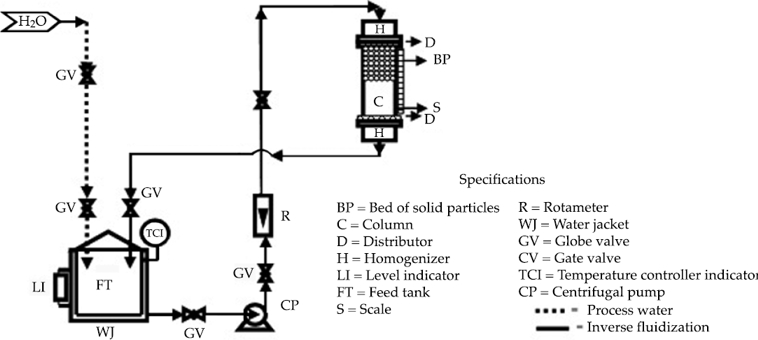
A schematic diagram of the fluidized bed reactor used in this work is shown in Figure 1. As shown, the experimental setup included a 0.04 m of internal diameter (ID) and 0.50 m high cylindrical glass column. The work fluid was stored in a tank, and pumped into the column by a 1/8 HP little giant centrifugal pump, model 583002. The flow rate in the reactor was measured with a rotameter and fixed in the range between 0.95-9.5 (l min-1).
Start-up
The inverse fluidization with each particles lot was done of the following way: The inverse fluidized bed reactor was filled with water at 20 oC, the water was used as a liquid phase, the polypropylene particles were introduced for the upper part of the reactor and the initial height bed was measured with the calibrated scale in centimeter. The flow rate was increased 6 times more (0.63, 0.88, 1.00, 1.13, 1.26 and 1.38 l min-1) and the heights bed was measured. Figure 2 shows the inverse fluidization reactor at different flowrates.
Particle density
Particle density was determined by Standard test methods for specific gravity of solids by water pycnometer (ASTM D854-14) to determining their volume and mass, this method was repeat three times The volume was measured using a pycnometer filled with light oil (density 750 kg/ m3) and the mass was measured in an analytical balance Sartorius ±1x10-7 kg. The particle density was calculated by dividing the mass by the volume.
The density media was determined by pycnometer (ASTM D854-14). The viscosity media was measured with a Malvern SV-10 vibratory viscosimeter.
Results and discussion
Hydrodynamic study
The different equations that relate the bed porosity with the fluid superficial rate can be classified into three main groups Fan et al. (1982). The first group is based on a relationship that dependence between velocity and initial velocity (U/Ui) and porosity (ε). The Richarson and Zaki (1954) equation is the most popular of this group. The second group of equations is based on the drag for multiparticulates systems. This is usually given as a function of Reynolds number (Re) and Archimedes number (Ar). Ramamurthy and Subbaraju (1973), and Riba and Couderc (1977) are typical for this group.
The third group is based on the ratio obtained from the balance of forces acting on a particle isolated (gravity, floating, drag) and assume that applies to all particles in the bed as the equation of Wen and Yu (1966) for spherical and non-spherical particles using a shape factor (ψ) and Reynolds numbers are in the range 200 to 6000. Table 1 shows the function of porosity shown Wen and Yu (1966), Riba and Couderc (1977), and Rammamurthy and Subaraju (1973) which were chosen because they have a lower standard deviation in the case of spherical particles of uniform size.
d p Particle diameter
f Function
f(ε) Porosity function
g gravity
μ L Liquid viscosity
ρ L Liquid density
ρ p Particle density
Predictive model proposed and comparison with other models
The comparison of the results was made by plotting the porosity function obtained from values proposed by Wen and Yu (1966), Ramamurthy and Subbaraju (1973), Riba and Courdec (1977) and this work, versus experimental bed porosity data.
The model proposed in this paper was designed using the inertial drag coefficient (CI) Becker (1959) for Re < 200. The data used in the model proposed in this work were Wilhelm and Kwauk (1948) and the experimental data obtained in this work. The model to calculate the porosity of spherical particles and the application intervals as shown in table 2.
Table 2 Model proposed in this work to calculate the porosity of spherical particles.
Ramamurty and Subaraju (1973) porosity function fits the experimental data tendency, but do not represent the experimental bed porosity. The plot (figure 3) shows an experimental underestimation for experimental data between 0.5 and 0.73 of bed porosity, this deviation can be attributed to the principal assumption by these authors that the solid particles are represented as an ensemble moving about points considered as nodes of an imaginary lattice through whose free volume the fluid is flowing. It is important to notice that this model was developed for annular fluid.
Riba and Courdec (1977) model fits the experimental data tendency but the plot shows a slight experimental underestimation for experimental data between 0.55 and 0.63 of bed porosity.
Wen and Yu (1966) model fits has a good correlation of bed porosity data; the standard deviation was 1.2%.
The mathematical model proposed in this work fits well the trend of the experimental bed porosity data for spherical particles which was well represented by this function in the interval of porosity from 0.47 to 0.73; the standard deviation was 0.9%.
The new model has several advantages because Wen and Yu (1966), Riba and Courderc (1977), and Ramammurthy and Subaraju (1973), restrict their model to traditional fluidization (upward flow) and spherical particles. Furthermore the new model is considerably simple in form, it can be used for spherical particles, but includes a term of inertial drag coefficient proposed by Becker (1959) which includes a shape factor to non-spherical particles.
The figure 3 shows the graph of the function of porosity that results from using the correlation Wen and Yu, Riba and Couderc (1977), Ramamurthy and Subbaraju (1973), and the model proposed in this work.
The table 3 shows a comparison of the standard deviation of the equation proposed in this work and the equations published in literature.
Conclusions
The experiments were conducted in an inverse fluidized bed reactor at different flowrates. The results show that the approach to the balance of forces acting on a particle, namely gravity, the buoyancy force and the drag applied to a normal flow, i.e., from the bottom up, is valid for case of a reverse flow (from top to bottom). The equation Wen and Yu (1966) and the equation proposed in this work are showing a lower standard deviation to the experimental data.
The equation proposed in this paper can make a better approach by the balance of forces with a larger number of data in the literature. It is important to identify the study variables, also, to a dimensional analysis, since grouping variables in dimensionless numbers such as the Reynolds and Archimedes allow the handling of mathematical models takes just a simple manner, also, dimensionless numbers handling facilitates the design and scale reactors.











 text new page (beta)
text new page (beta)