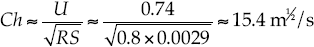Introducción
Un hecho observado en los procesos fluviales es que existe una relación evidente entre las fuerzas que tallan los cursos naturales de agua y la forma y proporciones de los lechos de los mismos. Así, por ejemplo, en un cauce estrecho la fuerza del agua tallará de manera preponderante las paredes laterales (A), tratando de ganar más ancho; por otro lado, en cauces anchos, esta fuerza tenderá a profundizar el cauce (B). De esta forma, los procesos de "tallaje" en un sentido u otro buscarán equilibrarse de modo dinámico en cierto punto (C) (Figura 1).
Ocurre entonces un "equilibrio dinámico" cuando la sección transversal del cauce logra un valor tal que las fuerzas de "tallaje" en distintas direcciones no predominan la una sobre la otra y la geomorfología del flujo se mantiene aproximadamente en el tiempo (Leopold & Maddock, 1954).
Este estado de "equilibrio dinámico" en el proceso de formación del cauce por el movimiento continuo del agua no sólo se interpreta en términos de los cambios en las áreas efectivas de las paredes resistentes del lecho (efecto), sino también, e indisolublemente, mediante la velocidad del flujo, pendiente y rugosidad superficial (causas). El efecto final de este proceso de estabilización en sentidos contrarios: no sólo afecta la dimensión transversal sino también la longitudinal. Así, desde el punto de vista del perfil longitudinal del lecho, es que aquellos sitios donde haya una mayor pendiente, la deposición de sedimento tratará de suavizar el perfil y que en aquellos sitios de pendiente "suave", la socavación intentará "empinar" el perfil, siendo Sb la pendiente (Figura 2).
El "equilibrio dinámico" en la formación de los cauces puede entonces verse como una tendencia a la igualación de las tasas de "deposición" y "socavación" de sedimentos sobre el lecho tanto en el perfil transversal como en el longitudinal. Como quiera que el agente controlador directo de estos dos procesos opuestos es la velocidad media del fluido, este parámetro no toma por supuesto valores arbitrarios sino aquellos compatibles con la tendencia explícita al mencionado equilibrio.
Ahora bien, para un grado dado de resistencia del lecho (dependiente de las características físicas de las partículas de ese lecho), esto es, lo que se denomina "rugosidad", la pendiente como fuerza motriz del movimiento del fluido será un cierto valor que ajusta de forma concordante la interacción velocidad-deposición-socavación (Hack, 1957).
Por lo tanto, el mencionado "equilibrio dinámico" se refleja sobre tasas del transporte de masa en el interior del sistema. Esto se analiza en seguida.
Transporte de masa en el interior del sistema bajo la condición de "equilibrio dinámico" en los cauces naturales
Considerando ahora un sistema cerrado evolucionado totalmente irreversible, Ω por el principio de conservación de la energía, en el que la energía mecánica entrante se convierte enteramente en energía térmica por degradación, se tiene que:
En este caso se puede ver que la pendiente Sb aporta un componente inicial de energía potencial gravitatoria, ΔU (Ζ), el cual es transformado en energía cinética, ΔK (movimiento del agua), el cual finalmente es transformado por entero en calor, ΔQ (Figura 3).
También se ha demostrado que en los sistemas hidrológicos en los que se estudian los cambios de la geomorfología es importante aplicar además el segundo principio de la termodinámica o principio de la entropía. En estas condiciones, para un sistema cerrado irreversible isotérmico en el que toda la energía potencial U se transforma en calor, Q, se puede mostrar entonces que la entropía es constante (Leopold & Langbein, 1962).
Entonces la entropía interna (por irreversibi-lidad), Si, expulsada en la frontera del sistema, con T como temperatura absoluta, se puede escribir como:
Si se parte de la definición del gas ideal para la nube de trazador PV = nRT, donde P es la presión, V es el volumen, n el número de moles y R = 8.31 J/(K*mol), la constante universal de los gases, reemplazando la temperatura en la ecuación anterior, se tiene:
Considerando ahora la presión P = f/A, f como fuerza, área como A = ΔY * ΔX, y volumen como V = ΔY * ΔX * ΔZ, con Y = ancho, X = largo y Ζ = profundidad del flujo, se tiene:
Dividiendo cada miembro por el volumen y sabiendo que ΔV = q * Δt, donde q es el caudal, queda finalmente:
Esto implica que la producción de entropía interna por unidad de caudal lleva de continuo a la disminución de la energía relativa disponible por unidad de volumen. La entropía creciente dentro del sistema genera una distribución cada vez más uniforme de energía dentro del volumen de Ω. El miembro derecho de esta ecuación puede ser interpretado entonces como la descripción de la distribución más probable de energía en el sistema, la cual es constante según la interpretación estadística de Boltzmann (Leopold & Langbein, 1962), en los que los distintos eventos energéticos en el volumen de control Ω son equiprobables:
Y
El "equilibrio dinámico" (estado estable) en los cauces naturales va a significar entonces no sólo que el flujo neto de masa en las fronteras del sistema es aproximadamente nulo en virtud de la equivalencia entre socavación y deposición (conservación de la masa), sino también que los eventos individuales internos descritos mediante los intercambios de energía serán equivalentes, uniformes o indistinguibles en el volumen de control por su equiprobabilidad.
Cálculo de las diferentes tasas de transporte de masa en un sistema de flujo en "equilibrio dinámico"
Es interesante ahora estudiar las consecuencias concretas de la "equiprobabilidad" para diversos sucesos de intercambio de energía dentro del sistema, en este caso la traslación de diferentes porciones de masa dentro del sistema, sea ésta una masa disuelta o suspendida en un sistema hídrico.
Se debe partir del hecho de que en un flujo natural la energía potencial estará representada como se indica a continuación:
Supóngase que un cierto intercambio elemental de energía dentro de un sistema que por motivos de su "localidad" está asociado más bien a un incremento de masa que a uno de altura:
Si el sistema es estacionario (equilibrio dinámico), entonces los diferentes intercambios de energía derivados de las permutas de masa de partículas similares de soluto tendrán igual probabilidad. Entonces los propios intercambios de masa, como distribución estadística en el tiempo, estarán "igualados" también por este principio.
Corresponde por lo tanto a una distribución estadística constante similar a la de la ecuación (5), sólo que en lugar de la variable "energía potencial" U se tiene la variable masa M. Interesa además establecer la distribución repartida además en el tiempo.
Para analizar su distribución en el tiempo se define la traslación en el espacio de un elemento de masa Δmj en un tiempo Δtj. Entonces la "tasa de transporte de masa" es igual a la razón entre el diferencial de masa movilizada en un punto sobre el diferencial de tiempo en que ocurre este evento (Figura 4).
Matemáticamente, esto se define así:
La tasa de transporte de masa "general" para el tramo considerado, definida por su valor representativo desde el punto de vista estadístico, es la esperanza matemática de los componentes individuales de transporte (Spiridonov & Lopatkin, 1973). Por lo tanto su definición representativa en todo el dominio del volumen de control Ω será:
Pero como los elementos discretos de masa transportada son equivalentes (iguales por equiprobables), entonces queda:
Finalmente:
O sea, la tasa de transporte de masa "general" es convergente con las tasas de transporte de masa "locales" en "estado estable" del cauce, consideradas ellas como indistinguibles (iguales). En este caso, lo general replica a lo particular.
Cálculo de las diferentes tasas de transporte de masa en un sistema de flujo en "equilibrio dinámico": caso de la masa disuelta
Aunque la masa transportada en el flujo puede ser suspendida o disuelta, es posible en estado estable realizar un "balance detallado" (Prigogine & Kondepudi, 1998) de ambos tipos de masas desde la óptica de la equivalencia entre "tasas de transporte locales" y "tasa de transporte general". Ello es consecuencia del equilibrio dinámico en cuanto en esta condición cada transformación elemental es balanceada por su contraparte específica, en el esquema concreto en el que hayan sido planteadas.
Entonces, si:
Se sigue que:
Y:
Por estas razones se aplicará el principio de equivalencia entre tasas de transporte "locales" y "generales" al componente disuelto, lo que facilita su análisis por medio de trazadores.
Cálculo de la tasa de transporte de masa disuelta "general" en el sistema
En condiciones de estado estable, en un flujo natural, el aporte de solutos a la corriente es una característica propia de la cuenca y del caudal al cual se incorporan estas sustancias. Si se llama "Co" a la concentración base resultante de este aporte y "q" al caudal correspondiente, la relación típica es una curva hiperbólica (Hem, 1985) (Figura 5).
Dicha relación tiene esta forma toda vez que entre mayor sea el caudal para un aporte dado de solutos en el lecho, se tendrá un mayor volumen para disolver, esto es, menor concentración:
Atendiendo a la parte dimensional, la "constante" k es miligramos por segundo, o sea, una tasa de transporte de masa.
Tasa de transporte de masa disuelta "local" medida por trazadores
Una forma de medir las tasas "locales" de transporte de masa en los flujos naturales es por medio de trazadores, los cuales, vertidos de forma súbita en un punto del tramo del cauce, se pueden considerar como "testigos" locales del movimiento "individual" de la masa en el sistema Ω (Figura 6).
Para entender de forma apropiada cómo el trazador puede cumplir la misión de medir la tasa local de transporte de masa es necesario estudiar algunos puntos de la dinámica de los mismos.
Velocidad media del flujo en función de los datos del transporte dispersivo
En artículos anteriores, los autores han definido esta función de la siguiente forma: relacionando dos velocidades, una la de dispersión del trazador, Vdisp, de naturaleza irreversible y medida por su desplazamiento random walk, y la otra la de advección, U, que no debe confundirse con la energía potencial, como factor integrante. Aquí Δ y τ son parámetros característicos de desplazamiento y fase del movimiento Gaussiano mono-dimensional de la pluma de trazador (Constaín & Lemos, 2011; Constaín, 2013):
Como quiera que Vdisp mida la rapidez con que las partículas de trazador se alejan de modo recíproco, es una función que representa la reacción del sistema a la ruptura súbita del equilibrio químico y por lo tanto es un potencial termodinámico. La naturaleza especial de φ(t) se puede caracterizar diciendo que es una función de estado del sistema, definida mediante la siguiente ecuación:
El cálculo teórico de la función φ(t), como ya se ha explicado en otros artículos de los autores (Constaín & Corredor, 2013), se hace a partir del tiempo medido entre los dos puntos de inflexión de la curva Gaussiana experimental dividida por el tiempo de transporte y multiplicada por una constante. De la ecuación (26) se puede establecer una definición para la velocidad media advectiva:
Despejando E:
Debe notarse aquí que el tiempo característico Gaussiano τ es diferente a la variable independiente t, pues la primera se refiere al tiempo en el cual la separación aleatoria de las partículas ocurre mientras esta distancia promedio es Δ, mientras que la escala temporal general se asocia más bien con el efecto advec-tivo de U. La relación entre ambos tiempos se puede establecer mediante una dinámica del tipo Poisson-Svedberg (Constaín, Peña, Mesa, & Acevedo, 2014):
La función de estado φ( t )
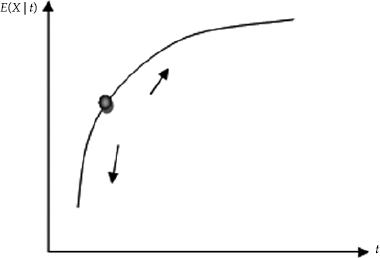
Debido a que φ(t) es un potencial termodiná-mico y en consonancia con la ecuación (19), su valor inicial es el mismo que el final, por lo tanto es una curva unimodal, con un pico en "a", cuya parte utilizable siempre es después de t = ɑ (Figura 7). El flanco ascendente corresponde a los fenómenos transitorios y muy rápidos que ocurren cuando el soluto conservativo se acopla en el líquido.
Debido a que la velocidad Vdisp va disminuyendo en la medida que el sistema tiende de forma irreversible hacia el equilibrio después de t = ɑ, entonces φ(t) es descendente en su flanco más externo. Debe tenerse en cuenta que hay valor máximo para φ(t ≈ 0) ≈ 2.16.
La descripción de la pluma de soluto vista por diferentes observadores
La transformación de Galileo para pasar de un sistema inercial a otro se incluye de manera parcial en el argumento exponencial de la ecuación clásica de Fick, con M, la masa de soluto y A, la sección transversal del flujo (Fischer, 1967):
Sin embargo, dicha transformación es completa sólo si el coeficiente E es una función del tiempo, tal como se describe en la ecuación (21). Ahora reemplazándola en la ecuación (23), se tiene con: √2πβ ≈ 1.16:
La particularidad de esta ecuación (fórmula modificada de Fick) es que reproduce bastante bien las curvas experimentales de trazador, como se mostrará en la sección "Pantallas de la medición desde el equipo IDF". Supóngase que se realiza un vertimiento lateral de trazador desde la orilla de un flujo turbulento, tal como se muestra en la Figura 6 con la pluma de trazador evolucionando en el tramo; en este caso, el caudal comprendido por el "tubo de corriente" que limita la pluma de trazador, ql, es un valor "local", toda vez que, en principio, el trazador no ha cubierto todo el volumen del flujo real ni participa de la velocidad plena del flujo (Ul < U) ni su ancho efectivo es el de todo el flujo (Wl < W) ni tampoco que su profundidad (en la orilla) es la del cauce (hl < h):
Debe recordarse, además, que en un cauce natural turbulento vale aproximadamente una distribución transversal de velocidades (línea punteada), tal como se muestra en la Figura 8. Se muestra también en la gráfica la anchura "local" de la pluma de trazador (línea roja). Se asume que la profundidad es el valor medio de todo el cauce (para simplificar, hl = h).
Modelo para la evolución de la concentración pico del trazador en el tiempo, Cp(t)
La concentración pico del trazador, definida como en la ecuación (26), es muy importante, pues va a permitir verificar de forma global la validez de los principios aquí propuestos:
Ahora se puede mostrar que su evolución temporal se puede definir más sucintamente mediante la siguiente definición empírica:
El factor multiplicador "α" es una función del tiempo que debe ser ajustada a partir de los datos experimentales en diferentes instantes. Es conveniente partir de un modelo simple exponencial descendiente del tipo:
Definición de la tasa de transporte de masa local mediante la ecuación modificada de Fick
A partir de los conceptos desarrollados anteriormente se puede ahora definir la "tasa de transporte de masa local" con base en experimentos de trazador. En el punto de medición para la ecuación (33) se tiene que la tasa local de transporte de masa es aproximadamente igual a la siguiente ecuación, con Cp como concentración pico para el trazador, considerado conservativo para que su disminución a lo largo del tramo sea debida sólo al efecto dispersivo:
Igualación de la tasa de transporte de masa "general" y "local" en un flujo en "equilibrio dinámico"
En correspondencia con lo establecido en el apartado 4, ecuación (15) para la masa disuelta observada de forma "general" y "local" en un cauce natural, se tiene que para un flujo en equilibrio dinámico se cumple aproximadamente que:
O sea:
Esta ecuación es bastante significativa, toda vez que φ(t) es, como ya se dijo, una función de estado y tiene una significación termodinámica muy especial en tanto que refleja propiedades "generales" del sistema en el que evoluciona, aunque sea medida en zonas "locales", así trae información del estado particular del proceso de avance de la mancha de trazador (ql y Cp), pero también de los procesos generales para el cauce en equilibrio dinámico (como q y Co). Por esta razón se puede considerar a la ecuación (31) como una definición universal para dicha función, es decir, válida para todo el ámbito del flujo en el tramo considerado. Ahora, como quiera que ql y Cp son parámetros de la pluma función del tiempo, el cálculo de la ecuación (31) debe hacerse en un tiempo especial que hemos denominado "tiempo de acople", tc. En este instante se puede considerar que las condiciones termodinámicas predominantes en el estado estable hacen que la información de todo el proceso se refleje en un solo cálculo. Dentro de dicha información estará naturalmente la correspondiente a la pendiente en su calidad de causa ("driving force") del proceso.
Papel del "tiempo de acople", tc, en la formación de la pluma de soluto
En virtud de lo explicado en los párrafos anteriores, la ecuación (31) y el principio en el cual está basada es importante desentrañar los mecanismos de formación de las plumas de trazador una vez que el soluto conservativo penetra en el agua. De esta forma, la concentración pico inicial del soluto no es independiente de la concentración base en su entorno físico y tampoco es independiente del valor del caudal general. Es como si en el tiempo de formación de la pluma, su evolución estuviese predeterminada por los parámetros generales del flujo, cuya información de alguna forma se transfiere a ese elemento de flujo; es muy probable que la naturaleza de esa transmisión sea de naturaleza electroquímica. La concentración de base Co es en principio "constante", por lo tanto el ajuste requerido para obtener la concentración pico apropiada es función del tiempo; esto implica que su valor de ajuste debe ser calculado en un tiempo especial tc, como ya se dijo.
La pendiente como dato clave de la condición de "equilibrio dinámico"
Una observación cuidadosa de lo expresado en la introducción con respecto al papel preponderante de la pendiente del flujo como agente básico de las transformaciones energéticas en los cauces y por lo tanto en las condiciones de establecimiento del "equilibrio dinámico" que lleva al balance de masa de socavación y de deposición en el tramo indica que la función de estado φ(t) no es independiente del mecanismo por el cual el flujo establece el valor preciso y específico de la pendiente, Sb, en el proceso de formación del cauce.
Se debe decir que este proceso físico de fijación de la pendiente que actúa en específico para las condiciones de velocidad media, caudal y rugosidad tiene su símil en el proceso analítico para establecer cuál es el coeficiente longitudinal de dispersión del trazador (función de la pendiente), que vale realmente para el tramo en su conjunto. En virtud de este símil se podría decir que la función de estado que sirve para la aplicación del principio de la equivalencia de las tasas de transporte es la misma que también se usa para la determinación de la pendiente.
Para evidenciar esto es necesario hacer referencia a la ecuación de Elder y a su interpretación más reciente desde la teoría de los trazadores.
Cálculo de la pendiente de un flujo en equilibrio dinámico según Elder
En 1959, Elder propuso su ya célebre definición para el coeficiente longitudinal de dispersión, E (Elder, 1959); h es la profundidad media del flujo; Sb, la pendiente como fuerza generatriz gravitacional del movimiento del flujo, y g es la aceleración de la gravedad:
Por supuesto, si la ecuación (21) se equipara con la ecuación (32), se debe aceptar que la definición de Elder de E debe ser también una función del tiempo. Es decir, puede moverse a través de la curva misma (Figura 9).
Ubicación específica del coeficiente longitudinal de dispersión en la curva función del tiempo
En realidad no basta afirmar que la definición de pendiente de Elder es una función del tiempo, sino también determinar en qué punto concreto de la curva estará situado el valor correspondiente (punto negro en la curva de la Figura 9). Para realizar esta tarea es necesario primero estimar el rango aproximado del tiempo a explorar (Constaín, 2014).
Estimación del tiempo de acople "tc"
Se parte de la ecuación (31), que da un panorama muy directo de las diferentes relaciones entre los parámetros de interés. Así, por ejemplo, si se tiene en cuenta que p máximo puede valer 2.16, entonces la razón del numerador y del denominador tienen que ser del mismo orden. Además de esto, para ríos grandes en el trayecto inicial del trazador q >> q, que implica que Cp >> Co.
Cálculos de la pendiente, coeficiente de Chezy y función de estimación
Una vez estimado el valor probable del tiempo que vale para aplicar la relación entre tasas de transporte, se procede a despejar la pendiente de la ecuación de Elder. Este procedimiento se debe hacer mediante "prueba y error", para ir determinando para varios valores de E cuál es el que más se ajusta. El ajuste se hace mediante una función de estimación, F, que se desarrolla en seguida. Es prudente comenzar por aplicar el valor inicial encontrado mediante trazadores, según la ecuación (21). Si este primer intento no se ajusta, se usarán valores diferentes hasta lograr un ajuste apropiado, según se verá después en la aplicación experimental:
La función de estimación se establece igualando las dos definiciones de velocidad media del flujo, la nueva representada en la ecuación (20) y la clásica para flujo uniforme de Chezy, con R como radio hidráulico y Ch como el coeficiente de Chezy:
A partir de allí se establece la función de estimación, F, que medirá la bondad de la aproximación que se haga para la pendiente mediante valores diversos de E. El ajuste es "ideal" cuando la función F es igual al coeficiente numérico de la ecuación de Elder:
Y, por lo tanto, en condición ideal:
Entonces, la función de estado φ(t) que aparece en las ecuaciones (31) y (36) tiene el mismo valor que garantiza la validez del concepto de "equilibrio dinámico" en el tramo estudiado del cauce natural, ajustado de forma apropiada por la pendiente. La pendiente ajusta de modo simultáneo la dispersión y equivalencia de tasas de transporte.
Cuando hay que realizar varias tentativas de "prueba y error" se debe recurrir de nuevo a la ecuación (21) para disponer de otros valores de E para determinar la pendiente con la debida aproximación.
Aplicación del método a la determinación de la pendiente en un rio de montaña de mediano tamaño en Colombia
Aspectos del cauce
Se escogen los resultados experimentales con (35) trazador salino realizados en el año 2007 en el río Pance en el Valle del Cauca, región sur occidental de Colombia. En la Figura 10 se muestran diversos aspectos del tramo medido.
Instrumentación utilizada y aspectos del vertimiento de trazador iónico
Para las mediciones con trazador iónico (sal común) se utilizó un avanzado dispositivo denominado IDF (Inírida Deep Flow) desarrollado en Colombia para operar en "tiempo real", potente interfaz gráfica que permite un trabajo interactivo, así como guardar los aforos en memoria. En la Figura 11 se muestran algunos aspectos de la instrumentación e inyección de trazador "aguas arriba". En el experimento mostrado se usó una masa de sal común de 9 060 gramos disueltos inicialmente en agua, en un balde de unos 20 litros.
Pantallas de la medición desde el equipo IDF
En la Figura 12 se tienen fotografías de las pantallas del instrumento con los datos respectivos de la medición.
En la primera foto (izquierda superior) se muestra la curva experimental (trazo irregular) y sobre puesto el modelo teórico logrado con la aplicación de la ecuación (33), dado los datos del Cuadro 1. La cercanía del modelo teórico y la curva experimental es una garantía de la certeza de los datos obtenidos por el instrumento.
La foto superior derecha corresponde al cálculo del caudal mediante el principio de conservación de la masa (área bajo la curva de trazador). La foto inferior izquierda corresponde a la pantalla del instrumento en la que se muestra el cálculo de la función de estado p (t) para la medición a X = 400 m. La foto inferior derecha muestra algunos datos calculados por el software del equipo.
Cuadro de datos numéricos
El Cuadro 1 condensa las informaciones recogidas por el IDF en la medición sobre el cauce. Se parte del dato de distancia del vertimiento y la medición que fue de X = 400 m para un ancho estimado de W = 20 metros.
Desarrollo del estudio
Estudio de tc mediante la relación de Elder
Después de hacer varias tentativas en tiempos muy cercanos al instante del vertimiento, se mostrará en seguida que la dinámica correcta se puede caracterizar por el tiempo de acople tc = 2.6 s después del vertimiento, o sea a X = 1.9 m, si se considera que vale una velocidad media de U = 0.74 m/s. Los cálculos detallados para considerar que esto es correcto se muestran a continuación.
Cálculo de Elder para la pendiente para tc = 2.6 s
Se inicia el proceso calculando el coeficiente longitudinal de dispersión, suponiendo que para este tiempo tan inmediato al vertimiento la función de estado φ ≈ 2.16:
Se calcula luego la pendiente probable, suponiendo que la profundidad media se conserva en todo el tramo considerado:
Se calcula luego el coeficiente aproximado de Chezy:
Se calcula luego la función de estimación, F:
Este valor se considera satisfactorio en tanto es el ideal de 5.93 (coeficiente de Elder), y entonces se pueden tomar como correctos los valores aproximados calculados antes. Se estima que este tiempo es el correcto para calcular la equivalencia de tasas de transporte.
Cálculo de la razón de tasas de transporte a tc = 2.6 s
Se empieza calculando de manera aproximada el coeficiente transversal de difusión, el ancho local de la pluma, para luego estimar el caudal local:
La razón de caudales es entonces:
Por lo tanto, la razón de concentraciones en estado estable a tc = 2.6 s es:
La concentración pico del trazador a tc = 2.6 s después del vertimiento, con una masa de 9.06 kg de soluto, es:
Verificación de los cálculos realizados mediante la determinación general de la curva de la Concentración pico, Cp(t)
Lo que se debe hacer ahora es construir esta función Cp(t) en función de los diferentes datos en instantes diferentes: A, en el punto de medición a t = 539 s; B, en el punto de acople a tc = 2.6 s.
En el instante mismo de la inyección, a t = 0 s. Para realizar la tarea completa se debe partir de lo explicado en el apartado "Modelo para la evolución de la concentración pico del trazador en el tiempo, Cp(t)". Se comienza por conocer los distintos valores experimentales de "α":
A. Punto de medición a t = 539 s:
B. Cálculo en el punto de acople a t = 2.6 s:
Como se dijo, uno puede constatar que "α" es -como φ(t)- una función del tiempo. Por tal razón es necesario proponer un modelo exponencial descendiente para este parámetro, de tal forma que el modelo coincida con los datos experimentales:
Se puede mostrar que para que la expresión ajuste, la constante "k" vale 0.00234, y entonces la concentración pico Cp(t) reproduce de forma aproximada los datos experimentales para el tiempo de acople y medición (Figura 13a y b ).
Verificación de la congruencia de los cálculos
Tener el modelo general para Cp (t) es muy ventajoso, pues se puede encontrar de forma aproximada la concentración pico del trazador en el momento mismo del vertimiento, el cual se considera tipo "slug" (súbito).
De forma razonable se puede decir que la concentración pico inicial debe ser del mismo orden que la concentración de la mezcla inicial al momento de verter, es decir, la razón entre la masa de trazador vertido (9.060 kg) y el volumen aproximado del balde de agua utilizado (20 litros):
De acuerdo con la ecuación (49), se tiene que para un tiempo muy cercano a cero, la concentración pico del trazador es:
Es decir, un valor bastante cercano al esperado, con un error porcentual de 7%. Esta situación se puede ver gráficamente en la Figura 14.
Conclusiones
De lo analizado en este artículo se pueden identificar los siguientes aspectos sobre el experimento de trazadores iónicos en el tramo del río Pance:
Las aplicaciones experimentales de los linea-mientos teóricos presentados aquí fueron exitosas en la medida que los diferentes datos son altamente congruentes entre sí, aceptándose que representan -dentro del límite de las aproximaciones y simplificaciones usadas- una descripción fiable de la evolución del trazador y su relación con los parámetros geomorfológicos e hidráulicos.
El concepto básico aquí discutido es el de "equivalencia de tasas de transporte" en los cauces naturales en la parte local y en la general; esto es una consecuencia de las propiedades estadísticas del flujo en condiciones estacionarias que aproximan el "equilibrio dinámico" analizado en detalle por varios autores del siglo pasado, en especial Luna B. Leopold. Para un sistema fluvial cerrado, evolucionando de modo irreversible, no sólo se conserva la masa en sus fronteras sino que las tasas de transporte son iguales en cada punto del interior. Es un proceso en el cual la información global se incorpora en los fenómenos individuales.
Esta equivalencia permite definir con precisión los mecanismos de formación de las plumas de trazador en los cauces naturales y por lo tanto de interés para los especialistas que estudian los procesos de contaminación en los estudios de calidad de aguas. El hecho de tener una información congruente en hidráulica, transporte dispersivo y geomorfología facilita mucho la calibración de los modelos a usarse de manera posterior.











 text new page (beta)
text new page (beta)