Artículos técnicos

 

Pronóstico de caudales con Filtro de Kalman Discreto en el río Turbio

 

Streamflow Forecasting for the Turbio River using the Discrete Kalman Filter

 

Fernando González-Leiva, Laura Alicia Ibáñez-Castillo*
Universidad Autónoma Chapingo, México
*Autor de correspondencia

Juan B. Valdés
The University of Arizona at Tucson, USA

Mario Alberto Vázquez-Peña, Agustín Ruiz-García
Universidad Autónoma Chapingo, México

 

Dirección institucional de los autores

M.I. Fernando González Leiva
Dra. Laura Alicia Ibáñez Castillo
Dr. Mario Alberto Vázquez Peña
Dr. Agustín Ruiz García

Posgrado en Ingeniería Agrícola y Uso Integral del Agua
Universidad Autónoma Chapingo
Km. 38.5 carretera México-Texcoco
56230 Chapingo, Estado de México, México
Teléfono: +52 (595) 9521 551
fernando.gleiva@gmail.com libacas@gmail.com mvazquezp@correo.chapingo.mx agustinruizg@gmail.com

Dr. Juan B. Valdés

The University of Arizona at Tucson
Hydrology and Water Resources
United States of America
1133 James E. Rogers
Harshbarger Bldg. Room 318E
Tucson AZ 85721, USA
jvaldes@email.arizona.edu

 

Recibido: 22/05/2014.
Aceptado: 19/01/2015.

 

Resumen

Se propuso la implementación del algoritmo del Filtro de Kalman Discreto (DKF) junto con un modelo autorregresivo con entrada exógena (ARX) para realizar el pronóstico de caudales a corto plazo con 24, 48, 72 y 96 horas de anticipación en la cuenca del río Turbio, localizada en el estado de Guanajuato y parte del estado de Jalisco, México, vulnerable a inundaciones durante los periodos de lluvias que se presentan normalmente en la zona. La información de precipitación y caudal disponible con las que se realizaron los pronósticos corresponde a las series de los años 2003 y 2004. Los resultados obtenidos indican que los pronósticos realizados un paso hacia adelante, es decir, con un tiempo de 24 horas de anticipación, presentaron los mejores ajustes en términos de Nash-Sutcliffe, MSE y RMSE, que los pronósticos realizados a 48, 72 y 96 horas de anticipación.

Palabras clave: Filtro de Kalman, modelos autorregresivos, pronósticos de caudales a corto plazo.

 

Abstract

This paper proposes the use of the discreet Kalman filter (DKF) along with an autoregressive model with exogenous inputs (ARX) for short-term streamflow forecasting with lead times of 24, 48, 72 and 96 hours. This model was applied to the Turbio River basin, located in the state of Guanajuato and a portion of the state of Jalisco, Mexico. This area is vulnerable to flooding during rainy periods which normally occur in the region. The forecasting was based on available precipitation and streamflow data from the years 2003 and 2004. The results indicate that the forecasts performed with one-step ahead, that is with a 24-hour lead time, present better fits than 48, 72 and 96-hour lead times in terms of Nash-Sutcliffe, MSE and RMSE.

Keywords: Kalman filter, autoregressive models, short-term streamflow forecasting.

 

Introducción

Como consecuencia de la variabilidad del clima (IPCC, 2007; Mendoza et al., 2009; Montero-Martínez, Ojeda-Bustamante, Santana-Sepúlveda, Prieto-González, & Lobato-Sánchez, 2013) y de su previsible influencia en la magnitud de la gravedad, la frecuencia y el impacto de las avenidas y sequías, durante los últimos años ha aumentado la importancia de las predicciones como estimaciones de los estados futuros de un fenómeno hidrológico. Dichas predicciones son esenciales para el funcionamiento eficaz de la infraestructura hídrica y para la atenuación de desastres naturales provocados según las condiciones ambientales (WMO, 2009).

De acuerdo con Valdés, Mejía-Velázquez, & Rodríguez-Iturbe (1980), en la predicción de caudales se puede postular una relación causal entre la precipitación en varios puntos de la cuenca, a diferentes instantes de tiempo y un caudal medio en un punto de salida para un día determinado. Esta relación causal, denominada función de respuesta, puede ser representada como un modelo de caja negra. Los modelos autorregresivos han sido ampliamente usados en la hidrología y los recursos hídricos desde inicios de la década de 1960 para la modelación anual y periódica en series de tiempo de tipo hidrológico.

La aplicación de estos modelos ha sido atractiva en la hidrología; en especial, la forma autorregresiva tiene dependencia del tiempo y por la facilidad para ser usados (Salas, Delleur, Yevjevich, & Lane, 1980; Box, Jenkins, & Reinsel, 2013). En los últimos años, el algoritmo del Filtro de Kalman se ha propuesto para realizar el pronóstico de caudales en los sistemas hidrológicos, operado junto con modelos matemáticos de lluvia- escurrimiento en cuencas hidrográficas (Moradkhani, Sorooshian, Gupta, & Houser,2005; Xie & Zhang, 2010; Lü et al., 2013; Morales-Velázquez, Aparicio, & Valdés, 2014; Abaza, Anctil, Fortin, & Turcotte, 2014), haciendo énfasis en la estimación óptima de los parámetros de estado de los modelos utilizados mediante la técnica conocida como asimilación de datos (Moradkhani, DeChant, & Sorooshian, 2012; Liu et al., 2012; Shi, Davis, Zhang, Duffy, & Yu, 2014; Samuel, Coulibaly, Dumedah, & Moradkhani, 2014, Liu, et al., 2015; Yucel, Onen, Yilmaz, & Gochis, 2015; Li, Ryu, Western, & Wang, 2015). Sin embargo, para usar estos modelos se requieren series continuas y completas de caudales, algo que podrían no tener países en desarrollo, como México. Según Perevochtchikova (2013), en las bases de datos a nivel climatológico, CLICOM, y de aguas superficiales, BANDAS, que posee México, existe una problemática recurrente: poca accesibilidad, marcadas diferencias sectoriales y vacíos en las series de tiempo, lo que deriva en dificultades para su uso en las tareas de comparación y análisis de evolución espacial y temporal, sistematización de datos, y construcción de indicadores y de modelos a escala local.

El Filtro de Kalman Discreto (DKF) fue propuesto por Kalman (1960) como una solución recursiva por el método de mínimos cuadrados al problema de filtrado lineal de datos discretos. Es un procedimiento matemático que opera por medio de un mecanismo de predicción y corrección. Este algoritmo pronostica el nuevo estado a partir de una estimación previa, añadiendo un término de corrección proporcional al error de predicción, de tal forma que este último es minimizado estadísticamente. Por esta razón, si se tiene conocimiento del sistema dinámico, las estadísticas del sistema ruidoso, los errores de medición y las condiciones iniciales, se puede estimar el estado para un sistema dinámico (Gelb, 1974; Simon, 2001; Welch & Bishop, 2006).

El pronóstico de caudales en cuencas hidrográficas forma parte de los procedimientos que permiten tomar decisiones con criterios fundamentados en la planificación del riesgo que busca mitigar los impactos negativos ocasionados por las avenidas en campos específicos de la hidrología, como la regulación de embalses y la emisión de alertas tempranas ante inundaciones en zonas con presencia de población civil. En México, Morales-Velázquez, Aparicio y Valdés (2014) evaluaron la utilidad del algoritmo del Filtro de Kalman Discreto (DKF) en el pronóstico de avenidas, con fines de regular los caudales en la presa Ángel Corbino Corzo o Peñitas, perteneciente al sistema hidroeléctrico Grijalva.

En el presente trabajo se propuso la implementación del algoritmo del Filtro de Kalman Discreto (DKF) junto con un modelo autorregresivo con entrada exógena ARX para realizar el pronóstico de caudales a corto plazo, con 24, 48, 72 y 96 horas de anticipación en la cuenca del río Turbio, localizada en el estado de Guanajuato y parte del estado de Jalisco, México, vulnerable a inundaciones durante los periodos de lluvias registradas en la zona.

 

Materiales y métodos

Descripción de la cuenca

La figura 1 muestra la localización y representación de la cuenca del río Turbio, la cual pertenece a la Región Hidrológica 12 Lerma Santiago, ubicada en los estados de Guanajuato y Jalisco, entre los 20° 32’ 42" y los 21° 21’ 18" de latitud norte, y entre los 101° 27’ 82" y los 102° 17’ 57" de longitud oeste. Las principales poblaciones que se encuentran en la cuenca son Ciudad de León, San Francisco del Rincón, Purísima de Bustos y Manuel Doblado. El área total de la cuenca es de 3 322 km² hasta la estación hidrométrica Las Adjuntas, ubicada en los 20° 40’ 32" de latitud norte y 101° 50’ 40" de longitud oeste, de los cuales 58.8% pertenece al estado de Guanajuato y 41.2% corresponde al estado de Jalisco. El parteaguas de la cuenca tiene su máxima elevación a los 2 670 msnm y el punto de salida referenciado por la estación hidrométrica se encuentra a los 1 723 msnm. La pendiente media de la cuenca es de 11%; el cauce principal tiene un desnivel de 323 m y la cuenca presenta un tiempo de concentración de 21 h, respectivamente. La precipitación media anual es de 659 mm, según las normales climatológicas para el periodo 1981-2010 (SMN, 2014), con un régimen de lluvias que inicia en el mes de junio y termina en octubre, concentrándose en este periodo un 89% del total de las precipitaciones anuales, caracterizadas por ser intensas y de corta duración.

Las presas más importantes dentro de la zona descrita son El Palote y El Barrial. La primera se encuentra en Ciudad de León y su propósito es agua potable y control de avenidas, con una capacidad máxima de 17 Mm³; la segunda se ubica sobre San Francisco del Rincón, diseñada para el control de avenidas y riego, con una capacidad de 55.26 Mm³. Otras presas que se destacan son Santa Efigenia, con capacidad de 42.75 Mm³; Jalpa Vieja, con 14.38 Mm³; Ciénaga de Galvanes, con 11 Mm³, y Potrerillos, con 15 Mm³; todas con doble propósito de riego y control de avenidas (Conagua, 2014b).

 

Información climatológica

La información de precipitación para alimentar el modelo de pronóstico se obtuvo de la base de datos del CLICOM (SMN, 2014), utilizando las series de los años 2003 y 2004 a nivel diario, por tener el mayor registro de información completa para la cuenca. En el cuadro 1 se muestran un total de 11 estaciones meteorológicas distribuidas sobre toda la superficie de la cuenca del río Turbio.

 

Información hidrométrica

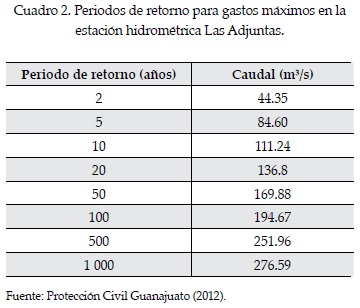
Los caudales medios diarios se obtuvieron de la base de datos del Banco Nacional de Aguas Superficiales, BANDAS (Conagua, 2014a), para la serie de los años 2003 y 2004. En el cuadro 2 se resumen los cuantiles para los gastos máximos registrados en la estación hidrométrica Las Adjuntas, según la Comisión Nacional de Agua y reportados por Protección Civil Guanajuato (2012).

 

Metodología

Los modelos autorregresivos han sido ampliamente usados en la hidrología y los recursos hídricos desde inicios la década de 1960, para la modelación anual y periódica en series de tiempo de tipo hidrológico. La aplicación de estos modelos ha sido atractiva en la hidrología, principalmente porque la forma autorregresiva tiene dependencia del tiempo y por la facilidad para su implementación (Salas et al., 1980; Box et al., 2013).

Se propuso la creación de un modelo autorregresivo con entrada exógena ARX para predecir los caudales medios con base en los registros de series pasadas, obtenidos a partir de la base de datos BANDAS (Conagua, 2014a) para la estación hidrométrica Las Adjuntas. El modelo ARX relaciona las entradas con las salidas del sistema mediante una ecuación lineal en diferencias con coeficientes constantes (Hsu, Moradkhani, & Sorooshian, 2009):

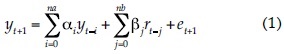
Donde y_t y r_t son el caudal observado y la lluvia en el tiempo t, el cual representa un día; e_t+1 es el término de error en la estimación del caudal; α_i y β_j son parámetros, respectivamente. Los índices na y nb especifican el número de observaciones previas de caudales y lluvias. Es lo que sería un modelo autorregresivo ARX (nα, nb).

Conocida la estructura general del modelo ARX, la formulación en espacio de estados se convierte en una herramienta útil para utilizar el Filtro de Kalman en cualquiera de sus versiones. La ecuación (1) puede representarse en forma de espacio de estados como sigue:

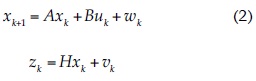
donde x_k+1 es el caudal presente (no observado) de tamaño (n x 1); A es la matriz de parámetros α_i, de tamaño (n x n); x_k, el caudal en el tiempo k de tamaño (n x 1); B, la matriz de parámetros exógenos β_j de tamaño (n x m); u_k representa el vector que contiene la precipitación media registrada en la cuenca para el tiempo k de tamaño (m x 1); z_k, el caudal medido en el tiempo k de tamaño (m x 1); H, la matriz de transformación que mapea el vector de estados al dominio de la medición con dimensiones (m x n); w_k y v_k son vectores que representan el ruido gaussiano en el proceso y el ruido en la medición para cada observación con tamaños (m x 1), de tal manera que:

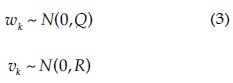
Para el caso específico de la matriz R de covarianza de la perturbación de la medición, ésta se definió de acuerdo con lo reportado por Moralez-Velázquez et al., 2014. La matriz fue representada como α*q_(k-1), donde α es una constante de proporcionalidad que representa un error constante e igual a una fracción del caudal en el tiempo anterior (k - 1). El valor de α en todos los casos tuvo un 5% con respecto al caudal inmediatamente anterior; ese 5% es el error que se cree comete la persona que mide los caudales, es decir, el aforador. De acuerdo con la formulación de la ecuación (2), la dinámica de un sistema permite una representación más sencilla, proporcionando descripciones estadísticas del comportamiento del sistema (Gelb, 1974).

Los modelos en espacio de estados son esencialmente una notación conveniente para abordar el manejo de un amplio rango de modelos de series de tiempo. En la estimación y control de problemas, esta metodología se basa en modelos estocásticos, dado el supuesto de la naturaleza errónea de las mediciones (Ramírez, 2003).

Finalmente, se puede observar que el sistema representado en la ecuación (2) consiste de un componente determinístico y un componente estocástico que reflejan incertidumbre en el modelo (Lee & Singh, 1998).

De la ecuación (3), Q y R pueden cambiar en el tiempo, pero por lo general se suponen constantes por simplicidad (Simon, 2001) y sus valores esperados se pueden representar como se sigue:

De esta forma, el modelo ARX se representa en espacio de estados, facilitando la aplicación del Filtro de Kalman para obtener los pronósticos de caudal en el tiempo (k + 1) a partir de la serie de caudales registrada en el tiempo (k), incluyendo la precipitación media diaria en la cuenca como el componente de entrada exógeno al modelo y siguiendo el esquema del algoritmo representado en la figura 2 mediante estimadores de estados (Kim, 2011).

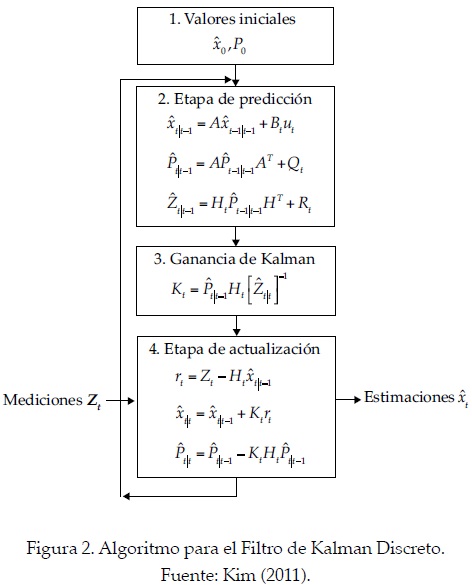
Para crear el modelo ARX se programó una rutina en Matlab^®, utilizando el toolbox de identificación de sistemas para obtener el orden del proceso autorregresivo según el número de términos representados en la ecuación (1).

Teniendo en cuenta que los parámetros estimados por el modelo ARX pueden variar en función de las épocas de mayor precipitación y/o de las variaciones abruptas en los caudales, se estableció un periodo (P) a modo de calibración ("warming up") para estimar los parámetros e iniciar el pronóstico de caudales en el tiempo (t₀ + P).

Una vez definida la longitud del periodo, los pronósticos se realizaron desde (t₀ + P) hasta el tiempo (t₀ + 2P), recalculando los parámetros del modelo ARX para el periodo (2P), iniciando de nuevo el pronóstico ahora desde (t₀ + 2P) hasta (t₀ + 3P) y así de modo sucesivo, tal como se describe en la figura 3. De esta manera, la implementación del ARX+DKF se hizo dinámica y con matrices de estado, que fueron variando en cada periodo definido, disminuyendo el ruido generado en el proceso representado como w_k en la ecuación (2):

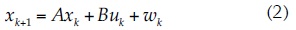
Con el propósito de encontrar diferencias entre los pronósticos para L pasos hacia adelante, es decir, con 24, 48, 72 y 96 horas de anticipación, fue ejecutada una rutina en Matlab^® que utilizó información del estado en el tiempo (k) para avanzar, sin actualizar L pasos en la línea de tiempo. Una vez llegada a la posición L deseada, se realizó la actualización del primer estado pronosticado, como se describe en la figura 4. El ciclo se realizó teniendo en cuenta los periodos de calibración de modelo ARX descritos en la Figura 3.

Para evaluar el ajuste de los pronósticos realizados con respecto a los datos medidos se calcularon las principales estadísticas según Gupta, Kling, Yilmanz y Martínez (2009) para la metodología descrita anteriormente. El error cuadrático medio MSE (Mood, Graybill, & Boes, 1974) y su normalización relacionada, y la eficiencia de Nash-Sutcliffe (Nash & Sutcliffe, 1970) fueron los dos criterios a tener en cuenta, por ser los más utilizados para la calibración y evaluación de modelos hidrológicos con los datos observados.

Además se determinó un intervalo de predicción al 95% de probabilidad para cada serie pronosticada según Chatfield (2004). Con el objetivo de comprobar los supuestos de la teoría general del Filtro de Kalman, se realizaron ajustes a funciones de distribución de probabilidad para los errores e_k = x_k - _k provenientes de las series evaluadas.

 

Resultados y discusión

El modelo ARX que presentó un mejor ajuste para los años 2003 y 2004 fue aquel de un orden autorregresivo de 2 para caudales (nα = 2) y de 1 para precipitación (nb = 1); dichos ajustes se muestran en los cuadro 3 y 4, respectivamente. Se puede observar en ambos cuadros que el modelo mencionado presenta un mejor ajuste, considerando los coeficientes de Nash-Sutcliffe, en especial para pronóstico en 24 horas que, como se verá más adelante, ese pronóstico de 24 horas es el que exhibe un mejor ajuste en el Filtro de Kalman Discreto. Asimismo, siempre es deseable que el modelo no sólo presente el mejor ajuste, sino que también sea con el mínimo de términos posibles, pues resulta más fácil de manejar.

A continuación se muestran los resultados obtenidos para el pronóstico de caudales en la cuenca del río Turbio, implementando el modelo ARX+DKF con información del año 2003. El periodo que utilizó el modelo para su calibración previa y pronósticos posteriores para el año 2003 fue de 20 días. En lo que respecta al periodo de calibración elegido fue el que mejor resultados en términos estadísticos arrojó en el ARX+DKF y dichos estadísticos se mostrarán después.

La figura 5 muestra el pronóstico de caudales obtenidos para L = 1 o con 24 h de anticipación. En la figura 5 se puede notar que hay una diferencia en la escala del tiempo de cuando se presenta la precipitación máxima y el caudal máximo, en especial el evento máximo del mes de septiembre del 2003; quizás esto se pueda deber a la presencia de varias presas en la cuenca del río Turbio. Sin embargo, en el evento máximo de julio del 2003, aunque la precipitación fue mayor que la de septiembre de 2003, el caudal máximo es menor que el de septiembre, quizás esto se deba a las condiciones de humedad antecedente en los suelos de la cuenca que tiene un mes de julio a un mes de septiembre. Algo semejante se observará más adelante en la figura 10, que corresponde al pronóstico del año 2004. En trabajos posteriores se pudiera plantear un Filtro de Kalman en que una variable externa adicional a considerar sea la humedad antecedente, medida como la lluvia en cinco días anteriores, como es el caso de la técnica del número de curva de escurrimiento para calcular los escurrimientos (McCuen, 2005).

De igual forma se realizaron los pronósticos para diferentes pasos hacia adelante L = 2 o 48 h, L = 3 o 72 h, y L = 4 o 96 h de anticipación, respectivamente, con el objetivo de cuantificar los errores de predicción, teniendo en cuenta el esquema descrito en la figura 4.

En el cuadro 5 se resumen las estadísticas para los diferentes pronósticos en el tiempo utilizando los datos de la serie del año 2003.

Los mejores resultados son los pronósticos de caudales realizados un paso hacia adelante, es decir, para aquellos con 24 h de anticipación que los pronósticos realizados con 48, 72 y 96 horas de anticipación.

Según el resumen estadístico del cuadro 5, la media para los caudales pronosticados tiende a preservarse con respecto a la serie de los caudales observados; el coeficiente de eficiencia de Nash-Sutcliffe disminuye conforme el RMSE aumenta a medida que el pronóstico se hace L pasos hacia adelante, generando pérdida de confiabilidad en los pronósticos realizados. Los resultados obtenidos por el PBE para todos los pronósticos en el tiempo indican que los caudales tienden a ser subestimados por el modelo. Los obtenidos presentan un comportamiento característico para caudales bajos, medios y altos de acuerdo con la dispersión que presentan a lo largo de la línea a 45 grados en la figura 6. Por esta razón, los datos se agruparon en tres clases: Q < 20 m³/s, 20 m³/s ≤ Q ≤ 60 m³/s y Q > 60 m³/s (ver figura 7), siguiendo el patrón de dispersión de la figura 6.

El orden para los diagramas de dispersión en la figura 7 son L = 1 gráficas (a, b, c); L = 2 gráficas (d, e, f); L = 3 gráficas (g, h, i), y para L = 4 gráficas (j, k, l). Se puede apreciar que para la serie del año 2003 (ver cuadro 6), el ARX+DKF realizó los mejores pronósticos para el rango de caudales menores a 20 m³/s en términos de RMSE y Nash-Sutcliffe para L = 1 y L = 2 ver gráficas (a,d).

En el mismo rango, los pronósticos para L = 3 y L = 4 no presentan los mejores resultados de acuerdo con los estadísticos evaluados. Por el contrario, para el pronóstico de caudales en el rango de 20-60 m3/s (ver gráficas b, e, h, k de la figura 7), el ARX+DKF tiende subestimar los caudales pronosticados, siendo mayor este índice para los caudales pronosticados por arriba de los 60 m3/s (ver gráficas c, f, i, l de la figura 7).

Como se había descrito antes, la teoría asume que los errores de pronóstico e = (x - ) provienen de una distribución normal. En este sentido, el supuesto fue verificado para los errores obtenidos en las series pronosticadas a 24, 48, 72 y 96 horas de anticipación.

En la figura 8 se presentan los ajustes obtenidos para los errores de pronóstico, teniendo en cuenta los diferentes pasos en el tiempo. En términos generales, todos los errores se ajustan a una distribución t de student escalada.

Según Chatfield(2001), en la práctica los errores no siempre se ajustan a una distribución normal debido a la asimetría que se puede presentar, la presencia de datos atípicos que generan distribuciones con colas pesadas y por errores asociados a los datos involucrados que contaminan la distribución de los errores en la predicción. De acuerdo con lo anterior, se sugiere que el valor para obtener una probabilidad dada se seleccione con base en la distribución para la cual los datos se han ajustado mediante sus parámetros.

Con el objetivo de establecer el grado de incertidumbre asociado con realizar los pronósticos para diferentes pasos en el tiempo, se determinaron los intervalos de predicción para cada valor puntual siguiendo los criterios establecidos por Chatfield (2004).

En la figura 9 se presenta el intervalo de predicción al 95% de probabilidad para el pronóstico realizado con 24 h de anticipación utilizando la serie del año 2003. Se puede observar que el pronóstico es aceptable debido a que la mayoría de los caudales observados están dentro del rango de los intervalos calculados a lo largo de la serie, a diferencia de los intervalos obtenidos en el evento ocurrido entre Sep/08/2003 y Sep/15/2003, donde los caudales observados quedan por fuera del rango calculado, guardando relación con los datos que fueron agrupados en la figura 7 para la clase Q > 60 m³/s con L = 1.

La figura 10 presenta el pronóstico de caudales realizado para la serie del año 2004 utilizando el ARX+DKF para 24 horas de anticipación.

En esta serie pronosticada, el periodo que mejor se ajustó fue de 36 días, considerando en dos el orden autorregresivo para caudales y en uno el número de días de precipitación, como ya se había mostrado anteriormente en el cuadro 4. Las estadísticas para el pronóstico de la serie 2004 se resumen en el cuadro 7.

Los mejores resultados obtenidos fueron para los caudales pronosticados para L = 1 o con 24 horas de anticipación de acuerdo con las estadísticas reportadas en el cuadro 7.

La media de la serie pronosticada para L = 1 tiende a alejarse relativamente en cuanto a la serie de datos observados y a las series pronosticadas con L = 2, L = 3 y L = 4, respectivamente.

En términos generales, a medida que se avanza en el tiempo, el pronóstico tiende a perder eficiencia reflejado en los valores de Nash-Sutcliffe, MSE y RMSE, con la tendencia a subestimar los datos según los valores reportados por el PBE.

Se agruparon los caudales pronosticados para la serie del año 2004, siguiendo la misma estructura con la que se realizó para los datos pronosticados en la serie del año 2003. En este caso, los rangos fueron para los Q < 20 m³/s y Q ≥ 20 m³/s de acuerdo con la dispersión de los datos obtenidos en la figura 11.

En la figura 12 se presentan los resultados para L = 1 gráficas (a, b), para L = 2 gráficas (c, d), para L = 3 gráficas (e, f) y para L = 4 gráficas (g, h). Se observa que los mejores ajustes se encuentran para los caudales menores a 20 m³/s, tal como se observó en la serie del año 2003 (ver gráficas a, c, e, g).

Se puede observar en las gráficas (b, d, f, h) de la figura 12, que los pronósticos para Q ≥ 20 m³/s en todos los pasos del tiempo tienden a perder confiabilidad según el grado de dispersión con respecto a los valores observados, reflejados por el aumento del RMSE y disminución del coeficiente de Nash-Sutcliffea medida que se hace el pronóstico con mayor tiempo de anticipación, tal como se reporta en los estadísticos del cuadro 8.

Al igual que en los resultados obtenidos en la serie del año 2003, los errores de pronóstico se ajustaron a una distribución t student escalada para los diferentes pasos en el tiempo, generada por la presencia de datos atípicos, discutidos anteriormente.

Según el ajuste de los errores presentado en la figura 13, se calculó el intervalo de predicción al 95% de probabilidad con los datos para L = 1 o 24 h de anticipación. Se obtuvieron ajustes satisfactorios con respecto a los valores observados (ver figura 14) en la mayoría de los intervalos calculados, a diferencia de los pronósticos realizados entre oct/01/2004 y oct/04/2004 para los cuales los intervalos no incluyeron los valores observados en el mismo periodo de tiempo, estableciendo una relación de semejanza con los datos agrupados en el rango de Q ≥ 20 m³/s y con 24 h de anticipación reportados en la figura 12.

Kim, Tachikawa y Takara (2004) hicieron la implementación del Filtro de Kalman con el modelo CDRMV3 para el pronóstico de caudales y encontró que los mejores resultados pertenecían a los pronósticos realizados a una hora que para los obtenidos a 12 horas después, evaluados en términos de RMSE.

Por otra parte, Hirpa et al. (2013) encontraron que en términos de Nash-Sutcliffe, los mejores resultados fueron para los pronósticos de caudales realizados para un día que para aquellos que fueron realizados con 15 días de anticipación, en el río Ganges y Brahmaputra de Asia meridional.

En este trabajo se llevó a cabo el pronóstico de caudales para los años 2003 y 2004 porque eran los datos más completos y de más calidad, en la base de datos BANDAS, para alimentar el modelo de Filtro de Kalman. En trabajos posteriores se pudiera probar el Filtro de Kalman en cuencas con datos de caudales más completos; quizás intentar el acceso a la base de datos de caudales de la Comisión Federal de Electricidad (CFE). Sin embargo, el acceso a la base de datos de caudales de CFE no es libre, tal como ocurre con la base de datos BANDAS de la Comisión Nacional del Agua.

 

Conclusiones

El pronóstico de caudales mediante el modelo ARX+DKF en la cuenca del río Turbio para los años 2003 y 2004 fue implementado de manera satisfactoria. Con base en los resultados obtenidos, los pronósticos realizados un paso hacia adelante L = 1 o con 24 horas de anticipación, presentan un mejor ajuste en términos de Nash-Sutcliffe, MSE y RMSE, que los pronósticos realizados a 2, 3 y 4 pasos hacia adelante, es decir, con 48, 72 y 96 horas de anticipación.

Los periodos previos de calibración para la metodología del modelo ARX+DKF son fundamentales para mejorar los pronósticos a través del tiempo, pues la función de respuesta en la cuenca puede ser variante según los periodos del ciclo hidrológico o debido a la presencia de eventos meteorológicos de consideración.

Los errores de pronóstico para las dos series evaluadas no se ajustaron a una distribución normal como teóricamente debería presentarse, pero la presencia de datos atípicos atribuidos a la calidad de la información involucrada genera distribuciones de colas pesadas pertenecientes a la familia de la distribución t de student.

La implementación de técnicas, como el Filtro de Kalman, para el pronóstico de caudales en cuencas con instrumentación muy pobre o deficiente puede ser una tarea compleja si la medición de caudales no es continua o es inexistente, o los registros son de mala calidad y corta duración. De hecho, por eso en este trabajo la implementación del Filtro de Kalman en la cuenca del río Turbio sólo se hizo para los años 2003 y 2004.

En trabajos posteriores se pudiera hacer lo siguiente: (a) considerar la humedad antecedente como variable exógena en el Filtro de Kalman; (b) aplicar el Filtro de Kalman en cuencas instrumentadas por la CFE, en donde la continuidad y la calidad de registros pudiera ser más completa que los registros de BANDAS.

 

Referencias

Abaza, M., Anctil, F., Fortin, V., & Turcotte, R. (2014). Sequential Streamflow Assimilation for Short-Term Hydrological Ensemble Forecasting. Journal of Hydrology, 519, 2692-2706.         [ Links ]

Box, G. E., Jenkins, G. M., & Reinsel, G. C. (2013). Time Series Analysis: Forecasting and Control (746 pp) (4th edition). New Jersey: John Wiley & Sons.         [ Links ]

Chatfield, C. (2001). Prediction Intervals for Time-Series Forecasting (475-494 pp). In Principles of Forecasting. Philadelphia, USA: Springer US.         [ Links ]

Chatfield, C. (2004). The Analysis of Time Series: An Introduction (313 pp) (6th edition). Florida: Chapman & Hall/CRC Press.         [ Links ]

Conagua (2014a). Banco Nacional de Aguas Superficiales, BANDAS. México, DF: Comisión Nacional del Agua. Recuperado de ftp://ftp.conagua.gob.mx/bandas/bases_datos_bandas.         [ Links ]

Conagua (2014b). Sistema de Seguridad de Presas. México, DF: Comisión Nacional del Agua Recuperado de: http://www.conagua.gob.mx/atlas/.         [ Links ]

Gelb, A. (1974). Applied Optimal Estimation. Massachusetts: MIT Press. (374 pp).         [ Links ]

Gupta, H. V., Kling, H., Yilmaz, K., & Martinez, G. F. (2009). Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. Journal of Hydrology, 377, 80-91.         [ Links ]

Hsu, K. L., Moradkhani, H., & Sorooshian, S. (2009). A Sequential Bayesian Approach for Hydrologic Model Selection and Prediction. Water Resources Research, 45(12)., 1-15. W00B12, doi:10.1029/2008WR006824.         [ Links ]

Hirpa, F. A., Hopson, T. M., De Groeve, T., Brakenridge, G. R., Gebremichael, M., & Restrepo, P. J. (2013). Upstream Satellite Remote Sensing for River Discharge Forecasting: Application to Major Rivers in South Asia. Remote Sensing of Environment, 131, 140-151.         [ Links ]

IPCC (2007). Cambio climático 2007: Informe de síntesis (104 pp.). R. K. Pachauri & A. Reisinger (directores de la publicación). Contribución de los Grupos de Trabajo I, II y III al Cuarto Informe de Evaluación del Grupo Intergubernamental de Expertos sobre el Cambio Climático. Ginebra: IPCC.         [ Links ]

Kalman, R. E. (1960). A New Approach to Linear Filtering and Prediction Problems. Journal of Fluids Engineering, 82(1), 35-45.         [ Links ]

Kim, P. (2011). Kalman Filter for Beginners: with Matlab Examples (232 pp.). Seoul, Korea: CreateSpace.         [ Links ]

Kim, S., Tachikawa, Y., & Takara, K. (2004). Embedding Kalman Filter into a Distributed Hydrological Model (pp. 2125). IHP Conference (with WSUD), Adelaide, Australia, November, 21-26.         [ Links ]

Lee, Y. H., & Singh, V. (1998). Application of the Kalman Filter to the Nash Model. Hydrological Processes, 12(5), 755-767.         [ Links ]

Li, Y., Ryu, D., Western, A. W., & Wang, Q. J. (2015). Assimilation of Stream Discharge for Flood Forecasting: Updating a Semidistributed Model with an Integrated Data Assimilation Scheme. Water Resources Research, 51(5), 3238-3258. doi: 10.1002/2014WR016667.         [ Links ]

Liu, J., Wang, J., Pan, S., Tang, K., Li, C., & Han, D. (2015). A Real-Time Flood Forecasting System with Dual Updating of the NWP Rainfall and the River Flow. Natural Hazards, 77(2), 1161-1182.         [ Links ]

Liu, Y., Weerts, A. H., Clark, M., Hendricks-Franssen, H. J., Kumar, S., Moradkhani, H., & Restrepo, P. (2012). Advancing Data Assimilation in Operational Hydrologic Forecasting: Progresses, Challenges, and Emerging Opportunities. Hydrology and Earth System Sciences, 16(10), 105-119.         [ Links ]

Lü, H., Hou, T., Horton, R., Zhu, Y., Chen, X., Jia, Y., Wang, W. & Fu, X. (2013). The Streamflow Estimation Using the Xinanjiang Rainfall Runoff Model and Dual State-Parameter Estimation Method. Journal of Hydrology, 480, 102-114.         [ Links ]

Matlab^® R2013b. MathWorks, Inc.

McCuen, R. H. (2005). Hydrologic Analysis and Design (859 pp) (3rd edition). Upper Saddle, USA: Prentice Hall PTR.         [ Links ]

Mendoza, V. M., Villanueva, E. E., Garduño, R., Nava, Y., Santisteban, G., Mendoza, A. S., Oda B., & Adem, J. (2009). Thermo-Hydrological Modelling of the Climate Change Effect on Water Availability in Two Hydrologic Regions of Mexico. International Journal of Climatology, 29, 1131-1153.         [ Links ]

Montero-Martínez, M. J., Ojeda-Bustamante, W., Santana-Sepúlveda, J. S., Prieto-González, R., & Lobato-Sánchez, R. (abril-junio, 2013). Sistema de consulta de proyecciones regionalizadas de cambio climático para México. Tecnología y Ciencias del Agua, 4(2), 113-128.         [ Links ]

Moradkhani, H., DeChant, C. M., & Sorooshian, S. (2012). Evolution of Ensemble Data Assimilation for Uncertainty Quantification Using the Particle Filter-Markov Chain Monte Carlo Method. Water Resources Research, 48(12), 1-13. 41:W05012, doi: 10.1029/2004WR003604.         [ Links ]

Moradkhani, H., Sorooshian, S., Gupta, H. V., & Houser, P. R. (2005). Dual State-Parameter Estimation of Hydrological Models Using Ensemble Kalman Filter. Advances in Water Resources, 28(2), 135-147.         [ Links ]

Mood, A., Graybill, F., & Boes, D. (1974). Introduction to the Theory of Statistics (229 pp) (3rd edition). Singapore: McGraw-Hill.         [ Links ]

Morales-Velázquez, M. I., Aparicio, J., & Valdés, J. B. (2014). Pronóstico de avenidas utilizando el Filtro de Kalman Discreto. Tecnología y Ciencias del Agua, 5(2), 85-110.         [ Links ]

Nash, J. E., & Sutcliffe, J. V. (1970). River Flow Forecasting through Conceptual Models Part I. A Discussion of Principles. Journal of Hydrology, 10, 282-290.         [ Links ]

Perevochtchikova, M. (2013). Retos de la información del agua en México para una mejor gestión. Realidad, Datos y Espacio. Revista Internacional de Estadística y Geografía, 4(1), 42-57.         [ Links ]

Protección Civil Guanajuato (2012). Recuperado de: http://proteccioncivil.guanajuato.gob.mx/atlas/hidrometeorologico/hidro_cuenca_turbio.php.

Ramírez, Á. S. (2003). El Filtro de Kalman. Nota técnica. Banco Central de Costa Rica, División Económica, Departamento de Investigaciones Económicas.         [ Links ]

Salas, J. D., Delleur, J. W., Yevjevich, V., & Lane, W. L. (1980). Applied Modeling of Hydrologic Time Series (484 pp). Colorado, USA: Highlands, Co., Water Resources Publications.         [ Links ]

Samuel, J., Coulibaly, P., Dumedah, G., & Moradkhani, H. (2014). Assessing Model State and Forecasts Variation in Hydrologic Data Assimilation. Journal of Hydrology, 513, 127-141.         [ Links ]

SMN (2014). Sistema de Información Climática Computarizada CLICOM. México, DF: Servicio Meteorológico Nacional.         [ Links ]

Simon, D. (2001). Kalman filtering. Embedded Systems Programming, 14(6), 72-79.         [ Links ]

Shi, Y., Davis, K. J., Zhang, F., Duffy, C. J., & Yu, X. (2014). Parameter Estimation of a Physically Based Land Surface Hydrologic Model Using the Ensemble Kalman Filter: A Synthetic Experiment. Water Resources Research, 50(1), 706—724.         [ Links ]

Valdés, J. B., Mejía-Velázquez, J. M., & Rodríguez-Iturbe, I. (1980). Filtros de Kalman en la hidrología: predicción de descargas fluviales para la operación óptima de embalses. Informe Técnico No. 80-2. Caracas: Universidad Simón Bolívar, Decanato de Estudios de Posgrado, Posgrado en Planificación e Ingeniería de Recursos Hídricos.         [ Links ]

Welch, G., & Bishop, G. (2006). An Introduction to the Kalman Filter. Chapel Hill: University of North Carolina at Chapel Hill.         [ Links ]

WMO (2009). WMO Report No 168. Guide to hydrological practices volume II: Management of water resources and application of hydrological practices. Geneva: World Meteorological Organization.         [ Links ]

Xie, X., & Zhang, D. (2010). Data Assimilation for Distributed Hydrological Catchment Modeling Via Ensemble Kalman Filter. Advances in Water Resources, 33(6), 678-690.         [ Links ]

Yucel, I., Onen, A., Yilmaz, K. K., & Gochis, D. J. (2015). Calibration and Evaluation of a Flood Forecasting System: Utility of Numerical Weather Prediction Model, Data Assimilation and Satellite-Based Rainfall. Journal of Hydrology, 523, 49-66.         [ Links ]