Artículos técnicos

 

Flujo inducido por el rompimiento de una presa: análisis mediante modelación numérica

 

Flow Caused by Dam Breaks: Numerical Modeling Analysis

 

Ignacio Sabat, Oscar Link*
Universidad de Concepción, Chile
*Autor de correspondencia

Bernd Ettmer
Hochschule Magdeburg-Stendal, Alemania

 

Dirección institucional de los autores

M.C. Ignacio Sabat

Departamento de Ingeniería Civil
Universidad de Concepción
Edmundo Larenas s/n
Concepción, Chile
Teléfono: +56 (41) 2204 320
Fax: +56 (41) 2207 089
nacho.sabat@gmail.com

Dr. Oscar Link

Profesor asociado
Departamento de Ingeniería Civil
Universidad de Concepción
Edmundo Larenas s/n
Concepción, Chile
Teléfono: +56 (41) 2204 320
Fax: +56 (41) 2207 089
olink@udec.cl

Dr. Bernd Ettmer

Professor Fachbereich Wasser und Wasserwirtschaft
Hochschule Magdeburg-Stendal
Magdeburg-Stendal
Breitscheidstr. 2
39114 Magdeburg, Germany
Teléfono: +49 (0) (391) 886 4429
Fax: +49 (0) (391) 886 4430
bernd.ettmer@hs-magdeburg.de

 

Recibido: 24/09/12
Aceptado: 5/06/14

 

Resumen

Se aplica el método de los volúmenes finitos para dar solución a las ecuaciones de Saint Venant 2D con términos fuente que gobiernan el escurrimiento de aguas someras, a fin de calcular el flujo inducido por el rompimiento de una presa. El modelo se verifica mediante el cálculo de siete casos con solución conocida, que son: (1) establecimiento del flujo normal a partir de una superficie libre horizontal; (2) establecimiento del flujo gradualmente variado en un canal con cambio de rugosidad; (3) escurrimiento sobre un obstáculo; (4) formación del salto hidráulico oblicuo; (5) oscilación amortiguada de la superficie libre en un estanque parabólico; (6) escurrimiento inducido por el rompimiento de una presa circular, y (7) escurrimiento inducido por el rompimiento parcial de una presa. El modelo se aplica para simular el flujo inducido por el rompimiento instantáneo de presas, a fin de analizar el efecto de la configuración geométrica del conjunto presa, embalse, valle y cauce sobre el hidrograma de salida. Se simularon 28 escenarios, considerando un valle con sección parabólica y un cauce con sección trapezoidal, donde se varió la altura y orientación del muro de la presa, el ancho de la brecha, la pendiente longitudinal y la rugosidad del cauce aguas abajo. Los resultados obtenidos muestran que la altura de la presa es la variable más influyente en el caudal máximo del hidrograma de salida y que el ancho de la brecha tiene un efecto importante en rompimientos parciales. La rugosidad del lecho atenúa de forma considerable el caudal máximo hacia aguas abajo y aumenta el tiempo de crecida. La orientación del muro y la pendiente longitudinal tienen un efecto menor sobre las crecidas provocadas por rompimiento. El modelo desarrollado predice de manera adecuada el complejo comportamiento que exhibe el flujo inducido por el rompimiento instantáneo de una presa, constituyendo una herramienta de simulación con capacidad predictiva.

Palabras clave: rompimiento de presas, ecuaciones de Saint Venant 2D, hidráulica computacional, esquemas de shock.

 

Abstract

The finite volumes method is applied to solve 2D Saint Venant equations with source terms that determine runoff of shallow water, in order to calculate flows caused by dam breaks. The model is verified by calculating six cases with known solutions: (1) establishing normal flow based on a horizontal free surface; (2) establishing flow that is gradually varied in a channel with changes in roughness; (3) runoff over an obstacle; (4) formation of an oblique hydraulic jump; (5) damped oscillation of a free surface in a parabolic section; (6) runoff from the breaking of a circular dam and (7) runoff from the partial breaking of a dam. The model is applied to simulate the flow caused by the instantaneous breaking of dams in order to analyze the effect of the joint geometric configuration of the dam, reservoir, valley and channel on the outflow hydrograph. A total of 28 scenarios were simulated for a valley with a parabolic section and a channel with a trapezoidal section, in which the height and position of the dam wall were varied as well as the gap width, length of the slope and roughness of the channel downstream. The results obtained show that the height of the dam is the variable that has the largest effect on the peak flow of the outflow hydrograph and the gap width has a large effect on partial breaks. The roughness of the bed considerably mitigates the peak flow downstream and increases flood time. The position of the mural and the length of the slope have a smaller effect on floods caused by dam breaks. The model developed adequately predicts the complex behavior of the flow caused by the instant breaking of a dam and is therefore a simulation tool with predictive capabilities.

Keywords: Dam break, Saint Venant 2D equations, computational hydraulics, shock capturing conditions.

 

Introducción

El rompimiento de presas es un tema relevante en ingeniería hidráulica debido a la alta probabilidad de ocurrencia de consecuencias catastróficas que provoca el flujo inducido aguas abajo del muro. Singh (1996) registró cerca de mil casos de rompimientos de presa sucedidos desde el siglo XII, de los cuales cerca de 200 se registraron en el siglo XX. Muchos rompimientos se encuentran bien documentados en la literatura especializada, como el de las presas Malpasset (Hervouet & Petitjean, 1999), St. Francis (Begnudelli & Sanders, 2007), Tous (Alcrudo & Mulet, 2007) y Gleno (Pilotti, Maranzoni, Tomirotti, & Valerio, 2011). Singh (1996), y Vischer y Hager (1998) indican que las principales causas de rompimiento de presas han sido problemas en las cimentaciones (ca., 37%) y overtopping (ca., 30%). Dada la relevancia del problema, muchos países exigen hoy día como parte del proyecto de un embalse, el análisis de seguridad de la presa, que incluye el cálculo del flujo inducido por su eventual rompimiento.

De manera típica, las presas de tierra y enrocado presentan rompimientos graduales, con una abertura de brecha que demora del orden de horas, y que induce un flujo gradualmente variado hacia aguas abajo, mientras que las presas de hormigón presentan rompimientos instantáneos, con la formación de una onda negativa hacia aguas arriba, controlada por la geometría del valle, y una onda de shock que se propaga hacia aguas abajo (e.g., Vischer & Hager, 1998).

Rubio, Martínez y Meza (2012) estimaron el caudal máximo causado por el rompimiento gradual de una presa aplicando distintas formulaciones empíricas. Realizaron un rastreo de la crecida hacia aguas abajo utilizando el software HEC-RAS, considerando un canal trapezoidal, a fin de establecer la distancia a la que el paso de la avenida ya no representa peligro para la población.

La condición más desfavorable es el rompimiento instantáneo, que puede modelarse mediante las ecuaciones de Saint-Venant, incluyendo los términos fuente que representan el efecto de la pendiente del cauce y de la fricción en el lecho sobre el escurrimiento. Las soluciones analíticas conocidas se limitan al caso 1D para un embalse semi-infinito y canal rectangular aguas abajo de la presa. Dressler (1952, 1954) y Whitham (1955) propusieron soluciones para el rompimiento instantáneo y un canal seco con pendiente horizontal. Hunt (1982, 1984) resolvió el rompimiento instantáneo para un canal seco con pendiente longitudinal; de forma reciente, Chanson (2009) propuso soluciones aplicando el método de las características, para el rompimiento semi-instantáneo de un embalse semi-infinito, con canal rectangular inicialmente seco.

En casos reales, la geometría y resistencia al escurrimiento del valle y del cauce controlan la propagación de las ondas hacia aguas arriba y hacia aguas abajo. Por ello, en la práctica es pertinente una representación 2DH del fenómeno, que se realiza mediante aplicación de métodos numéricos. La existencia de ondas de shock requiere implementar esquemas de discretización espacial con muy baja difusión numérica, que garanticen conservación de los flujos a nivel local y estabilidad de la solución, en especial en la vecindad del shock. La mayoría de estos esquemas se ha propuesto para el problema de Riemann que no considera los términos fuente (e.g., Fraccarollo & Toro, 1995; Brufau & García-Navarro, 2003).

Para la solución de las ecuaciones de Saint-Venant con términos fuente en presencia de ondas de shock, en los últimos años se han desarrollado esquemas de discretización específicos, llamados esquemas de shock, los que, combinados con una adecuada estrategia secado-mojado, presentan una excelente capacidad de simulación del flujo inducido por el rompimiento de una presa. Gottardi y Venutelli (2004) extendieron la formulación del esquema centrado de Kurganov y Tadmor (2000), para la discretización de los términos fuente en las ecuaciones de Saint Venant, presentando resultados favorables en la simulación del rompimiento de presas idealizadas. Zhu, Visser y Vrijling (2004) implementaron un método predictor-corrector basado en el esquema MUSCLE-Hancock (van Leer, 1985) para la simulación de casos de estudio desarrollados en la iniciativa CADAM (Morris, 2001). Soares-Frazão y Zech (2008) presentaron simulaciones numéricas de los efectos del flujo inducido por un rompimiento sobre una ciudad idealizada compuesta por una grilla de 5 x 5 edificios cuadrados, que se orientó a 45 y 90° respecto a la dirección principal de la corriente. Los cálculos se compararon con resultados experimentales, obteniendo una buena concordancia entre ensayos de laboratorio y resultados numéricos. Wang, Liang, Kesserwani y Hall (2011) extendieron la formulación 1D propuesta por Liang y Marche (2009), para simular rompimientos idealizados y también el de la presa Malpasset.

En este artículo se extiende el modelo numérico desarrollado por Link y Donoso (2008) al caso 2D con términos fuente y estrategia secado-mojado. El modelo se verifica mediante el cálculo de siete casos con solución conocida, que son: 1) establecimiento del flujo normal, a partir de una superficie libre horizontal; 2) establecimiento del flujo gradualmente variado en un canal con cambio de rugosidad; 3) escurrimiento sobre un obstáculo; 4) formación del salto hidráulico oblicuo; 5) oscilación amortiguada de la superficie libre en un estanque parabólico; 6) escurrimiento inducido por el rompimiento de una presa circular, y (7) escurrimiento inducido por el rompimiento parcial de una presa. El modelo se aplica para simular el flujo inducido por el rompimiento instantáneo de una presa, a fin de analizar el efecto de la geometría del conjunto presa, embalse, valle y cauce sobre el hidrograma de salida.

 

Metodología

Ecuaciones gobernantes

El sistema de ecuaciones gobernantes corresponde a las ecuaciones de Saint-Venant con términos fuente, que en forma vectorial es:

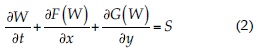
donde W es el vector de variables de flujo; F y G son vectores de flujo que componen la matriz de flujo F en dirección x e y, respectivamente, y S es el vector de términos fuente correspondientes a la pendiente del lecho y la fricción del fondo del cauce. Los vectores W, F, G y S están dados por:

donde h (m) es la profundidad de la columna de agua; u y v (m/s), la velocidad integrada en la vertical en las direcciones de los ejes cartesianos x, y; t (s), el tiempo; g (ms^-2), aceleración de gravedad; x (m), la distancia en sentido longitudinal; y (m) es la distancia en sentido transversal. Las pendientes de fondo S_0x y S_0y (m/m) son:

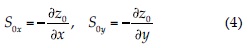
donde z₀ corresponde a la cota batimétrica. La pendiente friccional S_fx y S_fy (m/m) se calcula a partir de la ecuación de Manning como:

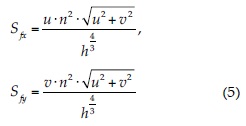
donde n (m^-1/3 s) es el coeficiente de rugosidad de Manning.

 

Formulación discreta del problema

Las ecuaciones gobernantes se llevaron a la forma discreta aplicando el método de los volúmenes finitos, utilizando un esquema descentrado perteneciente a la familia de Q-esquemas, introducida por Harten, Lax y Van Leer (1983), y extendida para las ecuaciones de aguas someras con términos fuente por Bermúdez y Vázquez (1994), y Bermúdez, Dervieux, Desiderii y Vázquez (1998). Integrando la ecuación gobernante se tiene:

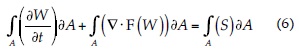
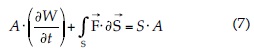
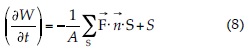
donde A es el área; S, el contorno del volumen de control, y n es un vector normal al contorno. El término de flujo se aproximó mediante la expresión:

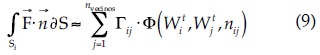
donde Γ_ij (m) es la longitud de la cara entre los volúmenes i y j, y la función Φ se define como:

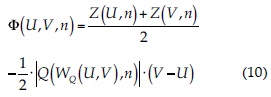
donde:

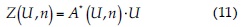
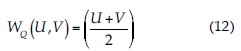
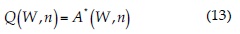
U y V son vectores de propiedades del flujo de volúmenes finitos; n es el vector normal a la cara entre U y V, y A* es la matriz Jacobiana, según Vijayasundaram (1986):

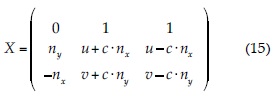
Nótese que 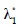,, 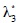(ms^-1) corresponden a los autovalores de A*. Para evitar la indeterminación del problema en las discontinuidades, se introdujo la corrección de entropía de Harten (1984):

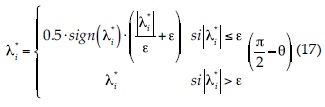
Se consideró e = 10^-5 (m s^-1).

 

Términos fuente

La pendiente de fondo se discretizó como:

donde z_0i y z_0j corresponden a la cota batimétrica del volumen i y su vecino j, respectivamente; d_ij es la distancia entre los centros de los volúmenes; θ_ij, el ángulo generado por la horizontal y la línea que une los centros de los volúmenes i y j, medido en sentido antihorario; A_ij, el área del triángulo formado por el centro del volumen i y los vértices comunes entre los volúmenes i y j, y A_i es la superficie del volumen i. La pendiente friccional se discretizó mediante la ecuación de Manning, como:

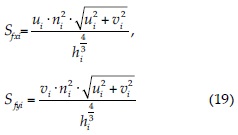
donde u_i y v_i son las componentes de la velocidad en la dirección del eje x e y, respectivamente; h_i es la profundidad de la columna de agua, y n_i corresponde al coeficiente de rugosidad de Manning en el centro del volumen i.

Las derivadas temporales se aproximaron utilizando el esquema explícito de Euler de primer orden, de forma que la solución discreta es:

 

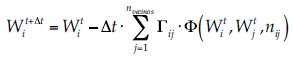
Condiciones de borde

Para el borde abierto se impuso el contorno transmisivo mediante un vecino ficticio con propiedades del flujo idénticas a las del volumen ubicado en el contorno (Toro, 2001):

donde W'_i corresponde al elemento ficticio y W_i al volumen en la frontera del dominio. Para el borde cerrado se impuso el contorno reflectivo, donde la velocidad en la dirección perpendicular a la cara se invierte (Toro, 2001):

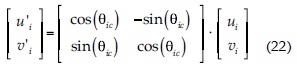
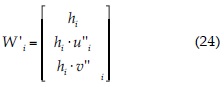
donde h_i, u_i y v_i corresponden a las propiedades del volumen en la frontera del dominio; θ_ic es el ángulo perpendicular a la cara en la frontera y saliente del volumen; u'_i y v'_i son velocidades rotadas en θ_ic, y u''_i y v''_i son las componentes de la velocidad del vecino ficticio en los ejes cartesianos.

 

Estrategia secado/mojado

La estrategia secado/mojado impone la nulidad de los Jacobianos asociados con un volumen seco cuando existen dos vecinos: uno seco y uno mojado. En este caso, las profundidades mínimas se limitan a valores mayores o iguales a cero, y se realiza un balance de masa entre los vecinos mojados, a fin de garantizar la continuidad. Matemáticamente:

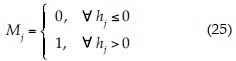
donde M_j indica si el volumen j está seco o mojado y δ_j es la cantidad de masa a balancear. La figura 1 muestra el diagrama de flujo del modelo propuesto.

 

Resultados

Verificación del modelo

La capacidad del modelo desarrollado se verificó mediante siete benchmark test: 1) establecimiento del flujo normal a partir de una superficie libre horizontal; 2) establecimiento del flujo gradualmente variado en un canal con cambio de rugosidad; 3) escurrimiento sobre un obstáculo; 4) formación del salto hidráulico oblicuo; 5) oscilación amortiguada de la superficie libre en un estanque parabólico; 6) escurrimiento inducido por el rompimiento de una presa circular, y 7) escurrimiento inducido por el rompimiento parcial de una presa. Los siete casos mencionados tienen solución conocida y permiten evaluar distintos aspectos del modelo numérico, como la convergencia a estados de equilibrio, conservación, propiedad C de Bermúdez y Vázquez (1994), simulación de discontinuidades en el flujo y modelación del proceso de secado-mojado. Los resultados numéricos se compararon con soluciones analíticas, semi-analíticas o empíricas en forma gráfica, e indicando la diferencia porcentual máxima.

 

Establecimiento del flujo normal a partir de una superficie libre horizontal

Se realizó la simulación del escurrimiento en un canal rectangular de ancho unitario constante de largo igual a 100 m, pendiente igual a 1/2 000 m/m y un coeficiente de Manning igual a 0.02 sm^-1/3. Las condiciones inicial y de borde fueron:

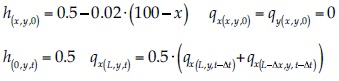
La solución está dada por la ecuación de Manning y es igual a 0.22 m³/s/m. Se utilizó una discretización espacial Δx = 0.25 m y Δy = 0.25 m, y un paso temporal Δt = 0.05 s, con un número de Courant CFL = 0.15. La figura 2 muestra la malla, condición inicial y eje hidráulico calculado. El cuadro 1 muestra la diferencia porcentual máxima entre la profundidad y caudales calculados por el modelo y la ecuación de Manning. Se observa que la predicción del modelo prácticamente coincide con la de Manning.

 

Establecimiento del flujo gradualmente variado en un canal con cambio de rugosidad

Se realizó la simulación del escurrimiento gradualmente variado que causa un cambio de rugosidad en un canal rectangular de ancho unitario constante, de largo igual a 100 m y pendiente igual a 2/1 000 m/m. El canal se dividió en tres tramos de 33.3 m, con rugosidades de Manning iguales a 0.02, 0.04 y 0.02 sm^-1/3, respectivamente. Las condiciones inicial y de borde fueron:

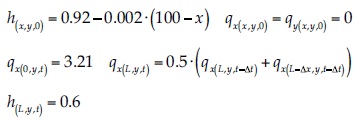
La solución numérica se comparó con aquella calculada por el software HEC-RAS, que resuelve las ecuaciones de Bresse mediante el método del paso estándar. Se utilizó una discretización espacial Δx = 1 m y Δy = 0.4 m, y un paso temporal Δt = 0.10 s, con un número de Courant CFL = 0.14. La figura 3 muestra la malla, condición inicial y eje hidráulico calculado.

Los resultados de la simulación muestran un eje hidráulico semejante al obtenido mediante HEC-RAS. El cuadro 1 muestra la diferencia porcentual máxima entre la profundidad y caudales calculados por el modelo y el HEC-RAS, que no alcanza el 0.5%.

 

Escurrimiento sobre un obstáculo

Se realizó la simulación del escurrimiento sobre un obstáculo con forma de parábola, ubicado en el fondo de un canal rectangular con ancho unitario de 25 m largo, sin pendiente de fondo ni rugosidad. La geometría del obstáculo fue:

Se impusieron tres condiciones iniciales y de borde distintas, a fin de simular: a) el flujo subcrítico sobre un obstáculo; b) el cambio de régimen sub a supercrítico, y c) la formación del salto hidráulico, mostradas en el cuadro 2.

Los resultados numéricos se compararon con la solución analítica publicada por Alcrudo y Benkhaldoun (2001). Se utilizó una discretización espacial Δx = 0.1 m y Δy = 0.1 m, y un paso temporal Δt = 0. 01 s, con un número de Courant CFL = 0.26, 0.32 y 0.38 en los casos a, b y c, respectivamente. La figura 4 muestra la condición inicial y los ejes hidráulicos calculados.

Los resultados de la simulación muestran un eje hidráulico semejante al obtenido mediante Alcrudo y Benkhaldoun (2001). El cuadro 1 muestra la diferencia porcentual máxima entre la profundidad y caudales calculados por el modelo, y la solución de Alcrudo y Benkhaldoun (2001). En el caso a), los errores son muy pequeños, inferiores al 0.5%. En los casos b) y c), la profundidad calculada presenta errores de hasta un 10.87%, lo que se atribuye a las presiones dinámicas que se generan sobre el obstáculo y que el modelo asume como hidrotáticas.

 

Formación del salto hidráulico oblicuo

Se realizó la simulación del escurrimiento en un canal rectangular con 60 m de longitud, 40 m de ancho, sin pendiente ni roce, con una contracción que se inicia 20 m aguas abajo de la entrada, con un ángulo de 8.95°. Las condiciones iniciales y de borde fueron:

Condiciones iniciales

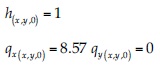
Condiciones de borde

y garantizan un escurrimiento supercrítico antes del angostamiento. La solución numérica se comparó con la solución analítica publicada por Alcrudo y García-Navarro (1993). Se utilizó una discretización espacial Δx = Δy = 0.5 m y un paso temporal Δt = 0.025 s, con un número de Courant CFL = 0.43. En total, se simularon 150 s. La figura 5 muestra la malla de cálculo, condición inicial y superficie libe calculada.

La solución analítica entrega alturas conjugadas iguales a 1.0 y 1.5 m, formando un ángulo de 30° con respecto al eje longitudinal. Se observa que los resultados obtenidos con el modelo propuesto coinciden con dicha solución. El cuadro 1 muestra la diferencia porcentual máxima entre la profundidad calculada por el modelo y la solución analítica de Alcrudo y García-Navarro (1993). El caudal no se compara, ya que éste no se conoce a partir de la solución analítica. Puede notarse que las diferencias no superan el 1.2%.

 

Oscilación de la superficie libre en un recipiente parabólico

Se simuló la oscilación de la superficie libre en un recipiente parabólico de radio superficial igual a 4 500 m. Inicialmente, se impuso una superficie libre inclinada, según Wang et al. (2011):

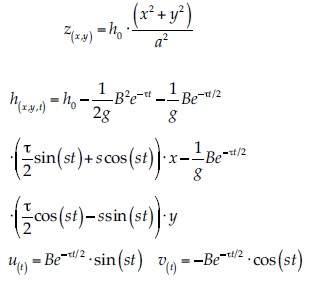
donde:

Se utilizó h₀ = 10 m, a = 3 000 m, B = 5 m/s y τ = 0.002. La solución numérica se comparó con la solución analítica publicada por Wang et al. (2011). Se utilizó una discretización espacial Δx = Δy = 50 m, y un paso temporal Δt = 0.25 s, con un número de Courant CFL = 0.03. En total, se simularon 3 600 s, que abarca tres periodos de la oscilación. La figura 6 muestra la malla de cálculo y condición inicial, velograma en el punto (x, y) = (1 000,0) para ambas componentes u y v, así como la superficie libre calculada para t = 900, 1 800, 2 700 y 3 600 s.

Se observa que el modelo simula de manera adecuada las oscilaciones amortiguadas por efecto de la fricción, y que los resultados coinciden muy bien con la solución analítica de Wang et al. (2011). El velograma calculado para la componente longitudinal de la velocidad coincide con la solución analítica, mientras que para la componente transversal presenta un desfase con la solución analítica que eleva el error máximo. El cuadro 1 muestra la diferencia porcentual máxima entre la profundidad y velocidad calculados por el modelo, y la solución analítica de Wang et al. (2011).

 

Escurrimiento inducido por el rompimiento de una presa circular

Se realizó la simulación del escurrimiento inducido por el rompimiento instantáneo de una presa con 10 m de altura y forma anular. Alrededor de la presa se consideró una planicie de inundación horizontal sin fricción, con profundidad inicial igual a 1.0 m. Las condiciones iniciales y de borde se muestran en el cuadro 3.

La solución numérica se comparó en forma gráfica con los resultados de Mingham y Causon (1998). No existen antecedentes suficientes para comparar valores puntuales ni hacer el cálculo de errores asociados con las simulaciones. Se utilizó una discretización espacial Δx = Δy = 0.25 m y un paso temporal Δt = 0.01 s. En total, se simularon 300 s. La figura 7 muestra la malla de cálculo, condición inicial y superficie libre calculada. Los resultados de la simulación coinciden con la solución numérica de Mingham y Causon (1998).

 

Escurrimiento inducido por el rompimiento parcial de una presa

Se simuló el escurrimiento inducido por el rompimiento instantáneo y asimétrico de una presa orientada en ángulo perpendicular al eje principal del valle, con 200 m de largo, 10 m de ancho y 11 m de altura. La zona de rotura se ubicó entre los 95 y 170 m. Aguas abajo de la presa se modeló una planicie de inundación horizontal sin fricción en dos situaciones: a) inicialmente seca, y b) inicialmente con una profundidad de agua de 5 m. Las condiciones inicial y de borde se muestran en el cuadro 4.

La solución numérica se comparó en forma gráfica con los resultados de Mingham y Causon (1998). No existen antecedentes suficientes para realizar una comparación de valores puntuales ni para llevar a cabo el cálculo del error asociado con las simulaciones. Se utilizó una discretización espacial Δx = 5 m y Δy = 5 m, y un paso temporal Δt = 0.01 s. En total se simularon 150 s. La figura 8 muestra la malla, condición inicial, superficie libre calculada, isolíneas de profundidad y campo de velocidades para las situaciones a) y b), respectivamente. Los resultados de la simulación coinciden con la solución numérica de Mingham y Causon (1998).

 

Análisis del flujo inducido por el rompimiento de una presa

Se analizó el flujo inducido por el rompimiento instantáneo de una presa en un sistema hidráulico idealizado, compuesto por un valle con sección parabólica y un cauce con sección trapezoidal. En todos los casos se consideró que aguas abajo de la presa el canal se encuentra inicialmente seco. La figura 9 muestra esquemáticamente la geometría del sistema hidráulico y la forma típica del hidrograma de salida que causa un rompimiento de la presa.

 

Hidrograma de salida

La figura 10 muestra el caudal máximo del hidrograma de salida en la sección de la presa, calculado con el modelo versus el caudal correspondiente a una onda de gravedad, calculado como:

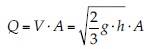
donde h es la profundidad de la presa y A es la sección transversal de la brecha. Se muestran cálculos para profundidades de la presa de 45, 60, 75, 90, 105 y 120 m, y anchos de brecha de 400, 450, 500, 550, 600 y 650 m.

Se observa que existe una relación lineal entre ambos caudales, de manera que el caudal máximo a la salida podría estimarse como Q_máx= 0.41 · Q_onda.

 

Efecto de la brecha, pendiente de fondo, rugosidad y orientación

La figura 11 muestra la variación del caudal máximo de salida correspondiente a la situación base (brecha = 400 m; n = 0.02 sm^-1/3; orientación = 0°) con la brecha, rugosidad del cauce y orientación del muro de la presa respecto al eje longitudinal del valle.

Se observa que la rugosidad y orientación tienen un efecto menor en el caudal máximo del hidrograma de salida. Sin embargo, el caudal máximo crece en forma rápida con el ancho de la brecha hasta que se produce el rompimiento total.

 

Atenuación del hidrograma de salida

La atenuación del hidrograma de salida hacia aguas abajo se estudió mediante la simulación de 28 escenarios, en que se varió la profundidad del embalse, orientación de la presa, ancho de la brecha y pendiente longitudinal respecto al eje longitudinal del valle, a fin de analizar la sensibilidad de la respuesta hidráulica a las propiedades geométricas del sistema. En cada caso se cuantificó el tiempo base y el caudal máximo del hidrograma, en un punto ubicado 2 km aguas abajo de la presa. El cuadro 5 muestra los escenarios analizados y la figura 12 muestra el caudal máximo y tiempo de crecida para dichos escenarios.

Se observa, al igual que en el hidrograma de salida en la sección de la presa, que la variable más sensible fue la profundidad de la presa, que al variar de 45 a 120 m provocó cambios en el caudal máximo de 20 000 a 90 000 m³/s, seguida de la brecha que en el caso de rompimientos parciales puede hacer variar el caudal máximo en un factor tres. La rugosidad del cauce puede disminuir de manera considerable el caudal máximo y aumentar el tiempo de crecida. La pendiente de fondo y orientación tienen un efecto menor sobre el hidrograma y su atenuación hacia aguas abajo.

 

Conclusiones

Se aplicó el método de los volúmenes finitos para dar solución a las ecuaciones de Saint Venant 2D con términos fuente, a fin de calcular el flujo inducido por el rompimiento de una presa.

El modelo se verificó mediante el cálculo de siete casos con solución conocida, que permitieron determinar la capacidad para la simulación de escurrimientos con discontinuidades y simulación del proceso secado/ mojado.

Se analizó el flujo inducido por el rompimiento instantáneo de una presa en un sistema hidráulico idealizado, compuesto por un valle con sección parabólica y un cauce con sección trapezoidal. Se simularon 28 escenarios, donde se varió la altura y orientación del muro de la presa, el ancho de la brecha, la pendiente longitudinal y la rugosidad del cauce aguas abajo. Los resultados muestran que la altura de la presa es la variable más influyente en el caudal máximo del hidrograma de salida y que el ancho de la brecha tiene un efecto importante en rompimientos parciales. La rugosidad del lecho atenúa de manera considerable el caudal máximo hacia aguas abajo y aumenta el tiempo de crecida. La orientación del muro y la pendiente longitudinal tienen un efecto menor sobre las crecidas provocadas por rompimiento.

Los resultados obtenidos pueden aplicarse en la planificación de presas y la gestión del riesgo de inundación ante rompimientos. El modelo desarrollado calculó de forma adecuada el complejo comportamiento que exhibe el flujo inducido por el rompimiento instantáneo de una presa, constituyendo una herramienta de simulación con capacidad predictiva. Como dato de entrada para el modelo desarrollado, casos particulares de graduales, se requiere conocer la forma de la estudio requieren la topografía del cauce y brecha en función del tiempo. planicies de inundación, geometría del muro El desarrollo futuro se orientará a extender y rugosidad. En caso de aberturas de brecha el modelo para simular el escurrimiento en forma acoplada con la evolución del lecho, de manera que se tomen en cuenta efectos del transporte de sedimentos.

 

Agradecimientos

Los autores agradecen a la Comisión Nacional de Investigación Científica y Tecnológica de Chile (Conicyt) y al Servicio Alemán de Intercambio Académico (DAAD), por el financiamiento proporcionado a través del proyecto PCCI2012-027.

 

Referencias

Alcrudo, F., & Benkhaldoun, F. (2001). Exact Solutions to the Riemann Problem of the Shallow Water Equations with a Bottom Step. Computers & Fluids, 30(6), 643-671.         [ Links ]

Alcrudo, F., & García-Navarro, P. (1993). A High-Resolution Godunov-Type Scheme in Finite Volumes for the 2D Shallow-Water Equations. International Journal for Numerical Methods in Fluids, 16(6), 489-505.         [ Links ]

Alcrudo, F., & Mulet, J. (2007). Description of the Tous Dam Break Case Study (Spain). Journal of Hydraulic Research, 45, 45-57.         [ Links ]

Begnudelli, L., & Sanders, B. (2007). Conservative Wetting and Drying Methodology for Quadrilateral Grid Finite-Volume Models. Journal of Hydraulic Engineering, 133(3), 312-322.         [ Links ]

Bermúdez, A., & Vázquez, M. (1994). Upwind Methods for Hyperbolic Conservation Laws with Source Terms. Computers & Fluids, 23, 1049-1071.         [ Links ]

Bermúdez, A., Dervieux, A., Desiderii, J., & Vázquez, M. (1998). Upwind Schemes for the Two-Dimensional Shallow Water Equations with Variable Depth using Unstructured Meshes. Computer Methods in Applied Mechanics and Engineering, 155, 49-72.         [ Links ]

Brufau, P., & García-Navarro, P. (2000). Two-Dimensional Dam Break Flow Simulation. International Journal for Numerical Methods in Fluids, 33, 35-57.         [ Links ]

Chanson, H. (2009). Application of the Method of Characteristics to the Dam Break Problem. Journal of Hydraulic Research, 47(1), 41-47.         [ Links ]

Dressler, R. (1952). Hydraulic Resistance Effect upon the Dam-Break Functions. Journal of Research of the National Bureau of Standars, 49(3), 217-225.         [ Links ]

Dressler, R. (1954). Comparison of Theories and Experiments for the Hydraulic Dam Break Wave. Proc. Int. Assoc. of Scientific Hydrology Assemblée Générale, Rome, 3(38), 319-328.         [ Links ]

Gottardi, G., & Venutelli, M. (2004). Central Scheme for Two-Dimensional Dam-Break Flow Simulation. Advances in Water Resources, 27(3), 259-268.         [ Links ]

Fraccarollo, L., & Toro, E. (1995). Experimental and Numerical Assessment of the Shallow Water Model for Two-Dimensional Dam-Break Type Problems. Journal of Hydraulic Research, 33, 843-864.         [ Links ]

Harten, A. (1984). On a Class of High Resolution TotalVariation-Stable Finite-Difference Schemes. SIAM. J. Numer. Anal., 21(1), 1-23.         [ Links ]

Harten, A., Lax, P., & Van Leer, A. (1983). On Upstream Differencing and Godunov-Type Schemes for Hyperbolic Conservation Laws. SIAM Rev., 25, 35-61.         [ Links ]

Hervouet, J., & Petitjean, A. (1999). Malpasset Dam-Break Revisited with Two-Dimensional Computations. Journal of Hydraulic Research, 37(6), 777-788.         [ Links ]

Hunt, B. (1982). Asymptotic Solution for Dam-Break Problem. Journal of the Hydraulics Division, 108(1), 115-126.         [ Links ]

Hunt, B. (1984). Dam-Break Solution. Journal of Hydraulic Engineering, 110(6), 675-686.         [ Links ]

Kurganov, A., & Tadmor, E. (2000). New High-Resolution Central Schemes for Nonlinear Conservation Laws and Convection-Diffusion Equations. Journal of Computational Physics, 160, 241-282.         [ Links ]

Liang, Q., & Marche, F. (2009). Numerical Resolution of Well Balanced Shallow Water Equations with Complex Source Terms. Advances in Water Resources, 32(6), 873-884.         [ Links ]

Link, O., & Donoso, J. (2008). Development and Verification of a Numerical Model for Calculation of Flow in Open Channels using the Finite Volume Method. Journal of Hydrology and Hydromechanics, 56(3), 190-200.         [ Links ]

Mingham, C., & Causon, D. (1998). High-Resolution Finite-Volume Method for Shallow Water Flows. Journal of Hydraulic Engineering, 124(6), 605-614.         [ Links ]

Morris, M. (2001). CADAM-EU Converted Action on Dam Break Modelling. Recuperado de http://www.hrwallingford.co.uk/projects/CADAM/&.         [ Links ]

Pilotti, M., Maranzoni, A., Tomirotti, M., & Valerio, G. (2011). 1923 Gleno Dam Break: Case Study and Numerical Modeling. Journal of Hydraulic Engineering, 137(4), 480-492.         [ Links ]

Rubio, H., Martínez, E., & Meza, A. (noviembre, 2012). Evaluación de la longitud de peligro por rompimiento de bordos de almacenamiento con capacidad menor a 250.000 m³. Acapulco, Guerrero. XXII Congreso Nacional de Hidráulica.         [ Links ]

Singh, V. (1996). Dam Break Modelling Technology. Dordrecht: Kluver.         [ Links ]

Soares-Frazão, S., & Zech, Y. (2008). Dam-Break Flow through an Idealized City. Journal of Hydraulic Research, 46(5), 648-658.         [ Links ]

Toro, E. (2001). Shock-Capturing Methods for Free-Surface Shallow Flows (third edition). Chichester, UK: John Wiley and Sons Ltd.         [ Links ]

Van Leer, B. (1985). On the Relation between the Upwind-Differencing Schemes of Godunov, Enquist-Osher, and Roe. SIAM (Soc. Ind. Appl. Math.) Journal on Scientific and Statistical Computing, 5, 1-20.         [ Links ]

Vijayasundaram, G. (1986). Transonic Flow Simulations using an Upstream Centered Scheme of Godunov in Finite Elements. Journal of Computational Physics, 63, 416-433.         [ Links ]

Vischer, D., & Hager, W. (1998). Dam Hydraulics. Chichester, UK: John Wiley and Sons Ltd.         [ Links ]

Wang, Y., Liang, Q., Kesserwani, G., & Hall, J. (2011). A 2D Shallow Flow Model for Practical Dam-Break Simulations. Journal of Hydraulic Research, 49(3), 307-316.         [ Links ]

Whitham, G. (1955). The Effects of Hydraulic Resistance in the Dam Break Problem. Proc. R. Soc. Lond., 227, 399-407.         [ Links ]

Zhu, Y., Visser, P., & Vrijling, J. (2004). Review on Embankment Dam Breach Modeling (pp. 1189-1196). In M. Wieland, Q. Ren, and J. S. Y. Tan (Eds.). New Developments in Dam Engineering. London: Taylor & Francis Group.         [ Links ]