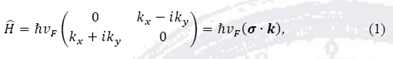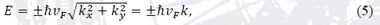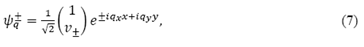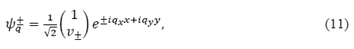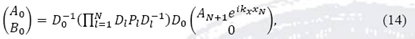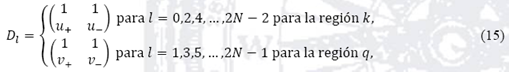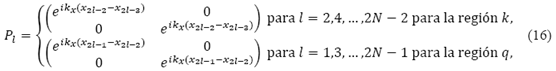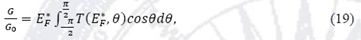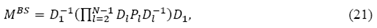Introducción

El grafeno fue descubierto en el año 2004 por investigadores de la Universidad de Manchester, encabezados por los físicos Andre K. Geim y Kostia ^{Novoselov (Novoselov 2004}, 666; ^{Novoselov 2005}, 197). La estabilidad de una monocapa de este material abrió un nuevo camino en el estudio de las propiedades de transmisión y transporte en sistemas bidimensionales. El grafeno es un material bidimensional constituido por una sola capa de átomos de carbono formando una red bidimensional, cuyo espesor es de un único átomo. La estructura cristalina del grafeno consiste en dos subredes triangulares con dos átomos por celda unitaria, esto proviene del hecho de que la red hexagonal original del grafeno no es una red de Bravais. Su estructura de bandas es simétrica con respecto a, E=0 por lo que el salto entre subredes produce la formación de dos bandas de energía y su interacción cerca de los bordes de la zona de Brillouin nos lleva a una relación de dispersión lineal en los puntos K y K', es decir que se conocen como puntos de Dirac.

El grafeno posee propiedades electrónicas relevantes, es un semiconductor con una banda prohibida de energía de tamaño cero, en la cual las cuasipartículas obedecen una relación de dispersión lineal a bajas energías, y que formalmente pueden ser descritas por el hamiltoniano de Dirac,

donde k es el momento de la cuasipartícula, σ son las matrices de Pauli en 2D y v_F es la velocidad de Fermi independiente de k y juega el papel de la velocidad de la luz. Por lo tanto, la ecuación tipo Dirac es consecuencia directa de la simetría cristalina del grafeno, y más aún las cuasipartículas en el grafeno deben de ser descritas por la ecuación de Dirac para fermiones sin masa. Esto nos lleva a tomar como camino la electrodinámica cuántica (^{Katsnelson 2007}, 3) para medir y describir algunos efectos relativistas y encontrar más propiedades electrónicas del grafeno, tales como efecto Hall cuántico anómalo, conductividad mínima y el efecto Klein (^{Zhang 2005}, 201; Katsnelson 2006, 620).

El efecto Klein (^{Katsnelson 2006}, 620), fenómeno relativista en el cual una partícula puede atravesar cualquier barrera de energía potencial sin importar su ancho o su altura, se ha observado en muchas investigaciones y muchos científicos recurren a él para explicar fenómenos encontrados en sus mediciones. Una observación importante es la aparición de oscilaciones en mediciones de conductancia para barreras electrostáticas en grafeno (^{Bai 2007}, 075430, ^{Young 2009}, 222, ^{Rodríguez-Vargas, 2012}, 073711). Este fenómeno presentado en las propiedades de transporte se ha encontrado no sólo en casos para una barrera de potencial, sino que se ha observado en casos donde el caso se extiende a un número finito de barreras y pozos de potencial, tanto así que en la actualidad se hacen investigaciones sobre las propiedades de transporte de los portadores de carga en superredes de grafeno, ya sea tanto en monocapas o bicapas de grafeno (Bai 2007, 075430, ^{Briones-Torres 2014}, 98, ^{Barbier 2009}, 155402, ^{Sinha 2011}, 155439).

Los pioneros en el tema de las superredes fueron Esaki y Tsu, en la década de los setenta, marcaron el inicio del desarrollo de nuevas estructuras artificiales periódicas y su aplicación a nuevos dispositivos (^{Esaki 1970}, 61, ^{Tsu, 1973}, 562). Una superred es un compuesto artificial en donde se depositan películas de dos o más materiales formando una estructura periódica, la mayoría de sus propiedades dependen en gran parte del espesor de los materiales y de su interacción entre sí. Entre las propiedades que presentan tales estructuras se encuentran las oscilaciones de Bloch, el tunelaje resonante, la localización de Winnier-Stark, efectos exitónicos y transporte de minibandas, muchas de las cuales están relacionadas con la estructura de minibandas (^{Esaki 1970}, 61, ^{Tsu, 1973}, 562, ^{Grahn 1995}).

Recientemente, el grafeno ha sido objeto de investigación especialmente por las propiedades únicas que presenta. Una de las tareas es observar que sucede con tales propiedades al aplicar una modulación periódica, especialmente en sistemas multicapas de una, dos o más barreras. Las propiedades de transporte de materiales semiconductores y de las estructuras formadas por ellos son tan importantes para la creación de dispositivos electrónicos más eficientes, y en el grafeno se han encontrado diferencias en tales propiedades respecto a lo encontrado en semiconductores convencionales. Una de las más importantes es que la conductividad puede ser controlada cambiando los parámetros principales del sistema, como el potencial de las barreras y pozos o el número de períodos. Una de las cosas más relevantes encontradas actualmente es que las propiedades de transporte en los sistemas multicapas presentan ciertas peculiaridades, como lo es el carácter oscilante de la conductancia. En uno de nuestros trabajos publicados recientemente encontramos que tal carácter oscilante de una superred periódica puede ser explicado con el uso de la estructura electrónica, encontrando que existe una conexión directa entre los picos de conductancia y la apertura -cierre de las minibandas de energía (^{Briones-Torres 2014}, 98).

Con base a lo anterior, la razón del presente trabajo es encontrar que sucede con la conductancia utilizando una superred tipo sinusoidal y si de igual manera podemos encontrar la relación entre los picos de conductancia y las minibandas de energía. Para eso consideraremos dos tipos de superredes sinusoidales en grafeno, construidas de dos maneras: usando campos electrostáticos y empleando sustratos mixtos. Haremos una comparación de las propiedades de transmisión, transporte y estructura electrónica de ambas superredes, la elección de esto dos sistemas es porque son sistemas opuestos, para el caso electrostático se da la aparición del efecto Klein, lo que no sucede para el caso de sustratos.

Método

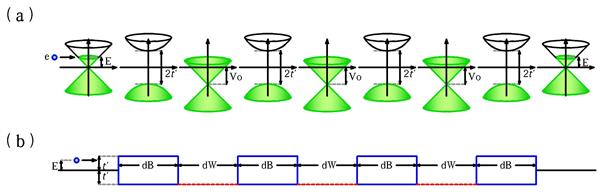
El método de cálculo que usamos es el método de la matriz de transferencia (^{Yeh 2005}), para la propagación de ondas electromagnéticas en medios multicapas, este método puede ser aplicado a electrones de Dirac, con algunas especificaciones particulares que estos acarrean. Para dejar más claro este método, empezaremos por suponer que tenemos un sistema multicapas de Grafeno (SMG) como el mostrado en la Figura 1. Estos sistemas pueden ser formados colocando una sábana de grafeno ya sea sobre un sustrato mixto de SiO₂ y, SiC o bien alternando potenciales electrostáticos.

Figura 1 Diagrama de un sistema multicapas de grafeno con N barreras de potencial, con sus matrices dinámicas y de propagación correspondientes a cada región del sistema. 

Para nuestros cálculos, se han tomado ambas formas de crear un SMG, antes de enunciar formalmente el método de la matriz de transferencia, haremos un breve análisis para encontrar el hamiltoniano y la función de onda para cada SMG (tanto para el formado por un sustrato mixto como para el caso electrostático) (^{Viana 2008}, 325221).

Para el caso de SMG formado por un sustrato mixto, es bien sabido que es posible controlar el tamaño del gap del grafeno modificando la interacción de éste con el sustrato sobre el cual es depositado, que será , SiC o SiO₂. Con esto se logran tener regiones donde el grafeno tendrá gap con un ancho finito y otras donde no tendrá gap, y esto hace posible formar un SMG (^{Zhou 2007}, 770). Entonces tendremos dos regiones, que aparecen periódicamente en el SMG, la región k donde la sábana de grafeno es colocada sobre el sustrato SiO 2, región donde no existe gap en el grafeno y con función de onda, ψ_k y la región q en la cual se deposita la sábana de grafeno y que induce un gap de ancho finito 2t´ (t´es el término de masa, prácticamente es el alto de la barrera), en esta región se tiene una función de onda ψ_q.

Para la región, k los electrones de Dirac poseen un comportamiento relativista, idéntico al de las partículas relativistas con masa cero, entonces el hamiltoniano estará dado por

donde la vF es la velocidad de Fermi de los electrones de Dirac en grafeno, con un valor de, v_F = c/300 que para el caso de sustratos mixtos esta dada por v_F = 3ta/(2ħ),donde t se define como el factor de medida de interacción de los átomos carbono-carbono en el grafeno, con un valor de aproximadamente de 2.7 eV, α es la distancia carbono-carbono, que en para grafeno es igual a 1.42, Å las componentes del pseudoespín σ = (σ_x, σ_y ) son las matrices de Pauli y p = (p_x, p_y)es el operador de momento.

Con esto, la solución general a la ecuación de Dirac para la región, k será

donde

con s = sign (E) y, θ =arctan (k_y/k_x ) por lo tanto la energía correspondiente es

que es una relación de dispersión lineal.

Por otro lado, para la región, q como ya existe un gap, los electrones de Dirac ahora tendrán masa y el hamiltoniano será,

donde, t'= mv² _F aquí m juega el papel de la masa efectiva, producto de la apertura del gap generado por el SiC, para nuestros cálculos numéricos t´= 0.13 eV. Entonces la solución general para la ecuación de Dirac en la región q es

donde

por lo tanto la energía correspondiente a esta región está dada por

esta relación de dispersión ya no es lineal sino de tipo parabólico.

Ahora consideraremos el caso donde el SMG es formado por potenciales electrostáticos, el campo electrostático es aplicado perpendicularmente sobre la sábana de grafeno.

El efecto principal al aplicar campos electrostáticos a la sábana de grafeno es la generación de un desplazamiento de los conos de Dirac que es proporcional a la magnitud del campo V ₀. El hamiltoniano para este caso estará dado por

donde V(x) = V ₀ es el potencial unidimensional a lo largo del eje x. Tomando en cuenta la región, q que es donde se induce un gap debido al campo aplicado, la solución general a la ecuación de Dirac será

Donde

con una relación de dispersión dada por

que también es de tipo lineal.

Pasemos ahora al método de la matriz de transferencia, para eso consideremos al SMG de la Figura 1. Coloquemos nuestro origen en, x ₀ = 0 entonces tomando en cuenta la conservación del momento transversal e imponiendo condiciones de continuidad a la función de onda de las diferentes interfases a lo largo de la dirección x se puede obtener la relación entre los coeficientes de las ondas incidentes reflejadas del lado izquierdo con las ondas transmitidas del lado derecho mediante:

sin olvidar que estamos asumiendo que el medio final es igual al medio inicial y que al final de la N-ésima barrera ya no habrá onda reflejada por lo que BN+1 = 0.

En la ecuación (14) las matrices D_l y P_l dentro de la productoria, son las matrices dinámicas y de propagación, respectivamente, correspondientes a cada una de las regiones que forman el sistema multicapas de grafeno, éstas ecuaciones acorde a nuestros resultados anteriores, se definen como

y las matrices de propagación

de la productoria y de las dimensiones de las matrices dinámicas y de propagación podemos definimos la matriz de transferencia de dimensiones 2x2 como

entonces podemos encontrar que la transmitancia de los electrones de Dirac a través del sistema multicapas de grafeno, estará dada como

Por lo tanto vemos que la transmitancia está dada en función del elemento M ₁₁ de la matriz de transferencia, lo que significa que para calcular la transmitancia es necesario conocer el elemento matricial M ₁₁.

La transmitancia nos permite calcular la conductancia en el régimen lineal directamente a través del formalismo de Landauer-Büttiker (^{Datta 1995}),

donde , es la energía de Fermi adimensional, con, y , es el factor fundamental de conductancia, con L_y el ancho del sistema en el eje transversal y, y θ es el ángulo de incidencia de los electrones con respecto al eje x.

Por último, para calcular el espectro de estados acotados, es necesario cambiar de condiciones blandas a duras, es decir los anchos de la primer y última barrera del SMG se extienden hasta el infinito (Pereira 2006, 045424). La condición para tener estados acotados es que el vector de onda de las barreras semi-infinitas sea imaginario puro es decir q_x → iα_x , de aquí resulta una ecuación trascendental entre la energía y el vector de onda transversal de los electrones de Dirac como

luego, utilizando el formalismo de la matriz de transferencia encontraremos que

es la matriz de transferencia correspondiente al caso de estados acotados.

Resultados

Los resultados obtenidos son para dos tipos de superredes con potencial periódico sinusoidal: una superred creada por medio de potenciales electrostáticos (EGSLs, mostrada en la Figura 2) y la otra creada por medio de sustratos (SGSLs, mostrada en la Figura 3). Por medio de la matriz de transferencia se calcularon las propiedades de transmisión, transporte y estructura electrónica, para anchos dw = dB = 50 α, 100 α y 200 α, donde dW es el ancho de pozos y dB el de barreras, α es la distancia carbono-carbono. Usamos los ángulos de incidencia θ= 0 y π/6 y una energía de incidencia de 0.13 eV. Los altos de barrera son de 0.13 eV y para los pozos de -0.13 eV, todo esto a diferente número de barreras NB.

Figura 2 Superred con potencial periódico sinusoidal creada por la aplicación de potenciales electrostáticos. 

Figura 3 Superred con potencial periódico sinusoidal creada por sustratos mixtos. 

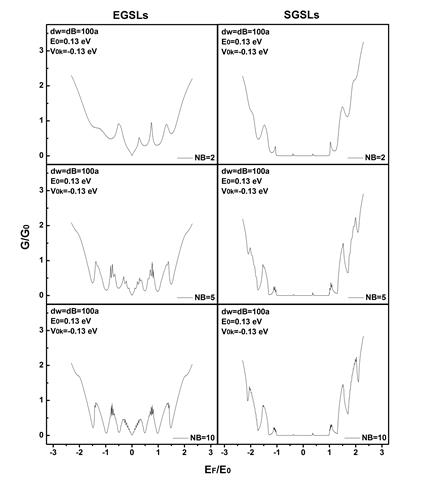
Empezaremos por mostrar los resultados para transmitancia como función de energía, Figura 4. Los parámetros usados son NB = 2, 5 y 10, dw = dB = 100α , y θ = 0 (línea roja) y π/6 (línea negra). Para EGSLs los espectros muestran que para un ángulo de incidencia normal la transmitancia es perfecta, sin importar el número de barreras. Por lo tanto los electrones atraviesan las barreras como si éstas fueran transparentes. Entonces podemos confirmar que el efecto Klein realmente aparece en superredes de este tipo. Sin embargo el caso no es el mismo para SGSLs, pues se puede apreciar que el espectro de transmitancia tanto para incidencia normal como a incidencia oblicua, es rico en estructura, y es notorio que los electrones en este caso sienten la presencia del número de barreras y pozos. Además el efecto Klein no se da en este tipo de superredes. Al aumentar el número de barreras el espectro de transmisión a incidencia oblicua para EGSLs se vuelve simétrico, pues la diferencia entre el número de barreras y pozos es de 1. Caso contrario a SGSLs, donde el número de pozos casi es el doble que de barreras y por lo tanto su espectro de transmisión se vuelve asimétrico. La presencia de huecos es importante para este análisis.

Figura 4 Transmitancia como función de la energía para EGSLs y SGSLs 

Consideramos dos maneras de presentar la conductancia, la primera se muestra en la Figura 5, se variaron los anchos dw y dB, se tomó como fijo el número de barreras NB = 5. Nuevamente la simetría y la asimetría en los espectros con respecto al origen de la energía es evidente para EGSLs y SGSLs respectivamente, pero ahora para el aumento de los anchos. También es apreciable el carácter oscilatorio de la conductancia con el aumento de los anchos. Además existe una gran diferencia entre la conductancia para EGSLs y SGSLs pues conforme aumenta el ancho de las barreras y pozos, la conductancia se mantiene en los mismos órdenes de magnitud para EGSLs. Caso contrario a SGSLs pues la región central de la curva crece con el aumento de los anchos y por lo tanto la conductancia disminuye fuertemente.

Figura 5 Conductancia como función de la energía para EGSLs y SGSLs a diferentes anchos de barreras y pozos. 

En la Figura 6 se muestra la segunda representación de la conductancia, ahora variamos el número de barreras y fijamos el anchos de las barreras y pozos a dw=dB=100α. Se pueden observar cosas similares a las curvas de conductancia mostradas anteriormente, sin embargo lo más interesante es que con el aumento de los anchos el carácter oscilatorio es mucho más evidente.

Figura 6 Conductancia como función de la energía para EGSLs y SGSLs a diferente número de barreras. 

Para una ilustración más explícita de las propiedades de transmisión en los sistemas EGSLs y SGSLs, la Figura 7 muestra los contornos (E,θ ) para anchos fijos dw = dB = 100α, en donde los ejes horizontal y vertical corresponden a la energía y al ángulo de incidencia de los electrones. Como se puede ver la columna de la izquierda muestra los resultados para EGSLs y la columna derecha para SGSLs, la primer fila de resultados es para NB = 2, la segunda para NB = 5, y la última para NB =10.

Figura 7 Diagrama de contorno, ángulo en función de la energía para EGSLs y SGSLs con dw=dB=100α para diferente número de barreras NB = 2, 5 y 10 para la primer, segunda y tercer fila respectivamente. 

Una de las características notables para EGSLs es la simetría de los contornos con respecto del ángulo de incidencia y la asimetría con respecto de la energía. Para SGSLs a simetría permanece con respecto del ángulo de incidencia pero no para la energía. Para analizar la transmitancia los colores rojo y negro corresponden a transmitancia perfecta y nula respectivamente. Para el sistema EGSLs, el caso NB = 2 no presenta resonancias y tampoco zonas con transmitancia nula, sin embargo tales regiones aparecen conforme aumenta el número de barreras. Un resultado notorio se da en la amplitud de la región central para ángulos pequeños, pues ésta se reduce con el aumento del número de barreras pero nunca desaparece, debido a la influencia del efecto Klein y a la preferencia por ángulos pequeños, mostrando así que la conductancia se mantiene. Para el sistema SGSLs, se presentan resultados similares, pero la transmitancia es más sensible al aumento del número de barreras, pues las regiones prohibidas de energía es vuelve más notoria. Las regiones de transmisión perfecta desaparecen con al aumento del número de barreras, lo que lleva a una disminución notable en la conductancia.

La Figura 8, muestra otro contorno (E,θ) , ahora fijamos el número de barreras NB = 5, donde los anchos son dw=dB=50α, para la primera fila, dw=dB=100α para la segunda y dw=dB=200α para la tercera. Nuevamente las simetrías en los contornos mencionadas anteriormente tanto para EGSLs como para SGSLs se mantienen.

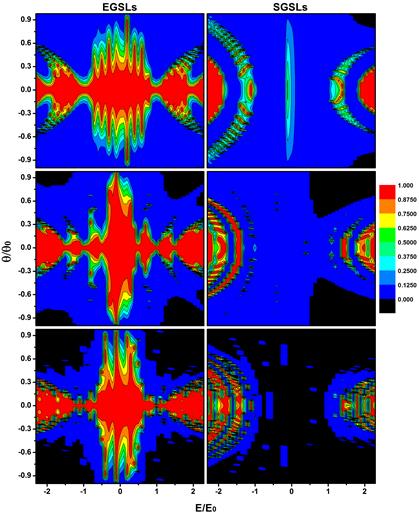
Figura 8 Diagrama de contorno, ángulo en función de la energía para EGSLs y SGSLs con NB = 5y con anchos dw=dB=50α, 100α y 200α para la primer, segunda y tercer fila respectivamente. 

Para el sistema EGSLs, el efecto Klein se hace notar pues la región central a ángulos pequeños jamás desaparece con el aumento de los anchos. Tampoco desaparece la región de transmitancia perfecta (región roja), porque se mantiene prácticamente constante aunque aparezcan regiones de energía prohibida. Por lo tanto la conductancia disminuye muy poco manteniéndose en los mismos órdenes de magnitud.

Para SGSLs, el contorno muestra más estructura para huecos que para electrones, debido al número de barreras existentes para huecos, y como era de esperarse las regiones de transmitancia nula son evidentes incluso a dw=dB=50α. Con el aumento de los anchos tales regiones se vuelven prácticamente más notorias, abarcando gran parte del espectro (el carácter evanescente de las ondas rige en este tipo de estructuras). Junto con ello se presenta una disminución importante en la conductancia. Además la aparición de resonancias es más notable para dw=dB=200α, lo que concuerda con la aparición de oscilaciones en la conductancia.

Para hablar más explícitamente de las propiedades de transporte y explicar las oscilaciones en la conductancia calculamos el espectro de estados acotados, mostrado en la Figura 9. En este caso el gráfico muestra la energía en función del momento transversal. Usamos condiciones duras, por lo tanto ahora en vez de referirnos al número de barreras estaremos usando el número de pozos (Nw), fijándolo en Nw=4, para la primer fila dw=dB=50α, para la segunda dw=dB=100α y para la última fila dw=dB=200α.

Figura 9 Espectro de estados acotados para EGSLs y SGSLs con Nw = 4 y con anchos dw=dB=50α, 100α y 200α para la primer, segunda y tercer fila respectivamente. 

Para el sistema EGSLs la apertura y cierre de minibandas ocurre prácticamente a la misma altura, desapareciendo la región de energía prohibida entre ellas, esto es más notorio si observamos la conductancia en la Figura 5. Por ejemplo para dw=dB= 200α en el valor 1, se puede apreciar un valle de conductancia casi nula pero jamás llega a cero, debido al efecto Klein, y si volvemos al espectro de estados acotados el cierre de la minibanda mostrada antes del valor de 0.13 eV ocurre de manera conjunta con la apertura de la minibanda mostrada después de éste valor. Por lo tanto, cada apertura y cierre de minibanda en el espectro de estados acotados corresponde a un pico principal de conductancia (donde nos referimos a pico principal al formado por un aumento y disminución fuerte). Sin embargo en cada pico principal existen disminuciones y aumentos no tan prominentes en la conductancia correspondientes a la apertura y cierre de cada una de las subbandas que forman la minibanda.

En el caso del sistema SGSLs, las subbandas se degeneran, y al igual que EGSLs la apertura y cierre de las minibandas ocurren a una misma energía con el aumento de los anchos dw=dB. Ahora vayamos a la Figura 5, podemos observar que para dw=dB=50α, existen unos picos muy cercanos al cero de energía, tales picos corresponden las subbandas que aparecen cercanas al cero de energía en el espectro de estados acotados. Enseguida existe una conductancia prácticamente nula, y entre las subbandas existen regiones sin estados acotados. Además nuevamente aparece un pico principal en la conductancia alrededor de 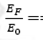1, relacionado con la minibanda degenerada a la altura de la barrera en el espectro de estados acotados.

De igual manera podemos analizar el caso para dw=dB=100α. La minibanda que aparece poco antes del valor de 0.05 eV corresponde con el pico principal en la conductancia aproximadamente en /0,4, enseguida el canal se cierra y se abre la siguiente minibanda aproximadamente al nivel de la altura de la barrera, y nuevamente este caso coincide con los picos en la conductancia y las oscilaciones alrededor de esta energía. Para dw=dB=200α existen unos picos de conductancia que no aparecen antes de 0.13 eV y que para este caso corresponderían a las minibandas observadas en el espectro de estados acotados, pero no aparecen debido a la precisión de nuestros cálculos. Las dos siguientes minibandas después del valor de 0.13 eV si corresponden con los picos principales que surgen después de EFE0=1 .

Por lo tanto, entre las cosas importantes que encontramos es la degeneración de las subbandas para formar minibandas, característica de las superredes, otra es la apertura y cierre de las mismas para explicar la disminución y aumento de la conductancia. Por lo tanto de manera cualitativa el espectro de estados acotados fue necesario para explicar las propiedades de transporte.

Conclusiones

En conclusion, hemos estudiado las propiedades de transmisión, transporte y estructura electrónica en superredes de grafeno, donde hemos considerado superredes con potencial periódico sinusoidal o dicho de otro modo superredes con polaridad alternada. En particular se llevó a cabo un análisis comparativo de superredes creadas por medio de potenciales electrostático (presentan tunelaje Klein) y superredes creadas por medio de sustratos mixtos (no presentan tunelaje Klein). Empleamos el método de matriz de transferencia para el cálculo de las propiedades de transmisión y espectro de estados acotados, mientras que para las propiedades de transporte se utilizó el formalismo de Landauer-Büttiker. Los principales resultados que encontramos, es que las propiedades de transmisión transporte y estructura electrónica pueden ser moduladas fácilmente ajustando los parámetros de la superred. La transmitancia y conductancia en el caso de EGSLs están dominadas por el tunelaje Klein. Para el caso de SGSLs éstas propiedades son muy sensibles al tamaño del sistema debido al carácter evanescente de los electrones. Como parte importante de los resultados las oscilaciones encontradas en la conductancia para ambas superredes EGSLs y SGSLs, pueden ser multiplicadas o reducidas en número modificando el ancho de las barreras y pozos, o reforzadas aumentando el número de barreras en la estructura. La polaridad alternada trae como consecuencia que las propiedades de transmisión y transporte como función de la energía para EGSLs sean simétricas con respecto al origen de la energía mientras que para SGSLs son asimétricas, esto debido a la influencia de huecos en las estructuras. Por último se ha encontrado en investigaciones recientes que los picos en la conductancia obedecen, en el caso de un pozo cuántico en grafeno (Rodríguez-Vargas 073711), a la apertura-cierre (degeneración) de subbandas en el espectro de estados acotados. Sin embargo en nuestros resultados esto se contrasta, pues los picos en la conductancia obedecen la apertura-cierre de minibandas para ambos tipos de superredes, tanto EGSLs como SGSLs. Además la polaridad alternada baja el nivel de energía de las subbandas, las degenera y origina que la apertura-cierre (degeneración) de minibandas sea en el mismo nivel.