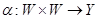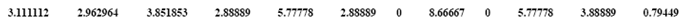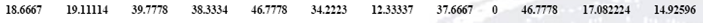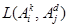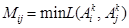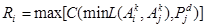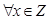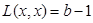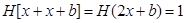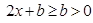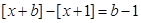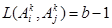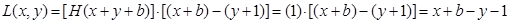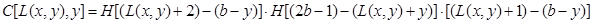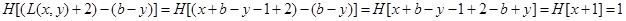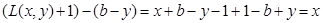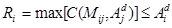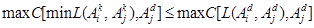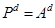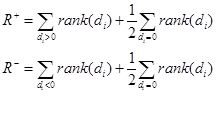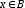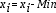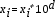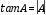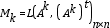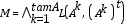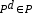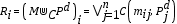text new page (beta)
Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Similars in
SciELO 
Permalink
Introducción
La creación y desarrollo de algoritmos inteligentes tiene relevancia en áreas tales como el Reconocimiento y Clasificación de Patrones, la Minería de Datos y la Inteligencia Computacional (Theodoridis y Koutrombas 2009, 7).
Son cuatro las tareas principales asociadas con los algoritmos inteligentes: recuperación, regresión, clasificación y agrupamiento; las tres primeras tareas se ubican en el paradigma de aprendizaje supervisado, mientras que la última se asocia con el aprendizaje no supervisado (Duda, Hart y Stork 2000, 12).
Dado un algoritmo específico, la base matemática que se incluye en su diseño y operación determina el enfoque al que pertenece. Por ejemplo, hay algoritmos que se basan en el concepto de métrica y en las propiedades de los espacios métricos para hacer la clasificación de los patrones (Cover 1967, 23); de igual manera, han surgido clasificadores basados en el enfoque estadístico-probabilístico, los cuales están basados en el teorema de Bayes (Marques de Sá 2001, 90); y de forma similar, existen clasificadores creados a partir del enfoque neuronal, cuya base conceptual consiste en modelos matemáticos de la neurona del cerebro humano (Du y Swami 2014, 10). Estos son sólo algunos ejemplos de la gran variedad de enfoques que existe para reconocer y clasificar patrones; hay muchos más.
Cada enfoque tiene sus prototipos. Por ejemplo, el Clasificador Bayesiano es el algoritmo más conocido en el enfoque estadístico-probabilístico, mientras que el Perceptrón Multicapa es el prototipo del enfoque neuronal. Al enfoque basado en métricas pertenece uno de los clasificadores más eficaces, no obstante su simplicidad: el clasificador basado en los vecinos más cercanos (k-NN, por k-Nearest Neighbor). Sin embargo, la mayoría de los algoritmos comparten características de más de un enfoque y de otras áreas de la ciencia. Lo anterior es notorio en las máquinas de soporte vectorial (SVM, siglas de Support Vector Machines), en cuyo algoritmo interviene de manera importante el concepto de optimización: las SVM maximizan el margen entre los patrones en el límite de las clases (estos patrones son llamados vectores de soporte) (Cortes y Vapnik 1995, 275).
La propuesta del presente artículo se enfoca en la tarea de clasificación supervisada de patrones; por ello, se asume que se cuenta con un banco de patrones divididos previamente en clases o etiquetas. El modelo aquí propuesto se ubica en el enfoque asociativo de clasificación de patrones (Yáñez Márquez 2002, 30). Al igual como sucede en los demás enfoques, éste también posee una base conceptual que rige el diseño y operación de los algoritmos: aquí, la base conceptual consiste en el establecimiento de asociaciones entre patrones, a través de la aplicación de entes matemáticos específicos para cada algoritmo.
El ente matemático que se ha elegido para el diseño y operación del modelo aquí propuesto, es la función de Heaviside (Abramowitz y Stegun 1972, 1020). Así, en este artículo se propone un nuevo modelo de clasificación de patrones, en modo supervisado, cuyo diseño y operación se basa en la función de Heaviside; este Clasificador de Heaviside es del tipo one shot, lo cual garantiza que el nuevo modelo carecerá de problemas de convergencia.
El resto del artículo está organizado como sigue: en la segunda sección se presenta un resumen conciso del surgimiento y desarrollo del enfoque asociativo de clasificación de patrones, a fin de contextualizar el modelo aquí propuesto. Tomando como base este contenido, en la sección tercera se describe y fundamenta, a través de lemas, teoremas y corolarios, el Clasificador de Heaviside. La cuarta sección, Resultados experimentales, es importante porque da soporte experimental al nuevo modelo, justificando así su inclusión en el estado del arte. Inmediantamente después, se incluye la relevante sección de Discusión y conclusiones, para finalmente cerrar con las Referencias.
Enfoque asociativo del reconocimiento y clasificación de patrones
¿Cuántas veces nos sucede que no podemos recordar la melodía o la letra de una canción de nuestro agrado? Sin embargo, en el mismo instante en que escuchamos un pequeño trozo de la melodía o un fragmento de la letra, somos capaces de recordar la melodía o la letra completas de la canción en cuestión, sin esfuerzo adicional. Similarmente, los seres humanos somos capaces de reconocer el rostro de una persona, no obstante que sólo veamos una parte de la cara, o que la persona se haya puesto peluca o lentes, o se haya quitado la barba o el bigote, por ejemplo.
En relación con este tipo de habilidades, se dice que la mente humana es asociativa (Anderson y Rosenfeld 1990, 271); esto significa que los seres humanos poseemos memoria asociativa, dado que podemos recordar, mediante asociaciones, lo que hemos aprendido. Esto ocurre con objetos, seres vivos, conceptos e ideas abstractas, incluso cuando hay contaminación o alteración (como en el caso de los rostros con lentes o sin barba, o las melodías incompletas).
Algunos grupos de investigación se interesan en crear modelos matemáticos que se comporten como memorias asociativas. Con base en esos modelos, se crean, diseñan y operan sistemas (software o hardware) que sean capaces de aprender y recordar objetos, seres vivos, conceptos e ideas abstractas. Para lograr lo anterior, es preciso representar esos objetos o ideas como patrones, lo cual se realiza usualmente a través de vectores columna de dimensión finita con valores reales, o racionales, o enteros, o booleanos, o mezclas de algunos de ellos (Uriarte-Arcia, López-Yáñez y Yáñez-Márquez 2014, 4).
Típicamente, un modelo asociativo clasificador de patrones consta de dos fases: aprendizaje y clasificación. Si 
es un patrón perteneciente al conjunto de entrenamiento que pertenece a la clase k, la fase de aprendizaje se esquematiza de la siguiente manera (Figura 1):
Cuando el modelo asociativo ha concluido la fase de aprendizaje, ya está listo para clasificar patrones de clase desconocida. Si 
es un patrón cuya clase se desconoce, la fase de clasificación del modelo asociativo se esquematiza así (Figura 2):
El primer modelo matemático de memoria asociativa de que se tiene noticia es la Lernmatrix de Steinbuch, desarrollada en 1961 por el científico alemán Karl Steinbuch (Steinbuch 1961, 39); no obstante la importancia de su modelo y las potenciales aplicaciones, el trabajo pasó casi inadvertido. El siguiente modelo de memoria asociativa surgió 8 años después: en 1969, tres científicos escoceses crearon el Correlograph, el cual es un dispositivo óptico elemental capaz de funcionar como una memoria asociativa. En palabras de los autores "el sistema es tan simple, que podría ser construido en cualquier laboratorio escolar de física elemental" (Willshaw, Buneman y Longuet-Higgins 1969, 961).
El año de 1972 fue testigo de la generación de cuatro nuevos modelos asociativos relevantes. Al inicio del año, James A. Anderson de la UCLA publicó su Interactive Memory (Anderson 1972, 202); en abril, Teuvo Kohonen, profesor de la Helsinki University of Technology, presentó ante el mundo sus Correlation Matrix Memories (Kohonen 1972, 355); tres meses después, Kaoru Nakano de la University of Tokyo, dio a conocer su Associatron (Nakano 1972, 382); y en el ocaso del año, Shun-Ichi Amari, profesor de la University of Tokyo, publicó un trabajo teórico donde continuaba con sus investigaciones sobre las Self-Organizing Nets of Threshold Elements (Amari 1972, 1200). Los trabajos de Anderson y Kohonen, en conjunto, dieron lugar al Linear Associator.
Si 1972 fue el año de los pioneros en el área de las memorias asociativas, 1982 fue el año del científico estadounidense John J. Hopfield. Su artículo de ese año publicado por la National Academy of Sciences, impactó positivamante y trajo a la palestra internacional su modelo asociativo (Hopfield 1982, 2556). La razón es que el modelo Hopfield, que funciona como una red neuronal y también como una memoria asociativa, impulsó de nuevo al área de las redes neuronales, después de sufrir más de una década de estancamiento.
Los trabajos de Hopfield causaron excitación en el mundo de las memorias asociativas y las redes neuronales, y las actividades de investigación en el área se incrementaron. No obstante la cantidad de nuevos modelos propuestos después del éxito de la memoria Hopfield de 1982, no sucedió nada realmente trascendente hasta 1998, cuando aparecieron las memorias asociativas morfológicas (Ritter, Sussner y Diaz-de-Leon 1998, 286). La diferencia fundamental entre estos modelos y las memorias asociativas clásicas como el Linear Associator y la Memoria Hopfield, es que mientras éstas basan su operación en la suma y multiplicación usuales, las memorias morfológicas se basan en las operaciones morfológicas de dilatación y erosión. Los modelos morfológicos rompieron el esquema utilizado a través de los años en los modelos clásicos, que utilizan operaciones convencionales entre vectores y matrices para la fase de aprendizaje, y suma de productos para recuperar patrones.
Las memorias asociativas morfológicas usan máximos o mínimos de sumas para la fase de aprendizaje, y máximos o mínimos de sumas para la fase de recuperación. Con este nuevo esquema, superaron claramente a las memorias asociativas clásicas.
La aparición, desarrollo, aplicaciones y consolidación de las memorias asociativas morfológicas en 1998 marcó un hito en el campo de las memorias asociativas, porque superaron en prácticamente todos los aspectos de interés, de súbito, a los modelos conocidos. Este hecho se convirtió en una fuerte motivación para la creación y desarrollo de las memorias asociativas Alfa-Beta, en México, durante el año 2002 (Yáñez Márquez 2002, 301).
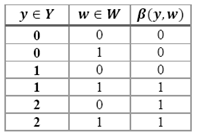
Las memorias asociativas Alfa-Beta constituyen un modelo alternativo a las memorias asociativas morfológicas. Los entes matemáticos que sustentan a los modelos Alfa-Beta incluyen dos operaciones binarias inventadas ex profeso, cuyos operadores fueron bautizados arbitrariamente con las dos primeras grafías del alfabeto griego: Alfa y Beta. Alfa se usa en la fase de aprendizaje, y Beta en la fase de clasificación.
Sean los conjuntos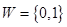 
y 
. Los operadores Alfa(α) y Beta(β) se definen en forma tabular, como se ilustra en las siguientes tablas:
A más de una década de su creación, los modelos Alfa-Beta se han consolidado, y las actividades del Grupo de Investigación Alfa-Beta giran en torno a estos modelos, sus extensiones y sus aplicaciones. El enclave académico del Grupo es el Centro de Investigación en Computación del Instituto Politécnico Nacional, y los nuevos modelos basados en los operadores originales se desarrollan como tesis de doctorado en ciencias de la computación, además de que se generan publicaciones nacionales e internacionales en revistas arbitradas.
Así se han creado, entre otros modelos, las redes neuronales Alfa-Beta sin pesos (Argüelles Cruz 2007, 37), los modelos Alfa-Beta difusos (Sánchez Garfias 2009, 33) y las memorias asociativas Alfa-Beta bidireccionales (Acevedo-Mosqueda, Yáñez-Márquez y López-Yáñez 2007, 25). Tomando como base los operadores Alfa y Beta originales, se creó el Clasificador Gamma, en cuyo algoritmo interviene un código especial diseñado también en el seno del Grupo: el código Johnson-Möbius (López-Yáñez, Argüelles-Cruz, Camacho-Nieto y Yáñez-Márquez 2011, 696).
El advenimiento del algoritmo del Clasificador Gamma abrió una veta muy interesante de nuevas aplicaciones de éste y de algunos algoritmos híbridos Alfa-Beta. Se exploran áreas de aplicación tan disímbolas como la predicción de contaminantes atmosféricos y los componentes de polución arrojados por el escape de un automóvil, procesos de predicción en ingeniería de software, detección de fracturas craneales en radiografías, reconocimiento de conceptos en lattices y reconocimiento de voz emotiva, entre otras.
Recientemente, los modelos asociativos Alfa-Beta han arrojado resultados muy prometedores al realizar predicciones en series de tiempo correspondientes a la producción de pozos petroleros (López Yáñez, Sheremetov y Yáñez Márquez 2014, 25); lo mismo que en el diseño e implementación de sistemas de soporte para la toma de decisiones en el ámbito médico (Aldape-Pérez, Yáñez-Márquez, Camacho-Nieto y Argüelles-Cruz 2012, 289).
El Grupo Alfa-Beta está innovando constantemente. En este contexto, se ha iniciado un conjunto de proyectos y actividades de investigación que involucran la fusión o extensión de los operadores Alfa y Beta con algunas funciones especiales. Es el caso de la función de Heaviside, cuando el primer autor de este artículo se percató de que con esta función era posible representar extensiones de los operadores Alfa y Beta, más allá del sistema binario.
Mediante un proceso inductivo, se procedió a realizar experimentos de aprendizaje y clasificación de patrones en el sistema numérico de base 3, luego en el de base 4 y después en el de base 5. Los resultados fueron buenos, porque en algunos casos el desempeño de los nuevos clasificadores era superior al modelo original en binario.
Acto seguido, el equipo de investigación procedió a generar las expresiones para las fases de aprendizaje y clasificación de patrones, extendido a un sistema numérico de base b, donde b es un entero mayor que 1. A partir de los buenos resultados, se procedió a crear un nuevo modelo clasificador de patrones basado en la función de Heaviside: el Clasificador de Heaviside, cuya descripción y fundamentación matemática, a través de lemas, teoremas y corolarios, se presenta a continuación.
Clasificador de Heaviside
Algunas hipótesis acerca del modelo propuesto
El modelo que se está proponiendo es del tipo one shot, y por ello la clasificación se realiza en un solo paso. Una premisa que subyace al presente trabajo, es que esta característica permitirá superar las limitaciones que exhiben los modelos del estado del arte, los cuales en su mayoría son iterativos.
Hipótesis 1.- Dado que el Clasificador de Heaviside es supervisado, se asume que se tiene acceso a un banco de patrones clasificado previamente en un número finito de clases, al estilo de los que se incluyen en el prestigioso repositorio de la UCI (Lichman,2013).
Hipótesis 2.- Los patrones pueden ser representados como vectores de dimensión finita, cuyas componentes son números reales. Si hay números negativos, es posible aplicar una transformación para obtener sólo componentes reales no negativas. Además, es posible truncar o redondear estos números reales no negativos, a fin de obtener vectores de dimensión finita con componentes racionales no negativas; estos valores se representan mediante números racionales que contienen un número no negativo y un número finito de decimales.
Hipótesis 3.- Es posible encontrar un escalamiento que permita transformar esas componentes racionales con un número finito de decimales, en números enteros no negativos. La tres hipótesis previas permiten transformar el banco de datos original en un banco de vectores de cardinalidad finita y de dimensión finita, cuyas componentes son números enteros no negativos. De aquí se desprende la siguiente, y última, hipótesis.
Hipótesis 4.- Es posible representar cada una de las componentes de los vectores del banco transformado, en términos de un sistema numérico posicional de base b, donde b es un número entero mayor que 1.
Después de aplicar al banco de datos original los procesos operativos involucrados en cada una de las hipótesis previas, se tendrá disponible un banco de vectores con componentes enteras no negativas. La representación simbólica de estas componentes enteras no negativas, se realizará respecto de una base b de algún sistema numérico posicional.
Para ilustrar un poco lo mencionado en las hipótesis anteriores, considérese el siguiente conjunto de patrones, en donde cada fila representa un patrón diferente:
El valor mínimo del patrón 1 es -2.88889, al restar este valor al patrón obtenemos el siguiente patrón transformado:
En el patrón 2 el valor mínimo es -16.6667; al restar este valor de las componentes del patrón se obtiene lo siguiente:
En el patrón 3 el valor mínimo es -22.6667; al restar este valor de las componentes del patrón se obtiene el siguiente patrón transformado:
Finalmente, en el patrón 4 el valor mínimo es -9.11111; al restar este valor del patrón se obtiene el siguiente patrón transformado:
Por lo tanto, el banco de datos transformado queda de la siguiente forma:
Al revisar el banco de datos transformado se obtiene que el máximo número de dígitos decimales que tienen las componentes es de 6, por lo tanto todas las componentes de todos los patrones del banco de datos serán multiplicadas por 106. El banco de datos resultante queda de la siguiente forma:
El banco de datos ha quedado en términos de números enteros no negativos, lo cual satisface las primeras tres hipótesis. A partir de esta representación es posible transformar las componentes, y por lo tanto el banco de datos, en términos de un sistema numérico base b en donde b>1, lo cual satisface la hipótesis 4.
La función de Heaviside y los métodos de validación
Aquí es donde entra de lleno la Función de Heaviside. No obstante que en la literatura de las funciones especiales la Función de Heaviside aparece definida de diversas maneras, en este trabajo se adoptará la definición incluida en una de las referencias más relevantes y respetadas en el área: el Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables de Abramowitz y Stegun (Abramowitz y Stegun 1972, 1020), la cual es avalada por importantes obras como (Bracewell 2000, 61).
Definición 1: Sea x un número real. La Función de Heaviside de x se define mediante la siguiente expresión:
Asumiendo que ya se cuenta con un banco de vectores con componentes enteras no negativas (al que llamaremos B), representadas éstas respecto de una base b de algún sistema numérico posicional, se procede a aplicar un método de validación estándar, tal como hold-out, leave-one-out o k-fold-cross-validation (el cual es implementado normalmente con el parámetro k=10) (Witten y Frank 2011, 152).
De la aplicación de uno de estos métodos de validación de modelos en el banco de vectores B, se obtienen dos conjuntos de patrones, mutuamente exclusivos: el conjunto de aprendizaje (al que se denominará A) y el conjunto de prueba (que se nombrará como P) cuya unión es, precisamente, el conjunto B.
Operaciones originales L y C
Para su funcionamiento, el Clasificador de Heaviside consta de dos operaciones originales: una para la fase de aprendizaje (a la que llamamos L) y otra para la fase de clasificación de patrones (a la que llamamos C).
Considerando que el modelo de esta propuesta trabaja con operaciones propias de las lattices y estructuras algebraicas ordenadas (Blyth 2005, 20), existen dos modos operativos del Clasificador de Heaviside: el modo que corresponde al supremo (HS) y el modo que corresponde al ínfimo (HI).
Mientras que la operación de aprendizaje L es igual para ambos modos, no sucede lo mismo con la operación de clasificación C, la cual varía con cada modo; específicamente, para el modo HI se ocupa sólo uno de los términos de la operación genérica C.
Nota 1: Dado que el modo HS es el dual del modo HI, en este artículo sólo se describe lo concerniente al modo HI; el modo HS se puede obtener por dualidad.
Definición 2: Si
son la i-ésima y la j-ésima componentes del k-ésimo patrón del conjunto A de aprendizaje, respectivamente, y si
son la ij-ésima componente del modelo del Clasificador de Heaviside M y la j-ésima componente del k-ésimo patrón del conjunto P de prueba, respectivamente, el modo operativo HI del Clasificador de Heaviside utiliza las siguientes operaciones de aprendizaje y clasificación de patrones:
Definición 3: Sean
dos patrones que pertenecen al conjunto de aprendizaje A en un Clasificador de Heaviside en modo operativo HI. Se define el producto externo bajo L de ambos patrones, y se denota como
, a una matriz cuya ij-ésima componente se calcula así:
Siendo 
la i-ésima y la j-ésima componentes del k-ésimo y d-ésimo patrón del conjunto A de aprendizaje, respectivamente.
Nota 2: Si la dimensión de los patrones de A es n, entonces el producto externo bajo L es una matriz de dimensiones nxn.
Nota 3: Es posible que k=d.
Fases de aprendizaje y clasificación de patrones
Definición 4: Fase de Aprendizaje. La ij-ésima componente del modelo del Clasificador de Heaviside M, en modo operativo HI dado un conjunto de aprendizaje A, se define por la siguiente expresión:
Nota 4: El valor mínimo se toma con respecto al índice k, que va de 1 a card(A).
Definición 5: Fase de Clasificación. Sea M un Clasificador de Heaviside en modo operativo HI, y sea
un patrón del conjunto de prueba P de dimensión n; la clase que se le asigna a este patrón es la clase del patrón que se recupera al realizar la siguiente operación con la que se obtiene la i-ésima componente del patrón recuperado R:
Nota 5: El valor máximo se toma con respecto al índice j, que va de 1 a n.
Nota 6: Por definiciones 4 y 5, se tiene:
Fundamentación teórica del Clasificador de Heaviside
Con base en las definiciones previas, se diseñaron y se demostraron los lemas, teoremas y corolarios que describen teóricamente el funcionamiento del Clasificador de Heaviside, sus alcances y sus limitaciones.
Teorema 1.- Sea
tal que
, entonces
tal que
se cumple
.
Demostración:
Por hipótesis y por la definición 1 se tiene:
, dado que 
Y además se cumple que: 
Al realizar las operaciones, resulta lo siguiente:
q.e.d.
Corolario 1.1:
Sea tal que . Si 
entonces 
Demostración:
Dado que se cumple la hipótesis del Teorema 1, éste se puede aplicar directamente, haciendo x=0:
q.e.d.
Corolario 1.2:
Sea tal que . Entonces 
Demostración:
Dado que se cumple la hipótesis del Teorema 1, éste se puede aplicar directamente, haciendo x=b-1:
q.e.d.
Lema 1.- Un Clasificador de Heaviside M en modo operativo HI contiene sólo valores b-1 en su diagonal principal.
Demostración:
De acuerdo con la definición 4, las entradas de la diagonal principal de M se calculan con la siguiente expresión:
Pero por el Teorema 1, el valor de 
es constante y no depende del índice k; por ello, se tiene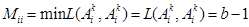 
para todo valor de i.
q.e.d.
Lema 2.- Sea
tales que
. Entonces se cumple la siguiente expresión:
.
Demostración:
Por definición 2:
Por otro lado:
Sustituyendo en la expresión de C:
q.e.d.
Lema 3.- Sea M un Clasificador de Heaviside en modo operativo HI, y sea
un patrón del conjunto de aprendizaje A, entonces:
Demostración:
Por definición 4, se tiene que:
Pero es claro que para cualquier valor fijo d del índice k se cumple la siguiente desigualdad:
Aplicando la operación C con 
en ambos lados de la desigualdad y tomando el máximo con respecto al índice j:
Por nota 6, se tiene que si 
:
Y por transitividad con la expresión previa:
Por Lema 2, se tiene el resultado, porque max es con respecto al índice j, no al i:
q.e.d.
Lema 4.- Sea M un Clasificador de Heaviside en modo operativo HI, y sea un patrón del conjunto de aprendizaje A, entonces:
Demostración:
Al hacer j=i en la expresión 
se tiene:
Pero por Lema 1, para cualquier valor de k (incluyendo d) se tiene:
Por lo que:
Y finalmente, por Lema 2:
q.e.d.
Teorema 2.- Un Clasificador de Heaviside M en modo operativo HI, clasifica correctamente cualquier patrón
Demostración:
Por Lemas 3 y 4, para un valor de índice de patrón fijo d, se cumplen simultáneamente estas dos desigualdades: y para todos los valores del índice i, el cual representa la dimensión de los patrones de aprendizaje.
Las dos desigualdades simultáneas equivalen a la igualdad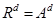 
, por lo que el patrón recuperado es precisamente , lo cual significa que se le asigna su propia clase; es decir, es clasificado correctamente.
q.e.d.
En el teorema 2 el índice d se fijó arbitrariamente, por lo que la conclusión es válida para cualquier patrón del conjunto de aprendizaje A.
De aquí surge una conclusión MUY RELEVANTE, en relación con el funcionamiento del Calsificador de Heaviside en modo operativo HI: EL CLASIFICADOR DE HEAVISIDE EN MODO OPERATIVO HI CLASIFICA CORRECTAMENTE TODOS LOS PATRONES DEL CONJUNTO DE APRENDIZAJE.
¿Por qué es tan relevante esta conclusión? Por la sencilla razón de que, entre la miríada de algoritmos inteligentes para clasificación de patrones que existen en el estado del arte, sólo una mínima cantidad de ellos clasifican correctamente todo el conjunto de aprendizaje.
Para el modo operativo HS del Clasificador de Heaviside, es posible demostrar un teorema similar, lo que potencia fuertemente las bondades y alcances del nuevo modelo.
Pero este Clasificador también posee limitaciones, como cualquier obra del quehacer humano, en los ámbitos cotidiano, artístico, educativo, industrial o científico: por ejemplo, ¿qué ocurre si el conjunto de aprendizaje A contiene patrones con diferentes dimensiones? Pues ocurre que al tomar los máximos sobre el índice j de la dimensión, las operaciones fallarían rotundamente y los teoremas 1 y 2 no se cumplirían.
Una manera adecuada, además del método basado en la teoría matemática, de visualizar los alcances y limitaciones de este modelo, es la realización de experimentos con patrones extraídos de la realidad cotidiana del quehacer humano, en sus diferentes ámbitos.
Resultados experimentales
Se hizo un estudio comparativo entre el modelo de clasificación propuesto contra nueve clasificadores reconocidos en el estado del arte del Reconocimiento de Patrones, los modelos comparados fueron los siguientes:
Memorias Morfológicas Min (Ritter, Sussner, y Diaz-de-Leon, 1998, p. 285) (este modelo de memorias asociativas se basa en las dos operaciones básicas de la morfología matemática),
Clasificador 1NN (Cover y Hart, 1967, p. 21) (este clasificador asigna a los patrones de prueba la clase del vecino más cercano a partir de una función de distancia),
K-NN con K=3 (Duda, Hart, y Stork, 2001, p. 177) (este modelo asigna a los patrones de prueba la clase mayoritaria entre sus tres vecinos más cercanos, en caso de tener un empate la clase será asignada de forma aleatoria),
Naïve Bayes (Duda, Hart y Stork, 2001, p. 52) (este modelo de clasificación está basado en la teoría de la probabilidad, se asigna la clase que sea considerada como la más probable a partir del patrón de entrada),
Perceptrón Multicapa (Rumelhart, Hinton, y Williams, 1986, p. 533) (uno de los modelos de redes neuronales feedforward más conocidos en donde se utiliza el algoritmo de entrenamiento conocido como backpropagation),
Máquinas de Soporte Vectorial (Cortes y Vapnik, 1995, p. 274)(técnica muy popular desarrollada por Vapnik hace dos décadas que busca establecer el margen óptimo entre dos clases),
SMO (Platt, 1998, p. 44) (Sequential Minimal Optimization: modelo empleado para resolver el problema de la programación cuadrática durante el entrenamiento de máquinas de soporte vectorial),
Redes Neuronales de Base Radial (Broomhead y Lowe, 1988, p. 326) (tipo especial de redes neuronales que utilizan funciones de base radial como funciones de activación),
Función Logística (Tatsuoka, 1985, p. 55) (modelo de regresión logística multinomial).
Para realizar la comparación entre el clasificador de Heaviside y los clasificadores enlistados anteriormente, se eligió el uso de una técnica estadística no paramétrica denominada Test de Wilcoxon. A continuación se presentan algunas de las características principales de esta prueba.
Prueba no paramétrica de Wilcoxon
El Test de Wilcoxon (Wilcoxon, 1945, p. 80) se utiliza para comparar diferencias de medias en dos muestras relacionadas. Sin embargo, un caso particular de esta problemática es la comparación de los resultados de la ejecución de dos algoritmos sobre el mismo conjunto de bancos de datos. El test determina, dentro de un intervalo de confianza, si se acepta o no se acepta la hipótesis de igualdad de medias. Si no se acepta, se puede decir que existen diferencias significativas entre los algoritmos a comparar (Derrac, García, Molina, y Herrera, 2011, p. 6). El test consiste en lo siguiente:
Sea 
la diferencia del desempeño de dos algoritmos en alguno de n posibles problemas, dichas diferencias son evaluadas de acuerdo con sus valores absolutos. Sea 
la suma de los rankings o rangos en los cuales el desempeño del primer algoritmo es mayor al desempeño del segundo y sea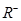 
la suma de los rangos en los cuales el segundo algoritmo tiene mejores resultados que el primero; los rangos correspondientes para 
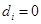se dividen uniformemente entre las sumas, se ignorará uno de los rangos en caso de que la cantidad de sumas sea impar. Las sumas y 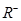se calculan de la siguiente forma:
Sea T la menor de las sumas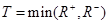 
, si T es menor que la distribución de Wilcoxon para n grados de libertad (Zar, 1998, p. 165), la hipótesis nula de igualdad es rechazada y por lo tanto un algoritmo dado es significativamente diferente que el otro con un valor p asociado.
Para considerar como válido el resultado de la prueba de Wilcoxon es importante tomar en cuenta que los valores de significancia estadística deben estar entre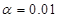 
y 
; el valor 
permite establecer un intervalo de confianza entre el 90% y 99%, típicamente 95%. Si el valor de la probabilidad arrojado (p) es menor que alfa, se dice que se rechaza la hipótesis nula (porque cae en la zona de rechazo del test), y por ende se acepta la hipótesis alternativa (que es la que plantea que sí hay diferencias).
La prueba de Wilcoxon asume la conmensurabilidad de las diferencias, pero sólo de forma cualitativa: es decir, las diferencias grandes entre los desempeños cuentan más; sin embargo, las magnitudes absolutas siguen siendo ignoradas. Desde el punto de vista estadístico, la prueba es más segura dado que no asume la distribución normal, además de que no se ve afectada por la presencia de outliers, o patrones atípicos (Derrac et al., 2011, p. 7).
Para cumplir con la cantidad mínima de comparaciones u observaciones requeridas por las pruebas de Wilcoxon, se eligieron los siguientes bancos de datos, algunos de los cuales fueron tomados del repositorio UCI (Lichman, 2013), y otros más fueron extraídos del repositorio KEEL (Alcalá-Fernandez et al., 2011, p. 256):
Appendicitis (Datos de pacientes para estimar si padece apendicitis o no),
Australian (banco de datos relacionado con solicitudes para tarjetas de crédito).
Banana (banco de datos formado a partir de objetos agrupados en grupos con forma de banana).
Bupa (banco de datos que analiza desórdenes en el hígado),
Cleveland (banco de datos relacionado con enfermedades cardiacas),
Columna Vertebral (banco de datos de características biomecánicas para determinar posibles problemas en la columna vertebral),
Glass (banco de datos para la clasificación de seis tipos de vidrio que pueden ser hallados en una escena de crimen ),
Haberman (datos de un estudio que se realizó a pacientes que siguen con vida después de una cirugía para cáncer de mama),
Heart (detecta la presencia o ausencia de males cardiacos).
Ionosphere: (determinar si una señal transmitida es buena o mala).
Iris Plant (el mundialmente conocido banco de datos de la Iris Plant el cual contiene mediciones de tres tipos diferentes de plantes de Iris),
Magic (simular el registro de partículas gamma en un telescopio a partir de un conjunto de imágenes).
New Thyroid (banco de datos utilizado en la clasificación de pacientes normales, que padecen hipotiroidismo o que padecen hipertiroidismo),
Phoneme (banco de datos para distinguir los sonidos nasales y orales).
Pima Indians Diabetes (banco de datos relacionados con la incidencia de la diabetes en mujeres jóvenes de la tribu indígena de los Pima),
Ring (banco de datos artificial, propone una distribución multivariada de patrones).
Segment-Test (Banco de datos utilizado en la determinación de regiones en imágenes digitales),
Unbalanced (Una versión desbalanceada de un banco de datos que describe formas de vehículos),
Wine (banco de datos relacionado con el reconocimiento de tres tipos diferentes de vinos),
Winsconsin (Banco de datos relacionado con el diagnóstico del cáncer de mama).
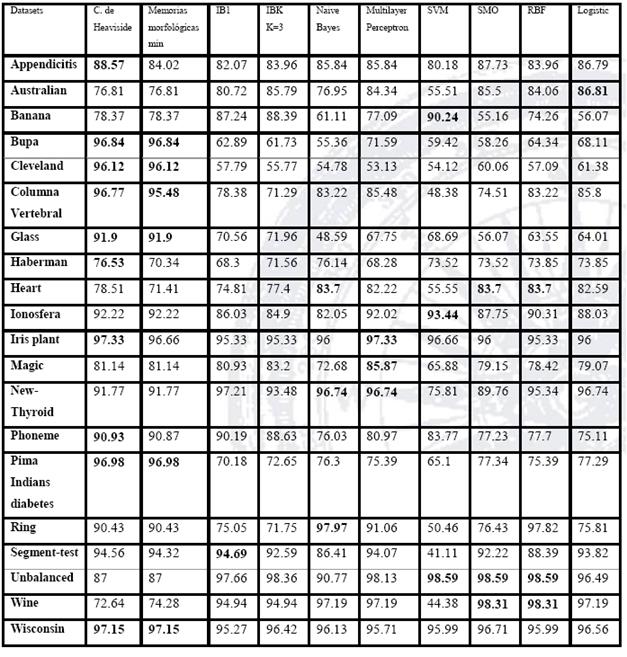
El clasificador de Heaviside fue implementado en Matlab, mientras que las Memorias Morfológicas Min fueron implementadas en Java y para el resto de los modelos se empleó la herramienta Weka (Hall et al., 2009, p. 10). En la Tabla 3 se presenta el desempeño promedio de los algoritmos (calculado con el método de validación K Fold Cross Validation con K=10), en los veinte conjuntos de datos.
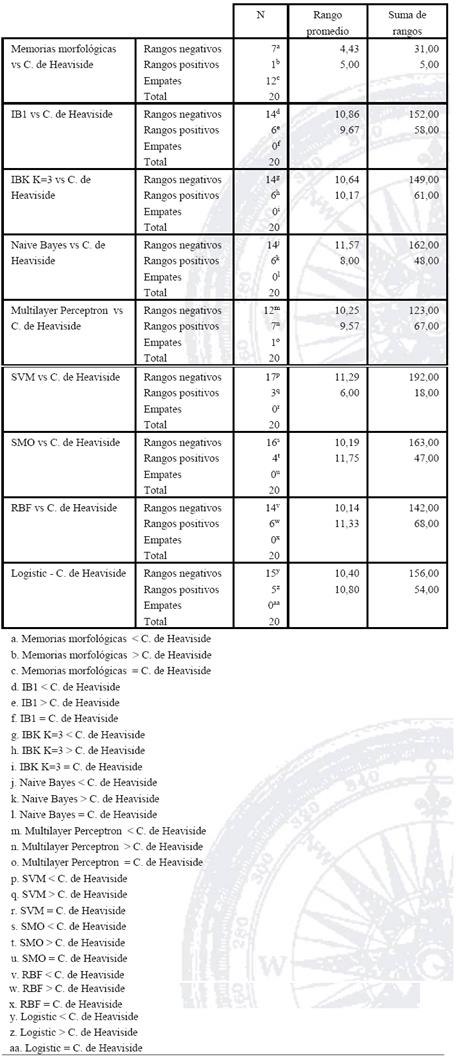
A partir de estos valores se realizó el test de Wilcoxon. Los resultados de la prueba de rangos con signo de Wilcoxon se presentan en la Tabla 4; mientras que en la Tabla 5 se presentan los valores estadísticos de contraste obtenidos de la prueba de Wilcoxon.
De acuerdo con los valores presentados en las Tablas 3, 4 y 5 , es posible afirmar que el Clasificador de Heaviside supera a las Memorias Morfológicas Min, al clasificador 1NN, al clasificador Naive Bayes, a las SVM, al clasificador SMO y a la función logística con un 90% de confianza. Cabe destacar que con un 95% de confianza el clasificador de Heaviside supera al Naive Bayes, a las SVM y al modelo SMO.
Discusión y conclusiones
En este trabajo se ha presentado un nuevo modelo de clasificación supervisada de patrones, el cual está basado en la función de Heaviside; es muy importante mencionar que tras una extensa investigación, en el estado del arte no se encontraron modelos inteligentes de clasificación de aptrones cuya base teórica esté dada por la función de Heaviside.
El modelo de clasificador propuesto destaca por el hecho de que trabaja con patrones enteros no negativos, los cuales pueden ser obtenidos a partir de patrones con valores reales mediante un proceso de transformación. Por ello, es posible representar las componentes de los patrones en cualquier sistema numérico con base mayor que 1.
De igual forma el modelo propuesto en este trabajo, presenta dos operaciones originales, las cuales están basadas en la función de Heaviside: la operación L de aprendizaje, y la operación C de clasificación de patrones. En este artículo se presentaron los fundamentos matemáticos de ambas operaciones y algunas de sus propiedades más importantes.
Después de probar el Clasificador de Heaviside en varios bancos de datos y de comparar sus resultados con los obtenidos por algunos de los modelos más importantes de clasificación de patrones, se destaca el hecho de que el Clasificador de Heaviside es bastante competitivo. También es importante resaltar que se sustentó la validez de los experimentos realizados mediante una prueba no paramétrica.
Además, se está trabajando en ajustes al algoritmo que podrían incrementar de manera importante su rendimiento y performance. Esto posibilitaría su aplicación en problemas de clasificación de patrones donde se requiere un elevado rendimiento y una gran eficacia. Se podría mejorar la eficiencia a través de la implementación del algoritmo en FPGA.
