Introduction
Our objective in this article is to analyze how the emotion of fairness between the members of different groups can affect the outcome of apparently independent games. We extend Matthew Rabin’s (1993) model of fairness, in which individuals want to reciprocate the kindness or unkindness of other individuals, to a more complete model that includes the treatment of other members of our own groups.
In his seminal paper, Rabin introduced the emotion of fairness to game theory. Rabin develops a utility function that incorporates the assumption that players want to be “kind” to other players who are kind with them, and the assumption that players want to be “unkind” to other players that are unkind with them. Rabin develops a solution concept: “fairness equilibria” that includes the emotion of fairness. For example, in the Prisoner´s Dilemma the outcome where both players play “cooperate” may be a fairness equilibrium for small payoffs.
However, some aspects of reality are absent from his analysis. First, individuals see themselves as parts of groups and care about the treatment toward the members of their groups. And second, it is easier for individuals to cooperate if they belong to the same group, for example if they are relatives. There is evidence that individuals tend to treat better those individuals that belong to their own group, even if the group was formed randomly (Chen & Li, 2009; Sherif, Harvey, White, Hood, & Sherif, 1988; Tajfel, Billig, Bundy, & Flament, 1971).
Our objective is to extend Rabin’s Fairness Equilibria to represent fairness between groups. Falk and Fischbacher (2006), Levine (1998), Fehr and Schmidt (1999), and Bolton and Ockenfels (2000) have developed simpler models of reciprocity that do not rely on intentions. However, we focus our analysis in Rabin’s model, because it is the best known model of reciprocity and we believe intentions are essential to represent the emotion of fairness between groups.
In this article we model games where individuals play directly only in pairs. However, we assume that individuals take into consideration the interaction of players in other games when they form their beliefs regarding kindness. While most game theorists have assumed that players only care about what happens in the games they play, our aim is to model how the outcome in one game may affect the outcome of other games.
The closest work to ours is Moreno-Okuno and Mosiño (2017) who model group reciprocity using the framework of Dufwenberg and Kirchsteiger (2004). Although their model is more general than ours (as it applies to games with players and strategies and is defined for dynamic games) our model has the advantage of being closer to the best known model of Rabin. Another advantage is that our model is easier to analyze and the applications are easier to interpret.
In section “Model”, we introduce our model by extending Rabin’s Fairness Equilibria to groups of individuals. Rabin’s model is defined over a single game of two players. However, in order to analyze the interaction between groups of individuals, we have to work with more individuals. We work with the easiest case: Two games of two players in each game, where one of the players in each game belongs to one of two groups.
Rabin defines a belief-of-kindness function that represents how kind an individual A thinks another individual B has acted towards her. We extend this function to include not only A’s beliefs of the kindness or cruelty of B’s actions towards A herself, but also A’s beliefs regarding the kindness or unkindness of other members of B’s group toward other members of A’s group. Next, we define a function of how kind A thinks she has acted towards B. Finally we define a utility function that uses these two kindness functions to represent that an individual wants to be kind to an individual that belongs to a group whose members have been kind to members of her own group and wants to be unkind to an individual that belongs to a group whose members have been unkind to the members of her own group. Our equilibrium occurs when each individual plays in such a way as to maximize his or her own utility and when individuals beliefs regarding other individuals actions are correct and individuals beliefs regarding other individuals beliefs are also correct. We refer to this solution concept as a “group-fairness equilibrium.”
Also, we analyze how the outcome of a single game can impact the outcome of the other game. We get the following results:
First, a combination of strict Nash equilibrium in both games will always be a groupfairness equilibrium for large values of the payoffs. Second, for very high payoffs, there are not positive group-fairness equilibria.
Third, in the case where the payoffs of the games are small, the outcomes where individuals are maximizing the other players’ payoffs is a group-fairness equilibrium if any player do not have a specific grudge for her opponent; and the outcomes where individuals are minimizing the other players payoffs is a group-fairness equilibrium if every player have a positive grudge for their opponents.
In section “Group-Fairness over two periods” we extend our model to the case of two periods, when a single game is played first and then the other. We apply our model to the case of a monopoly that gives away a product for free to an individual in need in order to improve its perception among its consumers. If the individual in need belongs to the same group as the consumer, the consumer may be willing to pay a higher price to the monopoly in order to repay its kindness. The kinder the monopoly is to the individual in need and the closer that individual is to the consumer, the higher the price the consumer will be willing to pay for the product.
In section “Facing somebody from our own group”, we analyze the case where one individual plays against another member of her own group. We assume that individuals think better of members of their own groups and treat them better as a result. In this section we analyze an example in which one consumer buys a product from a monopoly and we show that the consumer is willing to pay a higher price if the owner of the firm belongs to the same group as her.
In section fifth we conclude and discuss possible extensions.
Model
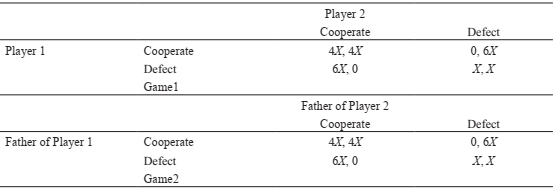
For simplicity, we analyze the case of two games with two players each game, where one player in each game belongs to one of two groups. , N1 = {1,2} is the set of players of the first game, and , N2 = {3,4}, is the set of players of the second game. N = {1,2,3,4}, is the set of players of the whole game that includes game 1 and game 2. We will refer to each game of two players as a “single” game and to both games as the “whole” game.
We assume that there is a partition P of N.P represents the different groups that a player can belong. With this partition, we are assuming that every player belongs to a group, and only one group of P. For example, can be the partition of two groups: odd players and even players.
Si is the set of (possible mixed) strategies for
player i ϵ N,αi
ϵ Si is a strategy for individual
i, bij
ϵ Si are the beliefs of individual
i regarding the strategy of individual j, and
ciji
ϵ Sj are the beliefs of individual
i about the beliefs of the individual j
concerning her own strategies (second order beliefs). These last two variables refer
to the beliefs that individuals have as regards the strategies and beliefs of their
opponents. Because we analyze games of two players each game, the payoffs for player
i are given by
Individuals sometimes belong to groups whose members are very tightly-knit, such as members of the same family, and sometimes belong to groups whose members are not so tightly-knit. We use the variable v ϵ [0,1] to represent the closeness of the members of the groups that play in both games. We include this term to represent the idea that as the affiliation between the players grows strong so grows the extent to which other individuals relate their actions and intentions. A player would care more about the outcome of another game if somebody she is related to plays in that game. Similarly, a player would form stronger emotions towards her opponent if her opponent is related to somebody that plays in the other game. If v = 1 players care as much about the other member of their group as they do about themselves and if v = 0, players are not related and do not care about the treatment of the players in the other game.
We introduce the variable
We define a kindness function, which is taken from Rabin (1993), representing how kind an individual believes she is to her opponent.
Definition 1: The kindness of player i towards player j is given by:
where
Definition 2: The beliefs about kindness of player i, that belongs to group Q ϵ P, about the kindness of player j (and j’s partner) is given by:
where i, k ϵ Q and
The first two terms of the numerator and the denominator of
The choice of
Now we define a player’s utility function using our definitions of kindness functions.
Definition 3: The utility of individual is given by:
This utility function represents a situation where an individual’s utility increases if she is kind to somebody that is kind to her (or if she is kind to the partner of somebody that is kind to her own partner) and unkind to somebody that is unkind (or if she is unkind to the partner of somebody that is unkind to her own partner). We now define a new solution concept that includes the idea that an individual wants to reciprocate when playing against somebody that belongs to a group in which somebody has been kind or unkind to somebody in her own group. We name this solution concept: “Croup-Fairness equilibria”. We follow Ceanakoplos, Pearce, & Stacchetti (1989), and Rabin (1993), to require that in equilibrium, every player’s beliefs have to match both their beliefs regarding beliefs and their strategies.
Definition 4: The strategy profile a* ϵ A is a Croup-Fairness Equilibrium if for all i,j,k,l ϵ N we have:
This solution concept represents the emotion of fairness where in the presence of acts of kindness or unkindness, individuals may want to reciprocate not only to those individuals who committed the acts, but also to every member of the same group, even those that does not have any relation to those acts. As a result, the outcomes of different games for members of the same groups may be related.
One drawback of using Rabin’s “fairness equilibrium” as a framework for our model is that we cannot prove the existence of the group-fairness equilibrium defined above, as the utility function is not continuous. However, we work with Rabin’s framework given its clarity and the familiarity of his model.
Basic results
In this section we analyze the relation that exists between the outcome of two games. We pay special attention to analyze the cases where a particular liking or grudge can affect the outcome of both games. We give some general propositions, but before, we write three of Rabin’s definitions that we use in our results. Rabin works with a game of two players and therefore his definitions are for a game of two players. The first two definitions: a mutual- min and mutual-max strategies are useful as they are, but we extend the third one, the definition of positive and negative outcomes, for the case of two games of two players each game.
Rabin defines a mutual-max strategy as a strategy where both players mutually maximize each other’s material payoffs and a mutual-min strategy as a strategy where both players mutually minimize each other’s material payoffs. An example of a mutual-max strategy is where both players, in the battle of the sexes, go to the same event, and an example of a mutual-min is where both players, in the prisoner´s dilemma, play defect.
Definition 5: A strategy pair (ai,
aj) ϵ
(Si,
Sj) is a mutual-max outcome
f or a single game g if, for
Definition 6: A strategy pair (ai,
aj) ϵ
(Si,
Sj) is a mutual-min outcome
f or a single game g if, for
Other definition that we take from Rabin, is that of a positive and negative outcome. Rabin defines the outcome of a game as a positive if the sign of the kindness function for both players is positive and negative if the sign of the kindness function for both players is negative. We extend Rabin’s definition of positive and negative outcomes for the case of two games and four players by defining a positive outcome as an outcome where the four players are kind and a negative outcome for the case of two games as an outcome where the four players are unkind.
Definition 7: a) An outcome is strictly positive for the two games case if for i ϵ N,fi > 0 b) An outcome is weakly positive if for i ϵ N,fi ≥ 0. c) An outcome is strictly negative if for ,. i ϵ N,fi < 0 d) An outcome is weakly negative if for i ϵ N,fi ≤ 0.
Now we use these definitions in the following propositions. In proposition 1 we show the relation that exists between group-fairness equilibria and the Nash equilibria of both games when the material payoffs are high. For this, we analyze a set of games that are exactly the same, except that the size of their material payoffs vary with a variable X.
Given that the material payoffs for each player only depend on the strategies of herself and her opposite, we can think of the whole game as composed of two materially independent games, one formed by players 1 and 2 and the other formed by players 3 and 4. Let g1 be the set of games that consists of players 1 and 2 and the set of strategies S1 and S1 and payoff functions , X∙π1 (a1, a2) and , X∙π2 (a1, a2). Let G1 (X) ϵ g1 be the game that corresponds to X. Let g2 be the set of games that consists of players 3 and 4, the set of strategies S3 and S4 and payoff functions , X∙π3 (a3, a4) and X∙π4 (a3, a4). Let G2 (X) ϵ g2 be the game that corresponds to X.
Let’s denote the whole game that is composed by games G1(X) and G2 (X) as , G(X,X). We sometimes refer to , G(X,X) as “the composite game” and to G1(X) as “single game 1” and to G2 (X) as “single game 2”.
Proposition 1: a) If an outcome a is a combination of strict Nash equilibrium in games 1 and 2, there is a
Proposition 1 is a direct translation of Rabin’s propo.sition 5 to group- fairness. (The proof of proposition 1, as well as all other proofs are in the Appendix.) If the material payoffs increase, the importance of fairness considerations becomes smaller. As the material payoffs increase arbitrarily, eventually the material payoffs dominate the fairness considerations and the group-fairness equilibria become the combination of Nash equilibria for both games. Proposition 2 tell us that as the material payoffs grow arbitrarily large in both games, players cannot have positive emotions.
Proposition 2: There is a
Proposition 2 tell us that as the material payoffs grow large, the positive group-fairness equilibria are eliminated and only the weakly negative and neutral group-fairness equilibria are left. As the income increases, the material payoffs dominate the fairness considerations. Because individuals are maximizing their own material payoffs, other players would not think they are being kind and the positive emotions are eliminated. Proposition 3 analyzes group-fairness when the material payoffs for both games become small. Part a) of the proposition tell us that any combination of mutual- max and any combination of mutual-min is a group-fairness equilibrium is a group-fairness equilibrium when the material payoffs are very small and individuals have an exogenous liking (grudge) for their opponents. Part b) tells us that when every game has only one mutual-max (mutual-min) outcome and the material payoffs are very small and individuals have an exogenous liking (grudge) for their opponents, then the combination of these outcomes are a group-fairness equilibrium.
Proposition 3: For any outcome a that is strictly mutual-max (mutual- min) for both games, there exists an
Part a) of proposition 3 is a direct translation of Rabin’s proposition 3. As material payoffs approach zero, the game is dominated by the fairness considerations. In the case that an outcome that is strictly mutual-max for both games, every player is playing a strategy that maximizes the material payoffs of the other player and therefore they are being kind to each other (or at least, they are not unkind to each other). If no player has a grudge against each other, nobody wants to change their strategy since they want to be kind to each other in response. In the case that an outcome is a strictly mutual-min for both games, every player is playing a strategy that minimizes the material payoffs of the other player and therefore they are being unkind to each other. In this case, if no player has a special liking for the player they are playing with, nobody wants to change strategy since they want to be unkind to each other in response. Part b) tell us the effect that exogenous grudges or likings of the individuals can have in the outcome of the game. In the case that each game has one mutual-max outcome and the material payoffs are small, then if every player has a liking for her opposite player, the group-fairness of the game has to be the combination of the mutual-max for each game. In the case that each game has one mutual-min outcome and the material payoffs are small, then if every player has a grudge against her opposite player, then the group-fairness of the game has to be the combination of the mutual-min for each game.
The last three propositions refer to the case where the material payoffs increase or decrease for both games. In the next two propositions we analyze the group-fairness when the material payoffs of one game change while the material payoffs for the other game are left constant. We define the playoffs of game one as function of X and the payoffs of game two as a function of Y as in Figure 2. Now, g2 represents the set of games that consists of players 3 and 4 and payoff functions Y∙π3(a3,a4) and Y∙π4(a3,a4). G2 (Y) ϵ g2 is the game that corresponds to Y. We denote the whole game that is composed by games G1 (X) and G2 (Y) as G(X,Y).
We analyze the case where Y changes, but X is kept constant. We assume in these propositions that v is positive, since if it were zero, it would be equivalent to two single independent games.
Proposition 4 refers to the case where the material payoffs of one game grow large. As the material payoffs of one game grow, the fairness consideration of this game dominate the fairness consideration of the other game. If the outcome of this game is strictly negative, then both players in this game are unkind to each other and (if nobody has an exogenous liking) both players in the other game do not want to be kind to each other (they will not necessarily will be unkind, as this depends also of the material payoffs, however, they will not be kind).
Proposition 4: There is a
Proposition 5 refers to the case where the material payoffs of one game become very small, while the material payoffs for the other game are left constant. As the material payoffs of one game become small, individuals care more about what’s happen in the other game and the emotions of fairness for that game would be dominated by the emotions of fairness of the other game: players would be kind if the players in the other game are kind and players would be unkind if players in the other game are unkind. In this scenario, a player in game 1 with a large enough liking or grudge to determine the outcome of the single game, will also determine the outcome for game 2 and the groupfairness equilibria for the whole game.
Proposition 5: There is a
In Figure 2, as Y becomes small, players in game 2 cooperate only if players in game 1 also cooperate and they defect if players in game 1 defect. In the case that a player in game 1 has a grudge or liking against the other individual, then she will have an impact in not only in game 1, but also in game 2.
Group-Fairness over two periods
In this section, we extend our model to include the secuential case, where one game is played first and then the other, in order include the situation where players anticipate that the kindness or unkindness of their actions will have an effect on the behavior of other players. For example, firms may donate to charity in order to influence consumers, who may want to buy from kind firms. Similarly, some individuals may commit hate crimes to generate negative emotions among the members of opposing ethnic groups in order to create divisions. In this section, we extend our model of group-fairness to the two period case where single game 1 is played first and then single game 2. Players in single game 1 may want to influence the actions of players in game 2.
Dufwenberg and Kirchsteiger (2004), analyze sequential games where the beliefs are revised as the game progresses. Our model, however, is much more simple that the ones they analyze. Other than assuming that single game 1 is played first and single game 2 is played second, we assume that there are no differences with respect to the case where both games are played simultaneously and that the individuals beliefs regarding kindness are the same. In doing so, we are implicitly assuming that individuals in the second period are myopic and do not take into consideration the fact that individuals in the first period may be kind or unkind in order to influence their decisions in the second period. This assumption allows us to find the group-fairness equilibrium of the complete game by backward induction and allows us to analyze how individuals try to influence the emotions of other individuals. We believe this situation represents many cases that exist in reality and that individuals are at least partially myopic as to the intentions of other players.
Definition 8: The strategy profile a* is a Group-Fairness Equilibrium over two periods if for i,j = 1,2, and i ≠ j, and
for all m,n ϵ N.
Note that for players 3 and 4,
Players in game 1 maximize their utility in the knowledge that their actions will affect the actions of players in game 2. Given that they want their partners to be treated kindly in game 2, they may be kind in the first period in order to make their partner’s opponent be kind in return, even if they are treated badly. Huck and Lünser (2010) show that in trust games individuals help their partners in order to improve the reputation of their group.1 Abbink and Herrmann (2009) create a game where members of two groups can repay offences against their own groups that results in a “Vendetta”.
Application: Firms giving to charity
Rabin (1993) shows that when individuals care about fairness, a monopoly cannot extract the entire consumer surplus given that individuals see this as an unfair practice and retaliate by not buying its product. However, consumers care not only about how the monopoly treats them, but how it treats other individuals, especially how it treats other members of their own groups. In this section we extend Rabin’s example to show that a consumer is willing to pay a higher price for a product from a monopoly that has helped a member of their own group. According to Creyer (1997) consumers are willing to reward a company ethical behavior by paying a higher price for its products.
We assume that there is a single consumer who wants to buy a single unit of a product from a monopoly. The consumer’s valuation of the product is given by β, while the marginal cost for the monopoly is zero. Simultaneously, the monopoly chooses the price and the consumer chooses a reservation price r, above which she is not willing to pay. We assume that the monopoly can improve how kind the consumer thinks of it by being kind to another player: an individual in need that belongs to the same group as the consumer. Let us consider the case of an individual in need who values the help of the monopoly at Φ but cannot repay that help in any way. With respect to this individual, the monopoly has only two options: to help her or not. If the monopoly helps, it will incur a cost of c, yet the consumer will think better of it, whereas if the monopoly does not help the individual in need, the consumer will think worse of it.
The timing of the game is as follows: in the first period the monopoly decides whether or not to help the individual in need and in the second period the monopoly sells its product to the consumer. We solve this problem by backward induction. In the second period, the consumer chooses the reservation price (r) and the monopoly simultaneously chooses the price. We assume that the consumer has no exogenous liking or disliking for the monopoly (in the next section we analyze the case in which the consumer has a liking for the monopoly derived from the consumer’s belonging to the same group as the owner of the monopoly). If p ≥ r, the consumer buys the product.
If the monopoly helps the individual in need in the first period and if the monopoly prices at p = r = z (i.e., it charges the highest price that the consumer is willing to pay) in the second period, the consumer believes the kindness of the monopoly to be as follows:
where v is the degree of closeness between the consumer and the individual in need. If the monopoly doesn’t help the individual in need in the first period, the consumer believes the kindness of the monopoly to be as follows:
If the consumer buys the product from the monopoly, she will not be being kind to the monopoly, given that she is performing an action that improves her own material payoffs (unless the consumer pays a higher price that her valuation of the product). However, if she does not buy the product (by choosing a reservation price higher than the price of the monopoly) she will be unkind, given that she is sacrificing her material payoffs in order to punish the monopoly.
In the second period, the monopoly charges a price that makes the consumer indifferent between consuming and not consuming. The maximum price the monopoly is able to charge is:
and if the monopoly doesn’t help the individual in need, the maximum price that the monopoly is able to charge is:
therefore, the monopoly is able to increase its price by helping the individual in need. If the cost of helping the individual in need is lower than the extra revenue this brings, that is, if
We should note that the price the consumer is willing to pay can be higher than her valuation of the product. If v ϕ>1, equation (1) is higher than the valuation of the product, and therefore the consumer thinks that the monopoly is kind, not only to the individual in need but kind overall, and the consumer is willing to pay a higher price than her valuation in order to be kind in response to the monopoly. For example, many people buy cookies that are sold by girl scouts at a higher price than their actual valuation of the cookies because they want to help the organization as much as they want to eat the cookies.
Facing somebody from our own group
As mentioned in the introduction, individuals tend to treat those individuals that belong to their own groups better. In Prisoners Dilemma experiments, cooperation is more common between members of the same group (Yamag-ishi & Kiyonari, 2000). Chen and Li (2009) also show that individuals are more likely to reward a member of their own group for good behavior and less likely to punish when misbehavior. We can represent this observation by assuming that when an individual face a member of her own group, her exogenous liking for her opponent is an increasing function of how tightly-knit the members of the group are. For example, we can assume the simple form σij (v) ≡ v. In this section we analyze the case of a single game where both players are members of the same group.
Rabin (1993) shows that in the Prisoner´s Dilemma the cooperative outcome exists for low values of X. For a single game with two players and σij (v) ≡ v, the belief-of-kindness from equation 1 reduces to:
this is equivalent to the kindness function of Rabin (1993) except for the addition of v.
By including ν, our model takes into account that if both players belong to the same group, cooperation may be sustained for higher values of X. The group-fairness equilibrium where both players cooperate exists if X ≤ 1/4 + v that is, for members of more tightly-knit groups the outcome where both individuals cooperate exists for higher values of the material payoffs. Additionally, if v > 1/2 , the equilibrium where both players play “defect” does not exist for low values of X (for values of X smaller than v, that is, individuals that belong to tight-knit groups always cooperate for small material payoffs.
As family members are less likely to defect in a Prisoner´s Dilemma-type situation, then in some cases institutions will be organized around members of the same family. For example, Bloom and Van Reenen (2010) argue that in many developing countries, family businesses may be reluctant to hire managers from outside their families because the weak rule of law there does not protect them from theft from outside individuals.
Application: Consumers buy from a company from within their own group
There is evidence that individuals in developed countries evaluate the products from their own countries more favorably (Bilkey & Ness, 1982). If an individual does so, she will be willing to pay a higher price for a product from her own country than one from another country.
We extend the example in the section “Application: Firms giving to Charity” by assuming that
the consumer has an exogenous liking for the monopoly that is a lineal function of
the closeness of the owner of the monopoly to the consumer:
σij (v) ≡
v. We exclude from the analysis the individual in need and
assume that there are only two players: a monopoly and a consumer. The consumer
considers that the kindness of the monopoly towards her when the monopoly chooses
p = z is
An individual is willing to pay a higher price the higher the value of v, that is, the higher the closeness of the group to which the owner of the company and the consumer belong.
In equation (2) we can see that for v > 1/2, the consumer is willing to pay a price higher than her valuation of the product.
Conclusions
In this article we extended Matthew Rabin’s (1993) model of fairness equilibrium to groups of individuals. First, we introduced a utility function that represents that individuals not only have emotions of fairness toward other individuals with which they interact, but with those that belong to groups whose members have been kind or unkind toward members of their own groups. We model the interaction of four players playing in two games (two games with two players each game.) We assume that there are two groups, with two members in each group. We assume that one member of each group plays in each game.
Second, we used our utility function to define a new solution concept: “groupfairness equilibrium” and analyzed the relation between the outcome of both games. Finally, we applied our model to explain why firms invest in programs of social responsibility to improve their image, which increases the price that customers are willing to pay for their products.
Our work could be extended in a number of ways. For example, group-fairness could be paired with generalized reciprocity. Generalized reciprocity is when an individual (that is not related at all) is targeted by the offences of third parties. This could explain why minorities sometimes are targeted on hard times, even if the minorities does not have anything to do with the problems.











 text new page (beta)
text new page (beta)