Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
EconoQuantum
On-line version ISSN 2007-9869Print version ISSN 1870-6622
EconoQuantum vol.10 n.2 Zapopan Jul./Dec. 2013
Suplemento
Generalized impulse response analysis: General or Extreme?1
Hyeongwoo Kim2
2 Department of Economics, Auburn University, Auburn, AL 36849. Tel: 334-844-2928. Fax: 334-844-4615. Email: gmmkim@gmail.com.
Recepción: 01/11/2012
Aceptación: 25/06/2013
Abstract
This note discusses a pitfall of using the generalized impulse response function (GIRF) in vector autoregressive (VAR) models (Pesaran and Shin, 1998). The GIRF is general because it is invariant to the ordering of the variables in the VAR. The GIRF, in fact, is extreme because it yields a set of response functions that are based on extreme identifying assumptions that contradict each other, unless the covariance matrix is diagonal. With a help of empirical examples, the present note demonstrates that the GIRF may yield quite misleading economic inferences.
Keywords: Generalized Impulse Response Function; Orthogonalized Impulse Response Function; Vector Autoregressive Models.
JEL Classification: C13; C32; C51.
Resumen
Esta nota analiza la limitación de utilizar la función generalizada de impulso-respuesta (FGIR) de los modelos autoregresivos VAR (Pesaran y Shin, 1998). El FGIR es invariante al orden del rezago de las variables asociadas al modelo VAR . De hecho, el FGIR produce un conjunto de funciones respuestas con base a supuestos de identificación extremos que se contradicen entre ellos, a menos que la matriz de covarianza sea diagonal. Con la ayuda de ejemplos empíricos, la presente nota demuestra que el FGIR puede generar inferencias incorrectas.
Introduction
Notwithstanding its popularity, the orthogonalized impulse response function (OIRF; Sims, 1980) analysis of structural vector autoregressive (VAR) models is subject to the so-called World-ordering problem.3 That is, when one changes the order of the VAR with an alternative identifying assumption, she it may obtain dramatically di erent response functions (Lütkepohl, 1991).
Pesaran and Shin (1998) propose the generalized impulse response function (GIRF), an ordering-invariant approach, based on the work of Koop et al. (1996). The GIRF has been employed by many researchers: Boyd et al. (2001), Cheung et al. (2004), and Huang et al. (2008), to name a few. This note shows, however, that the GIRF may result in misleading inferences caused by its extreme identification schemes.
The remainder of this note is organized as follows. Section A Pitfall of the GIRF analytically demonstrates why the GIRF actually can be considered extreme in perspective of its identification method. In Section Empirical Examples, I provide two empirical examples that highlight substantial different between the GIRF and the OIRF and the last Section conclusions.
A Pitfall of the GIRF
This section provides a simple analytical explanation on a pitfall in using the GIRF, which demonstrates potentially serious problems of using the GIRF.
Let Ψyjg (n) and Ψyj0(n) denote the GIRF and the OIRF at time t + n respectively, when there is one standard error shock at time t to the jth variable in an m-variate VAR with yt = [y1,t y2,t ... ym,t]'. Pesaran and Shin's (1998) Proposition 3.1 implies Ψy1g (n) and Ψy10(n).4 Define  as the OIRF when yj,t, is ordered first in yt. By construction,
as the OIRF when yj,t, is ordered first in yt. By construction, Now re-order the vector so that yt = [y2,t , y1,t , y3,t ,... ym,t]', which yields
Now re-order the vector so that yt = [y2,t , y1,t , y3,t ,... ym,t]', which yields  by the proposition and because the GIRF is invariant to the ordering of the variables in yt. Repeat this procedure until we get
by the proposition and because the GIRF is invariant to the ordering of the variables in yt. Repeat this procedure until we get 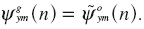 Collecting these response functions, the GIRF for the entire system is,
Collecting these response functions, the GIRF for the entire system is,
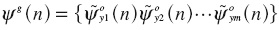
The GIRF, therefore, is not general in effect because it employs extreme identifying assumptions that each variable is ordered first. More seriously,  and
and  are not consistent with each other when i ≠ j unless the covariance matrix is diagonal. For instance,
are not consistent with each other when i ≠ j unless the covariance matrix is diagonal. For instance,  assumes that yi,t is not contemporaneously affected by all other variables including yj,t, while
assumes that yi,t is not contemporaneously affected by all other variables including yj,t, while  needs an assumption that yu is not contemporaneously affected by all other variables including yi,t .5 Hence, the GIRFs conflict each other. This result also trivially applies to vector error correction models.
needs an assumption that yu is not contemporaneously affected by all other variables including yi,t .5 Hence, the GIRFs conflict each other. This result also trivially applies to vector error correction models.
In the next section, I show that such inconsistency may lead to misleading economic inferences.
Empirical Examples
This section provides empirical illustration to compare the implications of the GIRF with those of the OIRF.
I first use a quadvariate VAR model of the US per capita investment (i), consumption (c) , real GDP (y), and the government expenditure share (g) relative to the real GDP, measured in logarithms. The data frequency is quarterly and the observations span from 1948Q1 to 2008Q4, obtained from the Federal Reserve Bank of St. Louis FRED data base.
I report the ordering-free GIRF and the OIRF with an ordering [i c g y] to a government expenditure shock in Figure 1.6 Both response functions display a decrease in i, which may be consistent with the crowding-out effect. However, responses of c and y exhibit noticeably different dynamic adjustments. For example, the GIRF implies a significant decrease in y at the 5% level over a year, while the OIRF implies significantly positive responses of y for about a year. Since y includes not only private but also public sector outputs, it is surprising to see a substantial decrease in y in the short-run as we have seen from the GIRF.7 Similarly, the GIRF implies a significant decrease in c for about a year, while the OIRF displays slow positive adjustments of c which are insigniicant.
I implement another example to better understand why there may be such differences between the GIRF and the OIRF. For this, I use a trivariate VAR model of i, c, and y from the previous exercise, which was also employed by Pesaran and Shin (1998).
Note that the GIRFs to (one standard error) investment shock (Panel 2-a in Figure 2) coincide with the OIRFs to an i-shock when i is assumed to be contemporaneously unaffected by other two variables, c and y (Panel 2-b). Note also that under this assumption, the OIRFs to a y-shock are very different from the corresponding GIRFs. However, the GIRFs to a y-shock are identical to the OIRFs when y is ordered irst in the VAR (Panel 2-d) by construction. Again, the other OIRFs under that assumption are quite different from the corresponding GIRFs. Likewise, the GIRFs to a c-shock are identical only to the OIRFs to a c-shock when c is ordered irst (Panel 2-c).
Based on these indings, it seems important to estimate and report response functions based on the underlying economic model. For example, if one interprets y-shocks as an output (supply) shock, while i-shocks and c-shocks are treated as expenditure (demand) shocks, she may employ an ordering [yic] assuming that y does not contemporaneously respond to demand shocks. Then, she will report the response functions to an i-shock, for instance, that are very different from the GIRFs both quantitatively and qualitatively. If one believes that i is primarily driven by animal spirit, she may employ [i y c] instead and report quite smaller responses of i to a y-shock than the corresponding GIRF.
Conclusion
This note points out that there is a pitfall in using the GIRF. Economic inferences based on the GIRF can be misleading because the GIRF employs a set of extreme identifying assumptions that contradict each other unless the covariance matrix is diagonal. Our empirical example demonstrates that this is by no means a negligible matter. In such cases, it would be more reasonable to use identifying assumptions that consistently describe the underlying economic model.
References
Boyd, D., Caporale, G.M., & Smith, R. (2001). "Real Exchange Rate Effects on the Balance of Trade: Cointegration and the Marshall-Lerner Condition". International Journal of Finance and Economics, 6: 187-200. [ Links ]
Cheung, Y., Lai, K., & Bergman, M. (2004). "Dissecting the PPP Puzzle: The Unconventional Roles of Nominal Exchange Rate and Price Adjustments". Journal of International Economics, 64: 135-150. [ Links ]
Huang, Y., Neftci, S.N., & Guo, F. (2008). "Swap Curve Dynamics Across Markets: Case of US Dollar versus HK Dollar". Journal of International Financial Markets, Institutions and Money, 18: 79-93. [ Links ]
Koop, G., Pesaran, M.H. & Potter, S. (1996). Impulse Response Analysis in Nonlinear Multivariate Models. Journal of Econometrics, 74: 119-147. [ Links ]
Lütkephol, H. (1991). Introduction to Multiple Time Series Analysis. Germany: Springer-Verlag, Berlin. [ Links ]
Pesaran, M. H. & Shin, Y. (1998). Generalized Impulse Response Analysis in Linear Multivariate Models. Economics Letters, 58: 17-29. [ Links ]
Sims, C. (1980). Macroeconomics and Reality. Econometrica, 48: 1-48. [ Links ]
1 A thank goes to Michael Stern for helpful comments. Madeline Kim provided excellent research assistance.
3 The OIRF recursively identifies the structural shocks by using the Choleski decomposition factor of the covariance matrix, which yields a unique lower triangular matrix. This scheme, therefore, assumes that the variable ordered first in the VAR is contemporaneously unaffected by all other variables.
4 That is, GIRF and the OIRF coincide for the shock to the first variable in yt.
5 If it is diagonal, there is no gain of using a structural VAR model, because it coincides with a reducted-form VAR, in other words, equation-by-equation least squares estimations.
6 95% conidence bands are obtained from 5,000 nonparametric bootstrap simulations.
7 For this, private sector activities should decrease by more than one increase in the increases in the public sector.














