PACS: 52.27.Gr; 41.20.Cv; 02.30.Hq
1. Introduction
One of the most elementary concepts in classical plasma physics is that of Debye shielding, which establishes the characteristic distance λD in which the electrostatic field from a charged test particle can be shielded by particles of the opposite sign. If a test charge is placed in a homogenous plasma, in which the unperturbed electron and ion densities are the same (i.e.: satisfy the quasi-neutrality condition), it repels the charges of its own sign, while it “dresses” itself with charges of the opposite sign, resulting in an electrostatic shielding. The derivation of λD has been well presented with similar arguments in many textbooks, such as Refs. 1 to 7. In doing so, two assumptions are generally made: (i) The total kinetic energy of the particles is much greater than the electrostatic interaction energy between them, which means that the plasma is weakly coupled, and allows the linearization of the problem, (ii) Each particle species is in thermodynamic equilibrium, so their velocity distributions are Maxwellian. The latter assumption requires the density to be large enough to allow collisions to an equilibrium state, and does not apply for collision-less, non-equilibrium plasmas, such as those often found in space plasmas.
Modern textbooks discuss the case of strongly coupled plasmas, for which the first constraint does not apply 3,5,8, although they usually ignore the fact that many collision-less plasmas, particularly in space physics, even in steady state, are non-equilibrium systems, and therefore not Maxwellian. The case of shielding in quantum plasmas, in which Fermi statistics should be considered, has been presented in Ref. 8, but it will not concern us in this paper.
The question on the relaxation of assumption (ii) has been addressed by Bryant 9, who studied the shielding produced when the species are described by the so called kappadistributions for non-equilibrium plasmas. This is a more general family of distributions that include the MaxwellBoltzmann one as a special case, and is motivated by observations in space plasmas. While Bryant’s conclusion is that the shielding λD is shorter than for the Maxwellian case, given the same number density and mean energy, the weakly coupled assumption is kept. More recently, Livadiotis and Comas have reviewed the subject, providing a better theoretical ground for the kappa-distributions, under the point of view of non-extensive entropy 10. At a didactical level MeyerVernet 11 studied the case in which a Boltzmann equilibrium is not assumed, from a different point of view.
On the other hand, the weakly coupled plasma assumption, also poses the requirement that the number of particles ND within a sphere of radius λD be much greater than 1, so the case of classical strongly coupled plasmas, in which ND ∼ 1 (in the opposite limit of that of quantum plasmas, for which ND ≫ 1) is left open. It is also important to note that the linearized solution for the electrostatic potential, which results from the weakly coupled plasma assumption, is also limited in space, and breaks down for r < λD. The relaxation of the weakly coupled plasma assumption has been addressed by Mak 12, who compared the usual linearized solution for the electrostatic potential with the exact solution of Poisson’s equation for several cases in which ND À 1. While the conclusion was that the approximate solution is good beyond expectation for the cases studied, a few questions went unanswered. Particularly, when does the approximate solution breaks down as ND and the distance r are reduced?
The purpose of this paper is to provide a better insight into the subject, using the same normalised approach as in Ref. 12, for comparison. In Sec. 2 we go through the usual discussion of the problem, reviewing what has been presented in textbooks, for the sake of completeness and in order to establish the notation. In Sec. 3 we compare the approximate analytical solution to the linearized problem with the exact numerical one, and in Sec. 4 we summarise the main conclusions. The paper is written with sufficient detail, for easy reading by an advanced undergraduate or graduate physics student.
2. Linearized Debye shielding
2.1. The Poisson equation
Let us consider a homogeneous plasma, in which the unperturbed large-scale average electron and ion densities neo, and nio, are equal: neo = nio = n. If a point test charge is introduced at the origin, it will create an electrostatic potential Φ(r), which only depends on the radial coordinate r, and which must satisfy Poisson’s equation
where ρc(r) is the charge density distribution. We make the usual assumptions (i) and (ii) mentioned in the introduction, and following Ref. 12, we make an additional assumption: (iii) The positive ions are protons with infinite inertia, so they form a uniform background of density n. Since the electron density would then be given by ne(r) = nexp(eΦ(r)/kT), where −e is the charge of the electron, k is Boltzmann’s constant, and T is the electron temperature, then ρc (r) = ne[1−exp(eΦ(r)/kT)], and Eq (1) can be rewritten as
The numerical solution to this equation is what we shall call the “exact solution”.
2.2. The limit between weakly and strongly coupled plasmas
In this subsection we follow the discussion of Refs. 6 and 7, with some adaptations. The boundary between weakly and strongly coupled plasmas can be established when the electrostatic energy between the plasma particles is equal to the kinetic energy between them, so weakly coupled plasmas are those for which the former is smaller than the latter, and the strongly coupled plasmas are represented by the opposite case. If we consider an electron with velocity v and charge −e in the presence of an ion with charge Ze at rest, the distance of maximum approach rc will be defined by
Taking v as the thermal velocity vth, in the case of three dimensions for an isotropic plasma, we can write
which can be taken as the limiting case in Poisson’s equation, such that weakly coupled plasmas happen for the right hand side is smaller than 3/2, and the opposite case for strongly coupled plasmas. For a weakly coupled plasma,
in which we may take 1 instead of 3/2. Let us now define the Debye length
from which it becomes clear that weakly coupled plasmas are those for which both rd and λD are greater than the maximum approach distance rc. Using this result, it is easy to find that, if we define Λ = λD/rc, as the ratio between the Debye length (the distance in linearized theory at which the electrostatic potential decays to e−1 in the linear theory studied in the next subsection,) and the distance of maximum approach, we find that in the limit between weakly and strongly coupled plasmas, Λ = (3/Z)ND, where
2.3. The weakly coupled limit
The linearization for the weakly coupled plasmas arises after considering Φ(r)/kT ≪ 1, which states the potential energy between the particles is much smaller than their kinetic energy, and is equivalent to
whose solution is the well known Yukawa potential:
By taking the integration constant A = Ze/(4πεo), this allows the usual interpretation of the potential produced by a point charge of an ion Ze, with atomic number Z, at the origin (ρc(r) = Zeδ(r)), where δ(r) is the Dirac delta function), shielded by the electrons with a characteristic decay length λD. Once the electrostatic potential is known, the charge distribution for the linearized solution can be obtained from Eq. (1)
The subtlety in obtaining (9) is discussed in Appendix. The effect of the shielding can be appreciated by computing the charge within a sphere of radius r:
Thus, the charge is Ze at r = 0, and decays to 0 for large r. At the Debye radius the charge is Q(λD ) = 2exp(−1)Ze ∼ 0.736Ze, and falls to half its value at the origin, 0.5Ze, at r/λD ∼ 1.68, well beyond the Debye radius. This result is interesting, when considering λD as the cut-off impact parameter, when Coulomb collisions are considered.
3. Comparison between an accurate (numerical) and the approximate (analytical) solution
For the sake of comparison with Ref. 12, let us normalise the distance r and the potential Φ(r) in terms of the Debye length, changing to the following dimensionless variables:
Thus, Poisson’s Eq. (2) for the potential can be rewritten as
whose numerical solution we shall call the “exact” solution, while the normalized approximate solution would then be
valid for
The main purpose of this paper is to compare the numerical solution Ψ(ρ) to Eq. (13), with the analytic solution (14) to the linearized equation.
Indeed, the approximation should be good for large distances, but Eq. (13) also tells us that it will break down for short distances (exp(−ρ) ∼ 1) when NDρ ≤ 1. This will happen if ND< 1, in very diluted plasmas, or for short distances, when r < λD. Also, remembering Subsec. 2.1, note that NDρ = 4πnλ2Dr = (Z/3)(r/rc), which means that for Z = 1, NDρ > 1 for r > 3rc. Therefore, the weak plasma approximation is expected to break around
for short distances.
However, in order to fully understand what all this means, it is important to quantify these statements. The main purpose of this paper is to compare the numerical solution Ψ(ρ) to Eq. (13), with the analytic solution Ψa (ρ), (14), to the linearized equation.
The numerical solutions are obtained by means of a fourth-order Runge-Kutta routine 13, which is started at the tail of the solution, and integrated backwards, from larger to smaller distances. The initial values ρ0 for the integration can be chosen to be smaller for larger values of ND, because the validity of the approximation breaks at shorter distances. The way in which they were chosen was such that in the first step of integration we satisfy |Ψa −Ψ| < 10−11. It was found that if this condition was not met, the integration would not be independent of the initial condition, which is something else we sought. This of course, also depends on the step of integration. Another criterion used in order to choose the step of integration was based on the tolerance at which the approximation would break. For this purpose, three different tolerances, τ, were tried: 1, 5, and 10%. By trial and error, the integration steps were chosen in such a way that the distance ρd at which (|Ψa − Ψ|/Ψ) × 100 = τ occurred, would be such that τ could be determined within a 0.1% uncertainty.
A first result of this calculation we found, is that the approximate solution underestimates the exact one. Table I shows, for several values of ND , the initial values ρ0 of the integration, and the values ρd for which tolerances of 1, 5 and 10% between the two solutions fail. The same results are plotted in logarithmic scale in Fig. 1. For classical, weakly coupled plasmas, relevant ND values run from 40, for the Solar atmosphere, some gas discharges, and laser produced plasmas, to 108 for the interstellar gas, while for the Solar corona and thermonuclear plasmas, they are around 10714. In addition, we have explored smaller values of ND, including some smaller than one, for which a strongly coupled plasma is expected.
Table I Initial value ρ0 at which the integration of (13) was started, and distance ρd at which tolerances of 1, 5, and 10% between the approximate and exact solutions are reached, for different values of ND.
| ρ0 | ρd | |||
| ND | 1% | 5% | 10% | |
| 0.1 | 13 | 3.569 | 2.314 | 1.828 |
| 0.3 | 11 | 2.686 | 1.510 | 1.077 |
| 1 | 11 | 1.775 | 0.734 | 0.401 |
| 2 | 11 | 1.288 | 0.368 | 0.137 |
| 5 | 7 | 0.708 | 5.11×10−2 | 1.94×10−2 |
| 10 | 5 | 0.340 | 8.43×10−3 | 7.22×10−3 |
| 40 | 5 | 1.83×10−3 | 1.40×10−3 | 1.34×10−3 |
| 1×102 | 5 | 5.51×10−4 | 4.86×10−4 | 4.71×10−4 |
| 5×102 | 4 | 8.70×10−5 | 8.05×10−5 | 7.87×10−5 |
| 1×103 | 2 | 4.02×10−5 | 3.75×10−5 | 3.68×10−5 |
| 1×104 | 2 | 3.27×10−6 | 3.10 ×10−6 | 3.06×10−6 |
| 1×105 | 0.1 | 2.77×10−7 | 2.66×10−7 | 2.63×10−7 |
| 1×106 | 0.01 | 2.41×10−8 | 2.33 ×10−8 | 2.31×10−8 |
| 1×107 | 0.001 | 2.14×10−9 | 2.08×10−9 | 2.07×10−9 |
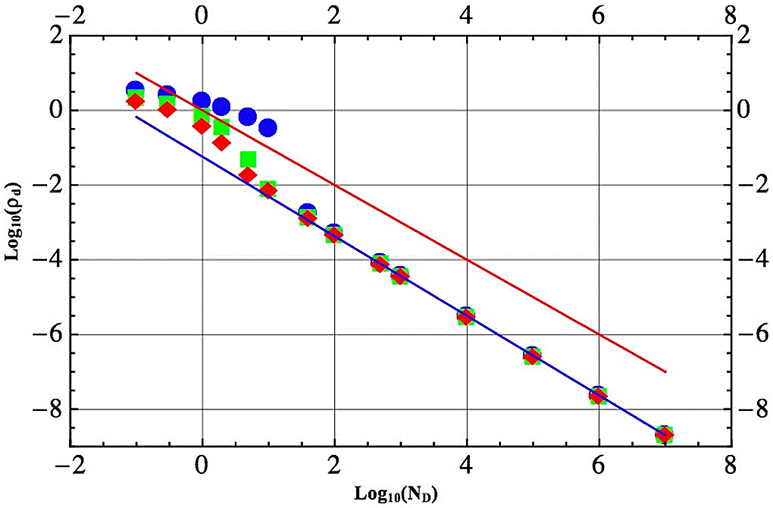
Figure 1 (In colour in the on-line version) Distances ρd at which the approximate solution breaks, for different values of N D. The blue dots are for the case in which a 1% tolerance is taken, the green squares for 5%, and the red diamonds for 10%. The blue line (below) is the fit for results that go from ND = 40 to 1×107. The red line (above) is the curve log10ρ = −log10ND.
For large values of ND, the distance values at which the approximation breaks down are very similar regardless of the tolerance. In the plot in Fig. 1, they overlap down to ND = 40. As ND is further reduced, the distance at which the approximation breaks down increases, and is larger for smaller tolerances. However, it is interesting to observe that the differences obtained for different tolerances tend to diminish for fractional values of ND. While we have followed the calculations into very small values of ND, it should be noted that the description of the charge density, used in the Poisson’s equation, in terms of a Boltzmann distribution for such a case may lose its meaning, due to the increasing importance of the temporal fluctuations about the average. Indeed, the use of the Maxwell-Boltzmann distribution assumes the particle species are in equilibrium, which requires the density to be large enough for collisions to allow relaxation to such a state.
Thus, the linear approximation is very good when ND ranges between 40 and 107, and it is possible to fit the results to the curve log10ρd = 1.18828−1.07493ND (lower line in Fig. 1), which yields the empirical law
This should be compared to the curve log10ρ=−log10 ND (upper line in Fig. 1), which stands for the limit NDρ = 1. Therefore, our result gives a quantitative meaning to the statement NDρ ≪ 1. We should note that this result differs with that found in Ref. 12:
Our work goes further than that of Ref. 12, in that we study the cases of smaller values of ND. Besides, only the case in which the tolerance is 10% was reported. We did not explore ND as large as in that previous work (1015), because it is to be expected that the approximation will improve as ND increases, while we are more interested in exploring when the approximation breaks down.
4. Conclusions
In order to study the Debye shielding, the numerical (exact) solution for the electrostatic potential Ψ(ρ) was obtained, from Eq. (13), and it was compared to the approximate solution, given by the Yukawa potential (14), found for the linearized approximation. The latter underestimates the exact solution, but is a good approximation for values of ND as small as 40. Even for ND = 5, the approximation is still good, down to r = 0.05λD if one requires only a 5% tolerance. The distances ρd, at which the approximation breaks, given fixed values of ND, for tolerances of 1, 5 and 10% were obtained, and it was observed that they are practically the same, regardless of the tolerance, for ND > 40. Using these data, the empirical law (17) was found, which gives a clear quantitative meaning to the statement NDρ ≪ 1, for the validity of the linear approximation.
From the didactical point of view, this result is illustrative of the validity of the usual approximation, which is never quantitatively explained in textbooks, even when a Maxwell Boltzmann equilibrium distribution is assumed, which may not necessarily be right in many cases.
Finally, it must be noted that the results reviewed in this paper are valid for classical plasmas, such that the distance of maximum approach rc, is much greater than the electron’s thermal wavelength











 text new page (beta)
text new page (beta)


