Introduction
Free radicals have been recognised as chemical entities in which their atomic or molecular orbitals contain unpaired electrons [1]. Reactive Oxygen Species (ROS) and Reactive Nitrogen Species (RNS), are products of normal human cellular metabolism which in low concentrations are beneficial to living systems and harmful at high concentrations. These species comprise both free radical and non-free radical oxygen containing molecules. Physiological significant ROS are the superoxide anion radical
The hydrazones have been recognized to possess various biological activities such as antioxidant [4-9], anti-microbial, anti-convulsant, analgesic, anti-inflammatory [10] anti-platelet, anti-tubercular, anti-tumoral and anticancer, antiprotozoal, antiparasitic, cardioprotective, anti-depressant, anti-HIV and trypanocidal activities [11-12].
A data set of 61 hydrazone derivatives with potent antioxidant activities based on 2, 2-diphenyl-1-picrylhydrazyl (DPPH) free radical scavenging assay was obtained from literature [4-9]. The DPPH assay is a technique that is widely employed to test the ability of compounds to act as free radical scavengers, and thus determine their antioxidant activities [13-15].
The entire data set was subjected to Quantitative Structure Activity Relationship (QSAR) studies via quantum modelling. QSAR is based on the assumption that there is an underlying relationship between molecular structure and biological activity [16]. This technique has been observed to be reliable and effective for predicting the activities and properties of untested chemical structures based on their structural similarity to chemicals with known activities and properties [17-18]. The hydrazones and their derivatives have been subjected to QSAR studies in recent time. For instance, Sahu et al, in 2012 [19], carried out quantitative structure-activity relationship (QSAR) analysis on some synthesized substituted 4- quinolinyl and 9-acridinyl hydrazone derivatives in order to find out the structural requirements of their antimalarial activities. Also, a series of novel N'-((5-nitrofuran-2-yl/4-nitrophenyl) methylene) substituted hydrazides and their derivatives have been synthesized, and tested for in vitro antimycobacterial activity, and their QSAR investigated [20].
QSAR is hereby employed in the elucidation of the structural requirements for antioxidant activities of selected hydrazones. Geometry optimization for the entire data set of 61 molecular structures was executed at the density functional theory (DFT) level using Becke's three-parameter Lee-Yang-Parr hybrid functional (B3LYP). This was combination with the 6-311G* basis set. Also, quantum chemical and molecular descriptors were calculated and subjected to data pre-treatment and normalization. The resulting data set was split into training and test sets by Kennard Stone algorithm (KSA). The training set was employed in the development of Quantitative Structure Activity Relationship (QSAR) model by Genetic Function Algorithm (GFA). Furthermore, the developed models were subjected to internal validation, external validation and y-randomization tests in order to determine their predictability, acceptability and robustness. The Variation Inflation Factor (VIF), Mean Effect (MF) and Degree of Contribution (DC) of the descriptors in the developed model were computed. Also, the applicability domain of the model was accessed by the leverage approach.
Experimental
Data Set
The 61 hydrazone data series were obtained from literature [4-9]. The antioxidant activities of the entire data set was evaluated using 2, 2-diphenyl-1-picrylhydrazyl (DPPH) free radical scavenging assay with the 50% inhibition concentrations
Geometry optimization and Descriptors calculation
The ChemDraw software [21] was employed in drawing the chemical structures of the compounds. Optimization of the molecular geometries was accomplished using Spartan 14 software (Spartan 14v112) [22] at the density functional theory (DFT) level of theory. The 6-311G* basis set was used in conjunction with the Becke's three-parameter Lee-Yang-Parr hybrid functional (B3LYP) without symmetry constraints [23]. The choice of this optimization condition lies on the fact that B3LYP/6-311G* gives excellent geometries and has the ability to make reliable estimation of the antioxidant properties of a compound [24]. A set of quantum chemical descriptors were also generated using the same software. These optimized molecular structures were later submitted for the generation of molecular descriptors using the PaDEL program package (version 2.20) [25].
Data Pre-Treatment and Normalization
Data pre-treatment was accomplished by removing descriptors having constant values and pairs of variables with correlation coefficient greater than 0.9 using "Data Pre-Treatment GUI 1.2" tool that uses V-WSP algorithm [26, 27]. Also, the entire data set after pre-treatment was normalized by scaling between the interval
Creation of Training and Test Set
The program, "Dataset Division GUI 1.2" [30] was employed in the rational selection of training and test sets from the data set of 61 chemical structures. This procedure generated the training and test sets by Kennard Stone algorithm (KSA).
Model Development
The training set compounds were employed in the development of the QSAR model.
The independent variables (quantum chemical and molecular descriptors) and the dependent (response) variables
Where
Internal Validation of the Developed Models
Methods employed in the internal validation of the developed models could be by least squares fitting method, Bootstrapping method, cross-validation (CV) method or randomization tests. In this research, the methods of cross-validation (CV) and randomization were employed. CV was carried out by leave- one- out (LOO) technique. This method involves the elimination of one compound from the data set at random in each cycle and building the model using the rest of the compounds. The activity of the eliminated compound is then predicted using the generated model. This process is repeated until all the compounds have been eliminated once.
The internal validation parameters calculated include:
The correlation coefficient, R, that measures how closely the observed data tracks the fitted regression line and thus helps to quantify any variation in the calculated data with respect to the observed data [32].
The Cross-validated squared correlation coefficient,
Where
A modification of
Where
Furthermore, the variance ratio, F value (the ratio of regression mean square to deviations mean square) was calculated using equation (5). This parameter was computed in order to judge the overall significance of the regression coefficients.
The Standard Error of the estimate (s) was calculated using equation (6).
Where
The Y-randomization test which checks the robustness of the developed QSAR model was also conducted. In this test, validation was performed by permuting the Activity (
According to Roy and Paul [35], the deviation in the values of the squared mean correlation coefficient of the randomized model (
Furthermore, Todeschini in 2010 [36], suggested a correction for
The Y-randomization results were generated using the program "MLR Y-Randomization Test 1.2" [37].
External Validation
In order to access the internal stability and predictive ability of the models, external model validation was executed. The developed models were subjected to external validation through the computation of the following external validation parameters:
The predictive R2 (R2pred) which is the predicted correlation coefficient calculated from the predicted activity of all the test set compounds. The R2pred was calculated using equation 9.
Where
Where
Also, a plot of predicted values of test set compounds against the observed values with intercept set to zero has slope equal to
Where
The program: External Validation Metric Calculator "DTC-MLR Plus Validation GUI 1.2" [(27, 42-44)] was employed in the computation of the external validation parameters.
Applicability Domain
The applicability domain for the developed QSAR model was accessed by utilizing the leverage approach [45-48]. For the calculation of the leverage value for all compounds in the dataset, the hat matrix (H) as defined in equation (14) was employed
Where
The leverage threshold, warning leverage or cut-off leverage value, h*, is the limit of normal values for
The standard residuals were calculated using equation (17):
Where
Estimation of the Variation Inflation Factor (VIF)
The variation inflation factors (VIF) was calculated using equation (18). This factor indicates the multi-collinearity, among the descriptors in the developed model.
Where
Estimation of the Mean Effect and Degree of Contribution of the Descriptors
The relative significance and contribution of a descriptor in comparison to other descriptors in the developed model is described by the magnitude and sign of its mean effect (MF). In this research, the MF for each descriptor was calculated using equation (19).
Where
Also, the degree of contribution (DC) defined as the standardized regression coefficient was calculated for each descriptor in the developed model. Computation of the DC value for each descriptor is very useful as those with high values are considered very crucial in influencing the predictivity of the developed model.
RESULTS AND DISCUSSION
The entire data set and their activities is presented in table 1. After minimization of the various compounds in the data set a total of 32 quantum chemical descriptors were generated. These were combined to the 1875 molecular descriptors which comprise constitutional, topological, Geometrical, RDF and 3D-Morse descriptors to give a total of 1907 descriptors.
Upon data processing, 1165 descriptors were produced. This overcomes the tendency of the developed model failing in its predictivity. Also, the normalized data was obtained after processing. Data Normalization reduces the tendency of any descriptor dominating the model because of larger or smaller pre-scaled value. The results of data division generated 48 molecular compounds (comprising about 80% of total compounds) in the training set and 13 compounds (comprising about 20% of total compounds) in the test set.
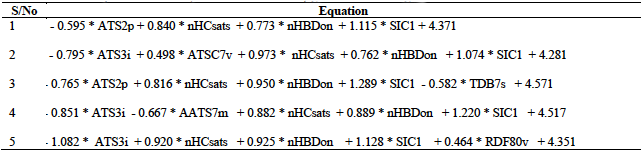
A total of five models were developed from the training set as presented in table 2. This table indicates that the minimum number of descriptors per model is four, while the maximum value is five.
The predicted activities of the training set compounds by the five developed models were also generated as presented in table S1 of the supplementary material. The predicted activities of were found to correlate appreciably with experimental activities as reflected in the results of internal validation presented in table 3.
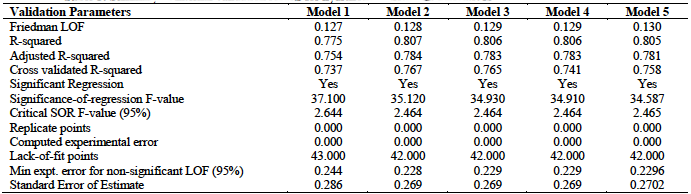
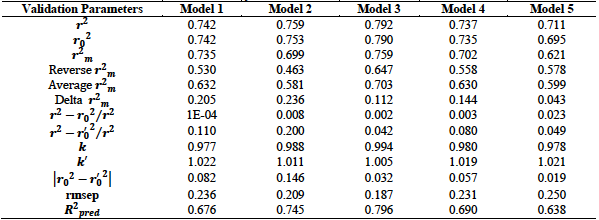
From table 3, we observe that all the five models satisfied the conditions for internal validation. Model 2 has the highest
The developed models were further employed in the prediction of the test set activities whose results are presented in table S2 of the supplementary material.
The Y-Randomization test results for the five developed models are given in table 4. These results were all within the acceptable values which stipulate that
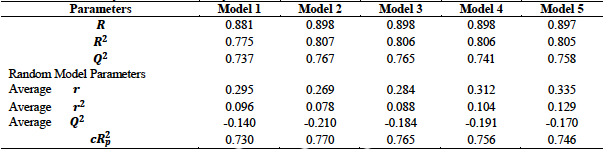
The test set compounds and their predicted activities were employed in the external validation of the developed models. External validation determines the predictive capacity of the developed models. It judges the ability of the developed models to predict the test set activity values. The results of the external validation are summarized in table 5. This result shows that the five models met all the requirements for acceptability with model 3 having the best results in terms of the external validation parameters. This model has the highest
Table 5. External validation results for hydrazone antioxidant derivatives
The acceptable threshold values for the given parameters are as follows:
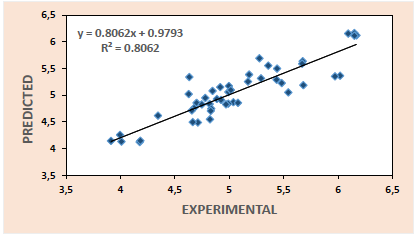
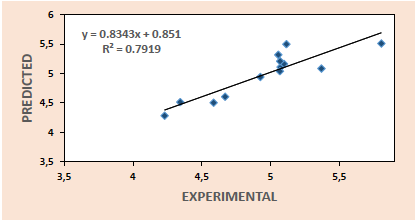
Thus, the plots of predicted activities against experimental activities for the training set (Fig. 1) and test set (Fig. 2) are generated using the results of model 3. These plots indicate very good agreement between the experimental and predicted values with impressive squad correlation coefficient
From the various validation tests conducted, we observe that all the five models generated in this research met the necessary requirements for acceptability with model 3 recording the best result. This model together with the relevant validation parameters are summarized below:
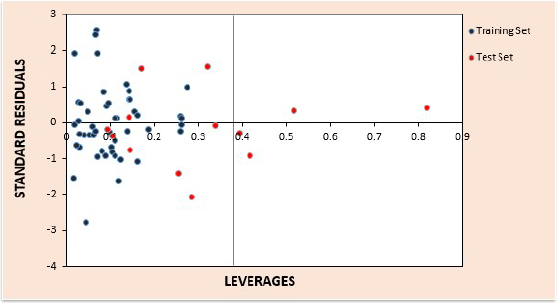
The results of applicability domain for the best developed model are given in tables S3 and S4 of the supplementary material for the training and test sets respectively. The computed value for leverage threshold, h* is 0.375. The William’s plot for estimation of the applicability domain for this model is presented in Fig. 3. In the Williams plot, the applicability domain was established inside a squared area within
The results for the computation of the mean effect (MF) variation inflation factor (VIF) and degree of contribution (DC) of the descriptors are presented in table 6.
ATS2p (Broto-Moreau autocorrelation - lag 2 / weighted by polarizabilities). This is a 2D Autocorrelation Descriptor that measures the distribution of atomic polarizability on the topology of the molecule. From table 6, the ATS2p descriptor is negatively correlated with the antioxidant activities of the hydrazone derivatives with a coefficient value of -0.76454. In terms of its degree of contribution to the developed model, it has a value of -4.39033 which actually supports its negative correlation. In terms of its degree of contribution to the developed model, it has the lowest value of -4.39033 which actually supports its negative correlation.
nHCsats
(Count of atom-type H E-State: H on C
nHBDon (Number of hydrogen bond donors (using CDK H Bond Donor Count Descriptor algorithm). This is a 2D PaDEL H Bond Donor Count Descriptor that signifies the number of hydrogen bond donors in the molecule. From the designed model, this descriptor is positively correlated with the free radical scavenging activity of the hydrazones with the highest positive coefficient value of 0.94990. Thus, increase in the number of hydrogen bond donors among the hydrazone antioxidants strongly results to an increase in their ability to scavenge free radicals. The results of DC and MF are also encouraging with values of 4.93590 and 0.55608 respectively.
SIC1 : Structural information content index (neighbourhood symmetry of 1-order). This descriptor signifies the total number of atoms of a given order that are present in a molecule. It is positively correlated with the antioxidant activities of the hidrazone with the highest values of coefficient (1.28861), MF (0.75437) and DC (7.31789) (table 6). Thus, there is good correlation in the results of the MF, DC and descriptor coefficient values for the descriptor SIC1. In comparison to the other descriptors, this descriptor recoded the highest value for these parameters. This is an indication of the strong influence of this descriptor in determining the antioxidant properties of the hydrazones. These results indicate the dominance of this descriptor as the most crucial descriptor that influence the free radical scavenging activity of the Hydrazone antioxidants. Therefore, in the design of potent antioxidants based on the hydrazine moiety, with improved activities, emphasis must be paid on this descriptor.
TDB7s (3D topological distance-based autocorrelation - lag 7 / weighted by I-state). This is a topological distance-based descriptor that also encodes information about the 3-dimenional spatial separation between atoms. The TDB7s descriptor is negatively correlated with the free radical activity of the hydrazones with a coefficient value of -0.58172. This is in agreement with the DC and MF values of -2.58458 and -0.34054 respectively. These results are the lowest in comparison with the values for the other descriptors in the developed model.
From table 6, we also observe that the highest computed VIF value is 1.65056 which corresponds to the descriptor TDB7s, while the lowest value is 1.19367 and this corresponds to the descriptor nHCsats. Thus, the computed VIF values were all greater than 1.00 and less than 5.00. This is an indication that the developed model met the requirements for acceptability since these results are within the acceptable range. Recall that when
Conclusion
This research explored the quantitative free radical scavenging activities of the hydrazone antioxidants by the application of quantitative structure activity relationship studies. Five models were developed, with model 3 chosen as the best of the five models based on its excellent validation parameters. This model indicates that Broto-Moreau autocorrelation - lag 2 / weighted by polarizabilities; Count of atom-type H E-State: H on C
Also, the results of this research demonstrate the development of a highly predictive model that can efficiently be employed in the design of new set of hydrazone antioxidants with potent free radical scavenging activities.











 nueva página del texto (beta)
nueva página del texto (beta)