Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Journal of the Mexican Chemical Society
versión impresa ISSN 1870-249X
J. Mex. Chem. Soc vol.56 no.3 Ciudad de México jul./sep. 2012
Artículo
Application of the Active Space Self-Interaction-Correction Method to Molecular Systems
Felipe Aparicio,1 Jorge Garza,2 y Marcelo Galván2,*
1 Departamento de Ciencias Naturales, División de Ciencias Naturales e Ingeniería, Universidad Autónoma Metropolitana-Cuajimalpa, Avenida Constituyentes 1054, Colonia Lomas Altas, Delegación Miguel Hidalgo, C. P. 11950 México, D. F.
2 Departamento de Química, División de Ciencias Básicas e Ingeniería, Universidad Autónoma Metropolitana-Iztapalapa A.P. 55-534 México D.F. 09340, México. mgalvan@xanum.uam.mx
Received December 11, 2011.
Accepted May 28, 2012.
Abstract
Within the context of the active space of the self-interaction-correction (SIC) optimized effective potential (OEP) method (J. Chem. Phys. 2001, 114, 639-651), the effect of the inclusion of the SIC at the level of only use the HOMO orbital is analyzed for a set of small molecules and for a model of an interstitial region surrounded by positively charged groups in a polypeptide; the model is representative of a class of regions occurring in proteins. It is shown, for the molecular systems treated in this work, that the inclusion of the HOMO orbital, within the SIC-OEP, induces a remarkable change on the eigenvalue spectrum. For the interstitial state model, the improvement is systematic as one increase the active space from one to ten orbitals; also, the influence on the local behavior of the interstitial virtual state closest to the Fermi level is important and enhances its regional character. As this method reduces the computational effort to introduce the SIC it seems promising to deal with self-interaction-corrections in systems with many atoms/electrons such as biomolecules.
Keywords: self-interaction correction, ionization potentials, HOMO-LUMO gap, excitation energies, interstitial states.
Resumen
Por medio del método de la corrección a la autointeracción (CAI) con el potencial efectivo optimizado (PEO) de espacio activo (J. Chem. Phys. 2001, 114, 639-651.), se analiza el efecto de utilizar un espacio activo que contiene sólo al orbital más alto ocupado para corregir el efecto de la auto-interacción en un conjunto de moléculas pequeñas. También se utiliza el método de espacio activo para analizar el efecto de las correcciones por auto-interacción sobre un modelo simplificado de una región intersticial con cargas positivas a su alrededor. Se demuestra que incluir sólo el orbital OMAO en el espacio activo tiene un impacto importante en el espectro de eigenvalores de las moléculas estudiadas. Por otra parte, se describe la influencia de espacios activos crecientes en el espectro de eigenvalores de un modelo de región intersticial. Se muestra que existe un efecto sistemático como función del tamaño del espacio activo en dicho espectro. Se demuestra que los efectos de la auto-interacción producen un cambio notable en el comportamiento local del estado electrónico virtual asociado con la región intersticial. Los resultados apoyan el uso de espacios activos para compensar los efectos espurios de la auto-interacción en sistemas moleculares con muchos átomos y/o electrones.
Palabras clave: corrección de la auto-interacción, potenciales de ionización, brecha OMAO-OMBD, energías de excitación, estados electrónicos intersticiales.
Introduction
The possibility of an arbitrary segmentation of the energy terms in the universal Hohenberg and Kohn functional paved the introduction of the Kohn-Sham partition in which the kinetic energy of a non-interacting system is explicitly considered; also, it is common to include explicitly the coulomb part of the electron-electron repulsion in that partition. One direct consequence of such splitting, in contrast to what happens in the Hartree-Fock theory, is the lack of an exact cancelation of the self-interaction between the coulomb part and any local or semilocal approximation to the exchange or exchange-correlation contribution. [1] That situation gives rise to a wrong asymptotic behavior in the corresponding Kohn-Sham potential. This limitation of the KS method was devised since the early stages of DFT development [2] but it was not a barrier for KS theory to become the corner stone for developing the majority of the practical applications of Density Functional Theory.
When the description of the system under study or the property of interest strongly depends on the asymptotic behavior of the KS potential, the necessity for correcting the spurious self-interaction effect emerges and several methods have been found to this end. [3] One of the simplest procedures to compensate the self-repulsion was proposed by Perdew and Zunger [2] on an orbital per orbital basis. By doing this, an orbital dependent functional is generated and in order to obtain the corresponding exchange and correlation potential of the Kohn-Sham method the use of the optimized effective potential (OEP) procedure is required.[3] Solving the OEP integral equations is quite complex but Krieger, Lee and Iaffrate figured out an approximation computationally cheaper than OEP that produces total energies and eigenvalues in close agreement to it. [4] An interesting feature of the KLI-OEP implementation of the Perdew and Zunger SIC correction (SIC-KLI-OEP) is that it allows to introduce the SIC compensation on an orbital per orbital basis. That is, one is able to generate a series of SIC corrected Kohn-Sham potentials with their corresponding eigenvalue spectra and eigenstates in which the SIC compensation includes one, two, ... etc occupied orbitals; this procedure was called "active space" self-interaction-correction method; in this context, if all occupied orbitals are included the procedure is called full SIC.[5] The main conclusions of the analysis of such series of potentials and eigenvalues spectra in atoms are the following: [5] 1) the exact asymptotic behavior of the KS potential is reached by using one orbital, the highest occupied molecular orbital (HOMO), as the active space; 2) the internal oscillations of the KS potential, related to the shell structure, are only reproduced if the orbitals belonging to the inner shell are included; 3) the full SIC eigenvalue for the HOMO orbital is almost achieved when the valence shell orbitals are included in the active space; the lowest unoccupied molecular orbital eigenvalues require a smaller active space than the HOMO to reach a closer value to the full SIC number. An appealing feature of the active space self-interaction-correction (AS-SIC) method is that it is suitable to obtain an approximate compensation of the self repulsion for any local or semilocal exchange and correlation functional at a reduced computational effort; in fact the correction to the asymptotic limit of the Kohn-Sham potential is achieved by using only the HOMO as active space and this particularly approximation is suitable for the improvement of the virtual LUMO state.
In this work, we address the AS-SIC effect on a set of small molecules and in an interstitial state typical of those that may occur in polypeptide environments. As the objective is to show the main effects induced by the compensation of the self repulsion on an orbital per orbital scheme in the systems under study, our analysis is restricted to an exchange only functional but it is important to notice that the procedure can be used with any local or semilocal exchange and correlation functional.
The rationale to test the AS-SIC method in interstitial states is related the fact that, in some cases, the folding process in proteins gives rise to the formation of positively charged regions associated to lateral chains of aminoacids such as lysine and arginine. It has been detected many of such regions in the protein data bank. [6] Also, there is recent evidence that ioniz-able groups reside stable in the inner core of proteins. [7] If the positive charged region is a sort of cavity or invagination, the LUMO band of the protein may contain interstitial states, defined as electronic virtual states associated to the cavity surrounded by positive charges rather than to a particular set of atoms. [8] The interstitial states in polypeptides share with positive defects in solids, the characteristic of being a challenge for their appropriate treatment using approximations for the exchange and correlation potential within density functional theory (DFT)-Kohn Sham methods due to the failure of an appropriate asymptotic behavior far from nuclei. [2] In addition, interstitial regions are structures involving many atoms and sometimes are in the limit of the size that is feasible to study using DFT electronic structure calculations.
The manuscript outline is as follows, in section II a summary of the AS-SIC method is presented in order to stress the orbital per orbital basis character of the method. Section III give the description of the methodology used and section IV displays the results and discussion. Finally we give in section V a summary of our findings.
The active space sic-oep approach
The self-interaction correction. Perdew and Zunger suggested an easy way to remove the self-interaction energy on any approximation to the exchange-correlation functional [2]. The idea of this SIC is quite simple because the contribution to the two-electron interaction is evaluated with each occupied orbital density, and the result is subtracted from the total exchange-correlation energy in the following way

In this equation, the  represents any approximation to the exchange-correlation functional in its spin-polarized version and J represents to the coulomb contribution. The sums in equation 1 are evaluated over the spin contribution, σ = α, β, and over the number of electrons with a defined spin, Nσ.
represents any approximation to the exchange-correlation functional in its spin-polarized version and J represents to the coulomb contribution. The sums in equation 1 are evaluated over the spin contribution, σ = α, β, and over the number of electrons with a defined spin, Nσ.
The optimized effective potential. The Perdew and Zunger proposal gives an important characteristic on the exchange-correlation contribution since now this quantity depends explicitly on each occupied orbital and consequently the associated potential will be dependent on each orbital too. In order to obtain the same potential for the occupied and unoccupied orbitals, Sharp and Horton [9], and Talman and Shadwick [10] proposed the minimization of the total energy with respect to a local potential instead of the minimization with respect to each orbital

In this equation the total energy depends explicitly on each orbital and the optimized effective potential,  , is that potential that satisfies this equation. The OEP will be a local potential if the orbitals, occupied and unoccupied, satisfy
, is that potential that satisfies this equation. The OEP will be a local potential if the orbitals, occupied and unoccupied, satisfy

Applying the chain rule on equation 2 and elements of perturbation theory we obtain

complex conjugate = 0
Because the Kohn-Sham energy, EKS, is written as

the equation 4 has the form

Inserting equation 3 in equation 6

Defining

and

equation 7 becomes as

By the definition 8, the equation 3 is written as

The Krieger, Li and lafrate approximation to the optimized effective potential equations. Krieger, Li and Iafrate (KLI) designed an approach to avoid the evaluation of the infinite sums in equation 10 [4]. With this approximation the  potential is obtained from
potential is obtained from

For the implementation of this approach it is important to take into account the restriction on the second sum in the last equation, where the HOMO is not included. The constants  are defined as
are defined as

and the  are obtained from
are obtained from

with

and

Using the KLI approximation, the procedure to find the OEP-KLI is the following. For a given set of spin - orbitals, evaluate the constants defined in equations 13 and 15 to find the average values  from equation 14. These
from equation 14. These  values are used in equation 12 to determine the OEP-KLI,
values are used in equation 12 to determine the OEP-KLI,  . With this potential, new spin-orbitals can be obtained from equation 11 and the iterative procedure continued until convergence is reached.
. With this potential, new spin-orbitals can be obtained from equation 11 and the iterative procedure continued until convergence is reached.
Details on the implementation of this approach for atoms and molecules can be found in the references [11,12].
The active space in the SIC-OEP approach. Garza et al. found that the incorporation just of the HOMO in the SIC-OEP-KLI approach ensures the correct asymptotic behavior of the exchange-correlation potential. [5] Such a conclusion was reached when one by one orbital was incorporated in the evaluation of the exchange-correlation energy and in the construction of the OEP. Thus, when the HOMO is included exclusively in this approach the equation 1 has the form

and the equation 12 becomes as

For the asymptotic region

and by using equation 16 it is obtained that

Thus, the correct asymptotic behavior of the exchange-correlation potential is obtained by using just the HOMO in the SIC-OEP-KLI approach. This is an important result since a large part of the work involved in the evaluation of equations 1 and 12 can be avoided. Naturally, when additional orbitals are included with the HOMO (active space in the SIC-OEP-KLI approach) the orbital energies are closer to the results obtained with the full SIC-OEP-KLI approach. It is worth to note that such an analysis was obtained exclusively for atomic systems and to our knowledge there is not any report where the SIC-OEP-KLI approach, coupled with the active space, is applied on molecular systems.
Computational details
All of the calculations reported in this work were done with the NWChem program [13]. In order to describe the effects of the size of active space included on the self-interaction corrections, we computed the electronic structure of a set of small organic molecules (see Table 1). Geometries of all of the molecules considered in this study were fully optimized by using the Hartree-Fock (HF) method and the Exchange only local-density approximation using the Slaters's functional (XLDA); in both cases the basis set used was the cc-pvtz. Analytic second derivative calculations, which yield the harmonic vibrational frequencies, were performed at the optimized geometries on the two levels of theory, to ensure that the optimized geometries are minima on the potential energy hypersurface (all real frequencies). To obtain the SIC, single point calculations were done with the SIC-OEP-KLI method implemented in the NWChem code. [13] The geometries came from an optimization at the XLDA/cc-pvtz level of theory; and the same basis set and exchange only functional was used in the SIC-OEP-KLI single point calculations. In order to analyze the effect of the correction including only the HOMO orbital, two different active spaces were used for the AS-SIC calculations: the first one defined by the HOMO, and the second one defined by the complete set of occupied molecular orbitals, full-SIC. As a case study for the evaluation of the self-interaction effects on interstitial states, we use the positive charged region the BgK toxin previously reported by our Group. [8] According to that we computed the electronic structure of a model of two guanidinium groups on the geometry of the Arg21 and Arg27 residues of the BgK protein. (see Figs. 1 and 2) Single point calculations of this model were done at the XLDA/cc-pvtz level of theory and using the AS-SIC procedure with the same basis set and exchange only functional. In the AS-SIC calculations, three different active spaces were used: the HOMO, the five higher occupied molecular orbitals, and the ten higher occupied molecular orbitals.


Results and discussion
In exact KS DFT theory only the HOMO eigenvalue (εHOMO) has a rigorous physical interpretation and corresponds to the negative of the first ionization potential (IP) [14,15]. It has been demonstrated that, with the SIC included in some exchange-correlation approximations, the negative of the calculated HOMO energies are much closer to the corresponding first IPs and the calculated HOMO-LUMO gaps are also closer to the first electronic excitation energies (τ) [3, 5,11,12].
Let us first focus on the HOMO energies. Table 1 summarizes the results obtained for the HOMO eigenvalue for a set of small molecules. As it is expected Hartree Fock values are quite close to the ionization potential in contrast to the exchange only LDA values that underestimate the IPs. The full-SIC and AS-SIC-HOMO approaches move the data in the right direction; and as it is seen in atoms the use of the HOMO orbital in the active space represent a large improvement. What is important to notice, is that, in addition to the large correction in each value achieved by the simplest active space, the general trend is also close to the full-SIC behavior as can be seen in figure 3. Also, one may say that the observed linear relationships between eigenvalues and experimental IPs for atoms are also present but for SIC corrected values it is not as good as for the Hartree-Fock and XLDA methods (see Fig. 4). In relation to the HOMO-LUMO gap, associated to excitation energies, the results shown in Table 2 compare this quantity with the experimental first excitation energies for the set of molecules. The calculated results are collected in Tables 1 and 2 with available experimental data. Once again, the performance of the AS-SIC-HOMO is remarkable: the correction in the numeric values, as well as the general trend, is almost equivalent to the XLDA and full-SIC results as one may conclude of the analysis of Table 2 and figure 5.


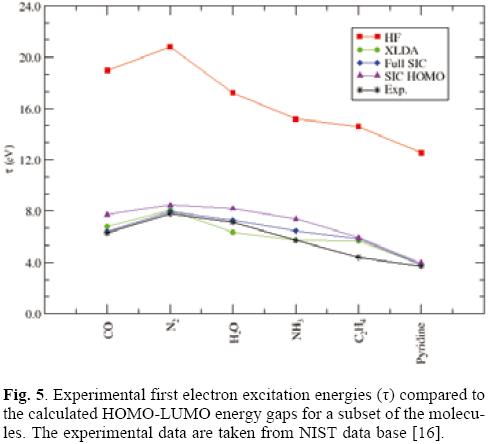
Now, let us focus on the model of interstitial states. In the case of a molecular system, the interest of using the AS-SIC approach comes from the idea to improve the description of what are called the valence molecular orbitals. Therefore, figure 6 shows the behavior of the eigenvalues of the ten highest occupied and the ten lowest unoccupied states of a system build as two interacting guanidinium groups. The effects of the size of the active space on the SIC are shown on the figure 4. If we analyze the impact of the size of the active space in the HOMO eigenvalue, one may say that including only the HOMO in the active space stabilizes the HOMO by 13.55 kcal/mol, as compared to the non corrected value; the use the five higher occupied molecular orbitals as the active space, stabilizes the same orbital by 15.19 kcal/mol; and if the active space includes the ten higher occupied molecular orbitals, the HOMO eigenvalue is shifted 22.34 kcal/mol. Also, the use of the active space with only the HOMO induces that the HOMO and HOMO-1 become almost degenerate, a situation that is mantained up to the use of an active space of ten orbitals. In relation to the LUMO eigenvalue, a similar behavior to the one observed in atoms is remarkable: the LUMO eigenvalue is less sensitive to SIC corrections.

The interstitial state in the model is the LUMO+2 orbital; its eigenvalue remains practically unchanged until the active space of five orbitals and it slightly change for the active space of ten orbitals. With respect to the local behavior, the SIC induces a significant change in the shape of the orbital. Indeed, the SIC corrected orbital behaves more as a state belonging to the intermediate region between the two charged groups.

Conclusions
As has been pointed out in section II, the use of an active space containing only the HOMO orbital is enough to ensure the correct asymptotic behavior of the Kohn-Sham potential. This will have a relevant impact in the description of the frontier orbitals in molecular systems. As a consequence of that, the trends in the IPs' and excitation energies obtained are improved and qualitatively follow the pattern of the experimental values. However, in order to obtain an appropriate description of the local behavior of the KS potential in the whole range of distances from the nuclei, the HOMO is not enough for the AS-SIC and it is necessary to include an active space of more than one orbital so that the SIC "touch" the whole valence region. For molecular systems is less clear what particular orbital has more impact when it is included in the active space and this will imply the use of the AS-SIC with a careful calibration; that is, one has to explore for each size of the active space what particular orbitals have the larger impact. The SIC procedure could be follows a localization procedure to gain efficiency in the use of a restricted number of orbitals in the active state. With respect to the use of SIC for the treatment of LUMO interstitial states, one may say that it is expected strong changes in the local behavior of such states when the SIC is included; also, the active space containing a single orbital (HOMO) could give the main correction in the eigenvalues but the impact in the local behavior remains as an open question. Due to the reduction in the computer effort to include SIC effect, the AS-SIC method seems to be a possibility to obtain reliable trends in the behavior of ionization potentials and excitation energies in molecular systems with many atoms or electrons.
Acknowledgements
We are pleased to contribute to this special issue dedicated to Prof. José Luis Gázquez Mateos. He is a trailbreaker of the development of Density Functional Theory and a builder of generations of theoretical chemists in our country. Indeed, this work is the result of collaboration between some of his academic off springs. We want to take advantage of this opportunity to thank Prof. Gázquez for his effort to promote theoretical chemistry in México. We thank to Laboratorio de Supercómputo y Visual-ización en Paralelo at UAM-Iztapalapa for giving us access to its computer facilities, and to CONACYT for financial support (contract grants 155070 and 155698).
References
1. Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules, Oxford University Press, New York 1989. [ Links ]
2. Perdew, J.P.; Zunger, A. Phys. Rev. B 1981, 23, 5048-5079. [ Links ]
3. Kummel, S.; Kronik, L. Rev. Mod. Phys. 2008, 80, 3-60. [ Links ]
4. Krieger, J. B.; Li, Y.; Iafrate, G. J. Phys. Rev. A 1992, 45, 101-126; [ Links ] Krieger, J. B.; Li, Y.; Iafrate, G. J. Phys. Rev. A 1992, 46, 54535458; [ Links ] Krieger, J. B.; Li, Y.; Iafrate, G. J. Phys. Rev. A 1993, 47, 165-181. [ Links ]
5. Garza, J.; Vargas, R.; Nichols, J.A.; Dixon, D.A. J. Chem. Phys. 2001, 114, 639-651. [ Links ]
6. No, K. T.; Nam, K. Y.; Scheraga, H. A. J. Am. Chem. Soc. 1997, 119, 12917; [ Links ] Magalhaes, A.; Maigret, B.; Hoflack, J.; Gomes, J. N.; Scheraga, H. A. J. Protein Chem. 1994, 13, 195. [ Links ]
7. Isom, D.G.; Cannon, B. R.; Castañeda, C.A.; Robinson, A.; García-Moreno E, B. Proc. Natl. Acad. Sci. 2008, 105, 17784-17788. [ Links ]
8. Aparicio, F.; Ireta, J.; Rojo, A.; Escobar, L.; Cedillo, A.; Galván, M.; J. Phys. Chem. B 2003, 107, 1692-1697. [ Links ]
9. Sharp, R.T.; Horton, G. K. Phys. Rev. 1953, 90, 317-317. [ Links ]
10. Talman, J. D.; Shadwick, W. F. Phys. Rev. A 1976, 14, 36-40. [ Links ]
11. Garza, J.; Nichols, J. A.; Dixon, D. A.; J. Chem. Phys. 2000, 112, 7880-7890. [ Links ]
12. Garza, J.; Nichols, J. A.; Dixon, D. A.; J. Chem. Phys. 2000, 112, 1150-1157. [ Links ]
13. Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T. P.; van Dam, H. J. J.; Wang, D.; Nieplocha, J.; Apra, E.; Windus, T. L.; de Jong, W. A. "NWChem: a comprehensive and scalable open-source solution for large scale molecular simulations" Com-put. Phys. Commun. 2010, 181, 1477-1489. [ Links ]
14. Janak, J. F. Phys. Rev. B 1978, 18, 7165-7168. [ Links ]
15. Perdew, J. P.; Parr, R. G.; Levy, M.; Balduz Jr., J. L. Phys. Rev. Lett. 1982, 49, 1691-1694; [ Links ] J. P. Perdew, J. P.; Levy, M. Phys. Rev. Lett. 1983, 51, 1884-1887. [ Links ]
16. NIST Computational Chemistry Comparison and Benchmark Data Base, http://srdata.nist.gov/cccbdb/default.htm [ Links ]
17. The structure corresponds to the first of the 15 deposited structures in the Protein Data Bank (http://www.pdb.org) for BgK toxin with code 1BGK. [ Links ]
18. Dauplais, M.; Lecoq, A.; Song, J.; Cotton, J.; Jamin, N.; Gilquin, B.; Roumestand, C.; Vita, C.; de Medeiros, C. L.; Rowan, E. G.; Harvey, A. L.; Ménez, A. J. Biol. Chem. 1997, 272, 4302-4309. [ Links ]
* The asterisk indicates the name of the author to whom inquires about the paper should be addressed.














