Artículo

 

GGA/PBE study of the spin isomers of Fe_34,40, Co_23,34, and Co₁₂Cu Clusters with Selected Geometries

 

Faustino Aguilera-Granja,¹ Andrés Vega,² and Luis Carlos Balbás^2,*

 

¹ Instituto de Física, Universidad Autónoma de San Luis Potosí, 78000 San Luis Potosí, México.

² Departamento de Física Teórica, Atómica y Óptica, Universidad de Valladolid, E-47011 Valladolid. Spain.

 

Received December 05, 2011.
Accepted May 23, 2012.

 

Abstract

In a recent beam deflecting experiment was found that high and low spin states of pure Fe_n and Co_n clusters with n ≤ 300 atoms coexist at cryogenic temperatures. In this work we have studied the high spin (HS) and low spin (LS) states of several structural isomers of Co₂₃, Co₃₄, Fe₃₄, and Fe₄₀ using the generalized gradient approximation (GGA) to density functional theory as implemented in the first-principles pseudo-potential code SIESTA. The calculated energy difference between these HS and LS isomers is not consistent with the observed coexistence, which can be due to an insufficient account of many body correlation effects in the GGA description, or to unknown isomer structures of these clusters. We have calculated within the same tools the magnetic isomers of Co₁₂Cu cluster aimed to re-visit a former DFT prediction of an anti-ferromagnetic ground state. We find, however, a ferromagnetic ground state as expected on physical grounds. Our results exemplify the difficulties of the current DFT approaches to describe the magnetic properties of transition metal systems.

Key words: DFT, Iron and Cobalt Clusters, Magnetism.

 

Resumen

Hemos estudiado estados magnéticos de alto y bajo espín en los agregados Co₂₃, Co₃₄, Fe₃₄ y Fe₄₀, por medio de la aproximación de gradientes generalizada a la teoría del funcional de la densidad (DFT). Nuestro propósito era explicar la coexistencia de dichos estados observada recientemente en experimentos tipo Stern-Gerlach sobre haces de agregados de Cobalto y de Hierro a temperatura criogénica. Los cálculos predicen una diferencia en la energía de esos estados magnéticos demasiado grande para que puedan coexistir a la temperatura del experimento. Esto indica que el nivel teórico no es suficiente para dilucidar estos efectos magnéticos finos, o, más probablemente, ninguna de las estructuras optimizadas corresponde a la del estado fundamental. Por otro lado, usando la misma herramienta computacional, predecimos un estado base ferromagnético para Co₁₂Cu, como cabe esperar por intuición física, mientras cálculos DFT previos predicen un estado antiferromagnético.

Palabras clave: Teoría del funcional de la densidad; agregados de hierro, cobalto y Co/Cu.

 

Introduction

Theoretical study of the magnetic isomers of transition metal (TM) clusters by means of Density Functional Theory (DFT) [1-3] is a growing issue [4-19]. Spin polarized DFT calculations yield the global magnetization of the system under study in terms of the difference between spin-up and spin-down electron densities, which are self-consistently coupled to the total electrostatic potential of the system. Self consistency is a basis requirement in the DFT search of minimum energy equilibrium structures. Thus, the total electron density is not trivially a sum of spin-up and spin-down fixed atomic densities. Although it is possible to define after a self-consistent DFT calculation the local magnetization of an atom of the system (e.g. via Mulliken population analysis), it is nothing to do with the fixed Heisenberg atomic magnets describing some systems by heuristic non first principles methods. However, that simplistic view was used recently to qualitatively explain recent experiments on spin isomers of Fe and Co clusters [20].

On the other hand, DFT is a variational approach for the ground state of a fermionic system which, in practice, relies on approximations for the unknown exchange-correlation (xc) functional describing all the many body effects. Thus, accurate DFT results arising from different xc-functionals cannot be compared systematically, in contrast to ab-initio electronic structure methods based on many body wave functions, which systematically add perturbation contributions of increasing order. Nevertheless, it has been established a hierarchy (the so called Jacob leader [4]) for the xc-functional of DFT with increasing reliability, though of limited application because it depends not trivially on the type of system under study.

In the following (1) to (5) paragraphs we briefly comment a few illustrative examples of different DFT implementations applied to the study of magnetism in TM clusters. One of these examples, the calculation of the magnetic moment of CuCo₁₂ cluster, is revised in this paper showing that a previous DFT calculation do not achieved the ground state magnetic configuration. The other part of this paper is motivated by a recent experiment determining the coexistence of high spin (HS) and low spin (LS) near degenerate magnetic states of cobalt and iron clusters [20]. That experiment cannot be interpreted in terms of Heisenberg atomic magnets, as proposed in the original paper. Instead, we perform here first-principles DFT calculations using state of the art approximations to the xc-functional.

(1) Datta and coworkers [4] have studied the relative stability of the late 3d-TM clusters with 19 atoms showing hcp and icosahedral symmetry. The plane-wave pseudo-potential method, as implemented in the Vienna ab initio simulation package () [5], and the semi-local generalized gradient approximation (GGA) [6] of Perdew-Burke-Ernzenhof (PBE) [7] for the exchange-correlation (xc) functional were employed in these calculations. It was found that Co₁₉ prefers hcp structure while Fe₁₉, Ni₁₉, and Cu₁₉ prefer icosahedral symmetry. Such behavior was attributed to the interplay between the magnetic energy gain due to high id-hybridization of hcp structures and the geometry stabilization of the icosahedral isomer.

(2) Khana and coworkers have found recently by means of DFT calculations (using PBE with the deMonk2k code [8]) that several structural isomers of Pd₁₃ exhibit different trend for their corresponding spin isomers [9]. Thus, whereas the ground state (C_s) and first isomer (C_3v) have spin magnetic moment 6 μ_B, the 134 meV less stable distorted icosahedral (~ I_h) isomer has magnetic moment 8 μ_B. Then, the observed magnetic moment 5.2 μ_B was interpreted as the thermal average of those isomers with different magnetic moments.

(3) Pradhan and Jena [10] described recently using code [5], with projector augmented wave (PAW) [11] basis set and PW91 xc-functional [12], how the magnetic coupling between Co sites in Co₂ cobalt complexes changes from ferromagnetic to anti-ferromagnetic order depending on the oxidation state (3+/4+) of the Co atoms within the several complexes.

(4) It has been also established that different xc-approaches predict different magnetic moment of Rhodium clusters [13, 14]. For example, by means of the pseudo-potential code SIESTA [15], the magnetic moment of the first isomer of Rh₆+ (triangular prism) is predicted to be 9 μ_B using PBE functional [7], but it results 5 μ_B using the recent non-local van der Waals correlation functional of Dion et al (vdW-DF) [16].

(5) The magnetic behavior of the several isomers of bimetallic Co/Cu clusters can be predicted differently depending on the DFT code. For example, Lu and coworkers [17] have investigated Co/Cu and Co/Pt bimetallic clusters with 13 atoms using the all electron Dmol3 code [18] and the GGA/PW91 xc-approximation of Wang and Perdew (PW91) [12]. They obtained that the putative ground state structures are icosahedrons. As regards the magnetic properties, these authors predicted a quite unexpected behavior. Thus, in the case of Co/Cu clusters they predicted an anti-ferromagnetic arrangement even in the limit of the Co rich phase Co₁₂Cu, with total moment of only 1 μ_B per atom, and with decreasing binding energy when the total magnetic moment increases. Since this trend is unexpected for clusters formed by late transition-metal elements (whose bulks are ferromagnetic), we have performed [19] a more systematic study of Co₁₂Cu cluster with two structures (icosahedral and biplanar), optimized via conjugate gradients algorithm, using GGA/PBE implemented in two different codes: the pseudo-potentials SIESTA code [15] and the code [5]. The latter is an all-electron method which uses the projector-augmented wave (PAW) method [11], and is supposed to be more realistic, in principle, than the pseudo-potential code SIESTA. We will discuss in detail these calculations in the subsection 3.2 below. A possible reason for the erroneous interpretation of the results of Lu et al [17] will be also given.

(6) Recent deflecting experiments on cold cluster beams in an inhomogeneous magnetic field have revealed that Cobalt and Iron clusters with up to 300 atoms present coexistence of two spin isomers having magnetic moment per atom ≈ 3 μ_B (≈ 2 μ_B) and ≈ 1 μ_B (≈ 1 μ_B) for Iron (Cobalt) respectively [20]. Previous experiments [21] did not resolve these two states but rather determine that it is the ensemble average magnetic of the high spin (HS) and low spin (LS) states that rapidly converges to the bulk value. In the new experiment the HS and LS states become degenerate for a large size, while the measured ion-ization potentials indicate that the energy gap between these two states closes with increasing size. These features were interpreted by de Heer and coworkers [20] as if the itinerant ferromagnetic state in 3d-transition metal clusters came out from two atomic states with different chemical valences. In this paper we will see that such interpretation is not supported by state of the art DFT calculations.

In this paper we present DFT results for the spin isomers of selected structures of Fe_n and Co_n clusters (n = 23, 34, 40), as well as for two structures of the Co₁₂Cu mixed cluster. In section 2 are described the computational methods. In section 3 we present and discuss our results. In subsection 3.1 we present test calculations for the choice of the atomic pseudo-potential and xc-approach to be used within the SIESTA code. It comes out that the 4s¹3d^m configuration for the pseudo-potential and the GGA/PBE approach for the xc-functional are the choices in the present work. In the subsection 3.2 are discussed the results for the Co₁₂Cu cluster, and in subsections 3.3, 3.4, and 3.5 are presented and discussed the results for Co₂₃, Co₃₄, and Fe₃₄, respectively. Section 4 contains a summary and a few conclusions.

 

Results and discussion

Computational details

The first-principles calculations were performed at the Kohn-Sham DFT level [1-3]. We have used the SIESTA code [22], with two different implementations of the exchange correlation functional: i) the well-known generalized gradient approximation (GGA), as parameterized by Perdew-Burke-Ernzerhof [7], and ii) the fully nonlocal van der Waals functional as proposed by Klimes, Bowler, and Michaelides (vdW-KBM) [23]. This functional has been implemented by Román-Pérez and Soler [24]. In the SIESTA code the core of atoms is described by norm-conserving scalar spin-dependent pseudo-potentials [25] in their fully nonlocal form [25]. Scalar relativistic and nonlocal core corrections [26] have been included. The PBE and vdW atomic pseudo-potentials for Fe and Co were generated using the configurations [Kr] 4sⁿ3d^m-n, with m = 8 for Fe and m = 9 for Co. Initially, two pseudo-potentials were generated for each element, one with n=1 and other with n = 2. For 4s, 4p, 3d, and 4f electrons the orbital core radius was the same, 2.0 Å, for both Fe and Co with n =1 and n =2, and the core correction radius was 0.7 Á for both Fe and Co.

The SIESTA code uses a flexible linear combination of numerical atomic orbitals as basis set, allowing unlimited multiple-zeta and angular momenta, as well as polarization and off-site orbitals. In order to limit the range of the basis pseudo-atomic orbitals, they are slightly excited by a common energy shift and truncated at the resulting radial node. In the present calculations we used a double-zeta polarized basis (DZP) of NAO with radii 8.0 Å for both s and d electrons. The basis functions and the electron density were projected into a uniform real-space grid in order to calculate the Hartree and exchange-correlation potentials and matrix elements. The grid fineness is controlled by the energy cutoff of the plane waves that can be represented in it without aliasing (250 Ry in this work). The electronic temperature (smearing) was 25 meV. All structures were optimized up to the forces on atoms were smaller than 0.006 eV/Å.

Among the explored xc-functional flavors, the vdW-DF one deserves particular attention. In particular the KBM flavor has proven to be superior to others vdW-DF for the prediction of electronic properties of metallic systems, like the dipole moment and polarizability of sodium [28], cesium [29], and gold/mercury [30] clusters, as well as the bulk of these and other metals [31]. The vdW-DF functional is based on the work of Dion and coworkers [16] who demonstrated that the vdW interaction can be expressed by a nonlocal functional depending only on the electron density. After that work, numerous efforts have been developed to include vdW forces within DFT [32]. Dion and coworkers proposed to divide the exchange-correlation energy in three parts:

E_xc[n(r)] = E_x^GGA[n(r), |∇n(r)|] + E_c^LDA[n(r)] + E_c^nl[n(r)]

where

E_x^GGA = ∫d³r n(r) ε_x^GGA[n(r), |∇n(r)|]

is the exchange energy functional described originally [Dion] through the semilocal generalized gradient approximation functional of Zhang and Yang [33], and more recently Klimes et al [21] used an optimization of the Becke functional (B88) [34]. The expression

E_c^LDA = ∫d³r n(r) ε_c^LDA[n(r)]

is the correlation energy described in the local density approximation (LDA) parameterized by Perdew and Zunger [34], and E_c^nl [n(r)] is a nonlocal contribution to the correlation energy which contains the dispersion interaction, given by

E_c^nl [n(r)] = ½∫∫d³r₁ d³r₂ n(r₁) n(r₂) Φ(q₁,q₂,r₁₂)

where r₁₂ = |r₁ - r₂|, and q₁, q₂ are the values of a universal function q[n(r),|∇n(r)|],

q(n, |∇n|) = [1 + ε_c^LDA/ε_x^LDA + (0.8491/9)( |∇n|/2nk_F)²]k_F

evaluated at r₁ and r₂. The kernel Φ has also a precise and universal form that in fact depends only on two variables, d₁ = q₁r₁₂ and d₂ = q₂r₁₂, but it can be written also as a function of q₁, q₂, and r₁₂. As a matter of fact, it is written in terms of D = (q₁+q₂)r₁₂/2 and δ = (q₁ - q₂)r₁₂/2, and then it can be shown that: (i) E_c^nl is strictly zero for any system with constant density; and (ii) the interaction between any two molecules has the correct r^-6 dependence for large separations.

Due to the high computational cost to self-consistently evaluate the E_c^nl term, applications of this functional are still scarce. Nevertheless, Román-Pérez and Soler [24] have performed a very efficient self-consistent implementation of vdW-DFT functional in the SIESTA code, which allows [15] to simulate large systems with small additional cost as compared to LDA or GGA calculations.

In this work, the initial geometries were selected among those low lying isomers of Fe_n and Co_n giving in the Cambride Cluster Data Bases [36]. These structures were obtained from an extensive search for the Global Minimum geometries based on a Gupta empirical potential, with subsequent re-optimization of many candidate structures. Our equilibrium geometries were obtained from unconstrained conjugate-gradients structural relaxation using DFT forces. The structures were relaxed until the force on each atom was smaller than 0.01 eV/Å. Benchmark tests of the 4s²3d⁶ and 4s¹3d⁷ pseudo-potentials for GGA/PBE and vdW/KBM xc-functional for Fe atom and Fe bcc bulk, as well as for Fe₃₄ and Fe₄₀ clusters, are presented and discussed in subsection 3.1.

 

Test of pseudo potentials

The binding energy, E_b(M_n), of a cluster M_n with n atoms (M = Fe, Co, in this paper) is defined as E_b(M_n) = nE(M) - E(M_n), where E(M) and E(M_n) are the total energy of the M atom and M_n cluster, respectively. Thus, E_b is a positive quantity for stable clusters, that is, the cluster formation is an exothermic process. The binding energy per atom can be also called the cluster cohesive energy because its analogy with the definition of cohesive energy in bulk systems. Both names for the same concept will be used indistinctly along this paper. Note that the total energy difference between isomers is the same than the difference in their binding energies.

The importance of obtaining good atomic reference energies to calculate the binding energy of 3d-TM systems in local density approximation (LDA) [2] and GGA/PW91 [12] approaches was studied by Philipsen and Baerends [37]. They found that the effect of non-spherical charge distributions is larger for GGA than for LDA, particularly for iron. Instead, allowing fractional occupations of 3d and 4d shells has negligible effects in both approaches. It was shown that GGA improves over the LDA binding energy of 3d systems only if the lowest energy single determinant state for the atoms, without symmetry restrictions, is used to obtain the atomic reference energy. The restriction to integer occupation numbers was proved to have negligible influence on the GGA atomic energies [37]. In spherical symmetry the energy lowering is primarily due to spin polarization, although in some cases (Ti, V, Co, Ni) there is also a change of configuration (from dⁿs² to dⁿ⁺¹s¹). The multiplet method of Ziegler et al to calculate degenerate atomic ground states, is applicable to TM-atoms by identifying among the ground states the one which is a pure state function obeying the Hund's rules: the lowest-energy term of a configuration is the term with maximum L selected from all terms of maximum spin multiplicity, that is, the determinant with maximum M_L and M_S.

We have constructed scalar relativistic non-local atomic pseudo-potentials for Fe and Co from the configurations [Kr] 4sⁿ3d^mn, with m = 8 for Fe and m = 9 for Co, in both, GGA/ PBE and vdW/KBM approaches. For both values n = 1 and n = 2 Hund's rule of maximum total spin polarization, lead to a magnetic moment 4 μ_B (3 μ_B) for Fe (Co), since in DFT s and d electrons are considered. Instead, if s electrons does not contributes any magnetic moment, as assumed by de Heer [20, 21] (see section 1 above), these configurations should produce 4 μ_B (3 μ_B) for n = 2 (n = 1) in atomic Fe, and 3 μ_B (1 μ_B) for n = 2 (n = 1) in Co. We have constructed also two relativistic spin dependent pseudo-potentials from the configurations [Kr] 4s²3d↑^r 3d↓^q with r + q = 6 for Fe and r + q = 7 for Co. The putative Hund's rule magnetic moment of Fe for r = 4, q = 2 is 2 μ_B, and for r = 5 q = 1 it is 4 μ_B. The calculated ionization potentials for the Fe relativistic vdW/KBM pseudo-potentials [Kr] 4s¹3d⁷ and [Kr] 4s²3d⁶ are 8.46 eV and 7.69 eV, respectively. For the corresponding GGA/PBE pseudo-potentials we obtain 8.36 eV and 7.44 eV, respectively. Comparing these values with the experimental ionization potential (IP), 7.87 eV, we see that the [Kr] 4s²3d⁶ relativistic pseudo-potentials for both KBM and PBE approaches lead to the best agreement.

In figure 1 we compare the binding energy per atom for three iron systems (Fe₃₄ (D_5h), Fe₄₀ (D_6h), and bulk (bcc)) optimized within GGA/PBE and vdW/KBM approaches. In both cases we have tested two scalar relativistic pseudo-potentials for Fe, namely, those constructed with the configurations [Kr]4s²3d⁶ and [Kr]4s¹3d⁷, respectively. We see that the [Kr]4s²3d⁶ pseudo potential leads to larger (smaller) binding energy for clusters (bulk) than the [Kr]4s¹3d⁷ one. The vdW/KBM approach leads to slightly higher binding energy than GGA/PBE one, except for bulk bcc Fe with the [Kr]4s¹3d⁷ pseudo-potential configuration. However, in that case we obtain the better agreement with the experimental cohesive energy. Since a good description of the cohesive energy is crucial for the present work, we will use the [Kr]4s¹3d⁷ pseudo-potential of atomic Fe in the remaining of this work. As the binding energy difference between GGA/ PBE and vdW/KBM calculations is very small, we will use in the following the GGA/PBE, which demands less computational resources than the vdW/KBM approach.

 

Spin isomers of Co₁₂Cu

As quoted in the Introduction (Section 1), Lu et al [17] have predicted in the case of Co/Cu clusters an anti-ferromagnetic arrangement even in the limit of the Co rich phase Co₁₂Cu. For this cluster they obtained a total moment of only 1 μ_B per atom, as well as magnetic isomers with decreasing binding energy when the total magnetic moment increases. We comment now the results of our calculations using the methods described in section 1 above.

First of all, we have calculated the spin isomer of Co₁₂Cu imposing a total spin of 1 μ_B per atom. This state, due to the formation of anti-parallel magnetic couplings between Co atoms, has a considerable lower binding energy than the calculated state with total moment 2 μ_B per Co atom and parallel couplings (the ferromagnetic-like configuration). The difference of total binding energy between both self-consistent magnetic solutions, obtained with both codes and the same xc-functional used by Lu et al [17] (the so called PW91 [12]) results to be larger than 1 eV. This is at odd with Lu et al's predictions, although they do not report data for the ferromagnetic solution.

The next step was to perform calculations for other low spin isomers to try to find a clear picture of the possible antiferromagnetic excitations of this cluster. Once verified that SIESTA/PBE, /PBE and /PW91 gave essentially the same results, we selected SIESTA/PBE for these calculations due to the lower computational requirements as compared with , and also for the sake of comparison with the rest of results reported in the present work. In figure 2 we plot the binding energy as a function of the total magnetic moment of Co₁₂Cu. The curve shows that all anti-ferromagnetic states are magnetic excitations of the ground state with 23 μ_B and ferromagneticlike order. However, it is interesting to note a non-monotonic behavior as a function of the total spin, with a minimum of the binding energy obtained for a total spin moment of 11 μ_B. This means that some anti-ferromagnetic excitations, with rather compensated moments and correspondingly weak total magnetization, result more accessible than others with larger total moment. This unexpected trend was found by Lu et al.[17] for the four spin isomers with lowest total moment. We stress, however, that the ground state is ferromagnetic, and that the lowest energy spin isomers are those with a large total moment and a small degree of anti-ferromagnetic order (only few atoms with their moments coupled anti-parallel). Some comments are also pertinent in regard to the lowest energy structural configuration proposed by Lu et al [17]. SIESTA calculations predict a bi-planar structure as the lowest energy one for Co₁₃ among those tested, including the icosahedrons. This bi-planar structure has been also predicted for Co₁₃ in a recent work by Dong and Gong [38] using and results from the one found in the present work for the 12 atoms clusters plus an additional atom in. The difference in binding energy with respect to the icosahedral structure is about 1 eV. We guess that this biplanar structure resulted probably a high-energy isomer in the genetic algorithm used by Lu et al. based on the Gupta potential, as it is well known that Gupta tends to favor spherical structures, in particular icosahedral ones. Nevertheless, our calculations give the same ground state ferromagnetic configuration for this structure and for the icosahedral one.

 

C0₂₃

In the low panel of figure 3 are shown the geometries of ten atomic arrangements of Co₂₃ cluster which have been optimized using GGA/PBE approach for the high spin (HS = 2 μ_B) and low spin (LS = l μ_B) magnetic configurations. The corresponding binding energies per atom are represented in the upper panel of figure 3. All the HS isomers have ferromagnetic order, but the LS isomers show partial anti-ferromagnetic order. The more stable HS isomer shows star-like (D_5h) geometry, with binding energy per atom about 21~23 meV higher than those HS isomers with planar and poli-icosahedral arrangements. Except the bi-planar bbp isomer, all the HS configurations in figure 3 have binding energy per atom in a window ~ 70 meV. The binding energy per atom of the LS state of a given geometry is always smaller than the HS one, which is ferromagnetic. However, the stability of LS isomers follows a different sequence of geometries than the HS solutions. The smaller binding energy difference between HS and LS isomers occurs for the bcc and fcc-like configurations, ~ 145 meV. However, the HS state of these isomers is ~ 45 meV. Thus, if HS and LS states coexist in the beam experiments of de Heer et al. [20], they should surpass ~ 190 meV per atom which allows coexistence of several geometries with HS ferromagnetic state. Then, our calculations cannot explain the experimental fact, due, probably, to inaccuracy of the theoretical approach, or lack of the ground state isomer.

 

C0₃₄

In figure 4 are represented the binding energies of four Co₃₄ arrangements for two magnetic configurations, namely ferromagnetic (2 μ_B per atom) and anti-ferromagnetic (2 μ_B per atom). Similar considerations to that noted above for Co₂₃ isomers can be done, but now the barrier between magnetic states is even larger.

We have calculated the ionization potential of hcp Co34 for HS and LS magnetic states, with the results 6.08 eV for HS state and 5.60 eV for LS state. These values are a little bit higher than those reported by de Heer et al [20], ~5.58 eV (HS) and ~5.40 eV (LS).

 

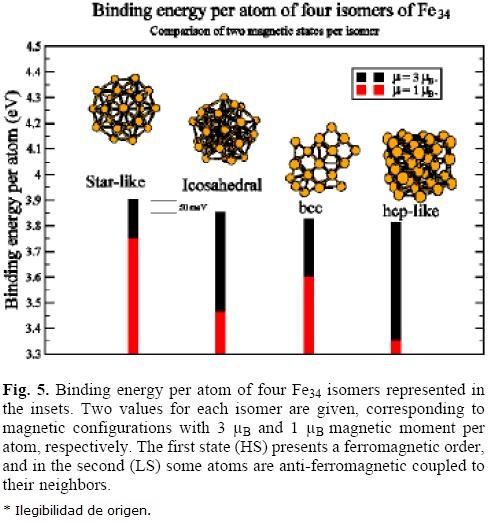
Fe₃₄

In figure 5 is represented the binding energy per atom of the HS (3 μ_B) and LS (1 μ_B) magnetic isomers of four configurations of Fe₃₄ cluster optimized within the GGA/LDA approach. The more stable geometry of the HS isomers is the start-like (D5h), and the other geometries are less stable by about 50-60 meV per atom. The binding energy of the start-like LS isomer is about l50 meV smaller that the HS one and that difference is larger for the other geometries. Thus, we can be sure than none of these arrangements fulfill the requirement of magnetic isomers observed in the de Heer et al experiment.

 

Conclusions

We have used the first principles code SIESTA to self-consis-tently solve the spin-polarized Kohn-Sham equations of DFT theory for the spin isomers of pure Fe₃₄, Fe₄₀, Co₂₃, Co₃₄ and mixed C0₁₂Cu transition metal clusters. For the choice of atomic-pseudopotential we have tested two flavors of the xc-functional, the semi-local GGA/PBE and the more recent vdW-DF/ KBM which contains a fully non-local correlation functional taken into account long rang van der Waals interactions. For Fe clusters, two atomic norm-conserving relativistic pseudo-potentials were also tested, with valence configurations 4s¹3d⁷ and 4s²3d⁶. According to these tests, we chose the GGA/PBE xc-approach, because is computationally less expensive than the vdW-DF one, and the 4s¹3d⁷ (4s¹3d⁸) pseudo-potential for Fe (Co) because it leads to better agreement with experimental bulk cohesive energy.

Firstly, we obtain that the ground state of CuCo₁₂ mixed cluster is ferromagnetic with magnetic moment 23 μ_B and biplanar geometry. The icosahedral isomer is also ferromagnetic with magnetic moment 23 μ_B in contrast to the anti-ferromagnetic state predicted in a previous study [17].

Second, we have calculated the binding energy of selected geometries of Co₂₃, Co₃₄, and Fe₃₄ clusters with the HS and LS states detected in the de Heer experiments [20]. The calculated binding energy difference between these spin states is too large, and then their coexistence in the beam at cryogenic temperatures should not occur. We conclude that either the GGA/PBE is not enough accurate or the tested geometries are far from the true ground state isomer. Then, for this problem it is needed one or more of the following conditions: i) a more accurate code (for example an all-electron DFT code without pseudo-potentials), ii) a xc-functional beyond the GGA/PBE approximation, and iii) a search of the global minimum structure of these clusters from first principles.

The coexistence of HS and LS states of Cobalt and Iron clusters which was found in recent experiments by de Heer et al [20] cannot explained by a simplistic model of atomic magnets. Specifically, these authors proposed that the Co_n and Fen observed ground state magnetic moments are due to atomic electronic orbital configurations 3d↑⁵3d↓³4s¹ for Co and 3d↑⁵3d↓²4s¹ for Fe, leading to spin states (considering that only the d electrons contributes) S = 1 (μ = 2 μ_B ) for Co_n and S = 3/2 (μ = 3 μ_B ) for Fe_n clusters. Instead, the observed excited states are also Heisenberg magnets with atomic configurations 3d↑⁵3d↓⁴4s⁰ (S = ½, μ = 1 μ_B) for Co* and 3d↑⁴3d↓³4s¹ (S = ½, μ = 1 μ_B) for Fe*. Contrary to that simplistic proposal of de Heer [20] based on atomic valence configurations of Fe and Co whose 4s electrons have no spin, DFT calculations shows that all the occupied orbitals contribute to the total spin through the self-consistent xc-potential of the spin polarized formulation of DFT. Thus, the accurate account of the de Heer experiments [20] is a challenge for future DFT developments, both theoretical and methodological. Practical methods for the search of the global minimum structure of transition metal clusters are also needed.

 

Acknowledgements

We acknowledge the support of the Spanish "Ministerio de Ciencia e Innovación", the European Regional Development Fund and "Junta de Castilla y León" (Grants Nos. FIS2011-22957 and VA104A11-2). F.A-G acknowledge the financial support from PROMEP-SEP-CA230, 162651 and the Ministerio de Educación cultura y Deporte (SAB2011-0024, Spain). F.A-G acknowledges a grant of University of Valladolid, where part of this work was performed.

 

References

1. Hohemberg, P.; Kohn, W. Phys. Rev. 1964, 136, B864-B871.         [ Links ]

2. Kohn, W.; Sham, L. Phys. Rev. 1965, 140, A1133-A1138.         [ Links ]

3. von Barth, U.; Hedin, L. J Phys C 1972, 5, 1629.         [ Links ]

4. J.P. Perdew, J. Chem .Theor. Comp. 2009, 5, 902-908.         [ Links ]

4. Datta, S.; Kabir, M.; Saha-Dasgupta, T. Phys. Rev. B, 2011, 84, 075429/1-7.         [ Links ]

5. Kresse G.; Furthmüller J. Phys. Rev. B, 1996, 54, 11169.         [ Links ]

6. Becke, A. D. Phys. Rev. A 1988, 38, 3098;         [ Links ] Perdew, J. P. Phys. Rev. B 1986, 38, 3098.         [ Links ]

7. Perdew, J. P.; Burke, K.; Ernzerhof, M. Phys. Rev. Lett. 1996, 77, 3865-         [ Links ].

8. http://www.deMon-software.com        [ Links ]

9. Köster, A. M.; Calaminici, P.; Orgaz, E.; Roy, D. R.; Reveles, J. U.; Khanna, S. N. J. Am. Chem. Soc., 2011, 133, 12192-12196.         [ Links ]

10. Pradhan, K.; Jena, P. Appl. Phys. Lett. 2011, 99, 153105/1-3.         [ Links ]

11. Kresse G.; Joubert D. Phys. Rev. B 1999, 59, 1758.         [ Links ]

12. Wang, Y.; Perdew, J.P. Phys. Rev. B 1991, 43, 8911.         [ Links ]

13. Aguilera-Granja, F.; Balbás, L. C.; Vega, A. J. Phys. Chem. A 2009, 113, 13483-13491.         [ Links ]

14. Torres, M. B.; Aguilera-Granja, F.; Balbás, L. C.; Vega, A. J. Phys. Chem. A 2011, 115, 8350-8360.         [ Links ]

15. Soler, J. M.; Artacho, E.; Gale, J. D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. J. Phys.: Condens. Matter, 2002, 14, 2745-2779.         [ Links ]

16. Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D. C.; Lundqvist, B. I. Phys. Rev. Lett. 2004, 92, 246401/1-4.         [ Links ]

17. Lu, Q. L.; Zhu, L. Z.; Ma, L.; Wang, G.H. Chem. Phys. Lett. 2005, 407, 176.         [ Links ]

18. Accelrys.com        [ Links ]

19. Aguilera-Granja, F.; Torres, M. B.; Vega, A.; Balbás, L. C. J. Phys. Chem. (DOI:10.1021/jp306353b).         [ Links ]

20. Xu, X.; Yin, S.; Moro, R.; Liang, A.; Bowlan, J.; de Heer, W. A. Phys. Rev. Lett. 2011, 107, 057203/1-4.         [ Links ]

21. Billas, I. M. L.; Chatelain, A.; de Heer, W. A. Science, 1994, 265, 1682.         [ Links ]

22. Klimes, J.; Bowler, D. R., Michaelis, A. J. Phys.: Condens. Matter, 2009, 22, 022201.         [ Links ]

23. Soler, J. M.; Artacho, E.; Gale, J. D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. J. Phys: Condens. Matter 2002, 14, 2745.         [ Links ]

24. Román-Pérez, G.; Soler, J. M. Phys. Rev. Lett. 2009, 103, 096102.         [ Links ]

25. Troullier, N.; Martins, J. L. Phys. Rev. B 1991, 43, 1993.         [ Links ]

26. Kleinman, L.; Bylander, D. M. Phys. Rev. B 1982, 48, 1425.         [ Links ]

27. Louie, S. G.; Froyen, S.; Cohen, M. L. Phys. Rev. B 1982, 26, 1738.         [ Links ]

28. Aguado, A.; Vega, A.; Balbás, L. C. Phys. Rev. B 2011, 84, 165450/1-10.         [ Links ]

29. Aguado, A. J. Phys. Chem. C 2012, 116, 6841-6851        [ Links ]

30. Fernández, E.; Balbás, L. C. Phys. Chem. Chem. Phys. 2011, 13, 20863.         [ Links ]

31. Klimes, J.; Bowler, D. R., Michaelis, A. Phys. Rev. B, 2010, 83, 195131.         [ Links ]

32. See, i.e., A. Becke, A.; Johnson, E. R. J. Chem. Phys. 2007, 127, 154108.         [ Links ]

33. Zhang, Y.; Yang, W. Phys. Rev. Lett. 1988, 80, 890.         [ Links ]

34. Becke, A. D. Phys. Rev. A 1988, 38, 3098.         [ Links ]

35. Perdew, J.; Zunger, A, Phys. Rev. B 1981, 23, 5048.         [ Links ]

36. The Cambridge Cluster Database, http://www-wales.ch.cam.ac.uk/CCD.html        [ Links ]

37. Philipsen, P. H. Y.; Baerends, E. J. Phys. Rev. B 1996, 54, 5326.         [ Links ]

38. Dong, C.D.; Gong, X.G. Phys. Rev. B 2008, 78, 020409(R).         [ Links ]

 

Note

* The asterisk indicates the name of the author to whom inquires about the paper should be addressed.