1. Introduction
With the arrival of the twenty-first century, population aging has become increasingly significant. Functional abnormalities of lower limb mobility are caused by a variety of diseases and traumas. The lower limb aided exoskeleton robot is a wearable human-computer integrated device that can accomplish a variety of high-intensity tasks using human lower limb guiding (Zhang et al., 2020). Using a hybrid control method comprising position control and sensitivity amplification control, a Berkeley University of California research team built a lower extremity exoskeleton robot (BLEEX) (Huo et al., 2020). The findings reveal that the lower limb rehabilitation exoskeleton will work out alongside the wearer. The State Key Laboratory of Fluid Transmission and Control at Zhejiang University developed an exoskeleton that uses fuzzy logic analysis and decision making to determine the wearer's movement intention in (Sun et al., 2019a). Shanghai Jiaotong University uses the fuzzy adaptive PID (proportion integral). The use of a derivative control algorithm on a hybrid lower limb exoskeleton robot boosts the human body's load capacity. Many controlled objects in actual control systems, such as robot control systems, are nonlinear, and the motion process includes repetition, as we all understand.
Although we aim to thoroughly comprehend the properties of the controlled item in the actual control in order to get an accurate mathematical model to realize accurate motion control, due to the system's complexity, this is difficult to do. The nonlinear system can be controlled using PID control, which is frequently utilized in the industrial industry. However, adjusting PID parameters can take a long time, and it may not result in a satisfactory control effect or control efficiency (Sun et al., 2019b).
Despite the fact that several types of lower knee rehabilitation have been developed by researchers, few exoskeletons are acceptable for patients with all stages of injury. The majority of suspended gait trainers are designed for patients who are able to stand up and are in the middle or late phases of their recovery. Stroke patients would recover more quickly if they began rehabilitation training sooner after the illness had stabilized (Sale et al., 2014). As a result, the rehabilitation trainer who specializes in sitting and lying has a distinct edge. Bio-signal based control, position tracking control, force and impedance control, and adaptive control are the four primary groups of control systems that have been reported in the literature (Meng et al., 2015). Position tracking control is the foundation of other systems for rehabilitation robotic exoskeleton control. It is critical to achieve continuous and repetitive training by employing high-precision control algorithms (Chen et al., 2016). To supplement the disturbance management of a traditional proportional-derivative (PD) control law, a particle swarm optimized active force control technique is developed. According to the simulation results, the suggested control strategy effectively mitigates the disturbance effect while preserving tracking performance, which appears to be in sharp contrast to its standard PD counterpart (Majeed et al., 2017).
The lower limb exoskeleton robot's servo control model is established using the iterative learning control (ILC) algorithm in (Guan et al., 2021), and the exponential gain closed-loop system is designed using MATLAB software. Because of its model independence and great self-learning ability, the ILC technique is well suited for the control of such periodic nonlinear systems, laying the groundwork for ILC's rapid evolution. In real life, there is no such thing as an ideal atmosphere free of distractions. For better performance, current disruptions must be corrected. The basic goal of ADRC is to treat internal and external uncertainty as a whole and to actively eradicate them (Li et al., 2016). The ADRC technique does not necessitate a thorough understanding of the dynamics and divides the plant into a number of disrupted systems that are calculated online and then properly cancelled. Furthermore, any prior dynamical system knowledge can be included into the ADRC design (Gao, 2006; Humaidi & Badr, 2018). The so-called extended state observers (ESOs) can estimate the entire disturbance in the plant (Xing et al., 2013). Because the ADRC's performance is determined by the ESOs' gain selection, it is vital to modify parameters and acquire accurate estimates to minimize undesirable effects (Abdul-Adheem et al., 2020; Ball & Khalil, 2008). The proposed ADRC approach has the potential to deliver good tracking performance while also dealing well with disturbances. Han demonstrated that ADRC may replace PID strategy with unmistakable performance and practicality, as well as provide remedies for difficulties arising from disturbances (Han, 2009). The ADRC strategy, on the other hand, is reported to have been utilized in the rehabilitation system's establishment.
The ADRC approach is used in this research to drive the lower extremity exoskeleton to follow the clinical trajectory of a human. The ESO is used to estimate the disturbances in the dynamics model online using a mathematical model of the human exoskeleton. The ADRC control law is obtained using the estimated disturbances. To establish that the ADRC approach is stable and correct, simulations are run in MATLAB. Experiments with genuine exoskeletons have been carried out, and the findings show that the LADRC technique outperforms the NADRC strategy. It is a revolutionary way to use the LADRC strategy to replace the traditional position control strategy in the rehabilitation exoskeleton, particularly when there are external disruptions.
The rest of the paper is organized in many sections. The second section discusses the human-exoskeleton rehabilitation mechanism and modeling. In the third section, the proposed control plan approaches are constructed. The fourth segment contains optimization ADRC parameters simulations. Results analysis and discussion are showed in fifth section. In the concluding portion, conclusions are formed.
2. Human-exoskelton system
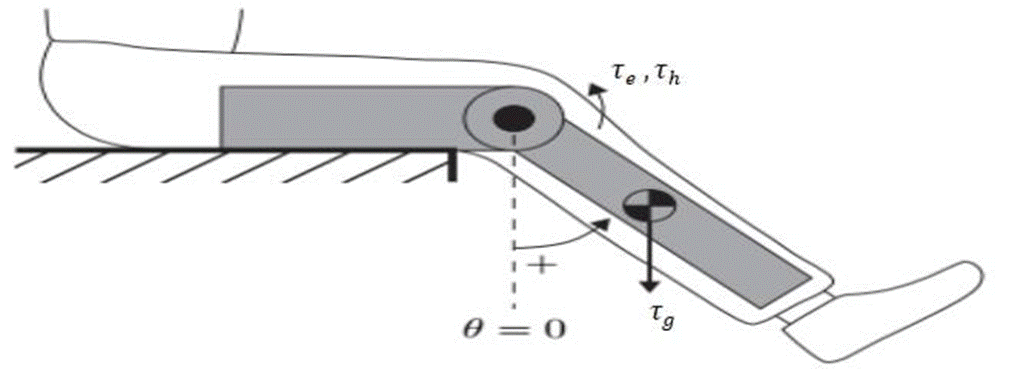
A model can be expressed as (Mefoued & Belkhiat, 2018; Sherwani et al., 2020) for a 1-DOF lower limb exoskeleton helping knee flexion and extension in a planar seated posture (see Figure. 1).
Where J is the lumped inertia of the human and exoskeleton shank-foot, B is the lumped viscous friction parameter, A is the solid friction parameter, τg is the lumped gravitational torque, τ and τh are the exoskeleton and human torques, respectively. Because the exoskeleton and the wearer's joints are securely connected in the model, knee extension and flexion movements are deemed synchronous and simultaneous (Huo et al., 2019). J, A, B, and τg are unknown model parameters that were discovered empirically as stated in ref. (Mefoued & Belkhiat, 2018) and shown in Table 1. The exoskeleton for the knee joint is designed to provide power assistance during rehabilitation. It is made up of two pieces, a thigh and a shank, with the former attached to a fixed surface and the latter to the human shank, both of which are held together by comfortable yet secure braces. The braces adjust along a rail to fit each individual, reducing misalignment between the exoskeleton and human knee joint. Human model parameters account for minor changes in the system attributes. A high-power DC motor provides torque at the knee joint level.
Table 1 Shows systems identified parameters.
| parameter | value |
|---|---|
| Inertia (J) | 0.484 Kg.m2 |
| Solid Friction | 1.321N.m |
| Coefficient (A) | |
| Viscous Friction | 0.751 N.m.s./rad |
| Coefficient (B) | |
| Gravity Torque (τg) | 3.877N.m |
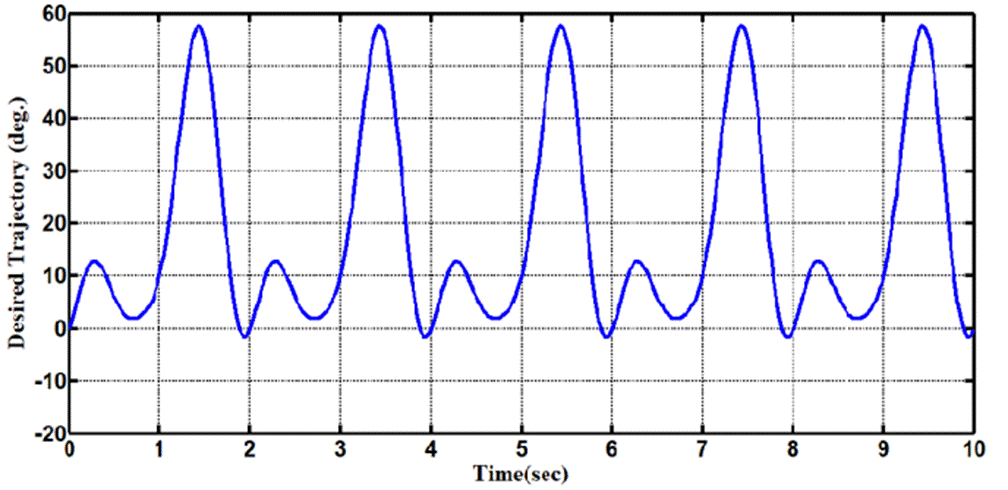
The exoskeleton allows the patient to move in the well- known preset trajectory to initialize joint motions in the early stages of rehabilitation and in passive mode. The goal of the rehabilitation exoskeleton in this study is to accurately recreate the walking pattern under the effect of noise and disruptions. The trajectories for the knee joint are calculated using a fitting expression and clinical gait analysis data; see ref. (Bov et al., 2011; Long et al., 2017) for more information. This clinical path is depicted in Figure 2.
3. ADRC methodology
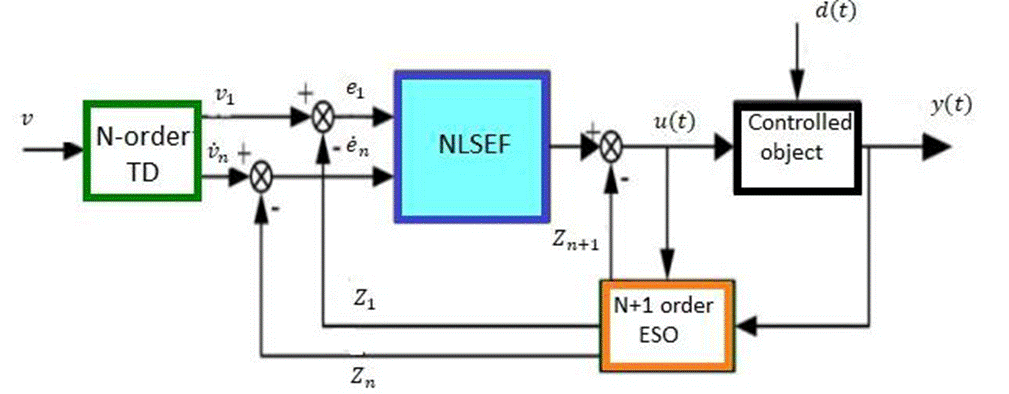
In general, the ADRC technique, which combines LESO, TD, and LPD eliminates the system's unmolded dynamics and uncertainties, enhances its dynamic responsiveness, and meets all design requirements (Abdul-Adheem et al., 2021; Gao, 2006). The general block diagram of the Han ADRC technique is shown in Figure 3.
3.1. LADRC
All of the ADRC components are linear here: (TD), (LPD), and (LESO). To avoid overload and maximize system performance, the TD is widely utilized. The structure equation of a second order TD is works with a transient profile of input signals that has been differentiated to avoid abrupt shifts, resulting in a progressive increase in output rather than sudden increases.
Where (V) is the desired trajectory and (
Where (e) is the error and the gains (Kp, Kd) are calculated as:
Where (wc) is controller bandwidth.
The ESO is the ADRC's major key. The precision of any control system is largely determined by the observer's accuracy. Various observer design philosophies have been proposed, including fuzzy observers, sliding mode observers, unknown input observers, perturbation observers, equivalent input observers, extended state observers, and disturbance observers. From these observers, (Han, 2009) proposed the extended state observer (ESO). It calculates the system's internal states, system uncertainties, and exogenous disturbances, as well as designing a state feedback controller. As a result, ESO-based control design has received a lot of attention in recent years (Abdul-Adheem et al., 2020; Zhang et al., 2016). Refer to Fig.3 a (LESO) for a general overview is:
Where
3.2. NADRC
In this type of ADRC, nonlinear functions for TD and PD are used, but the LESO remains the same. It is proposed that a modified tracking differentiator (MTD) be used. (Liu & Jiang, 2017) proposed an equation for improving trajectory tracking performance that is simple to implement and superior to the traditional nonlinear tracking differentiator:
Where, a1 > 0, b1, b2 > 0, n > 0 and n is odd. Here, V1 is the desired trajectory and V2 is its derivative. The value of (r) is determined by the application and is chosen suitably to adapt the transient profile's space. Then, V2 is denoted as the “tracking differentiator” of input signal V(t). In this paper a NLSEF based on Equation (7) given by (Gao, 2006; Shi & Chang, 2011). A non-linear state error feedback function fal(.) is represented by the form:
fal(.) is a continuous power function which has linear segments in the neighborhood of the origin. 𝛿 is threshold of non-smooth interval, α is control parameter. If |e| > 𝛿, fal is linear function used to prevent high-frequency fluctuations caused by high gains in sign function. Otherwise, if |e| > 𝛿, fal is non-smooth function. (0 < α < 1) is an adjustable parameter. NLSEF is formed by the nonlinear combination of state deviations corresponding to NTD and ESO, namely (Alawad et al., 2022):
4. ADRC optimization parameters
There are eight unknown tuning parameters (r, a1, b1, b2, n, α1, α2, 𝛿) as a result of Equations (6) and (7) hence any optimization methods must be used to calculate their values. Grey Wolf Optimizer (GWO) is proposed in this paper (Humaid et al., 2018; Mirjalili et al., 2014). The GWO algorithm is modeled after the natural leadership structure and hunting mechanism of gray wolves. For replicating the leadership structure, four sorts of grey wolves are used: alpha, beta, delta, and omega. Furthermore, to conduct optimization, three primary processes of hunting are implemented: searching for prey, encircling prey, and attacking prey. The ideal design parameters for the ADRC algorithm based on NLADRC are shown in Table 2.
5. Results and analysis
The results of three simulation studies are discussed. Case 1: no effect of disturbance, Case 2: constant load disturbance (5N.m at t=2sec), and Case 3: white noise (noise power=10, sampling time=2sec) were used. The Root-Mean-Square-Error performance index was used for comparison (R.M.S.E) (Nasir et al., 2022).
5.2. No disturbance
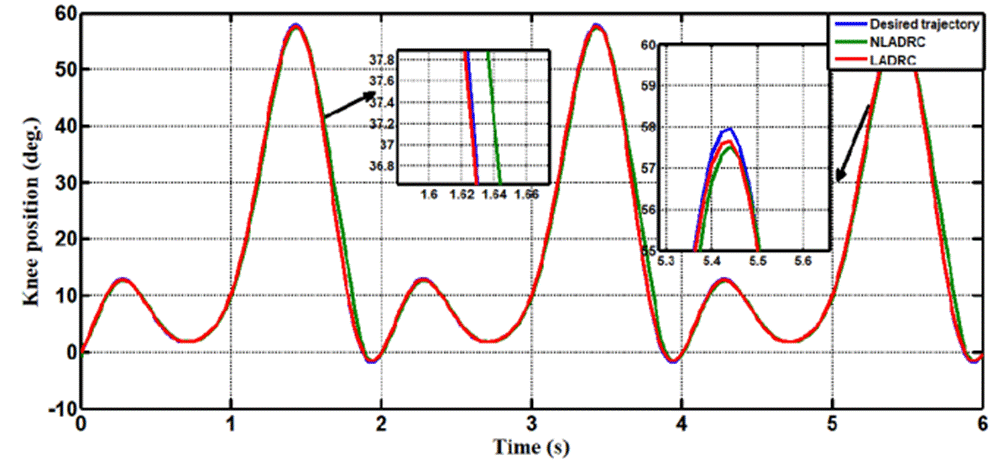
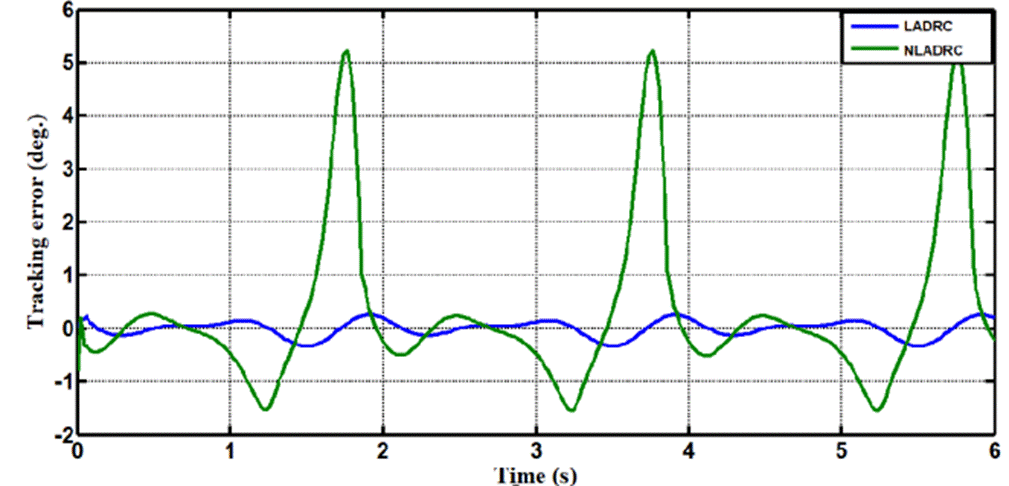
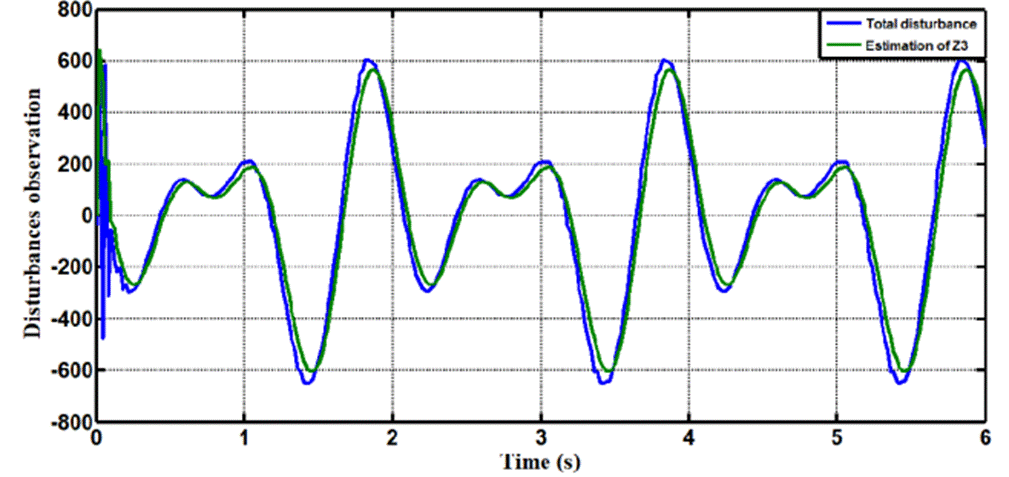
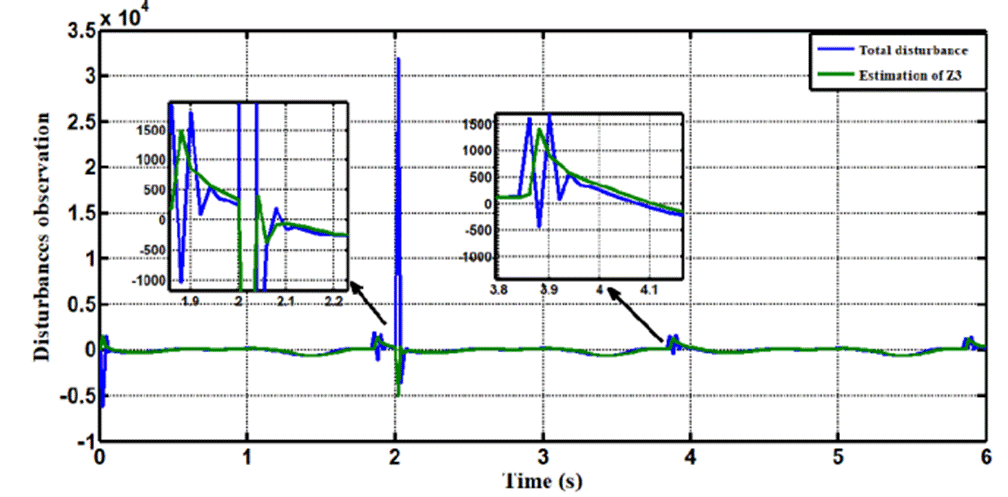
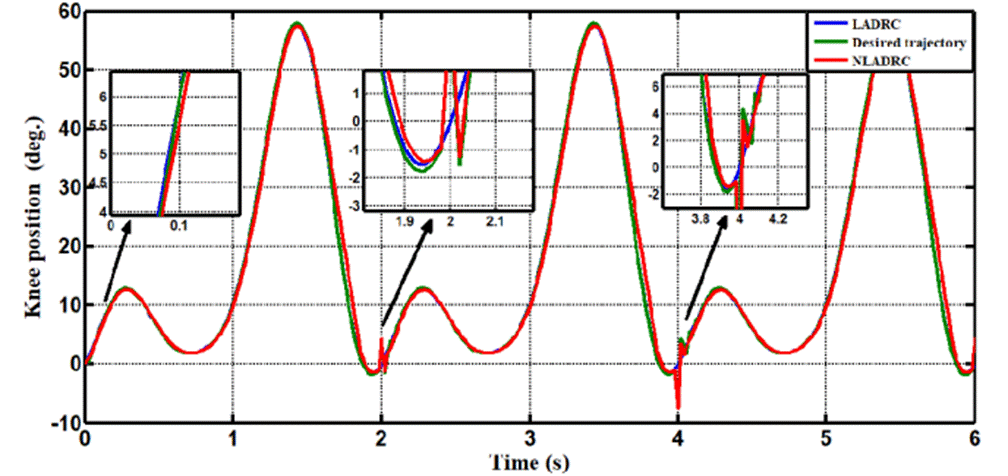
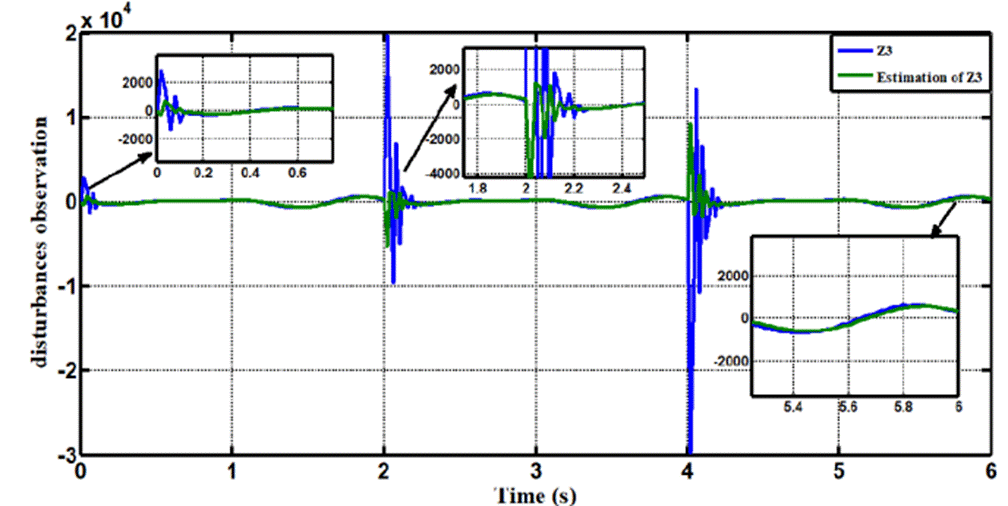
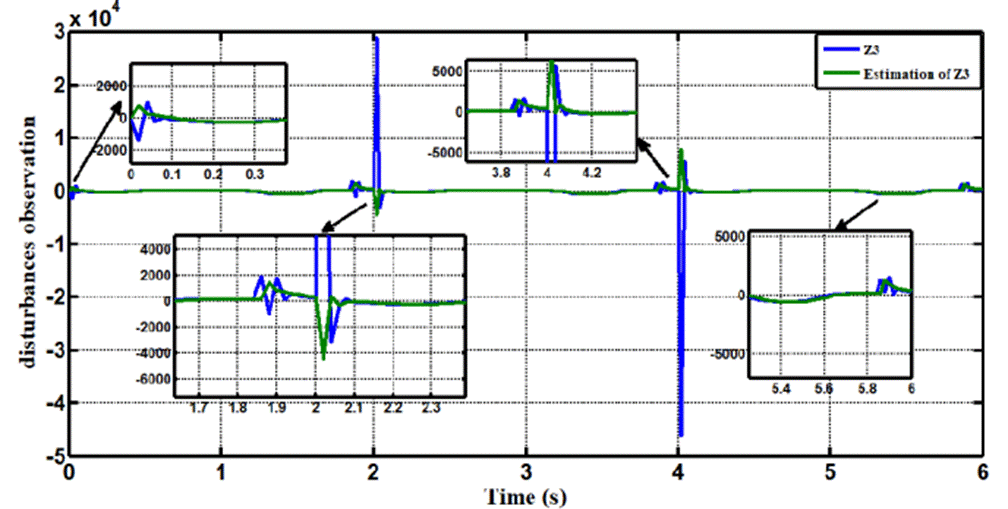
In Case 1, the performance of the ADRC is compared with the proposed controllers (LADRC, NLADRC) without external disturbance. Fig.4 shows the trajectory tracking performance of mentioned controllers for the knee joint, the trajectory tracked by LADRC has best reference tracking, when compared with NADRC. Fig.5 shows trajectory tracking errors for both approaches, the resulting trajectory error of NADRC is more than LADRC. Figures 6 and 7 show the Total disturbance estimation errors for LADRC and NADRC respectively, also it is clear that LADRC gives less estimation total disturbance error and this measure is the key of strong activity of ADRC control in general and specially for LADRC.
5.2. Constant disturbance
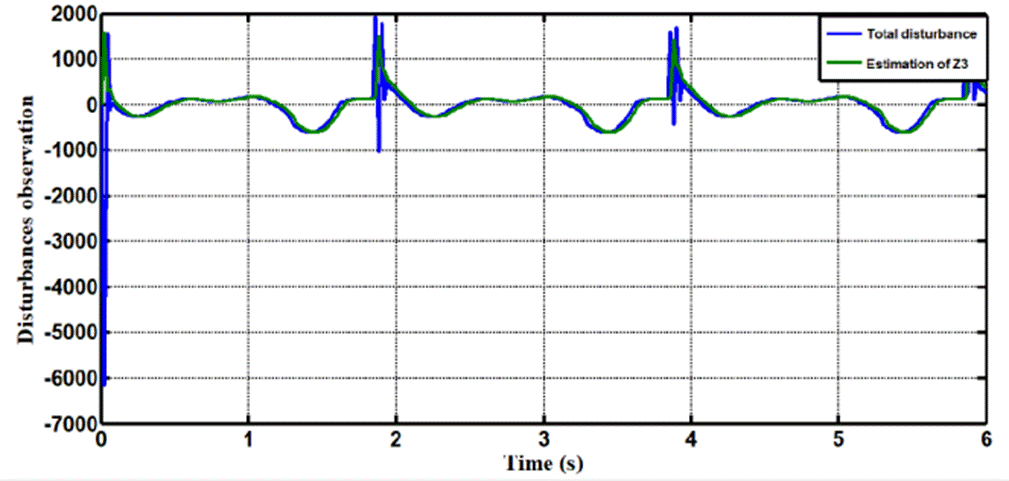
In Case 2, the performance of the ADRC is compared with the proposed controllers with addition of constant load disturbance of amplitude 5 N.m. and t = 2sec at the output during the training. Fig. 8 shows the trajectory tracking performance for various controllers for the knee joints. Fig.9 shows the tracking error for LADRC and NLADRC of the knee joint with constant load disturbance. Figs.10 and 11 show the Total disturbance estimation errors for LADRC and NADRC respectively, also it is clear that LADRC gives less estimation total disturbance error and good trajectory tracking.
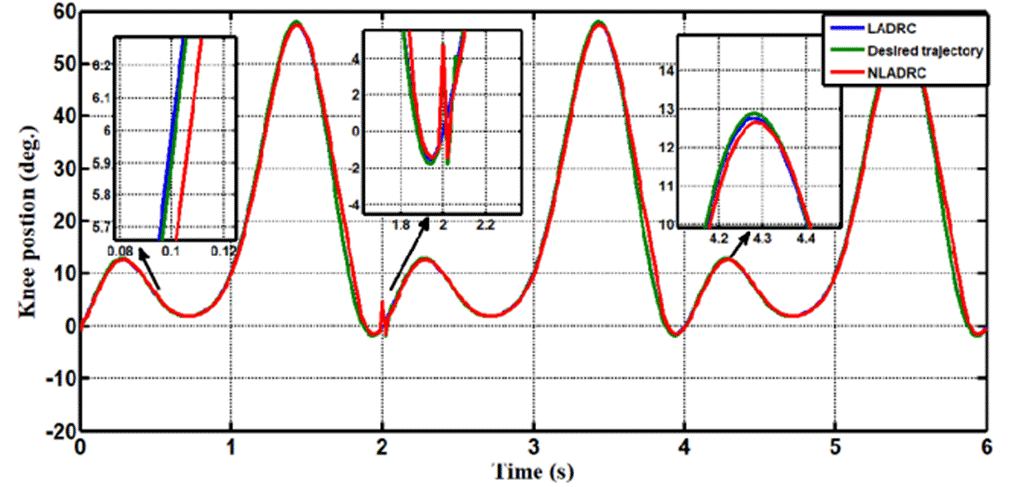
Figure 8 Trajectory tracking comparison of LADRC and NADRC for the knee joint with constant load disturbance.
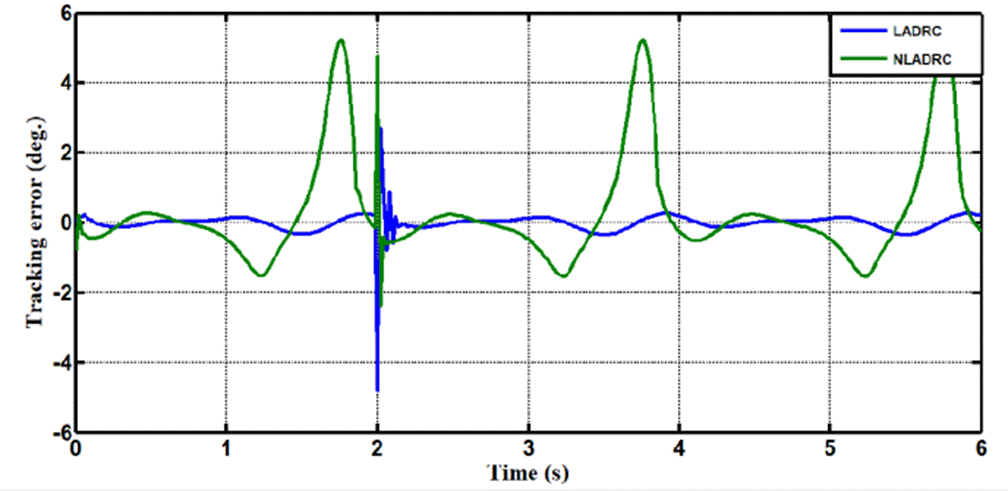
Figure 9 Show trajectory tracking error comparison for LADRC and NLADRC with constant load disturbance.
5.3. Noise disturbance
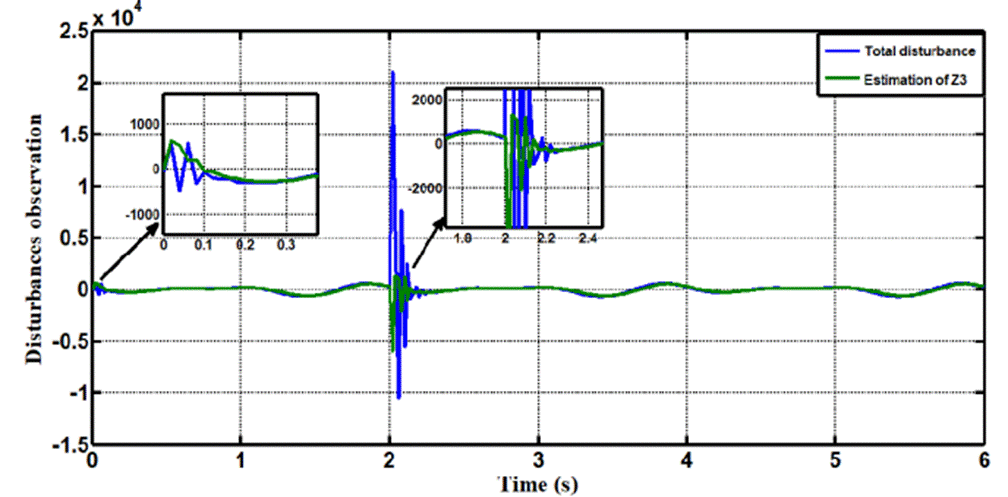
In Case 3, the performance of the ADRC is compared with the proposed controllers with addition of white noise disturbance of power 12 and sampling time=2sec at the output during the training. Fig. 12 shows the trajectory tracking performance for various controllers for the knee joints. Fig. 13 shows the tracking error for LADRC and NLADRC of the knee joint with constant noise disturbance. Figs. 14 and 15 show the Total disturbance estimation errors for LADRC and NADRC respectively, also it is clear that LADRC gives less estimation total disturbance error and good trajectory tracking.
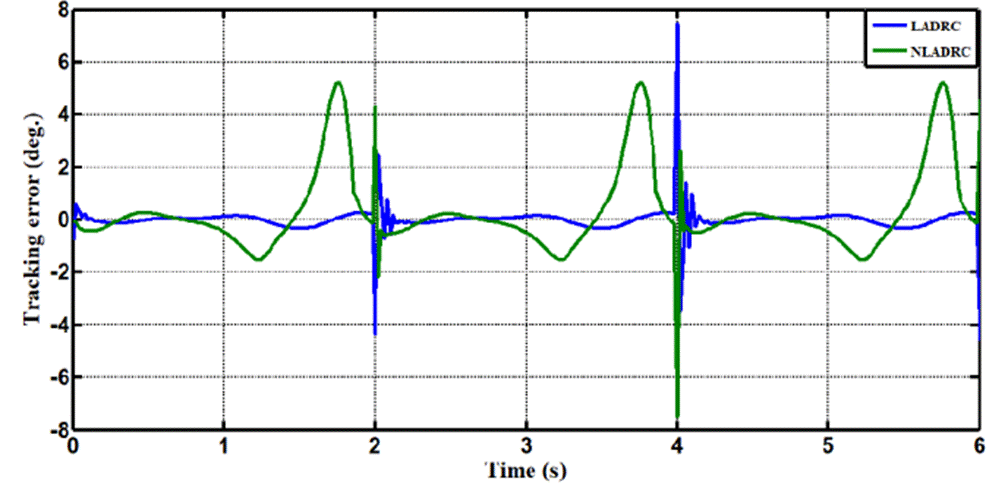
Figure 13 Show trajectory tracking error comparison for LADRC and NLADRC with white noise disturbance.
Again, the results demonstrated the advantage of LADRC approach and the ability to estimate the Knee angle position and the dynamics system much better than NLADRC, this result can be seen mathematically in Table 3, when calculating the performance index (R.M.S.E). As seen, the percentage reduction in (R.M.S.E) of LADRC over NLADRC.
6. Conclusions
This work presents active disturbance rejection control technology and conducts application research on it. Performance comparisons between two configuration (LADRC, NLADRC) aid practicing control engineers in making effective use of this control technology. Based on the simulation results, the following conclusions can be drawn:
1.- This research focuses on creating a control system for gait tracking based on the passive rehabilitative element of a given exoskeleton. The use of exoskeletons for rehabilitation necessitates additional caution because the wearer cannot give joint motion trajectories, and the injured individual is unable to perform the needed tasks.
2.- In the presence of plant external disturbances (constant and harmonics), experimental results show that the resulting controller LADRC provides exact tracking performance in terms of Control effort, output tracking, and disturbance rejection, as well as, more clearly, measurement inaccuracy, are all factors to consider.
3.- It demonstrates that the monitoring of extra state (Z3) is extremely close to total disruption in LADRC, and that ESO of LADRC is very active when compared to ESO of NLADRC in this scenario.
4.- Due to nonlinear terms in NTD, NPD, it needs more tuning parameters and optimization techniques to reach the best values and this increases the problem due to dealing with nonlinear (exoskeleton-human) plant.
5.- Numerically, The LADRC shows a noticeable reduction in index (R.M.S.E), when compared with NLADRC and gives more improvement for training tracking of desired path.











 text new page (beta)
text new page (beta)