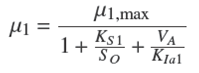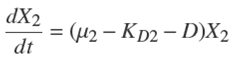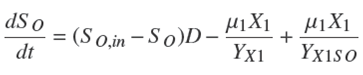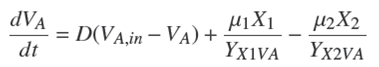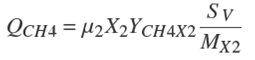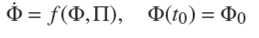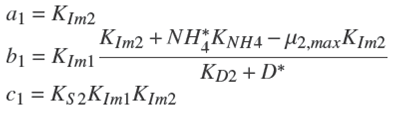1 Introducción

Anaerobic digestion (AD) has recently gained considerable importance as a waste treatment technology to reduce organic matter in agro-food industries and municipal effluents. The AD process presents advantages compared to aerobic treatment as: short hydraulic retention times, low sludge production, high organic load removal, and low initial and operating cost. Recently, much attention has been paid to AD of the organic fraction of municipal solid waste (OFMSW) as an attractive option technology for efficient treatment and simultaneous production of a renewable energy source through the use of biogas (^{Mata-Alvarez et al., 2000}). Nevertheless, its widespread application has been limited, because of the complexity of the process, and difficulties involved in achieving a desirable operation of the AD process. All these aspects can be overcome with the development and improvement of instrumentation and control systems (^{Jimenez et al., 2015}; ^{Méndez- Acosta et al., 2008}). Moreover, with a suitable dynamic model it is possible to evaluate the AD process behavior and to formulate and evaluate control strategies. These models are also used in the modeling, identification, design, optimization, and on-line monitoring of AD process (^{Gómez-Acata et al., 2015}; ^{Cuevas-Ortiz et al., 2015}).

The availability of a simple AD model is desired as it captures the complexity of the process, and allowing the sustained operation under a feedback control law. Because of this, many studies have been devoted to this aim. ^{Kiely et al. (1997}) proposed a nonlinear dynamical model of AD of OFMSW based on three previous models (^{Hill and Barth, 1977}; ^{Moletta et al., 1986}; ^{Havlik et al., 1986}). The model includes: hydrolysis, acidogenic and methanogenic processes, the growth kinetics of acidogenic and methanogenic bacteria; also considered equilibrium between CO ₂ and HCO ⁻, cations and NH ⁺⁴; finally inhibition by ammonia in the growth kinetics of methanogenic bacteria were also considered. ^{Esposito et al. (2008)} described the dynamical anaerobic co- digestion processes of OFMSW and sewage sludge. The model (Esposito et al., 2008) describes the surface based kinetic behavior of the OFMSW disintegration process. From this seminal idea several studies have been reported which include model calibration and validation (^{Esposito et al., 2011a}), effect of the organic loading rate (^{Esposito et al., 2011b}) and enhanced bio-methane production from co-digestion. Other contributions are based on distributed parameters. In this sense, ^{Vavilin et al. (2003}) and ^{Nopharatana et al. (2003)} take into account the change of a set of parameters in the mathematical model involving the flow liquid inside of the digester. Kinetic modeling have been also reported for batch process of AD of MSW (^{Nopharatana et al., 2007}) and semicontinuous OFMSW (^{Fernandez et al., 2010}) under specific operational conditions. ^{Pavan et al. (2000}) reported the kinetic study of a two-phase AD process using diffusional models; in addition, a comparison with a single phase system is also carried out.

A theoretical principle states that the set of operational conditions for AD process allows one to set operational condition and, after that, to propose feedback schemes to control and preserve such operational conditions. Nevertheless, in order to predict how the system responds during or after a change of operational conditions is convenient a mathematical model. The analysis of the dynamical model allows us to formulate changes of operational conditions and control strategies for the AD process (^{Nopharatana et al., 2003}). Although, ^{Alatiqi et al. (1994}) analyzed AD mesophilic and thermophilic processes schemes in terms of stability and controllability, it is not clear yet the role of the inhibition phenomenon. In same direction, ^{Bolzonella et al., (2003}) studied the variations of the process parameters during transient conditions and identified dynamical behavior between changes of stable conditions and parameter behavior; nevertheless, there are not predictions of key variables under an inhibition scenario.

Although several mathematical models reported describe the AD process of organic solid phase (^{Kiely et al., 1997}; ^{Esposito et al., 2008}; ^{Fernandez et al., 2010}), a model is desirable such that operational conditions can be captured and control strategies can be formulated in face to diverse scenarios. Because of operational stability of the AD process is largely dependent on the accumulation of VFA, a model should include the dynamical behavior of VFA inhibitory phenomenon. To our knowledge, only a few contributions, among those that have addressed the VFA accumulation, have identified acidification as open-loop stable operational condition (^{Méndez- Acosta et al., 2008}; ^{Myint et al., 2007}). Moreover, the problem of the operational instability due to the accumulation of VFA remains open. In this study a mathematical modelling of AD process and mathematical analysis is addressed towards control design. The first objective is the design a mathematical model as simple as possible in terms of main key variables. The technical difficulty resides in the capability of the model to captures the dynamics of the main operation conditions of real continuous AD process as washout condition, acidification condition and normal operation condition. The second objective is the design a control scheme that is capable of regulating the VFA concentration in continuous AD process.

This contribution is organized as follows. A reduced dynamical model is proposed and dynamic features are exposed and analyzed in Section 2. In Section 3, a control problem is formulated for a continuous AD of OFMSW process. Then, in Section 4, a PI classical feedback controller is derived and some simulations are shown in order to illustrate the performance of the controller. Finally, some concluding remarks are addressed.

2 Model description

The dynamical model is derived from previous proposals (^{Hill and Barth, 1977}; ^{Moletta et al., 1986}; ^{Kiely et al., 1997}). The model describes the dynamical behavior of AD process of OFMSW through a set of nonlinear ordinary differential equation (ODE). Each ODE is based on mass balance of components of the continuous isothermal AD process. For overall AD for OFMSW includes four steps: hydrolysis, acidogenesis, acetogenesis and methanogenesis. The hydrolysis is recognized as the rate-limiting step for overall AD process, while methanogenesis is the rate-limiting step for easily biodegradable substrates (^{Ariunbaatar et al., 2014}; ^{Fernández-Gu ̈elfo et al., 2011}). The separation of the hydrolytic stage from the methanogenic enhances a stable development of each biochemical reaction, promoting organic matter degradation and biogas production. Pretreatment for the organic solid fraction and OFMSW might be needed in order to ensure the transformation of insoluble organics matter to soluble compounds (^{Ariunbaatar et al., 2014}; ^{Cesaro et al., 2014}). Thus, the hydrolysis stage is neglected in the model but assumed to be performed at previous pretreatment stage.

The relation among microorganisms and substrates is defined by mass balances under isothermal condition. Four substrates are considering: soluble organic mater, volatile fatty acids, ammonia and methane. Acidogenic and methanogenic bacteria are included in the model. The inhibition by volatile fatty acids has been considered into the specific grow rate of acidogenic bacteria. In addition, ammonia and volatile fatty acids inhibition are included into the specific grow rate of methanogenic bacteria. The processes start with the degradation of organic soluble matter. Continuous production of soluble organic matter is supposed by the enzymatic action of the acidogenic bacteria. In the next stage, acidogenic bacteria produces a series of acids. Nevertheless, only acetic acid is considered in the model. Finally, acetoclastic methanogenic bacteria converts acetic acid to methane. The pH is assumed constant and the ionic dilute equilibrium is preserved. The pressure is assumed constant P = P_atm ; which means that despite of the fact that there is a continuous production of mixture of gases (CH ₄, CO ₂, NH ₃) the pressure of the AD process is maintained to P_atm . Then, the produced mixture of gases is assumed to go directly out of the digester. The NH ₃ production rate is supposed less than methane and carbon dioxide rates. During biochemical reactions CO ₂ is also produced. Nevertheless, as operating conditions (pH, temperature and pressure) and ionic equilibrium are preserved, the relation between CH ₄ and CO ₂ is assumed constant. Then, CO ₂ and NH ₃ gas production rate are not modeled. Under above assumptions and conditions, the dynamical behavior for acidogenic biomass is described by (^{Hill and Barth, 1977}; ^{Moletta et al., 1986}):

(1)

where X ₁ is the acidogenic biomass [mg/l]; K_D1 is related to the death rate of acidogenic biomass [d ⁻¹]; D is the dilution rate [d ⁻¹]; and μ ₁ is the specific growth rate of acidogenic biomass [d ⁻¹] defined by (^{Kiely et al., 1997}):

(2)

where μ_1,max stands for the maximum specific growth rates [d ⁻¹]; K_S1 denotes the saturation constant for the acidogenic bacteria growth [mg/l]; K_Ia1 is the inhibition constant of acidogenic bacteria growth [mg/l] which is related to volatile acid inhibition; S O is the soluble organic matter concentration [mg/l]; and VA is the volatile acid concentration [mg/l]. The dilution rate D [d ⁻¹] is defined as the ratio of the inlet flow rate Qin [ld ⁻¹] respect to the reactor volume V [l]. The dynamic description for methanogenic biomass is described by (^{Hill and Barth, 1977}; ^{Moletta et al., 1986}):

(3)

where X ₂ is the methanogenic biomass [mg/l]; K_D2 is related to the death rate of methanogenic biomass [d ⁻¹]; D is the dilution rate [d ⁻¹]; and μ ₂ is the specific growth rate of methanogenic biomass [d ⁻¹] defined by (^{Kiely et al., 1997}):

(4)

where μ _2,max is the maximum specific growth rates [d ⁻¹]; K_S2 is the saturation constant for the methanogenic bacteria growth [mg/l]; K_Im1 is the inhibition constant of methanogenic bacteria growth [mg/l] which is related to volatile acid inhibition; K_Im2 is the inhibition constant of methanogenic bacteria growth [mg/l] which is related to inhibition by ammonia. The mass balance of the first stage is the dynamic of soluble organics S O [mg/l] consists of the following terms: (i) inlet-outlet mass balance related with dilution rate D; (ii) consumption by acidogenic bacteria with a yield coefficient Y_X1 [mg X ₁/mg S_O ]; and (iii) production by acidogenic bacteria with a yield coefficient Y_X1SO [mg X ₁/mg S_O ] (^{Hill and Barth, 1977}).

(5)

The mass balance of the volatile organic acids VA [mg/l] consists of the following terms: (i) inlet- outlet mass balance related to the dilution rate D; (ii) production by acidogenic bacteria with a yield coefficient Y_X1VA [mg X ₁/mg V_A ]; and (iii) consumption by methanogenic bacteria with a yield coefficient Y_X2VA [mg X ₂/mg V_A ] (^{Hill and Barth, 1977}).

(6)

The mass balance of NH4 [mg/l] consists of: (i) inlet- outlet mass balance related to the dilution rate D; and (ii) production by acidogenic bacteria with a yield coefficient Y_NH4 [mg X ₁/mg NH ₄] (^{Kiely et al., 1997}).

(7)

As low pressure operation and diluted system condition is assumed, mass transference of NH ₃ between liquid and gaseous phases is neglected. Then, the term related to gas-liquid mass transference of ammonia is not included in equation (7) (^{Kiely et al., 1997}).

Because of both ionic equilibrium and pH constant value are assumed, a linear relation between NH ₃ and NH ₄ is defined by:

(8)

where NH ₃ is the concentration of ammonia [mg/l]; NH ₄ is the concentration of ammonium [mg/l]; K_NH4 is a constant which consist of the following parameters: Ki_NH4 = 5.3 _* 10⁻¹⁰ @ 35 ◦C the ionization constant; [H+] is the hydrogen ion concentration (pH = −log[H ⁺]); and the mol weight of NH ₃ and NH ₄ stand for M_NH3 and M_NH4 respectively. For the proposes of this work the pH is considered constant (pH = 7.0).

The methane gas flow [(l_CH4 /l_reactor )d ⁻¹] is described by the following algebraical equation (^{Kiely et al., 1997}):

(9)

where Y_CH4X2 is the yield coefficient for methane forming bacteria [mol CH4/mol org]; SV = 25.4[l/mol @ 35 ◦C] is the standard volume; and M_X2 = 111300[mg org/mol org] is the mole weight of organisms (^{Hill and Barth, 1977}). Under temperature and pressure operating conditions there is very low solubility of methane in the liquid phase. Therefore, methane in liquid phase is neglected. Then, the AD model is defined by a set of differential equations:

(10)

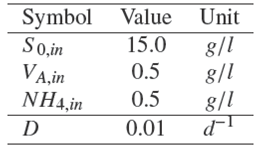
which describes the dynamical behavior of AD process for OFMSW, where the states variables stand forΦ=[X ₁,X ₂,S_O ,V_A ,NH ₄]andanalgebraicrelation of CH ₄ production. The set of parameter π = {μ _1max, μ _2max, K_D1, K_D2, Y_X1, Y_X1SO, Y_X1VA, Y_X2VA, Y_NH4, K_{S 1}, K_{S 2}, K_Ia1, K_Im1, K_Im2, K_NH4 } are real and uncertain constants. The nominal values π₀ ϵ π and additional parameters are shown in Table 1.

Table 1   Specifications for parameters. HB means obtained from ^{Hill and Barth, (1977)}; and K from ^{Kiely et al. (1997)}. Notice that K_NH4 comprises several parameters (see (8)) 

Departing from AD model (10) a complementary analysis is desirable to determine which parameters in π affect the dynamical behavior of the field ƒ (Φ, π). Then, to address the behavior of ƒ (Φ, π) if the parameter values have changed, a sensitivity parametric analysis (^{Khalil, 2002}) has to be done. For a set of parameters π, the approximate solution for the sensitivity function S _ƒ (t) = Φ_π (t, π₀) is computed by the simultaneous solution of the nonlinear nominal AD model (10) and the linear time-varying sensitivity equation (Khalil, 2002):

(11)

where S _ƒ ϵ R ^5×15. The Fig. 1 shows the solution of equation (11) respecting to parameter set π (Table 1), nominal operating condition (Table 2) and initial condition Φ₀ = [1, 1, 1, 1, 1] ^T . The parameters subset having the most significant effect on dynamical behavior of AD model (10) are μ _1max ,μ _2max ,K_D1 , K_D2, K_{S 1}, K_{S 2}, K_Im2 and K_NH4 . The parameters subset is in agree with the results reporter for ^{Kiely et al. (1997)}.

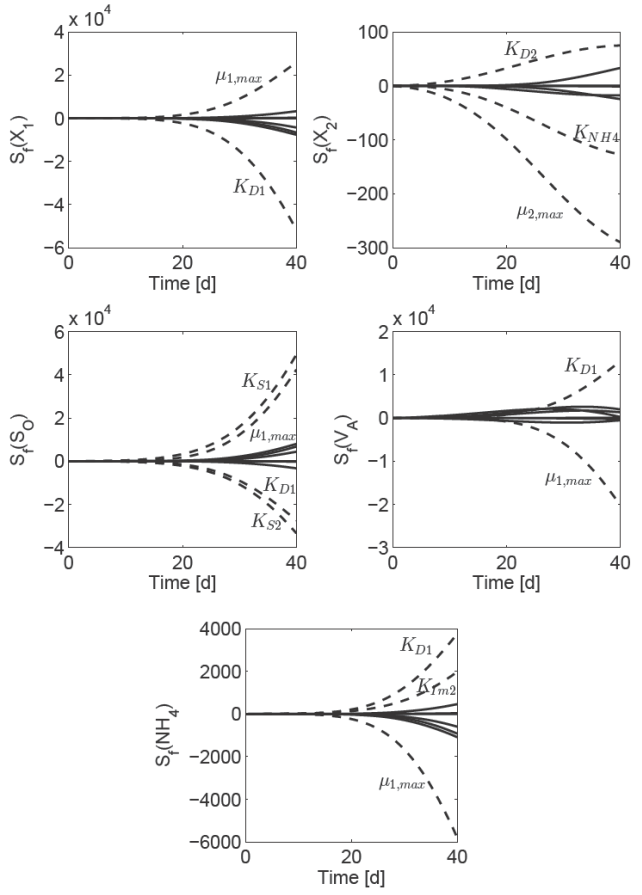
Fig. 1   Numerical solution of the sensitivity function equation (11). Notice that, the parameters subset having the most significant effect on dynamical behavior of AD model (10) are μ_1max, μ_2max, K_D1, K_D2, K_NH4, K_S1, K_S2 and K_Im2 . 

Table 2   Specifications for nominal operating condition. 

3 Open loop dynamical behavior

In order to compare qualitatively the AD model (10) with literature an example of open loop simulations are shown in Fig. 2. The nominal parameters π₀ ϵ π (Table 1) and the nominal operating condition (Table 2) are used for open loop simulation. Two initial condition Φ(t ₀) = Φ₀ were explored. Case one stands for the following initial condition Φ₀ = [0.2, 0.1, 10, 1, 0.5] ^T [g/l]; and case two stands for the initial condition Φ₀ = [0.2, 0.1, 10, 2, 0.5] ^T [g/l]. For case one, the trajectories of the states variables converge at desirable state steady ≠ 0, 0 and < S_O,in , <V_A , _in , <NH_4,in and Q_CH4 >0 for all t >0 (* denotes the equilibrium value). However, for case two the trajectories of the states variables converge at undesirable state steady = 0, > V_A,in and Q_CH4 = 0 for all t ≥ 200 d. Despite of the fact that values of parameters and operation condition are not always valid for a specific composition of OFMSW the qualitative behavior of the states variables are similar to results obtained from literature (^{Hill and Barth, 1977}; ^{Kiely et al., 1997}) in the sense of stabilized and failed condition based on volatile acid concentration and CH ₄ production.

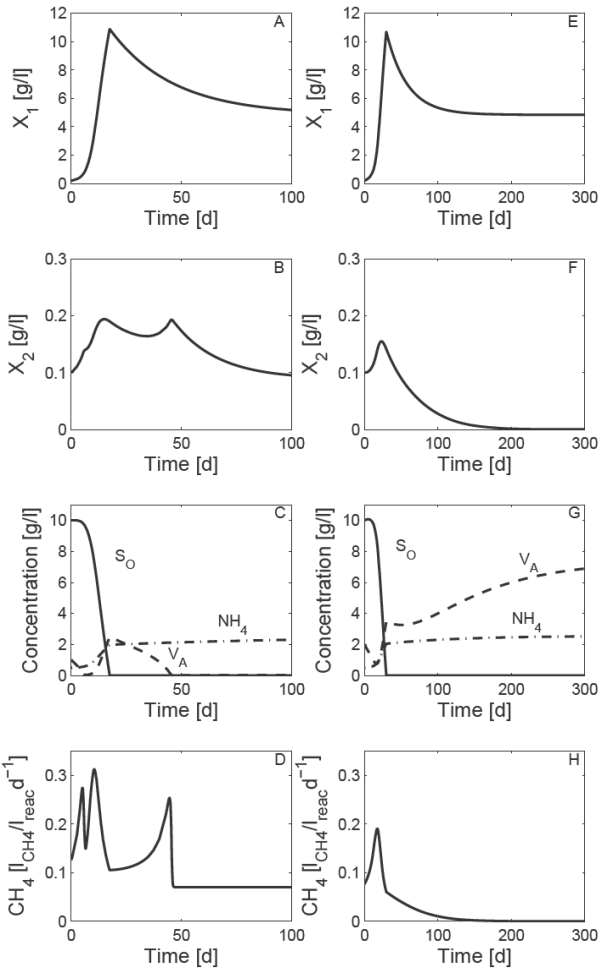
Fig. 2   Numerical solution of the AD model (10) with a set of nominal parameter π₀ ϵ Π (Table 1) and nominal operational condition (Table 2). ABCD) case one stand for initial condition Φ₀ = [0.2, 0.1, 10, 1, 0.5] ^T [g/l]. EFGH) case two stand for initial condition Φ₀ = [0.2, 0.1, 10, 2, 0.5] ^T [g/l]. 

Then, for the same operation condition, it is possible to converge at these two state steady with a set of two different initial conditions. In order to determine convergence to a specific steady state is convenient a dynamical analysis of the equilibrium coordinates. Then, departing from physical properties of the process, equilibrium points stability properties are discussed.

4 The anaerobic digester operating conditions

The following operating conditions can be defined for the anaerobic digester:

5. Dynamic analysis

In order to recognize the possible steady-state solutions for model (10) it is necessary to derive the coordinates of equilibrium. Furthermore, it can be compute equilibrium point and classifier in the sense of stability criterion. Then, such information gives us the main dynamical characteristics of the model. Dynamical analysis of the AD model (10) is performed via linearization principle. Roughly speaking, the procedure consists of the following steps:

First, considering the trivial solution for AD model (10), the coordinate of the equilibrium is:

(12)

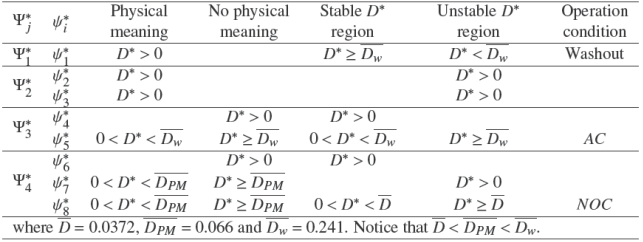
Then, for a nominal values and nominal operation condition, the equilibrium point is ϵ = [0.0, 0.0, 15.0, 5.0, 0.5, 0.0] ^T [g/l] for D* > 0 (Fig. 3). The eigenvalues of the Jacobian matrix of AD model (10) at are shown in Fig. 4. As eigenvalues are positives for D* < 0.241 the AD system is unstable. Nevertheless, the equilibrium point is stable ( < 0) for D* ≥ 0.241. The stable operational condition of is known as washout condition and this undesirable operation arises for D* ≥ 0.241. For practical proposes in real applications this value is known as the upper bound of the admissible dilution rate of operational condition = 0.241.

Fig. 3   Numerical solution of equilibrium point for i = 1 − 8 with a set of nominal parameter π₀ ∈ Π (Table 1) and nominal operational condition (Table 2). 

From AD model (10) under X ₁ = 0 and X ₂ ≠ 0 restrictions, four components of the coordinate of equilibrium are:

(13)

and the coordinate of equilibrium for V_A is determinate for the solution of the following quadratic equation:

(14)

where the coefficient a ₁, b ₁ and c ₁ are:

(15)

As quadratic equation (14) has two solutions and (where > ), two set of equilibrium points are found such as V_A,+ ϵ and V_A,− ϵ . The numerical solution of and are shown in Fig. 3. The eigenvalues and of the Jacobian matrix of AD model (10) at and respectively are shown in Fig. 4. As some elements of and are positive for all D* > 0, the equilibrium point and are unstables, thus these equilibrium points are not arise for D* > 0. It is important to mention that for these coordinate of equilibrium X ₁ = 0, S_O = S_O, in and NH ₄ = NH ₄, _in for t > 0. In other words, this means that the V_A compounds within the wastewater are partially removed by mehtanogenic bacteria (X ₂). Indeed, such operation conditions does not arise in real-life experiments for one stage AD process.

Fig. 4   Numerical solution of eigenvalue of the Jacobian matrix of AD model (10) at for i = 1 − 8 with a set of nominal parameter π₀ ∈ Π (Table 1) and nominal operational condition (Table 2). 

From AD model (10) under X ₂ = 0 and X ₁ ≠ 0 restrictions, four components of the coordinate of equilibrium are:

(16)

and the coordinate of equilibrium for S_O is determined for the solution of the following cubic equation:

(17)

where the coefficient a ₂, b ₂ and c ₂ are:

(18)

As quadratic equation (17) have two solution and (where > ), two set of equilibrium points are found such as ϵ and ϵ . The numerical solution of and are shown in Fig. 3. Eigenvalues and of the Jacobian matrix of AD model (10) at and respectively are shown in Fig. 4. Notice that negative values < 0 for D* > 0 has non physical meaning, then equilibrium point does not arise in real application of AD model (10). The equilibrium point which has physical meaning ⁵⁺) arises for 0 < D* < 0.241. Moreover, as all eigenvalues are negatives ( < 0) for 0 < D* < 0.241 the equilibrium point is stable for 0 < D* < 0.241. Notice that D* ≥ 0.241 is the washout condition at equilibrium point . Thus the stable region of is achieve for 0 < D*< . In order to estudy the physical interpretation of for 0 < D* < considered the accumulation of VFA ( > V_A,in for 0 < D* < , = 0 and ≠ 0). This phenomenon results from the imbalance between acidogenesis and methanogenesis leading thus to acidificatio. Since the methanogenesis is slower than acidogenesis and the espression µ ₂ include inhibition for V_A, the equilibrium point for 0 < D* < is in practice the undesirable acidification condition.

From AD model (10) under X₁ ≠ 0 and x₂ ≠ 0 restrictions, four components of the coordinate of equilibrium are:

(19)

and the solution of the following cubic equation:

(20)

where E_ij (see Appendix A) contain parameters π₀ ϵ π and nominal operating condition. As cubic equation (20) have three solution , and (where ≥ ), three set of equilibrium points are found , where V_A,a ϵ , V_A,b ϵ and V_A,c ϵ . Fig 3 shows the numerical solution of , and . The eigenvalues , and of the of the Jacobian matrix of AD model (10) at , and respectively are shown in Fig. 4. The equilibrium point has non physical meaning ( < 0, ) for > 0, thus does not arise in real application of AD model (10). The equilibrium point has physical meaning; nevertheless, as some eigenvalues are positives for > 0 the equilibrium point is unstable, thus does not arise in real application of AD model (10). The equilibrium point has physical meaning for D < D_PM where D_PM = 0.0372, nevertheless eigenvalues are negatives only for 8 0 < < 0.0372. Then is a stable equilibrium point for 0 < < 0.0372. Indeed, is a desirable operating condition for real application of AD model (10) known as normal operation condition ( > 0, > 0, < S₀,_in, and < for 0 < < 0.0372). Then for AD model (10), exists a lower and upper operating bound [ , Ḏ ] such that ϵ = { ϵ | ≤ ₈ ≤ _8max ; > 0 and _8max < ∞} ⊂ where is obtained when Ḏ is used and is _R8max is obtained when is used. Indeed, Ḏ is called the minimum permissible value which corresponds to the minimum dilution rate to guarantee some waste is treated and is the maximum permissible value to ensure stability operation. Then for AD model (10) with nominal parameters and nominal operational condition = 0.0372.

Table 3 shows the numerical evaluation of the equilibrium points for = 1 − 8 for a set of nominal parameter π₀ ϵ Π and nominal operational condition. Notice that case one and case two of open loop simulation (Fig. 2) correspond to steady state of equilibrium points and respectively.

Table 3 Equilibrium point values for i =1−8 of AD model (10) under nominal parameter π₀∈Π and nominal operating condition. Notice that equilibrium points and correspond to steady state of case one and case two of open loop simulation respectively (see Fig. 2). 

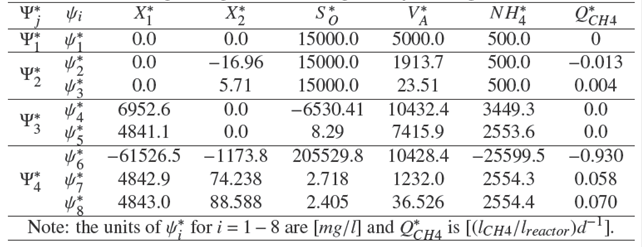
Table 4 depicts the summary of the numerical evaluation of stability analysis. Notice that only the equilibrium points , and exhibit a stable region for such that the equilibrium point has physical meaning. Then, without loss of generality the AD model (10) with a set of nominal parameter π₀ ϵ Π and nominal operational condition admits the following stable equilibrium points:

• Washout condition. It is said that a digester is operating in washout condition as the biomass isinactive(X ₁,X ₂ =0 for all t ≥ 0)and the remaining states are given by its inlet composition (S_O = S_O,in, V_A = V_A,in, NH ₄ = NH_4,in for all t ≥ 0). This condition arises for ≥ D_w . Then, to avoid it, the dilution rate is constrained in practice. The washout condition is locally asymptotically stable for D* < and it becomes globally asymptotically stable for D* ( .

• Acidification condition. It is said that a digester is operating in acidification condition as the only methanogenic biomass is inactive (X ₁ > 0, X ₂ = 0 for all t ≥ 0), accumulation of VFA is maintained (V_A > V_A,in ) and some amount of organic matter is treated (S_O < S_O,in, NH ₄ < NH_4,in ) for all t ≥ 0. This condition arises for 0 < D* < . Then, the dilution rate is constrained to avoid it in practice under overload scenario of organic matter. The acidification condition is locally asymptotically stable for 0 < D* < and it becomes globally asymptotically stable for < D* < .

• Normal operation condition. It is said that a digester is operating in normal operation condition as the biomass is active (X ₁, X ₂ > 0 for all t ≥ 0) and the remaining states accomplish S_O < S_O,in , and V_A < V_A,in . Then, a fraction of organic matter feeding to AD process is reduced by the acidogenic and methanogenic biomass activity. The Normal operation condition (NOC) = { ϵ | ≤ ≤ ; > 0 and < ∞} ⊂ is locally asymptotically stable for [ Ḏ, ].

Table 4 Summarize of numerical evaluation of stability analysis. AC means acidification condition and NOC means normal operation condition. 

From the results obtained analytically of coordinates of equilibrium ( j = 1 − 4) and numerical evaluation of and for = 1,2,...,8 under nominal parameter π₀ ϵΠ and nominal operational condition the following conjecture is assessed:

Conjecture 1. Consider the anaerobic digester model = f (Φ, Π). Then, assuming that the inlet composition S_O,in, V_A,in and NH_4,in is piecewise constant, system = f (Φ, Π) has a locally asymptotically stable equilibrium for a constant D* ϵ [Ḏ, ] under normal operating condition (X ₁ > 0, X ₂ > 0, S_O < S_O,in, V_A < V_A,in ). In addition, such an equilibrium point is contained into the close set Ω _NOC = { ϵ | ≤ ; > 0 and < ∞} ⊂ which contains all normal operating conditions; where is obtained for Ḏ* and for respectively.

It is clear that the AD model (10) has two locally stable equilibrium point under [Ḏ, ] operation. Despite of dilution rate restriction [ D , 𝐷 ] the systems can rich two stable states: the desirable NOC or undesirable acidification. If a set of parameters and operating condition remain constant, to rich one of these stable states will depend on initial condition (Φ(t₀) = Φ₀). For real-life application, this assumption is considered valid for lab-scale under controlled condition, where dilution rate is maintained in a constant value and inlet composition is fixed and known. Then, AD model is candidate for application on startup lab-scale AD process under constant operation condition. Another possible application is prediction of small changes of operational condition, where variation in parameters is neglected. In other words, AD model are able to predict NOC, acidification or washout operation condition under initial condition if operation condition (inlet composition and dilution rate) and parameters are remained constant.

For real-life industrial scale application, the inlet composition is not fixed and it varies in time around a nominal value. Such variation can lead in overload organic matter and possible acidification or failure of AD process (washout). Then, in order to maintain NOC and avoid undesirable operation condition it is necessary a control scheme such that NOC is preserved.

6 Feedback control design

When AD process of OFMSW is used for treatment purposes, the control objective is the regulation of the effluent organic matter despite of fluctuations at the inlet composition (i.e. S _O,in , V _A,in ). The overall objective in AD process is the conversion of organic matter into a mixture mainly composes of methane and carbon dioxide. Then, in case of non particulate substrate or non-excessively complex organic matter, the limiting step is the conversion of volatile fatty acids into methane (^{Ariunbaatar et al., 2014}; ^{Fernández-Guëlfo et al., 2011}). In fact, VFA may accumulate provoking the undesirable acidification operation point and the overall failure of the operation. In this sense, the control problem is formulated to achieve a desirable value of V _A through the action of a control scheme.

From AD model (10), it has been shown (Conjecture 1) that = f (Φ, Π) has a locally stable equilibrium point for NOC. Then, by selecting an adequate D* it is possible obtain a desirable value such that ϵ . This objective is accomplished by manipulating the dilution rate D, obeying a control law. In order to design a control law the following assumptions (which are congruent with the previous discussion) are supposed:

(21)

where the bounds Ḏ and are known, D ϵ R₊ and D _sat = sat(D).

Assumption 1 is not restrictive in sense that there is available technology to measure on-line VA by direct relationship with volatile fatty acid (VFA) or indirectly, throughout linear function with another key variable as total alkalinity. Notice that under Assumption 1-3 the controller must be restricted. For practical D is common restricted to avoid washout condition; nevertheless for AD model (10) = f(Φ,Π) as < the saturation function sat(D) is restricted to upper bound to prevent acidification point.

In order to show the control problem is solvable a PI controller is designed. First, a linear nominal plant is derive (^{Khalil, 2002}) from nonlinear AD model (10) at equilibrium point and nominal parameter values π₀ ϵ Π:

(22)

where u is the input variable D and the output variable y is V _A . Then, with the dynamical characteristics of the nominal plant a controller is obtained:

(23)

where K _p,0 is the proportional constant and K _i,0 is the integral constant. Here, since nominal process model (22) is available, a classical tuning method is used in order to obtain the values of K₀ = [K _p,0 ,K _i,0 ]. Using Ziegler-Nichols (Yu, 2002) tuning rule a set of constants are obtained K₀ = [K _p,0 ,K _i,0 ] = [0.0087, 0.31102].

The Fig. 6 shows the numerical results of the performance of the PI controller K0 under set point changes and load disturbances (see Fig. 5) on the nonlinear AD model (10). The load disturbances are simulated with changes in S _O,in among the nominal inlet concentration S _O,in = 15 [g/l] (Table 2). The PI controller performance remains acceptable throughout the simulations; nevertheless it is deteriorated at the set point changes. As set point changes the control input (dilution rate) can lead to undesirable operation condition of the AD process such a saturation, which it can not be accepted in practice. In order to show the performance of the controller under changes of tuning rules, a change in proportional parameter is explored under two additional controllers K1 = [0.75K _p,0 , K _i,0 ] and K₂ = [2K _p,0 , K _i,0 ].

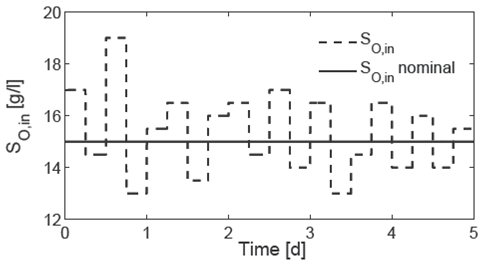
Fig. 5 Inlet concentration disturbances S _O,in for closed-loop simulation of the controlled system. The inlet concentration S _O,in is fixed among the nominal inlet concentration S _O,in = 15 [g/l] (Table 2). 

Fig. 6   Closed-loop behavior of the controlled system under inlet disturbances (see Fig. 5). A) output V _A concentration is maintained close of changes in set point concentration among the coordinate of equilibrium point ∈ = 36.5. B) control input dilution rate D compute by the controller K₀, K₁ and K₂. C) estimate methane gas production rate CH₄ in the controlled system. Notice that controller K₂ achieves the set point values (VA reference) faster with less control effort (D) than controller K₀ and K₁. 

The Fig. 6 shows the numerical results of the performance of the PI controller K₁ and K₂ under inlet disturbances (see Fig. 5). Controller K₀ shows less convergence and major control effort with respect to controller K₁ and K₂. The controller K₂ shows less control effort and faster convergence to V _A,ref with respect to controller K₀ and K₁. Despite of improvement with a trial an error tuning schema, robust control strategies should be explorer.

7 Concluding remarks

A simple model of AD process of OFMSW is proposed for control process. The model includes adequate description of: (i) two metabolic stages such as acidogenesis and methanogenesis are considered; (ii) inhibition product is included; (iii) ionic equilibrium is assumed.

The AD model (10) predicts washout, acidification, and normal operation condition. These operation conditions were addressed for existence and stability criterion. Note that AD model predict acidification condition, it is important issue such that it can be used to obtain confidence intervals of operation, process design and experimental strategies with less disruption.

Under dynamical analysis, it was possible to asses a general framework to synthesize a classical PI controller. Numerical simulations showed that under nominal parameter is possible achieve stabilization of no linear AD process of OFMSW under inlet disturbances. For some change of set point and persistent disturbances the controller present performance organic matter degradation, for these cases is necessary a different framework in order to face this issue; indeed, results in this direction will be reported elsewhere.