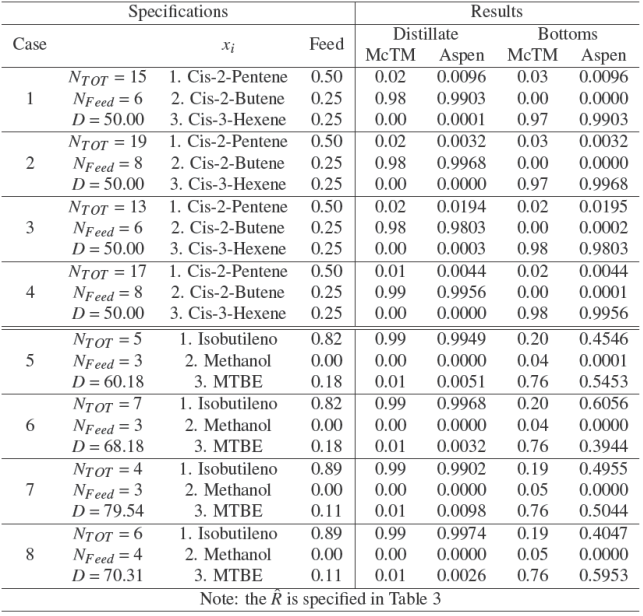
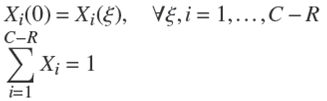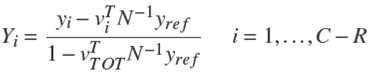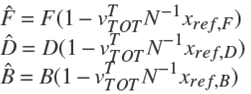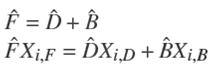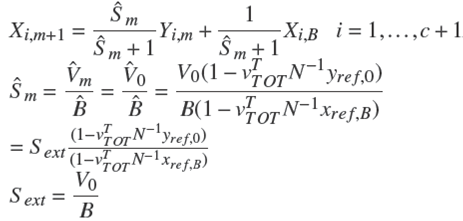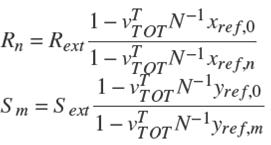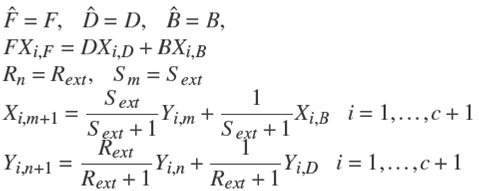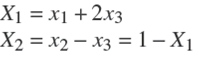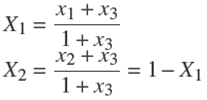1 Introduction
Reactive distillation process integrates functionality of reaction and distillation in combined unit instead of conventional unit process that has single functionality. Combining chemical reaction with vapor-liquid equilibrium provides advantage in the sense of chemical reactions modify the phase behavior. Because of these interactions the modeling and design of reactive distillation (RD) is complex (Segovia- Hernández et al. 2015).
Roughly speaking, the design methods for RD can be classified in three main areas: graphical/topological, optimization-based and heuristics-based. Graphical/topological methods are suitable for feasibility studies but in some cases inefficient for a detailed column design. Heuristics- based methods are useful for post-design analysis. Optimization-based techniques are mathematical- based, involve both physical constraints and appear to be the most flexible and rigorous approach to identify the optimal RD column configurations (Domingues et al. 2014). The solution of these complex models is computationally demanding. Despite of today robust simulation computer equipment and robust optimization-based techniques are available, several optimal design methods can not guarantee the global optimality (Segovia-Hernández et al. 2015). Often, convergence to local optima can only be achieved if good initial guess is available (Avami et al. 2012). Then, as an alternative graphical/geometric methods are used in the initial stages of solution (Carrera-Rodríguez et al. 2014). Indeed, despite of conventional distillation process is considered a mature technology, conceptual approach are still developed (Mendoza and Riascos 2015).
Models and design tools for RD were developed during the last decade (Barbosa and Doherty 1987, Barbosa and Doherty 1988, Espinosa et al. 1995, Bessling et al. 1997, Okasinski and Doherty 1998). Indeed, several short cut graphical methods has been proposed for reactive distillation processes towards preliminary design and visualization of mass balance in reactive column (Carrera et al. 2011). Nevertheless the implementation still remain in solving a set of differential equations or in-out tray by tray calculus. Graphical McCabe-Thiele method was an important tool in the preliminary design of column distillation of nonreactive systems. Several contributions of reactive McCabe-Thiele method have been reported for reactive systems. Similar a binary distillation column, in reactive distillation column three important key variables must be calculate: operation minimum reflux ratio, the number of theoretical reactive stages and feed stage. Espinosa et al. (1995) reported a Ponchon-Savarit using a set of transformed variables proposed by Barbosa and Doherty (1988) including limiting behavior as minimum reflux ratio and minimum reactive stages. Reactive McCabe- Thiele was reported by Lee et al. (2000a, 2000b) for binary mixture assuming reaction equilibrium (isomerization and decomposition) and limiting behavior analysis as total reflux. Conceptual design was developed by Sundmacher and Qi (2003) in a McCabe-Thiele method for limiting behavior, simple reversible reaction in ideal binary mixture and several configuration (i.e. external recycle loop, pre-reactor with nonreactive column on top of a reactive reboiler). A reactive McCabe-Thiele method was developed by Sánchez-Dazaetal. (2003) based on the element mass-balance concept assuming reaction equilibrium on every stage. Graphical design methodology was developed for nonhybrid (Groemping et al. 2004) and extended for hybrid reactive columns for systems with two degrees of freedom (according to Gibbs phase rule) under the concept of reactive stage composition lines (Dragomir and Jobson 2005a, 2005b). Dragomir and Jobson generated multiple designs avoiding in- out tray by tray calculations assuming constant molar overflow.
Based on Dragomir and Jobson's method (2005a), another graphical reactive McCabe-Thiele design methodology has been proposed including thermodynamical rigorous reactive vapor liquid equilibrium calculation (Flores-Estrella 2007). Although graphical reactive McCabe-Thiele design are available, alternative reliable graphical design method including deviations of equilibrium vapor- liquid in tray calculations are still needed. Indeed, it has not been applied to the study of reactive mixtures. The present work introduces a design method for RD column, this approach is similar in concept to nonreactive distillation design method. The present contribution derive some analytical short cut graphical reactive McCabe-Thiele method using transformed composition (Ung and Doherty 1995a) and compare these implications with the analogous binary nonreactive McCabe-Thiele method. A full extension of reactive McCabe-Thiele is restricted to systems with two degrees of freedom (in the sense of Gibbs phase rule systems) and the reaction equilibrium on every stage is assumed. The implication of deviation of equilibrium vapor-liquid is included, we propose a new concept of reactive Murphree efficiency for vapor phase in RD column. To the best of our knowledge, reliable short cut methods for RD are not available yet for deviations of equilibrium vapor-liquid in reactive tray calculations. Finally, the performance of our graphical method is compared with those obtained with the commercial simulator AspenONE Aspen Plus using a rigorous method (Radfrac module) for several reactive systems. Results show the capabilities of this method for the design of RD columns.
2 Description of a reactive McCabe-Thiele method
2.1 Transformed compositions
Ung and Doherty introduced a set of composition variables for treating phase equilibria in multicomponent, multi-reaction systems with or without inert components (Ung and Doherty 1995a). For a system of R independent reactions among c reacting components with I inert components for a total of C = c+I species and II phases; the transformed composition variables are denote by:
where xref
is the column vector of r reference component mole fractions,
The first condition is related with the conservation of mass at each value of the extent of reaction, indeed the transformed variables can be thought of as reaction-invariant compositions. For a Π = 2 (vapor-liquid phases), only C − R − 1 are independent transformed composition variables. This matches the degrees of freedom (C − R − 1) given by Gibbs phase rule for isobaric reactive mixtures (Ung and Doherty 1995b). Therefore, for a isobaric system with C − R = 2 only have one degree of freedom. Then, for a temperature range (similar to nonreactive systems for two components) where reactive vapor- liquid equilibrium exists, it is possible to calculate a two dimensional equilibrium curve in terms of transformed composition variables. Defining the transformed composition in the liquid phase by (1) and vapor phase by:
it is possible obtain (analogous to system without reaction) a continuous isobaric vapor-liquid equilibrium curve in a range of temperature where reactive equilibrium exist. It is important to mention that the range of transformed composition variables value it is not necessary the unity.
2.2 Design equations
According to Barbosa and Doherty's method (1987, 1988) it is possible describe the steady-state operation of reactive distillation columns in terms of transformed compositions. For these equations the following assumption has to be account:
The heat losses from the column walls are negligible.
The molar molar heat of vaporization for the mixture is constant.
The increase in sensible heat with increase in temperature through the column is negligible.
The heat of reaction is negligible compared to the enthalpy of the vapor phase.
The feed is saturated liquid.
Vapor-liquid equilibrium is achieved on each plate.
The column operates with a total condenser.
Under such assumptions, systems without reactions guarantee: (i) a constant molar overflow and (ii) vapor-liquid flow rates in each section of a distillation column are constant. Nevertheless, due to changes in the total number of moles by reaction, only the vapor flow rate is constant in each section of the reactive distillation column and the liquid flow rate in each section of the column only change due to changes in the total number of moles by reaction.
Then, as in the transformed composition, flow rates are defined as (Ung and Doherty 1995c):
According to (1) and (4) the general and component mass balances are defined (Ung and Doherty 1995c):
Assuming m plates for a reactive stripping section and a single feed, the operating line is defining by:
Similarly, assuming n plates in the reactive rectifying section and a single feed, the operating line for the rectifying section is:
Note 1. Under operating condition of total condenser ( x r e f , 0 = x r e f , D ) Ȓn = R e x t .
It is important to mention that Rn and Sm are function of the overall reaction stoichiometry and depends upon the change in the internal flows due to reaction (Dragomir and Jobson 2005a):
Considering isobaric full reactive column for system with C − R = 2 and defining operation conditions similar to a nonreactive distillation column; for a tray by tray calculations the Eq. (6) and (7) are not a unique line because are function of xref,n
and yref,n
as Eq. (8) depicts (even if we consider a sutured liquid feed and a total condenser). In order to extend a full McCabe- Thiele in to reactive system we consider vTOT
= 0 (only for operating lines), then
Note 2. Similar to the classic McCabe-Thiele method; for nonreactive system to
ensure a internal constant
Under the previous assumptions it is possible compare the classic McCabe-Thiele method for nonreactive system (Seader 1998) and a proposed reactive McCabe-Thiele method, even considering limiting behavior (Minimum number of equilibrium stages and Minimum reflux ratio). The Table 1 showed the comparative between these two methods.
As extension of Murphee plat efficiency (Seader 1998) for reactive McCabe-Thiele a vapor efficiency is proposed to describe individual tray performance under transformed composition. Applied to the vapor phase, it can be defined by:
where
The general procedure for design is as follows:
Specify compositions for the feed, top and bottoms products, set ratio of reflux to minimum reflux, feed flow rate and phase condition. For the overall mass balance (to satisfy the number of degrees of freedom) specify D/F or B/F.
Calculate the vapor-liquid equilibrium curve in transformed composition at column operating pressure.
Calculate the minimum number of equilibrium stages and minimum reflux ratio.
Calculate the reflux ratio and the set of slopes for rectifying and stripping section operating lines taking in to account the qˆ-line.
Set reactive stages for rectifying section until the criterion of composition of bottoms be accomplished.
Set reactive stages for stripping section until the criterion of composition of bottoms be accomplished.
For a reactive Murphree efficiency, set reactive stages for rectifying and stripping section from reboiler to total condenser until the criterion of composition of distillate be accomplished.
Despite of our method does not depend of the thermodynamical model, it is important to mention that high nonlinear behavior (i.e. near of pinch point, reactive azeotropes) are not predicted by linear equations (9).
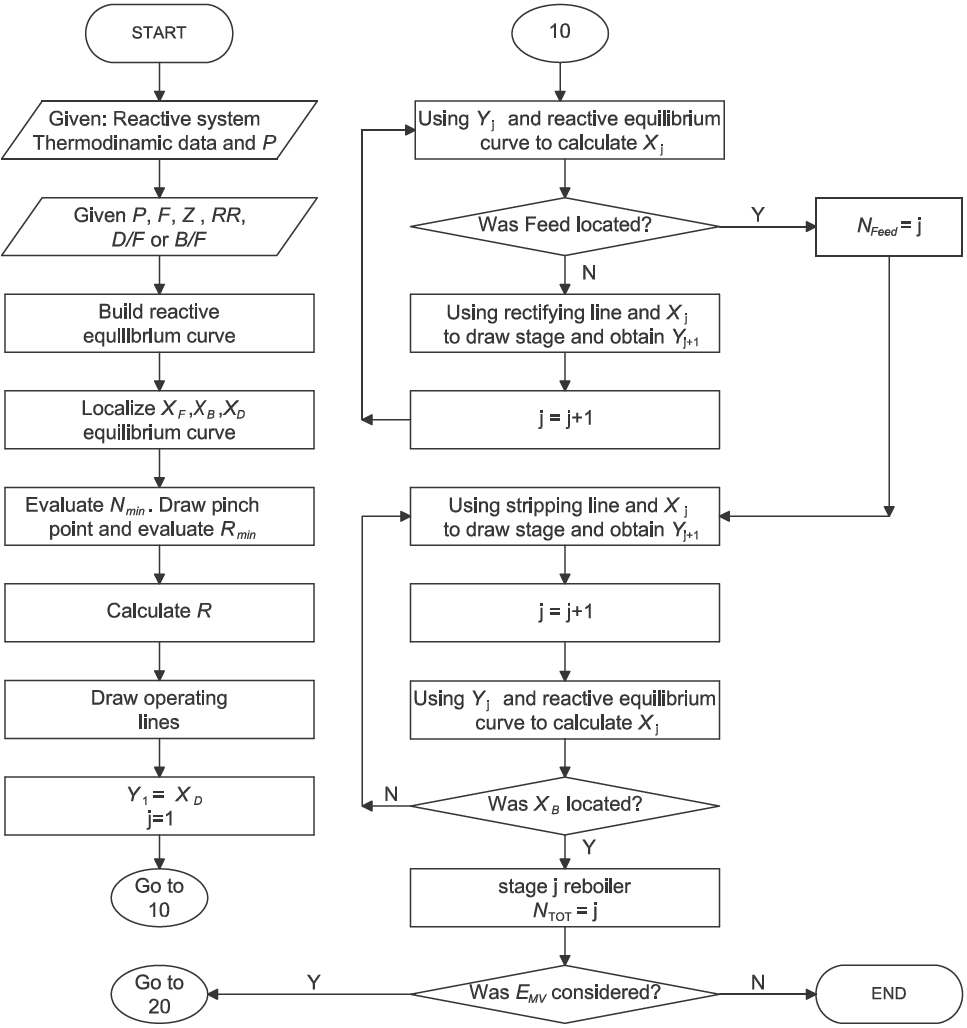
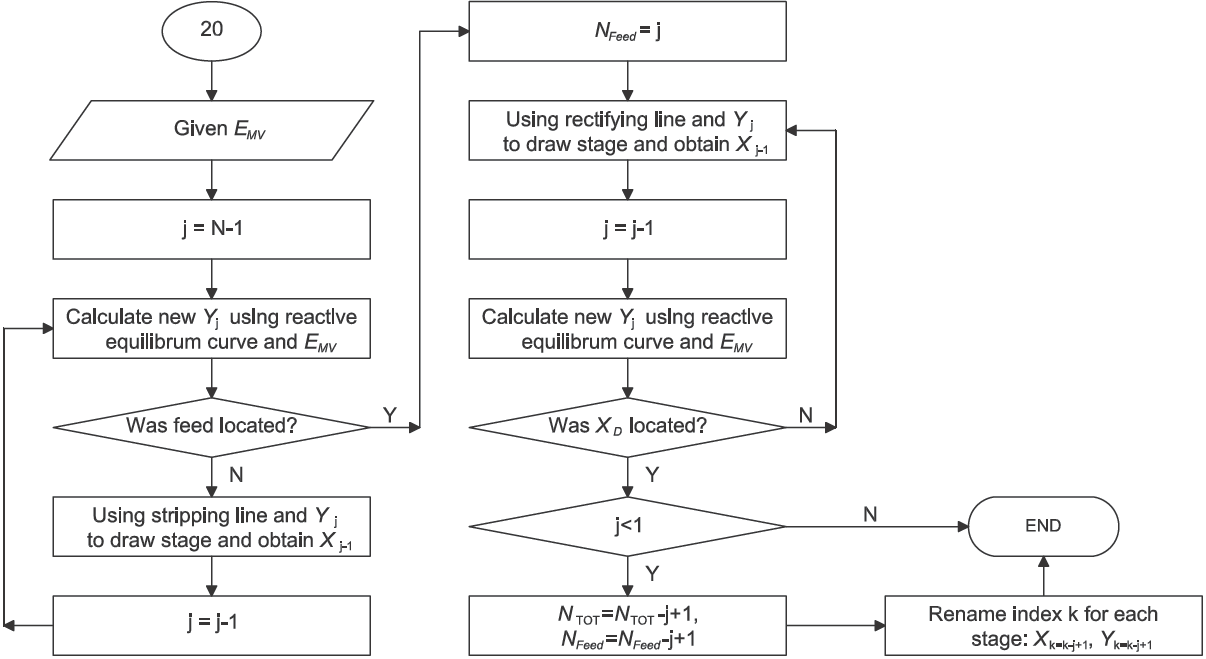
The detailed design procedure is shown in Figure 1 and Figure 2. It is important to point out that stages extends from the top section of the RD column to the bottom. Then, the partial reboiler is equilibrium stage N. Indeed, the number of reactive stages obtained involves a partial reboiler and considers the use of a total condenser. As reactive Murphree efficiency is defined only for tray vapor-liquid efficiency, it is not applied to stage N. It is convenient to remark that the operating minimum reflux is determined until a single calculation related to intersection of operating rectifying line with
3 Results and discussion
Two systems are considered for the proposed graphical design method. The first example is a design of reactive distillation column for the metathesis of 2−pentene (MP) (Okasinski and Doherty 1998). The reversible reaction of 2−pentene (x 1) from 2−butene (x 2) and 3−hexene (x 3) has ideal vapor- liquid equilibrium at atmospheric pressure over the temperature range of [4,65.5]◦C. The reaction equilibrium constant is considered equal Keq,ref = 0.25 [@T = 25◦C] with temperature dependence under the Van't Hoff expression. The transformed composition with 2−pentene as reference component are:
In the second case, we consider the synthesis of Methyl tert-butyl ether (MTBE). The reversible reaction of MTBE (x 3) from isobutene (x 1) and methanol (x 2) without inert was reported by Barbosa and Doherty (1988).
The transformed composition with MTBE as referent component are defined by:
It is important to notice that the method proposed does not depend of the thermodynamical model used for the calculus of reactive vapor-liquid equilibrium. The thermodynamic data for both systems are given in Table 2. An algebraic method that includes transformed compositions and transformed Gibbs energy minimization was used for determine phase compositions in reactive systems (Iglesias et al. 2006). The numerical procedure used equal area principle (Eubank and Hall 1995, Ung and Doherty 1995b) to determine the composition in reactive systems.
Although the proposal method does not include the design of hybrid column (i.e. nonreactive stages), as alternative, a hybrid method can be used. In this sense, some stages can be calculated with the rigorous method and the rest of the reactive stages can be calculated with the short-cut method.
Eighth cases were explored including vapor saturated feed, liquid saturated feed and Murphree efficiency for vapor phase. The graphical design method for binary transformed composition systems have been developed and compared with obtained by a rigorous method in a commercial standard simulator (Radfrac module of AspenONE Aspen Plus simulator). In order to ensure similar condition calculus in commercial simulator, same thermodynamical model and Gibbs minimization for reaction equilibrium calculus were used. In order to compare the results obtained from Murphree vapor efficiency in reactive McCabe-Thiele, a modification of:
Table 3 shows the cases for MP and MTBE system in terms of transformed composition space. For all cases in the reactive McCabe-Thiele is considered a total condenser and partial reboiler; these conditions is also amused in rigorous simulation (RadFrac module). Fig. 3 shows the reactive equilibrium curve of MP and MTBE systems and the graphical solution for limiting behavior. Then, under specification in Table 3: (i) the minimum equilibrium stages at infinity reflux ratio is obtainedand,(ii) theminimumrefluxratio (
Four cases are explored for MP system and the specification design are depicted in Table 3. Fig. 3 shows the reactive equilibrium curve of MP system in transformed composition. Distillate specification of XD,1
= 0.98 indicates rich composition of 2−butene (x
1 = 0.02, x
2 = 0.98) and bottom specification of XB,1
= −0.98 connotes rich composition of 3−hexene (x
1 = 0.02, x
3 = 0.98). The Feed is fixed to XB,1
= 0.0 which corresponds x1 = 0.5, x
2 = x
3 = 0.25 in molar composition. Results in the sense of limiting behavior: (i) the minimum reactive stage
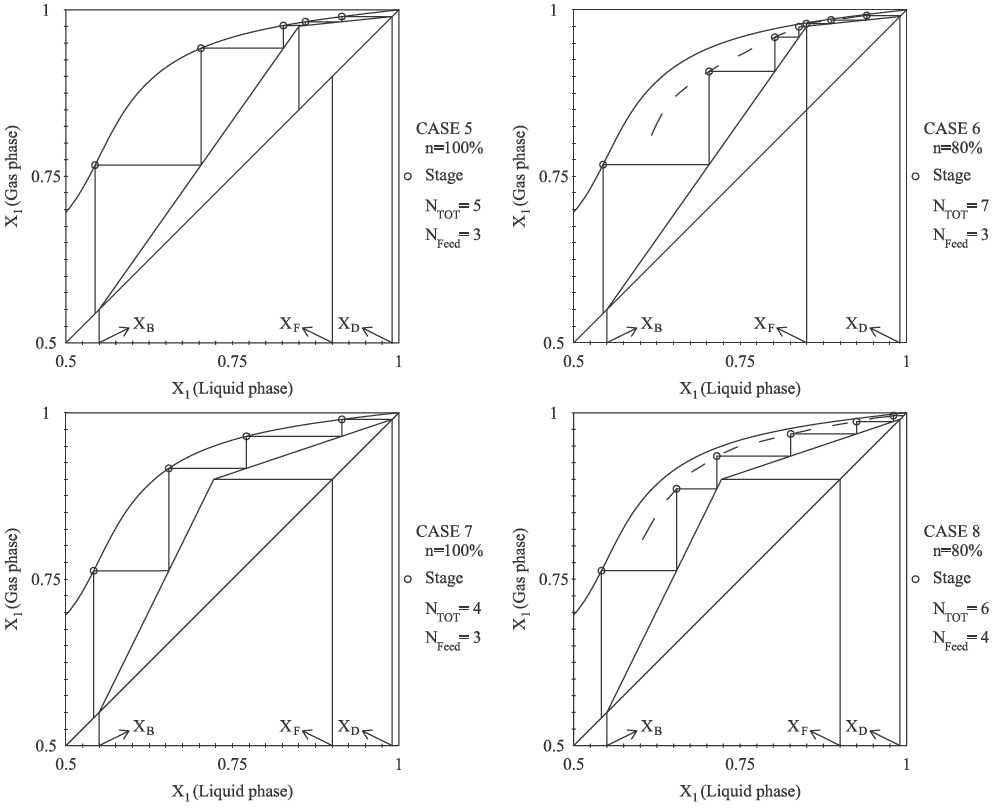
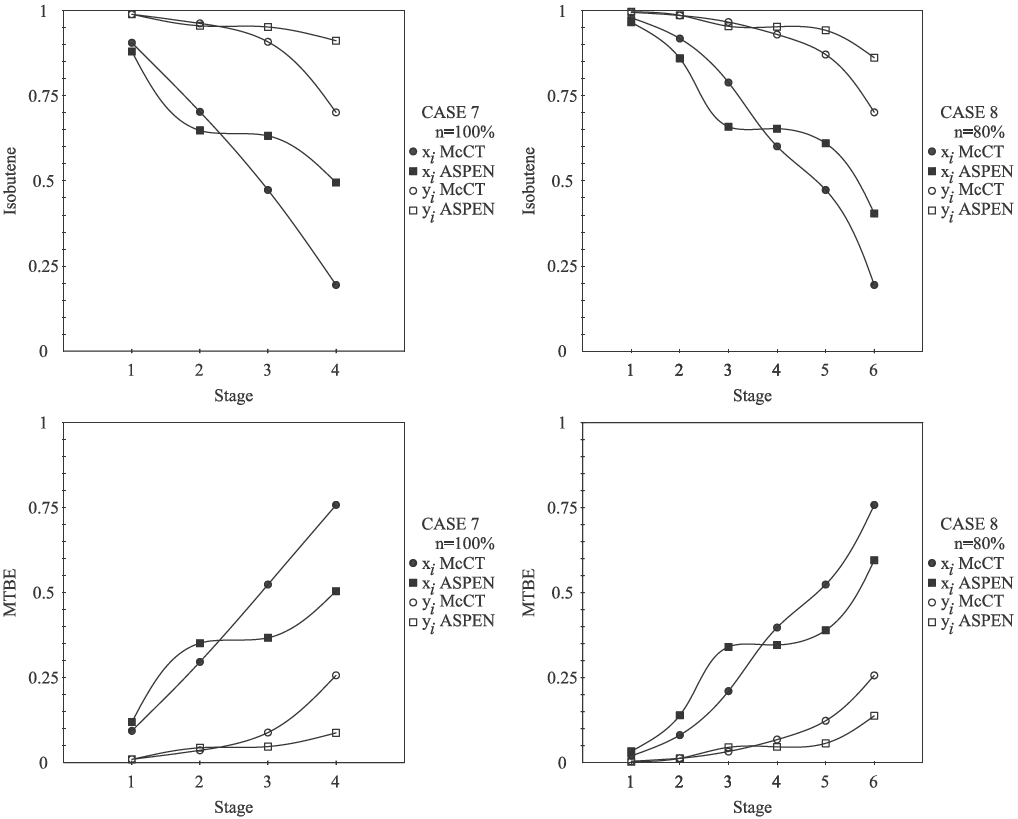
Fig. 5 shows the reactive McCabe-Thiele results for or MTBE system. The highest obtained concentration of MTBE is near of X 1 = 0.5 in the binary reactive equilibrium curve when the concentration objective in bottoms column is fixed at X 1 = 0.55 which corresponds xMT BE = 0.75.
The distillate concentration is rich in isobutene and it is fixed at xiso = 0.99 which corresponds X 1 = 0.99. Case 5 and 6 studies the vapor and liquid saturated feed under 100% tray vapor efficiency, the case 7 and 8 takes the specification of previous cases (5 and 7 respectively) and assume reactive Murphee plat efficiency of 80%. The results for MTBE system are shown in Fig. 5.
With the results obtained in reactive McCabe- Thiele method, the rigorous method was simulated in RadFrac module. In order to homogenize results, the plates are counted from top to bottom and for all designs the total condenser is not considered a reactive stage. Eight cases were compared under specifications depicted in Table 4. Fully feed specification, number of stages, feed stage, reflux ratio, distillation ratio and vapor plat efficiency were specified in RadFrac module. The bottom and distillate product composition for MP system (case 1 − 4) obtained from proposed method are in good agreement with those obtained from commercial simulator using a rigorous method. The approach proposed predict similar results for product composition in distillate for MTBE system (case 5 − 8); nevertheless the approach might be less accurate in predict results for molar fraction composition in bottom product because rigorous simulation (RadFrac module) uses mass and energy balances on tray by tray calculations. Our results show that, it is observed a satisfactory agreement between the short cut method and rigorous simulation, nevertheless the molar profile of MTBE system is in less agreement than MP system. This behavior is attributed to equimolar assumption. Because MTBE reaction present change in number of molecules, the proposal method might be present mayor discrepancies with results obtained by rigorous mass and energy balances. Then, we expect that our methodology are not accurate in high non-equimolar systems.
Temperature profiles results are presented in Fig. 6. Despite of the fact that energy balances are not take into account in reactive McCabe-Thiele method, temperature profiles obtained from equilibrium stages are in good agreement with those obtained from commercial simulator using a rigorous method. The best agreement between the proposed method and AspenONE Aspen Plus is obtained for temperature profiles of MP systems (case 1-4); this agreement might be less for bottoms temperature stage of MTBE systems (case 5-8) because our method assumes constant molar flows, uses only total mass balances and heat effects along the column are not considered. On the other hand, the rigorous method considers change in numbers of moles, mass and energy balances for modeling each stage. Despite of our method is not recommended for rigorous optimization design including heat requirements, it provides a predesing for a rigorous design method, such as operating parameters, concentration and temperature profile as initial iteration.
Many designs are possible under the proposed methodology; to illustrate the implementation, results of vapor saturate for MP system and liquid sutured for MTBE are shown in Fig. 7 and Fig. 8 respectively. Comparative between compositions profiles (component in the vapor and liquid phases) of MP and MTBE system obtained from commercial simulator and that obtained from the proposed design methodology present satisfactory agreement (Fig. 7). Fig. 7 show less agreement between composition bottoms stage of MTBE system (similar to temperature profile of MTBE system in Fig. 6), obtained from commercial simulator and that obtained from the proposed method.
4 Concluding remarks
A new graphical design methodology has been developed for full reactive columns for proposed reactive distillation processes.
The methodology is restricted to systems with two degrees of freedom according to the Gibbs phase rule and single-feed columns. A direct correspondence is made between binary reactive transformed composition and conventional binary nonreactive distillation. Based upon the theory of transformed coordinates, a necessary condition for reactive McCabe-Thiele emerge as similar condition in nonreactive McCabe-Thiele method. The methodology could be extended to more complex configurations, such as double-feed and columns with side-draws.
Application of these methodology is illustrated by considering ideal and nonideal reactive mixtures, became the approach does not depend of the thermodynamic model.
It is assumed that reactive equilibrium vapor-liquid are achieved at each tray and reactive vapor tray efficiency allows us to take into account nonideal behavior in vapor-liquid tray equilibrium. The minimum reflux ratio Rmin and minimum number of reactive stages of this methodology can be easily estimated without iteration. In addition, our method optimizes the feed location by simple inspection similar of nonreactive distillation method.
The present work proposes a reactive Murphree vapor efficiency in order to include deviations in vapor-liquid equilibrium during the calculation of reactive stages. It should be noted that such procedure is performed under transformed compositions variables.
Our extension of the McCabe-Theile method to reactive systems generates estimates of composition and temperature profiles which are in good agreement with those obtained from commercial simulator using a rigorous method.
The results obtained from the proposed method provides an excellent initialization for a rigorous simulation. This graphical method allows us to obtain a pre-design of full reactive column with simple visualization.
Nomenclature
c |
number of reacting components |
C |
total number of components |
° C |
celcius |
H ° |
standard enthalpy of formation |
I |
number of inert components |
N |
square matrix of the stoichiometric coefficients of the reference componentes |
R |
number of independent reactions |
T |
temperature |
|
row vector of stoichiometric coefficients of component i |
|
row vector of the sum of the stoichiometric coefficients for each reaction |
Xi |
transformed composition of component i |
xi |
molar composition of component i |











 text new page (beta)
text new page (beta)