Services on Demand
Journal
Article
Indicators
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista mexicana de ingeniería química
Print version ISSN 1665-2738
Rev. Mex. Ing. Quím vol.10 n.2 Ciudad de México Aug. 2011
Catálisis, cinética y reactores
Evaluación estadística y modelado del comportamiento de un aglomerador de lecho fluidizado
Statistical evaluation and modeling of the behavior of a fluidized bed granulator
D. Ríos–Morales, CO. Castillo–Araiza, R.S. Ruiz–Martínez y M.G. Vizcarra–Mendoza *
Dpto. de Ingeniería de Procesos e Hidráulica, Universidad Autónoma Metropolitana–Iztapalapa. Av. San Rafael Atlixco 186, Col. Vicentina, C.P. 09340, México, D.F. *Autor para la correspondencia. E–mail: mgvm@xanum.uam.mx
Recibido 14 de Junio 2010.
Aceptado 1 de Mayo 2011.
Resumen
En este trabajo se implemento un diseño experimental factorial completamente aleatorizado, con el objeto de evidenciar el efecto de algunos parámetros de operación de un granulador de lecho fluidizado a escala piloto en el crecimiento de partículas sólidas orgánicas. En particular se estudió el efecto del tiempo de alimentación del medio aglomerante (20, 40 y 6 0 min), temperatura del aire (60, 70, 80 y 90° C) y recircular o no los sólidos elutriados a la cámara de fluidización. En la aglomeración de una población de partículas orgánicas con un diámetro promedio inicial de la población igual a 0.121 mm; se atomizó agua destilada como agente ligante y se utilizó aire como medio fluidizante. Un análisis cualitativo de las observaciones en términos del diámetro promedio de la población de partículas aglomeradas, en conjunto con un análisis de varianza (ANOVA) manejando un nivel de significancia del 5%, y el uso de un balance de población discretizado, indicó que la variación del tiempo de aspersión, es el parámetro que tiene el principal efecto en el crecimiento de las partículas, donde los mecanismos de nucleación y agregación son dominantes en el proceso de aglomeración.
Palabras clave: aglomerador de lecho fluidizado, análisis de varianza (ANOVA), diseño factorial completamente aleatorizado, balance de población discretizado (BPD).
Abstract
In the present work a completely randomized factorial experimental design was utilized to identify the effect on particle growth of some op erating variables of a fluidized–bed granulato r at pilot–plant scale. The variables considered were the binder addition time (20, 40 y 60 min), air temperature (60, 70, 80 and 90° C) and whether or not elutriated solids were recirculated back into the fluidization chamber. In the agglomeration process 0.121 mm mean diameter particles of organic nature were used, the bed was fluidized by air and distilled water was sprayed as the binding agent. Based on a qualitative analysis of the average particle size, an analysis of variance (ANOVA) with 5% significance level, and the use of a discretized population balance, it was found that the binder addition time was the main operating parameter acting on particle growth in an agglomeration process where nucleation and aggreg ation mechanisms play a dominant role.
Keywords: fluidized–bed granulator, analysis of variance (ANOVA), randomized factorial experimental design, discretized population balance (DPB).
1 Introducción
En industrias como la farmacéutica, de los alimentos, la agrícola, entre otras, la granulación tiene una aplicación amplia en el procesamiento de partículas ya que permite manipular convenientemente su tamaño y características físicas: fluidez, segregación, dispersabilidad, densidad, fragilidad, mojabilidad, etc. (Nienow y Rowe, 1985; Iveson y col., 2001). En el proceso de granulación una población de partículas sólidas con una distribución de tamaño inicial se humedece por la acción de un líquido aglomerante; las partículas húmedas colisionan entre sí, formando puentes líquidos que al evaporarse dan lugar a enlaces sólidos y, por consiguiente, partículas de mayor tamaño (aglomerado): a esta operación se le conoce como aglomeración húmeda (Nienow y Rowe, 1985). La granulación puede visualizarse como una combinación de mecanismos que tienen lugar durante la aglomeración (Iveson y col, 2001; Lister y Ennis, 2004): humectación, nucleación, consolidación, coalescencia, atrisión y rompimiento.
La aglomeración depende de la naturaleza física del sistema partícula solida–líquido aglomerante, y de las variables asociadas al granulador (Cryer, 1999). El granulador de lecho fluidizado se puede visualizar como un sistema que presenta dos zonas: (1) la zona de aspersión, que es el área donde el líquido aglomerante tiene el primer contacto con las partículas fluidizadas, teniendo lugar el fenómeno de nucleación (Kumar y col. 1997), que depende principalmente del tamaño relativo entre la partícula y la gota formada por el líquido (Waldie, 1991); y (2) la zona de dispersión, que es el área donde se mezclan con aire caliente los núcleos, el líquido aglomerante y las partículas fluidizadas, teniendo los mecanismos de crecimiento, agregación y rompimiento (Ayazi y col. 1990; Tan y col. 2005), que a su vez son función: (a) del tamaño de las partículas; (b) de algunas propiedades físicas del líquido aglomerante: viscosidad y tensión superficial; y (c) de algunos parámetros del proceso: velocidad de aspersión del líquido aglomerante, posición de la boquilla de aspersión del líquido aglomerante con respecto al lecho, velocidad de fluidización, temperatura de entrada y del lecho, humedad relativa, tasa de alimentación del líquido aglomerante, entre otras (Ayazi y col. 1990; Kumar y col. 1997; Schaafsma y col., 2000; Tan y col. 2005). Una de las características inherentes a este sistema de granulación es el fenómeno de elutriación que es el transporte neumático de las partículas de menor tamaño hacía fuera del sistema (Schaafsma y col, 2006).
Si bien diversos granuladores de lecho fluidizado han sido estudiados ampliamente, actualmente no se ha evidenciado satisfactoriamente el efecto e interrelation de los distintos parámetros de operación con el aglomerado de una determinada población de partículas. Cryer y Scherer, (2003) estudiaron el efecto de la velocidad y temperatura de alimentación de aire, carga de sólidos y posición de la boquilla de aspersion, sobre la formación de aglomerados de un producto agroquímico (Flumetsulam). La velocidad y temperatura del aire de alimentación tuvieron un efecto ligero en el proceso de aglomeración, mientras que el efecto de la altura de la boquilla y carga de sólidos fue despreciable. Decanal y Menegalli, (2008) analizaron el efecto de temperatura y velocidad de alimentación del aire, la altura de la boquilla de atomización y presión del aire en ésta, sobre la obtención de aglomerados de polvos de Acerola. La velocidad del aire tuvo un efecto significativo en la formación de aglomerados. La temperatura del aire, altura de la boquilla y presión de aire sobre ésta no presentó ningún efecto en el rango de operación estudiado. Ríos D., (2005) trabajando con un sistema de granulación similar al de Decanal y Menegalli, (2008), encontró que la temperatura tuvo un efecto marginal en la aglomeración de partículas orgánicas, mientras que la variación de la masa sólidos cargada al sistema no presentó efecto alguno. Tan y col., (2006) encontraron que un incremento en la velocidad de alimentación del aire, tiende a reducir la tasa global de crecimiento del aglomerado, mientras que Schaafsma y Kossen, (1999) y Cryer y Scherer, (2003) encontraron resultados opuestos; por otra parte estos grupos de investigación, encontraron un fuerte efecto de la temperatura sobre el crecimiento de las partículas.
Diversos autores han propuesto y/o utilizado diferentes aproximaciones ingenieriles para entender y describir el comportamiento de un proceso de granulación. Un análisis estadístico de un diseño experimental permite determinar cualitativamente el efecto de un parámetro del proceso sobre el aglomerado, tomando como referencia el tamaño promedio de la población de partículas aglomeradas (Montgomery, 2007). Mientras que el uso de un balance de población (BP) (Tan y col., 2005; Soos y col., 2006; Poon y col., 2008), permite tratar de manera fundamental procesos que involucran fenómenos de nacimiento y muerte de partículas en un determinado volumen de control (VC) (Hulbert y col. 1964). Particularmente, para un granulador de lecho fluidizado, el BP se ha utilizado para determinar cuantitativamente la cantidad y distribución del tamaño de partículas en función del tiempo: considerando desde la nucleación hasta su coalescencia y, así, crecimiento y/o rompimiento. Esta clase de modelos considera normalmente expresiones cinéticas para cada uno de los mecanismos de aglomeración involucrados, siendo la elección de éstas el problema central, ya que normalmente son relaciones empíricas que sólo son capaces de describir el sistema en donde se evaluaron, de tal forma que en la actualidad no hay una justificación ni interpretación física aceptable sobre su uso (Cryer, 1999; Hounslow y col, 1988). Por consiguiente, el uso de un BP en la descripción de un granulador de lecho fluidizado ha tenido como objeto entender y determinar el efecto de los distintos parámetros del proceso en los mecanismos de aglomeración (Tan y col, 2005), relacionado la magnitud de las constantes cinéticas correspondientes con las observaciones utilizadas para su determinación (Kumar y col, 1997; Tan y col., 2005; Soos y col., 2006; Poon y col, 2008; Tourbin y col., 2008).
En este estudio es de particular interés analizar el efecto de los parámetros de operación en el comportamiento de un granulador de lecho fluidizado utilizando partículas orgánicas. Si bien es cierto que es muy amplio el número de parámetros que influyen en el comportamiento de esta clase de sistema, tres de ellos revisten especial atención: a) la temperatura del aire de alimentación (To), ya que influye en la consolidación de los puentes líquidos que se establecen entre las partículas (Rhodes, 1998); b) el tiempo de alimentación del líquido aglomerante (ta) ya que es clave para mantener la eficiencia del lecho fluidizado, evitando el fenómeno de defluidización húmeda que se debe al exceso de humedad en la zona de dispersion (Davidson and Harrison, 1985); y c) la recirculación (R) al sistema de los sólidos finos elutriados ya que aparenta tener un efecto en los fenómenos de nucleación (Ríos, 2005). Para esto, se implemento un diseño experimental factorial aleatorizado considerando diferentes niveles en un determinado rango de operación: To (4 niveles: 60, 70,80 y 90oC); ta (3 niveles: 20, 40 y 60 min); R (2 niveles: con recirculación, CR, y sin recirculación, SR). Con las observaciones correspondientes se realizó un análisis estadístico aplicando un análisis de varianza (ANOVA) con un nivel de significancia,, del 5%, lo que permitió, utilizando el software JMP–7, evidenciar cualitativamente el efecto de To, ta y R en el diámetro promedio del aglomerado. Finalmente, se utilizó un balance de población discretizado (BPD) para entender cuantitativamente el efecto de los parámetros de operación en los mecanismo de nucleación, crecimiento y agregación envueltos en el la aglomeración de las partículas estudiadas.
2 Materiales y métodos
2.1 Materiales
Las partículas a aglomerar fueron de tamarindo comercial cuyas propiedades fisicoquímicas se muestran en la Tabla 1. El lote inicial contenía partículas con un tamaño menor a 0.074mm, correspondiente a la malla No. 200, impidiendo tener una fluidización adecuada. Por consiguiente, se acotó la distribución de tamaño inicial manejando partículas de 0.177mm, 0.149mm y 0.105 mm, correspondientes a las mallas No. 80, 100 y 150 respectivamente. Como líquido aglomerante se utilizó agua destilada y como medio de fluidización se utilizó aire.

2.2 Equipo experimental
En la Fig. 1 se muestra un esquema del aglomerador de lecho fluidizado por lotes (1) que se utilizó en este estudio, el cual es de acero inoxidable y se caracteriza por tener una sección transversal variable. El calentamiento del aire se llevó a cabo a través de un banco de 10 resistencias conectadas en serie (2). El sistema de captura y recirculación de partículas elutriadas, consistió de un ciclón de 0.1 m3 de capacidad, cuya descarga se conectó directamente a la zona de dispersión en el lecho fluidizado. Como sistema de aspersión se utilizó una boquilla neumática de mezclado interno tipo 1/4J SU11, de dos vías, operada a 2.2 bar (4). El líquido aglomerante se almacenó en un tanque presurizado (5). El aire que se alimentó al sistema fue alimentado desde un compresor, el cual está equipado con una trampa de aceite y un regulador de presión, para así garantizar condiciones constantes de suministro del aire (6). La alimentación de aire y líquido aglomerante se interrumpían mediante el cierre de una válvula solenoide que estaba acoplada al sistema de aspersión (4).

2.3 Diseño experimental
El desarrollo experimental se basó en un diseño factorial completamente aleatorizado. Este diseño consideró todas las combinaciones posibles de los niveles de los parámetros de operación. El tiempo de alimentación del líquido aglomerante (ta) varió de acuerdo a los niveles de 20, 40 y 60 min; la temperatura del aire alimentado (To) varió en los niveles de 60, 70, 80 y 90 °C; y la recirculación (R) de partículas elutriadas varío en dos niveles cualitativos que corresponden a una operación con recirculación (CR) y otra sin recirculación (SR). El análisis de las observaciones se presenta en dos secciones, la primera que comprende los experimentos SR y la segunda los experimentos CR.
2.4 Procedimiento experimental
El equipo se estabilizó térmicamente a la temperatura deseada. Se cargaron 0.3 Kg de partículas de tamarindo en la cámara de fluidización y se alimentó aire a un flujo especifico. La velocidad superficial del aire (U0) se mantuvo constante para todas las corridas y fue igual a 1.212 m/s. Bajo estas condiciones se inició el proceso de atomización del líquido aglomerante. Finalmente, al término de cada corrida experimental se interrumpe el flujo de líquido aglomerante, y se deja que el sistema fluidize durante un periodo de 5 minutos, con el objeto de obtener un aglomerado con una humedad semejante a la de las partículas iniciales.
A las partículas aglomeradas que se recolectaron de la cámara de fluidización se les determinó el diámetro promedio mediante un análisis de tamices. Se emplearon 7 mallas estándar: No. 20, 30, 40, 60, 80, 100 y 150, y una charola recolectora de los fondos. Los tamaños de abertura estaban comprendidos entre 0.841 mm y menores a 0.074 mm. Los tamices se sacudieron durante 5 minutos a una velocidad de 800 vibraciones por minuto empleando un equipo ROTAP mod. RX–29. El diámetro promedio de las partículas aglomeradas se calculó a partir de la Ec. (1) donde se relaciona la fracción masa de agregados (Ni) retenida entre los tamices i e i–1, con el promedio aritmético de las aberturas correspondientes a ambos tamices (dpi).
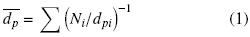
2.5 Análisis estadístico
Para determinar cualitativamente el efecto de los parámetros del proceso en la aglomeración de las partículas de tamarindo se aplicó un análisis de varianza (ANOVA) con un nivel de significancia, α, del 5% a los resultados experimentales. El diámetro promedio  se seleccionó como parámetro de respuesta.
se seleccionó como parámetro de respuesta.
2.6 Balance de población discretizado
En este trabajo se empleó un BP para describir los distintos mecanismos de aglomeración en el lecho fluidizado estudiado. En particular, se utilizó un balance de población discretizado (BPD) que se basa en el desarrollado por Hounslow y col., (1988). El cual cumple la siguiente condición de discretization para la población de partículas:

Donde r es el radio o volumen de la partícula en un intervalo (i) y en un intervalo inmediato mayor (i + 1). El BPD que se utilizó en este trabajo considera lo siguiente:
(1) Se toman en cuenta los mecanismos de nucleación, crecimiento y agregación, pero no el de rompimiento, ya que para sistemas similares, este último es muy lento con respecto a los otros y de acuerdo a diversos trabajos (Tan y col., 2005) se considera implícitamente en el término que caracteriza el mecanismo de nucleación.
(2) Se utilizan cinéticas empíricas para la nucleación y crecimiento. Mientras que para agregación se utiliza una expresión semiempírica conocida como la ecuación de equipartición de energía cinética de kernel (Ecuación 7) cuyo desarrollo se basa en la teoría cinética de los gases (Hounslow y col, 1988).
(3) Se presentan dos tipos de nucleación dependiendo del tamaño relativo entre la gota y la partícula que interactúan: de dispersión y de inmersión. Éstos se agrupan y cuantiflcan con una misma cinética de nucleación. La nucleación tiene lugar durante toda la operación del equipo (Cryer, 1999).
Por lo anterior, el BPD está descrito por las siguientes ecuaciones:

Donde Ni; es la fracción masa de agregados; t es el tiempo de operación; y βnuc, βcrec y βagreg son las constantes cinéticas de nucleación, crecimiento y agregación, respectivamente.
Los modelos en este trabajo están dados por un conjunto de ecuaciones diferenciales ordinarias que fueron resueltas por el método de Runge–Kutta–Fehlberg (Lapidus y col., 1971). La estimación de los parámetros cinéticos se llevó a cabo utilizando el método de Levenberg–Marquardt (Stewart y col., 1971).
3 Resultados y discusión
3.1 Diámetro promedio
Las partículas de tamarindo utilizadas en este estudio se clasificaron como tipo A (Geldart, D., 1973) con un diámetro inicial promedio ( ) de 0.121 mm, densidad aparente (ρa) de 1140 kg/m3 y velocidad mínima de fluidización (Umf) igual a 0.206 m/s.
) de 0.121 mm, densidad aparente (ρa) de 1140 kg/m3 y velocidad mínima de fluidización (Umf) igual a 0.206 m/s.
En la Fig. 2 se presentan las distribuciones de la fracción de partículas retenida en los tamices, a las diferentes condiciones de operación del sistema. Con el propósito de resaltar las diferencias en la distribución del tamaño de las partículas se establecieron arbitrariamente 3 intervalos: uno inferior (0.0895 a 0.127 mm), uno intermedio (0.163 a 0.335 mm) y otro superior (0.5075 a 1.42 mm). En todos los casos se muestra la distribución de partículas inicial para propósitos de comparación. En esta figura se observa que la cantidad de partículas retenidas, se desplaza del intervalo inferior hacia los superiores, lo cual sugiere que se presenta un proceso de aglomeración.
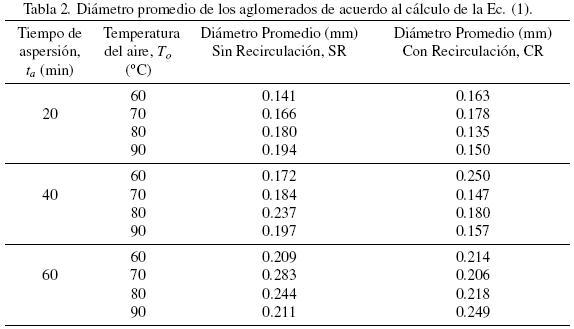
A partir de los datos de la Fig. 2 y utilizando la Ec. (1) se obtuvo el diámetro promedio correspondiente a cada corrida experimental, los cuales se muestran en la Tabla 2 y se discuten a continuación considerando dos situaciones: operación del equipo sin recirculación (SR) y con recirculación (CR) de las partículas elutriadas.
3.1.1 Experimentos sin recirculación
La primera interacción entre las gotas de líquido aglomerante y partículas suspendidas se lleva a cabo en la zona de aspersión. Las partículas al ser del tipo A, tienden a formar preferentemente núcleos saturados de líquido cuando éstas son engullidas, dominando así el mecanismo de nucleación por inmersión (Kumar, 2006). No obstante, es importante resaltar, que cuando las partículas elutriadas no se recirculan al sistema, aparentemente el fenómeno de nucleación por inmersión disminuye; tal que el líquido atomizado interactúa preferentemente con la población de partículas presentes en la zona de dispersión. El líquido humedece la superficie de las partículas, éstas una vez humedecidas, colisionan entre sí presentándose el crecimiento de la partícula por mecanismos de nucleación y/o agregación.
En la Tabla 2, se observa una tendencia a obtener partículas de mayor tamaño cuando incrementa el tiempo de aspersión, indicando que a tiempos bajos domina el mecanismo de nucleación, mientras que a tiempos altos domina el mecanismo de agregación; como se discute y corrobora más adelante en el modelado del sistema estudiado. A una temperatura de 70°C y un tiempo de aspersión de 60 minutos se obtiene el mayor crecimiento de las partículas.
La variación de la temperatura tuvo un efecto despreciable en el crecimiento del aglomerado final, comparada con el efecto de la variación del tiempo de aspersión. No obstante, la temperatura interactuó de manera compleja con el sistema de granulación, ya que para cada tiempo de aspersión tuvo un efecto diferente en el diámetro promedio del producto final. Para un tiempo de aspersión alto, el incrementar la temperatura redujo el diámetro promedio, lo que se relacionó principalmente con su contribución a la pérdida de resistencia de partículas aglomeradas, ya que aparentemente una temperatura alta favoreció el nivel de evaporación del líquido que actúa como ligante, existiendo una deficiencia de líquido en la superficie de las partículas e impidiendo el establecimiento de los puentes líquidos, y por consiguiente disminuyendo el mecanismo de agregación. A tiempos de aspersión bajos, se presenta una tendencia a incrementar el diámetro del aglomerado al incrementar la temperatura. En este caso, puede entenderse que conforme incrementa el tamaño del aglomerado, el líquido que se deposita en la superficie tiende a penetrar hacia el interior de éste, por consiguiente, al colisionar las partículas, el puente líquido que se establece en el punto de contacto es lo suficientemente fuerte para mantenerlas unidas, favoreciendo el mecanismo de agregación.
3.1.2 Experimentos con recirculación
El efecto de recircular las partículas elutriadas nuevamente al sistema prolonga el contacto entre las partículas de menor tamaño y el líquido atomizado, existiendo durante toda la operación del granulador un mecanismo de nucleación por inmersión en la en la zona de aspersión como lo sugiere Realpe y Velásquez (2008). Los resultados que se presentan en la Tabla 2 para los experimentos con recirculación muestran que el tiempo de aspersión tuvo el efecto más significativo en la aglomeración de las partículas, teniendo el mayor tamaño cuando se operó el granulador con un tiempo de aspersión de 60 minutos y temperatura de 90°C. El efecto de la temperatura no es claro pero, como se corrobora en el análisis de varianza y en el modelado del sistema en subsecuentes secciones, no presenta un efecto apreciable comparado con el del tiempo de aspersión en la formación del aglomerado.
En términos generales, la operación del sistema con y sin recirculación de partículas elutriadas a la cámara de fluidización no tiene un efecto considerable en el proceso de aglomeración, si es comparado con el efecto del tiempo de aspersión. No obstante, se observa que se obtienen aglomerados de un tamaño más uniforme cuando se recirculan los sólidos.
Un aspecto a resaltar es con relación a la población de partículas consideradas en los intervalos inicial e intermedio, la cual disminuye debido a que pasan a formar parte de la población de partículas de los intervalos superiores. Esta disminución, sugiere que la constante de formación de núcleos en la zona de aspersión debido a la recirculación de partículas a la cámara de fluidización que al mezclarse en la zona de dispersión, colisionen con otras partículas, incrementado la población de partículas de los intervalos superiores (Goldszal y Bousquet, 2001; Kumar, 2006; Realpe y Velásquez, 2008).
4 Análisis de varianza
En la Tabla 3 se presenta el resumen del análisis de varianza (ANOVA) aplicado a los resultados obtenidos del diseño experimental. El análisis estadístico evaluó los datos a un nivel de significancia, α, del 5%. En esta tabla se muestra el valor de la distribución calculada, "Fo" y la distribución teórica, "Fteórica". De tal forma que, si estas distribuciones son comparadas, y Fo > Fteórica significa que existe una diferencia en las respuestas al variar los niveles de los parámetros del proceso bajo estudio. De manera alterna se puede emplear el enfoque de probabilidad "P" que indica si los datos son significativos. Por consiguiente, al analizar estos valores para los diferentes parámetros del proceso se observa que la variación del tiempo de aspersión del liquido aglomerante es la variable que más afecta el crecimiento del aglomerado: Fo = 9.48 > Fteórica = 5.14, (P < 0.05). Cabe resaltar, que este hecho se visualizó al realizar el análisis de la variabilidad del diámetro promedio por efecto de los parámetros del proceso estudiados, y se confirma por medio del análisis de varianza y el modelado del sistema.
5 Análisis de las predicciones
El modelo descrito por las ees. (3)–(7) se utilizó para describir el comportamiento de varios experimentos que representan el efecto de los distintos parámetros del proceso sobre los diferentes mecanismos de aglomeración: ta (20 min y 60 min), T (60°C y 80°C), R (CR y SR). En la Tabla 4 se muestran los valores de las constantes cinéticas βnuc, βcrec y βagreg, que fueron estimadas utilizando las observaciones correspondientes a cada corrida experimental. La magnitud de estas constantes cinéticas se relacionaron directamente con la contribución de los mecanismos de aglomeración considerados en el modelo: nucleación, crecimiento y agregación. Los valores estimados presentaron un 95% de confiabilidad y no presentaron una correlación estadística entre ellas (CE<0.8).

El análisis del valor de las constantes cinéticas concuerdan con el análisis de varianza, mostrando que variaciones en la temperatura y la operación del sistema CR y SR de elutriados no provocan un efecto apreciable en los mecanismos de aglomeración. Aunado al hecho que para todos los casos estudiados, el mecanismo de crecimiento fue despreciable con respecto a los de nucleación y aglomeración. Así el tiempo de aspersión es el parámetro del proceso que influye en mayor grado el aglomerado de las partículas: a tiempos de aspersión cortos, el mecanismo de nucleación es dominante; mientras que a tiempos de aspersión largos lo es la agregación. Esto se puede relacionar con el hecho de que en la zona de aspersión se tienen una población de partículas finas importante a tiempos de aspersión bajos: dominando el fenómeno de nucleación. De tal forma que a tiempos de aspersión largos estas partículas finas se consumen y el mecanismo de agregación domina el proceso.
La Fig. 3 muestra una comparación entre predicciones y observaciones de la distribución de partículas para dos diferentes tiempos de aspersión, considerando para ambos casos la misma distribución de partículas inicial, la misma temperatura y condiciones de recirculación de elutriados (CR). La Fig. 3a muestra la dinámica de aglomeración para un tiempo de aspersión de 20 minutos. El modelo predice satisfactoriamente las observaciones al final de la operación del granulador, donde se observa la dinámica de formación de núcleos como mecanismo dominante de aglomeración. La Fig. 3b muestra una comparación entre la distribución de partículas a dos tiempos de aspersión: 20 y 60 minutos. El modelo además de predecir las observaciones satisfactoriamente, concuerda con lo expuesto arriba en términos de las constantes cinéticas y el análisis de varianza: la variación del tiempo de aspersión tiene el mayor efecto en el proceso de aglomeración. Aquí, la nucleación es el mecanismo dominante a tiempos de aspersión bajos mientras que la agregación lo es a tiempos de aspersión altos. Las figuras, para los otros casos de estudio, no mostradas en este trabajo, corroboran los resultados discutidos arriba en términos de las constantes cinéticas.

Conclusiones
Este trabajo mostró que la aglomeración de partículas orgánicas en un granulador de lecho fluidizado a escala piloto puede ser estudiado satisfactoriamente con el uso e integración de herramientas estadísticas y fundamentales, como son un diseño experimental, un análisis estadístico y un balance de población discretizado, que permiten analizar y cuantificar el efecto de los parámetros del proceso ta, To y recirculación de partículas elutriadas, sobre los diferentes mecanismos presentes en la aglomeración: nucleación, crecimiento, agregación, etc.
El análisis cualitativo de las observaciones mostró la presencia de un crecimiento de las partículas conforme aumentó el tiempo de adición del agente aglomerante. A las condiciones hidrodinámicas establecidas, el lecho de partículas es agitado suficientemente para distribuir el líquido y permitir que las partículas de menor tamaño sean suspendidas, por consiguiente, la aglomeración se vio influenciada por el tamaño relativo de las partículas en la zona de aspersión. Aunado al hecho, de que una adecuada relación entre el liquido atomizado y flujo de aire permite una mayor concentración de líquido en el lecho, sin que se presente el fenómeno de apagado húmedo, lo que se reflejó en un mayor crecimiento de las partículas.
El análisis de varianza y el uso de un balance de población discretizado confirman la influencia significativa del tiempo de atomización sobre los diferentes mecanismos de aglomeración: la nucleación es el mecanismo dominante a tiempos de aspersión bajos, mientras que la agregación lo es a tiempos de aspersión altos; el mecanismo de crecimiento fue despreciable.
Nomenclatura

Referencias
Ayazi, S. P, Liu, Z. y Yates, GJ. (1990). Hydrodynamic influences on particle breakage in fluidized beds. Chemical Engineering Science 45 (4), 809–817. [ Links ]
Cryer, A. S. y Scherer, N.R (2003). Observations and process parameter sensitivities in fluid–bed granulation. AIChE Journal 45 (10), 2069–2078. [ Links ]
Cryer A. S. (1999). Modelado de procesos de aglomeración en lechos fluidizados. AIChE Journal 45 (10), 2069–2078. [ Links ]
Dacanal, G.C. y Menegalli, F.C. (2008). Experimental study of fluidized bed agglomeration of acerola powder. Brazilian Journal of Chemical Engineering 25 (1), 51–58. [ Links ]
Davidson, J. F., Clift, R. y Harrison, D. (1985). Particle Growth and Coating in Gas– Fluidized Beds en: Fluidization, (A.W. Nienow y P.N. Rowe), 563– 594. Academic Press, U.K. [ Links ]
Geldart, D. (1973). Types of gas fluidization. Powder Technology 7 (5), 285–292. [ Links ]
Goldszal, A. y Bousquet, J. (2001). Wet agglomeration of powders: From physics toward process optimization. Powder Technology 117 (3), 221–231. [ Links ]
Hulbert, H. y Katz, S. (1964), Some problems in particle technology. A statistical mechanical formulation. Chemical Engineering Science 19, 555–574. [ Links ]
Hounslow, M.J., Ryall, R.L. y Marshall V.R. (1988). A discretized population balance for nucleation, growth and agregation. AIChE Journal 34 (11), 1821–1832. [ Links ]
Iveson, S.M., Lister, J.D., Hapgood, K. y Ennis, B.J. (2001). Nucleation, growth and breakage phenomena in agitated wet granulation processes: A review. Powder Technology 117 (1–2), 3–39. [ Links ]
Kumar, J. (2006). Numerical Approximations of Population Balance Equations in Particulate Systems. Dissertation, genehmigt durch die Fakultät für Mathematikder Otto–von–Guericke–Universität Magdeburg. [ Links ]
Kumar, S. y Ramkrishna, D. (1997). On the Solution of population balance equations by discretization–III. Nucleation, growth and aggregation of particles. Chemical Engineering Science 52(24), 4659–4679. [ Links ]
Lapidus, L. y Seinfeld, J.H. (1971). Numerical Solution of Ordinary Differential Equations. Editorial. A. Press., Nueva York. [ Links ]
Lister, J.D. y Ennis, B. (2004). The Science and Engineering of Granulation Processes. Kluwer Academy Publishers, Dordrecht. [ Links ]
Montgomery, C. D. (2007). Diseño y Análisis de Experimentos. John Wiley & Sons Ltd. [ Links ]
Nienow, A. W. y P.N. Rowe. (1985). Particle Growth and Coating in Gas–Fluidized Beds, Fluidization. Academic Press, Londres. [ Links ]
Poon, J. M. H., Immanuel, C. D., Doyle, I. I. I. F. J. y Litster, J. D. (2008). A three–dimensional population balance model of granulation with a mechanistic representation of the nucleation and aggregation phenomena. Chemical Engineering Science 63(5), 1315–1329. [ Links ]
Realpe, A. y Velásquez, C. (2008). Growth kinetics and mechanism of wet granulation in a laboratory–scale high shear mixer: Effect of initial polydispersity of particle size. Chemical Engineering Science 63 (6), 1602–1611. [ Links ]
Rhodes, M. J. (1998). Introduction to Particle Technology. John Wiley & Sons Ltd, México. [ Links ]
Ríos, M. D. (2005). Aglomeración de Finos en un Sistema Combinado Aspersión–Fluidización. Tesis de Maestría en Ciencias en Ingeniería Química, Universidad Autónoma Metropolitana, México. [ Links ]
Schaafsma S.H. y Kossen, N.W.F. (1999). Effects and control of humidity and particle mixing in fluid–bed granulation. AIChE Journal 45 (6), 1202–1210. [ Links ]
Schaafsma S.H., Kossen, N.W.F., Mos, T. M. y Hoffman A. C. (2006). A Model for the spray zone in early–stage fluidized bed granulation. AIChE Journal 52 (8), 2736–2741. [ Links ]
Schaafsma S. H., Vonk P. y Kossen N.W.F. (2000). Fluid bed agglomeration with a narrow droplet size distribution. International Journal of Pharmacology 193, 175–187. [ Links ]
Stewart W.E., Caracotsios M. y Sørensen J.P. (1992). Parameter estimation from multiresponse data: GREGPACK. AIChE Journal 38 (5), 641–650. [ Links ]
Soos, M., Sefcik, J. y Morbidelli, M. (2006). Investigation of aggregation, breakage and restructuring kinetics of colloidal dispersions in turbulent flows by population balance modeling and static light scattering. Chemical Engineering Science 61 (8), 2349–2363. [ Links ]
Tan, H.S., Salman, A.D. y Hounslow, M.J. (2006). Kinetics of fluidized bed melt granulation I: The effect of process variables. Chemical Engineering Science 61 (5), 1585–1601. [ Links ]
Tan, H. S., Salman, A. D. y Hounslow, M. J. (2005). Kinetics of fluidized bed melt granulation V: Simultaneous modelling of aggregation and breakage. Chemical Engineering Science 60 (14), 3847–3866. [ Links ]
Tourbin, M. y Frances, C. (2008). Experimental characterization and population balance modelling of the dense silica suspensions aggregation process. Chemical Engineering Science 63 (21), 5239–5251. [ Links ]
Waldie, B. (1991). Growth mechanism and the dependence of granule size on drop size in fluidized–bed granulation. Chemical Engineering Science 46 (11), 2781–2785. [ Links ]














