Working towards algebra: the importance of relational thinking

Stephens, Max; Ribeiro, Alessandro

Services on Demand

Journal

Article

Indicators

Cited by SciELO
Access statistics

Revista latinoamericana de investigación en matemática educativa

On-line version ISSN 2007-6819Print version ISSN 1665-2436

Relime vol.15 n.3 Ciudad de México Nov. 2012

Artículos

Working towards algebra: the importance of relational thinking

Max Stephens*, Alessandro Ribeiro**

* The University of Melbourne, Australia. m.stephens@unimelb.edu.au

** Universidade Federal do ABC, Brazil. alessandro.ribeiro@ufabc.edu.br

Recepción: Junio 21, 2011
Aceptación: Septiembre 5, 2012.

RESUMEN

El álgebra se ha convertido en un elemento esencial para tener éxito en matemáticas. En este artículo argumentamos que, para que los estudiantes puedan desarrollar adecuadamente su comprensión del álgebra, es necesario construir unos fundamentos sólidos en la educación primaria y secundaria a través de experiencias con operaciones numéricas, así como con las ideas clave de equivalencia y compensación. Estos fundamentos son generalmente descritos por el término pensamiento relacional. Este estudio explora sobre el pensamiento matemático de algunos estudiantes de los grados 7 y 8 en Brasil. Se encontró que la mayoría de los estudiantes prefiere utilizar métodos computacionales al momento de resolver expresiones numéricas usando cuatro operaciones aritméticas. Sin embargo, cuando se les pidió evidenciar el pensamiento relacional, la mayoría de los estudiantes lo demuestran, sin embargo, es claro que necesitan mas apoyo en este aspecto.

PALABRAS CLAVE: Pensamiento, algebraico Pensamiento relacional, Justificación, Reforma del programa, Implicaciones para la enseñanza.

ABSTRACT

Algebra has become a building block for success in mathematics. Our argument in this paper is that, in order to allow students to properly develop their understanding of algebra, solid foundations need to be laid during elementary and junior secondary school years through experiences with number operations and the key ideas of equivalence and compensation. These foundations are broadly described by the term relational thinking. In this exploratory study of the mathematical thinking of a selection of Year 7 and Year 8 students in Brazil, we found that when students were asked to solve numerical expressions using four arithmetic operations, most students opted for computational methods. However, when required to show relational thinking, most students did so, but clearly needed further support in this respect.

KEY WORDS: Algebraic thinking, Relational thinking, Justification, Curriculum reform, Implications for teaching.

RESUMO

A Álgebra tornou-se um elemento essencial para o sucesso em matemática. Nossa argumentação neste artigo explica que os estudantes necessitam de sólidos fundamentos na educação básica e, desta forma, situálos em um melhor entendimento algébrico que esteja baseado em experiências prévias com operações numéricas, assim como com ideias - chaves de equivalência e de compensação. Estes fundamentos são ampiamente descritos por meio da ideia de pensamento relacional. Neste estudo exploratório do pensamento matemático de estudantes de 7º e 8º anos no Brasil, encontramos evidências de que, quando os alunos resolvem sentencas numéricas por meio das quatro operações, a maior parte deles opta por métodos computacionais. E, quando são questionados para ''mostrar'' o pensamento relacional, a maior parte deles o faz, mas verificou-se que eles, claramente, precisam de suporte.

PALAVRAS CHAVE: Pensamento algébrico, Pensamento relacional, Justificação, Reforma curricular, Implicações para o ensino.

RÉSUMÉ

L'algèbre est devenue un élément essentiel pour la réussite en mathématiques. Dans cet article, nous défendons le fait que pour que les élèves puissent être en mesure de progresser dans leur compréhension de l'algèbre, il est primordial de leur fournir, dès l'école élémentaire et tout au long de l'école secondaire, des bases solides en ce qui concerne les opérations élémentaires ainsi que les notions clés d'équivalence et de compensation. De telles bases sont généralement décrites en termes de raisonnement relationnel. Notre étude préliminaire, menée auprès d'élèves de sixième et de cinquième au Brésil, semble indiquer que pour résoudre des expressions numériques avec les quatre opérations, la plupart des élèves choisissent des méthodes numériques. Pourtant, lorsqu'on le leur demande, la plupart des élèves sont capables de détailler leur raisonnement relationnel mais ils ont alors clairement besoin d'une aide supplémentaire.

MOTS CLÉS: Raisonnement algébrique, Raisonnement relationnel, Justification, Réforme des programmes scolaires, Implications pour l'enseignement.

1. RATIONALE

Research on the development of algebraic thinking is urgently needed. According to The Mathematical Association of America (Katz, 2007), Algebra: Gateway to a Technological Future, it is said that ''We need a much fuller picture of the essential early algebra ideas, how these ideas are connected to the existing curriculum, how they develop in children's thinking, how to scaffold this development, and what are the critical junctures of this development'' (p.2). For this reason, researchers need to construct problems that are carefully sequenced across several problem types in order to identify key steps in the development of the students' understanding of algebraic processes. The following missing-number sentences, for example, permit students to use a range of solution strategies, and to reveal their mathematical thinking.

How might students think about these kinds of problems? What numbers could be in the Box(es)? How do you find the missing numbers in these mathematical sentences?

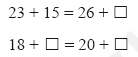
Firstly, we can expect that some students will employ purely computational methods to solve number sentences like the two given above. Our goal is to move students beyond purely arithmetic approaches to thinking about the kind of relationships that exist between the numbers. In the first number sentence, one number satisfies the relationship. In the second sentence, there are many possible solutions and different ways of describing those solutions. The focus of this paper is to identify and analyze several kinds of problems with a high potential for revealing and developing students' understanding of mathematical relationships.

2. RECENT RESEARCH ON RELATIONAL THINKING

Stephens (2007) reported that when using Computational Thinking, students first recognize the field the problem belongs to, and then activate a series of computational procedures they have already mastered to find the answer. In solving the following number sentence:

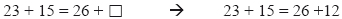
Working from the left side where the known numbers are placed, a student might carry out the following calculation:

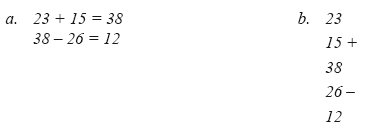
Another quite different solution would be the following: Since the relationship between 23 and 26 is 3 more, in order for both sides to be equal, it has to be a number that is 3 less than 15. Therefore, the number in the ''empty'' box must be: 15 - 3 = 12. We have called this kind of thinking relational thinking. The following diagram illustrates the relational thinking process as mentioned above.

The term ''relational thinking'' (pensamiento relacional) has received currency from researchers such as Carpenter and Levi (1999), Molina, Castro, and Ambrose (2006) and Jacobs, Franke, Carpenter, Levi, and Battey (2007). The latter authors make the point that there is still room for debate as to whether relational thinking in arithmetic represents a way of thinking about arithmetic that provides a foundation for learning algebra or is itself a form of algebraic reasoning, and conclude that ''one fundamental goal of integrating relational thinking into the elementary curriculum is to facilitate students' transition to the formal study of algebra in the later grades so that no distinct boundary exists between arithmetic and algebra'' (p. 261).

According to Molina, Castro, and Mason (2008), students using this kind of thinking, are able to consider the number sentence as a whole, and then analyze the mathematical structure and important elements of the sentence to generate productive solutions. Other research from Carpenter and Franke (2001) and Stephens (2007, 2008) refer to relational thinking in the same way; i.e. when students see the equals sign as a relational symbol, they can focus on the structure of expression, and carry out reasonable strategies to solve the number sentence pursuant to the operations involved.

Five key ideas underpin our theoretical position on relational thinking which constitutes a bridge between number and number operations and early algebra thinking. These key ideas are all now prominent in research literature on early algebra:

- Structure of number sentences (Cai, Ng, & Moyer, 2011; Jacobs et al., 2007);

- Equivalence (Kaput, Carraher, & Blanton, 2008; Molina, Castro & Ambrose, 2006; Lins & Kaput, 2004; Kieran, 1981);

- Variation and compensation using equivalence according to specific operations (Britt & Irwin, 2011; Stephens & Wang, 2009; Irwin & Britt, 2005);

- Numbers that can vary (Cooper & Warren, 2011; Fujii & Stephens, 2001); and

- Generalization (Cooper & Warren, 2011; Mason, Stephens & Watson, 2009).

Skemp's (1976) important distinction between relational and instrumental understanding supports the ideas presented here in a general way, in that it distinguishes between two broad ways of thinking about and doing mathematics. However, it does not constitute a definition of relational thinking as we and the above authors present it. The five key ideas each require a deeper understanding of number sentences and are often left implicit in the textbook treatment of algebra in junior secondary school, where algebra is introduced as the generalization of arithmetic and formal use of letters in equations. Moreover, assessment frequently emphasizes procedural fluency assuming that procedural success carries with it conceptual understanding.

Moving from an operational to a relational conception of the equals sign has been rightly emphasized by Kieran (1981) and more recently by Molina, Castro and Ambrose (2006) and Molina, Castro and Mason (2008). However, the key role of equivalence in relational thinking needs to embrace the other key ideas discussed above. Unless students experience these key ideas in the context of number sentences and number operations during elementary and junior secondary years, our argument is that they will usually have a difficult transition to learning algebra in junior secondary school. As Cooper and Warren (2011) argue, ''quasi-generalisation in an elementary (school) context appears to be a necessary precursor to expressing the generalisation in natural language and algebraic notation'' (p. 193).

Currently, in the curriculum documents of many countries, there is a clear movement towards developing a more coherent approach between the study of number and number operations during elementary and junior secondary years and the development of algebraic thinking. For example, the Australian Curriculum: Mathematics developed by the Australian Curriculum and Reporting Authority (ACARA, 2010) presents Number and Algebra as a single content strand for compulsory years of school. China's Mathematics Curriculum Standards for Compulsory Education (Ministry of Education, 2001; 2011) also present a single strand entitled Number and Algebra. This trend is endorsed by the National Council of Teachers of Mathematics (USA) Curriculum Focal Points (NCTM, 2006), where it is advocated that instructional programs from pre-kindergarten through Grade 12 should enable all students to understand patterns, relations, and function. In Grades 6-8 all students should represent, analyse, and generalize a variety of patterns with tables, graphs, words, and, when possible, symbolic rules; relate and compare different forms of representation for a relationship; identify functions as linear or nonlinear and contrast their properties from tables, graphs, or equations.

3. ALGEBRA AND ALGEBRAIC THINKING IN BRAZIL'S NATIONAL CURRICULUM

Brazil's National Curriculum Standards for Elementary School (Ministerio da Educacao Brasil, 1998) also emphasize the importance of fostering mathematical algebraic thinking through work and activities involving different perspectives and ways of conceiving Algebra. These situations can be exemplified as ''working towards algebra''. They may not be Algebra itself as seen in high school textbooks, but they are clearly intended as such, as the following quote from Brazil's curriculum guidelines shows: to ''grow algebraic thinking'' out of students' experience of arithmetic.

''Generalized arithmetic'', ''functional'', ''equations'' and ''structural'' according to the letters are considered respectively as ''generalizations of the arithmetic model,'' ''variables to express relationships and roles'', ''unknown'', ''abstract symbols'' (Ministerio da Educacao Brasil, 1998, p. 116).

The intention behind such terms as ''generalized arithmetic'' and ''generalizations of the arithmetic model'' necessarily requires teachers to direct students' attention to mathematical features that are embedded in arithmetic - its operations and relationships - thus stepping away from an exclusive focus on calculation. In these ways, the guidelines ''walk towards'' working with Algebra and thinking algebraically in different ways and with different approaches. The guidelines recommend that teachers use problems ''that allow them [students] to give meaning to language and mathematical ideas'' (Ministerio da Educacao Brasil, 1998, p. 84). The same documents give a clear emphasis to the critical importance of algebra in opening up many ideas that are key to later success in mathematics.

At work with Algebra is fundamental to understanding concepts such as variable and function, the representation of phenomena in algebraic form and in graphical form, the formulation and problem solving by equations (to identify parameters, unknowns, variables) and knowledge of the ''syntax'' (resolution rules) of an equation (Ministerio da Educaçao Brasil, 1998, p. 84).

We agree with this emphasis on algebra being a gateway to mathematics. For many who leave elementary school with a limited and incomplete development of algebraic thinking, the study of Algebra in high school serves regrettably as a building block for success in mathematics and serves to close off many options beyond school. The guidelines of the National Curriculum of Secondary School (Ministerio da Educacao Brasil, 2000) support our view that mathematics is - or should be - the gateway to important ways of thinking throughout school life and beyond. The uses of these ideas for the training and academic-scientific-cultural life of our students are set out clearly below where mathematics is seen as having:

a formative value, which helps to structure thinking and deductive reasoning, but also plays an instrumental role [...] In this formative role, Mathematics contributes to the development of thought processes and the acquisition of attitudes, whose usefulness transcends Mathematics, can form in the student's ability to solve genuine problems, generating research habits [...] As for the instrumental character of mathematics in high school, it should be seen by the student as a set of techniques and strategies to be applied to other areas of knowledge, as well as professional activity [... ] However, high school mathematics not only has the formation or instrumental characters, but should be seen as a science, with its specific structural features. It is important that students realize that the definitions, statements and conceptual and logical chains have the task of constructing new concepts and structures from others and serve to validate intuitions and make sense of the techniques applied. (Ministerio da Educacao Brasil, 2000, p. 40-41).

Endorsing these ideas, we argue for the need to develop continuities and convergences between elementary school mathematics and the highly valued forms of thinking discussed above. Any evidence of discontinuities in students' actual thinking, as we will show, must be seen as a challenge to curriculum planners and teachers in order to build stronger bridges between students' experience of number and number operations in elementary school and the concurrent goal of providing sound foundations for the development of mathematical algebraic thinking.

4. AN EXPLORATORY STUDY OF RELATIONAL THINKING IN YEARS 7 AND 8

This exploratory study of relational thinking was conducted in two different schools in São Paulo, Brazil, involving 14 students in Year 8 and 30 students in Year 7. For these students, our questions were intended to probe, i.e. to carry out an in-depth study of students' capacity to engage in relational thinking, and therefore needed to encompass all four operations. The questionnaire used three distinct types of sentences/problems: firstly, single value number sentences (Type I) that may be solved computationally or relationally; and two-value number sentences (Type II) where the students were required to think about numbers that can vary. It also introduced students to simple symbolic sentences (Type III) modelled on the second type of number sentence. As far as their explanations were concerned, students could use different representations, but we expected written explanations to be the most common acceptable form of justification.

An eight-page questionnaire was used consisting of four separate sections covering each of the four arithmetical operations. The questionnaire was translated into Portuguese from an English version that had been developed by one of the authors. This same questionnaire had also been used successfully in several other countries, including China (Stephens & Wang, 2008) and Indonesia (Stephens & Armanto, 2010). Four Type I number sentences (single box) were used for each operation. Each set was preceded by the sentence: ''For each of the following number sentences, write a number in the box to make a true statement. Explain your working briefly.'' In each set, the empty box denoting the missing number to be found was placed in a different position each time.

The following sample of Type I problems shows one problem only for each operation:

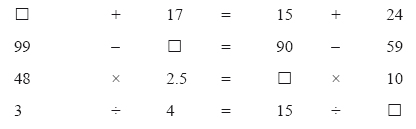
In each of the above examples, computational thinking requires the student to work out the ''known part'' of the sentence, that is 15 + 24; or 90 - 59; or 48 x 2.5; or 3 ÷ 4; and then to use the answer to this known part to calculate the value of the missing number. In the third question, for example, having obtained 120 as the result of multiplying the two known numbers, the student has to think about the numbers on the other side of the equal sign, asking ''What is multiplied by 10 to give 120?'' or ''If I divide 120 by 10 what do I get?'' - leading to an answer of 12. This kind of computational thinking is both accurate and efficient, but it is fundamentally different from relational thinking where the focus is on the whole sentence - and its two equivalent parts - and identifying a pattern of variation based on the operations involved (see Irwin & Britt, 2005). To illustrate relational thinking in the third sentence, Irwin and Britt (2005) suggest that a student might reason as follows: ''I can see that 10 is four times 2.5, so for both sides to be equivalent, the 48 has to be divided by 4. The missing number is therefore 12.''

Irwin and Britt (2005) draw attention to the fact that relational thinking is not simply about equivalence as shown by the presence of the ''='' sign. They argue that, in order to use equivalence between the two related parts of number sentences, like the four given above, in order to find the value of a missing number, one has to know the direction in which compensation needs to occur. In addition and subtraction, the direction of compensation is different. Similarly, the direction of compensation is different between multiplication and division. Irwin and Britt (2005) explain that relational thinking requires the student to identify both the numbers that are ''related'' and the ''operation'' involved. Relational thinking is not possible if, for example, one tries to relate the 48 and the 10. In the case of the second sentence, a key issue is knowing that subtraction is different to addition. Therefore, if 99 is nine more than 90, the missing number has to be nine more than 59 for both sides to remain equivalent. Some students, as Irwin and Britt (2005) point out, confuse the direction of compensation under subtraction with the direction of compensation for addition; and conclude incorrectly that the missing number has to be nine less than 59.

The scientific purpose of using these Type I questions with students in Years 7 and 8 was to see if they could understand and use a basic sense of equivalence where a pair of numbers are represented on both sides of the equals sign using the same operation. With younger children, Molina, Castro and Mason (2008) found that, when given a Type I number sentence like , some students gave 18 or 26 as the value of the missing number, showing that they misunderstood the equals sign to indicate the answer to a calculation. We expected that almost all students in our sample had moved beyond this misunderstanding, and that many of them could find a correct answer to Type I sentences, either by computation or by using relational thinking. We anticipated that some students would show clear evidence of relational thinking, even if it was not required to solve the 16 Type I sentences they were given.

4.1. Responses to Type I sentences

In Table I below, we present a summary of students' responses to Type I sentences for Addition, Subtraction, Multiplication and Division. For each operation, the responses are classified under five headings: Computational where students showed clear evidence of carrying out a computation leading to a correct answer for the missing number; Relational where students showed clear evidence of using relational thinking to obtain a correct result; Without Justification where students wrote a correct answer but failed to give any explanation; Wrong Answers whether as a result of attempted relational or computational thinking, or with no accompanying explanation; No Attempt where the question was left blank. The numbers in Table I below represent a summary response across the four sub-questions for each operation using Type I sentences.

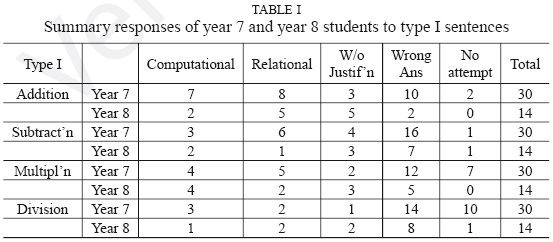
From the above table, one thing that becomes clear is the increasing number of wrong answers and no answers, especially among Year 7 students, as they moved from Addition through to the other operations. It is highest in the case of Division. In the latter case, these two categories represent 75% of all responses. It may also have been the case that some Year 7 students ran out of time completing the last parts of the questionnaire. Almost all incorrect responses appeared to be due to calculation mistakes. There was no evidence of the type of misconceptions reported by Molina et al. (2008) which were referred to earlier.

Inspection of the data for the other three headings, which together encompass correct responses, shows that Type I Addition questions were most likely to produce a correct response, with 30 of the 44 students providing correct answers. Subtraction and Multiplication are clearly more difficult with 20 or less of the sample giving correct responses. Division sentences were hardest of all with only one quarter of the students, 11 out of the 44, being able to give a correct response. These evident difficulties experienced by students in working with the four operations on relatively simple tasks are a cause of concern in working towards algebra. Any attempt at ''generalizing from the arithmetic model'' simply assumes that students understand and are confident in using arithmetic.

What do the above responses tell us about students' capacity to engage in relational thinking? It is not so easy to draw conclusions from the above data - for two reasons. The first reason is the presence of responses Without Justification. Here, one cannot be sure what the student has done in order to arrive at a correct answer. The number of responses Without Justification is, however, relatively small, showing that many students did take seriously the request to explain their own thinking. The second reason arises from the nature of Type I sentences. Those who gave a correct response using computation may be able to think relationally - we cannot be certain. In some cases, a computational response may be a result of choosing to work computationally by students who if directed could also work relationally. The nature of these Type I questions left the choice of methods open. On the other hand, some students may have used a computational method because it is the only method they have. If one made the very optimistic assumption that all those who gave a computational response could give, if asked, a relational response, the proportion of actual and potential relational responses would only reach 50% for Addition; 27% for Subtraction; 34% for Multiplication; and 18% for Division. On the other hand, if one relied only on explicitly relational responses, the proportion of demonstrated relational responses is much lower - 30% for Addition; 16% for Subtraction and Multiplication; and only 11% for Division.

Two consequences follow from what may appear to be an inconclusive analysis of these responses to Type I sentences. The first is that a differently designed sentence is needed in order to carry out a more in-depth study of students' relational thinking. For this reason, we decided to include sentences, hereinafter called Type II and Type III sentences, in the questionnaire where students are required to express their thinking relationally, and also where the format of the questions limits the possibility of Without Justification responses. The second consequence is to remind teachers that, while Type I sentences have certain limitations when used in a research questionnaire, their potential in teaching and learning is too important to neglect. Their pedagogical value in giving students alternative pathways to demonstrate why their calculations are correct is too important to ignore. However, even more importantly from the perspective of this paper, Type I sentences allow students to ''generalize from the arithmetic model'', building up a deeper understanding of equivalence and how its interpretation and enactment depends on the operations being used. This benefits students' knowledge of number and number operations, as well as working towards algebra.

4.2. Introducing Type II and Type III sentences

The two other kinds of mathematical sentences used in the questionnaire are called Type II and Type III sentences. Type II and Type III sentences encompass the four operations addition (+), subtraction (-), multiplication (x), and division (÷). Unlike Type I sentences that can be readily solved by computation, these mathematical sentences require students to think relationally. The following Type II number sentence, consisting of parts (a) to (d), was given to the students for addition:

1. Can you think about the following mathematical sentence?

(a) In each of the sentences below, can you put numbers in Box A and Box B to make each sentence correct?

(b) When you make a correct sentence, what is the relationship between the numbers in Box A and Box B?

(c) If instead of 18 and 20, the first number was 226 and the second number was 231 what would be the relationship between the numbers in Box A and Box B?

(d) If you put any number in Box A, can you still make a correct sentence? Please explain your thinking clearly.

(e) What can you say about c and d in this mathematical sentence?

c + 2 = d + 10

A Type III sentence is shown in part e above, where the symbols c and d are used in a sentence that is structurally similar to, but not identical with their corresponding Type II Number Sentence (see Table II). Following Hart (1981), students were asked: What can you say about c and d in this mathematical sentence? Students needed to describe the relationship between c and d that permits this mathematical sentence to be true. The total length of the questionnaire was eight pages.

In answering part a, we assumed that almost all students could create true mathematical sentences for all four operations. This would be possible using a basic definition of equivalence in which the result of a calculation on the left side of the equal sign has to be equal to the result of the one on the right of the equal sign. For Type II number sentences, a first scientific question was used to investigate how well students could describe how the numbers in the two Boxes varied according to the particular sentence and its corresponding operation. As a result, it was essential to classify the different ways in which students described the relationships between the numbers in the respective Boxes in order for a given sentence to be true. Concerning Type II number sentences, a second scientific question was to investigate how well students could generalise a condition under which these Type II sentences could be true for a given operation regardless of what number was used in Box A. A third scientific question was to examine if students could transfer their relational understanding of Type II number sentences to related Type III sentences involving literal symbols but with a similar mathematical structure to the Box A and Box B (Type II) sentences. Fourthly, we needed to investigate if students' responses to particular subquestions could predict the likelihood of their success or lack of success on subsequent sub-questions. Rather than arguing that this or that sub-question was ''a good question'', our aim was to show how well our sequence of staged sub-questions for each operation was effective in disclosing students' relational thinking.

In order to answer the Type II problems, key elements to look for in students' responses include:

- Were correct exemplifications given in part a?

- How did students describe the relationship between the numbers in Box A and Box B in parts b and c?

- How did responses to parts b and c assist students in generalising the relationship between numbers in Box A and Box B and how did they express that generality in part d?

In order to answer the Type III problems (part e), some key elements to look for in students' responses include:

- Were incorrect exemplifications given in part e?

- Were correct exemplifications for c and d given but no generalisation (specific values only, possibly multiple values)?

- Were some aspects of the relationship identified but not a complete description?

- Was a correct generalisation of the relationship between c and d (symbolic expression and/or correct written description) provided in part e?

In examining students' attempts at justifying their solutions to the Type II and Type III sentences, we developed a set of categorizations to describe students' answers. Apart from the Non-Relational category, the other categories show elements of Relational Thinking in different respects. As far as they are concerned, only the category, Fully Referenced and directed Relational thinking, describes a complete response. The others contain elements of relational thinking but fall short in one or more respects, as shown in the descriptions and examples given in Table III:

A Non-Relational response is evident when students do not see connections between the numbers involved in Parts b, c, d and e. This is illustrated by a student who answered Part b by saying: ''Meets the relation that the sum is the same''; and Part d by saying: ''Cannot, because if any number is filled in, it's very easy to have incorrect (numbers) filled in.''

An Incorrect relationship is shown when students incorrectly say that Box A or Box B, or c or d is larger or smaller, or use an incorrect term to describe the mathematical relationship.

A Non-directed Relationship may or may not refer specifically to Box A or Box B, or to c or d, but focuses only on the size of the number involved in the relationships between the two unknown numbers. Expressions such as ''a difference of ...'' may be used.

A Directed (no magnitude) relationship recognises which unknown must be larger or smaller - naming Box A and Box B or c and d - but stops short of expressing the magnitude of the relationship. It may not refer to the operation involved.

A Directed (non-referenced) Relationship identifies the number and operation that are needed for an equivalent expression, but fails to include a reference to Box A and Box B, or to c and d.

A (Fully) Referenced Directed Relationship correctly identifies the condition that is needed for equivalence, specifying the magnitude and direction of the operation involved, with clear reference to Box A and Box B, or to c and d.

Specific values only for c and d are given which make the sentence correct. Almost without exception, only one pair is given without describing the mathematical relationship between c and d.

4.3. Examples of fully relational responses to Question2(Subtraction):

Several São Paulo students did demonstrate clear relational thinking for Type II and Type III addition sentences. In their responses to the Type II Subtraction sentence (shown below), they were able to specify the relationship between the numbers in Box A and the numbers in Box B with clear references to the numbers, including the magnitude and direction of the difference between them. Here we show the responses of two of these students, Rafaella and Flavia, in their answers to the above Type II and Type III Addition questions:

4.3.1. Student A (Rafaella):

''Every number in the Box B has two units less than Box A, for this (reason) it can be the same result'' (part b);

''The Box A will have to be 5 units bigger than Box B'' (part c);

''Yes, if the Box A will have two more units than the Box B'' (part d);

''That 'c' and 'd' has the difference from 8 numbers, because like this, both numbers will have the same result'' (part e) [actually a non-directed relational response].

''In this case, the numbers in the Box A has to be three units lower than Box B'' (see 4.6 below);

4.3.2. StudentB (Flavia):

''Every number in the Box B has two units lower than Box A, so it can give you the same result'' (part b);

''The box A would have more than five units to the box B'' (part c); ''Yes, if the Box A would have two more units than the Box B'' (part d);

The student did: .... The difference between c and d is from eight numbers.'' (part e)

From these clear relational responses by Rafaella and Flavia with regard to Type II sentences, we note that they gave a correct response to Type III sentences only in the case of Addition. No student in the São Paulo sample was able to give a fully referenced and directed response to part e (Type III) for multiplication (see 4.7 below). Furthermore, Type II and Type III division questions could not be answered successfully by any student (see 4.8 below). Because of the limited size of the sample, we cannot generalize based on these results. Other students in other schools may be more successful in dealing with these questions than those in our sample. However, what we are able to say is that responses from the majority of students fell into categories of incorrect or incomplete relational thinking. We therefore need to look at these responses and to see what they tell us about students' attempts to think relationally, and what implications for teaching might be drawn from these responses. Investigating these issues will comprise the remainder of this paper.

4.4. Examples of Incorrect, Incomplete and Complete Relational Thinking

Apart from a few students who were able to give consistent relational responses across some of the four operations, many other students gave responses that were less consistent. For example, they answered part b and part c components more or less relationally, but were unable to show in part d how any number could be used in Box A and still have a true statement. Very few students were able to give a complete answer to any Type III sentence asking them to discuss the values of c and d which made the sentence true. Other students gave incorrect answers. The prevalence of incomplete and incorrect justifications therefore prompts us to look closely at these responses and to draw some important conclusions about the development of relational thinking and how it can be assisted. A wide selection of responses for all four operations are shown in the following section.

4.5. Examples of Justifications for Type II and Type III Addition sentences

Non-Relational: ''I just need to put the right number in the Box B to have the same result in both of counts''; ''Yes. If the number in the Box B makes the same result. In the Box A, I can put any number, but in the Box B no. To put the number in Box BI would need (do) a count.''

Incorrect Relationship: ''No, because the Box A always will be bigger than Box B. If we put ''1'' in the Box A, for example, it will be impossible make equal A and B'';

Non-directed Relationship: The difference between c and d is eight numbers'' or ''c and d has the difference from eight numbers, because that both of them will make the same result''

Directed (no magnitude):''The number in the Box A would be bigger than the number in the Box B''; ''The 'c' will be bigger than 'd''';

Directed (non-referenced) Relationship: ''The relation between has been 5 numbers less'';

Referenced Directed Relationship: ''Every number in the Box B has two units less than the number in Box A'' or ''The Box A always will be two numbers more than Box B '' or ''The number in the Box A has two units more than the number in the Box A''''''The Box A has to have five units more than Box B'' or ''The relation still continuous the same, only change is that in Box A should be 5 more than Box B''; ''Yes, if the Box A will have two more units than the Box B''; ''(12 + 2) = (4 +10) .... The difference between c and d is from eight numbers''

Specific values for c and d: ''I can say that c is 9 and d is 1''; ''I can say that c is 10 and d is 2''.

4.6. Examples of Justifications for Type II and Type III Subtraction sentences

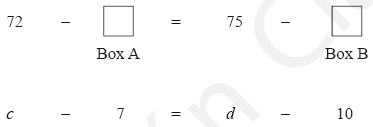
Non-Relational: ''The relation is that the numbers are different'' ;''I can put any number in the Box A, I just need to put the right number in the Box B to have the same result in both of counts''; ''No, because if the Box B will be lower that Box A, the count will be wrong.''

Incorrect Relationship: ''No, because the Box A could never have a negative number''; ''The number in Box A is bigger than the number in Box B ''; ''I can say that 'c' is always 3 number bigger than 'd''';

Non-directed Relationship: ''Yes, because it is possible to put any number in the Box A and then, later, I take off the difference in the Box B''; ''The difference between 'c' and ' d' is three numbers''

Directed (no magnitude): ''Always you put any number in the Box A, you will have to put the difference in the Box B ''; ''The relation will be the number in the Box B always will be bigger than the number in the Box A ''; ''The 'd' will be bigger than 'c''';

Directed (non-referenced) Relationship: ''The relation will be 5 more'' (part c); ''The difference is 3.''

Referenced Directed Relationship: ''The Box A is always 3 numbers less than Box B''; ''The Box A has to have five units less than Box B'' (part c); or ''The relation still continues to be the same, only change is that in Box A should be 5 less than Box B '' (part c); ''Yes, if the Box A will have three less units than the Box B''

Specific values for c and d: ''I can say that c is 2 andd is 5''; ''I can say that c is 7 and d is 10 ''.

4.7. Examples of Justifications for Type II and Type III Multiplication sentences

Non-Relational: ''We can say that 'c' and 'd' are in the sentence to replace numbers.''

Incorrect Relationship: ''Only odd numbers in the Box A can do correctly the count''; ''No, because 'A' always will be bigger than 'B'.''

Non-directed Relationship: ''The numbers are different''

Directed (no magnitude): ''The Box B always will have less than the Box A'' or ''The number in Box A is bigger than the other one'';

Directed (non-referenced) Relationship: No example in this question

Referenced Directed Relationship: ''Every number in Box B is equal the half to the number in Box A'' or ''The Box A is the double of the numbers in the Box B'' or ''The relation from Box A is the double to Box B''; ''Yes, if all number in Box A has been divided by 2, it is the result of Box B''(part d)''The relation is that Box A is the triple of the Box B'' or ''Every number in Box A is the triple of the Box B'' (part c);

Specific values for c and d: ''The letter 'c' is 7 and the letter 'd' is 1''; ''The letter 'c' is 14 and the letter 'd' is 2''.

4.8. Examples of Justifications for Type II and Type III Division sentences

Non-Relational: ''The relation is that the result is different''; ''No, because there is only one way to make the sentence''or ''Yes, it is only to put the correct number in the Box B'' or ''Yes, it depends on the number''; ''The letters 'c' and 'd' are replacing the absent numbers'' or ''The letters 'c' and 'd' are equivalent to two numbers.''

Incorrect Relationship: No example in this question

Non-directed Relationship: No example in this question

Directed (no magnitude): ''The Box A has less than the Box B'';

Directed (non-referenced) Relationship: No example in this question

Referenced Directed Relationship: No example in this question

Specific values for c and d: ''I can say 'c' is 4 and 'd' is 12''.

5. LEARNING FROM THESE INCOMPLETE OR INADEQUATE JUSTIFICATIONS

Responses from students who have been unable to grasp the main point of the question by saying that the sentence will be true if one puts ''the right numbers'' in Box A and Box B have been classified as Non-Relational. Sometimes students refer to the need to have ''different numbers'' in Box A and Box B, or for c and d. While these justifications may be inadequate, they do show that students appreciate the need for equivalence to be satisfied by having ''the right numbers'', even if they are unable to specify how the ''right numbers'' are related.

Some of the Incorrect relationships shown above are evidence that students are sometimes confused about the allowable domain for the numbers in Box A and Box B. In the response to 2d for the Addition sentence, the student thinks that it is impossible for the number in Box A to be 1, '' ...If we put ''1'' in the Box A, for example, it will be impossible make equal A and B''. That conclusion holds only if Box A and Box B are only allowed to contain positive whole numbers. Teaching is needed in order to show how the domain of possible numbers for Box A and Box B can include negative numbers. This will be particularly important in junior secondary school years. A similar problem seems to arise for the student who answers part d for the Subtraction sentence by saying that ''No, because the Box A could never have a negative number.'' The first Incorrect response for multiplication is also curious because the student believes that ''Only odd numbers in Box A make the sentence correct''. A more common response from students - as shown in responses from the other countries - is to argue that Box A has to be an even number for the relationship to be true for multiplication. Of course, if Box A has an odd number in it, then the number in Box B cannot be a whole number. Teachers need to show students how odd numbers, fractional, and decimal values can be used in Box A and Box B even if it is highly likely that students will use relatively simple whole numbers to write three correct instances of the relevant number sentence in 2a, 4a, 6a, and 8a.

In the case of division, some students - not in this sample - correctly point out that the numbers in Box A and Box B have to exclude zero. However, this observation aside, the uncertainties expressed in these incorrect justifications point to an important step that needs to be taught in order to show students the extent of the allowable domain of variation for the numbers in Box A and Box B.

Non-directed relationships take a different form when students simply refer to the difference between the numbers in Box A and Box B, or between c and d. This was most evident in responses to part e questions for Addition and Subtraction, where students correctly draw attention to the difference between c and d [8 in the case of addition and 3 in the case of subtraction] without saying which is larger or smaller. In responses from students in other countries, it is relatively common for students to answer question 2b (Addition) by saying ''Difference of 2'', or to question 4b (subtraction) by saying ''Difference of 3''. This form of incomplete justification may be a carry-over from the way students have been accustomed to talk about relationships between counting numbers. Given two numbers, such as 18 and 20, or 72 and 75, it is permissible to talk about a difference of 2 or 3 as the case may be, because it is clear what two numbers are being referred to, and which one is greater. Of course, it is also correct to say that 18 is two less than 20, or that 20 is two more than 18 - with similar statements describing the relationships between 72 and 75. However, when dealing with Box A and Box B number sentences, and with sentences involving c and d, students may not be aware that only the latter type of sentences can be used, because they are the only ones that make it clear which (variable) numbers are being referred to and which is greater.

A similar problem appears to arise in the case of Directed (non-referenced) relationships. While these kinds of justifications draw attention to the size -magnitude and direction - of the relationship between the unknown numbers, the justification is incomplete because Box A and Box B, or c and d, are unreferenced. Again, this may be a carry-over from the way in which students talk about whole (and rational) numbers. In these latter cases, it can be argued that referring to the difference between two numbers is perfectly clear when one knows the two numbers under discussion. However, when discussing the values of Box A and Box B, or c and d, students need to know that these entities do not have known values, and for that reason, it is always necessary to refer explicitly to them. They must always be named.

Directed (no magnitude) relationships are incomplete, even though students are able to correctly identify the number which has to be bigger or smaller. They are incomplete because students do not specify the magnitude or size of the relationship. We should also be careful not to infer from this kind of incomplete justification that students understand that the numbers in questions are variable numbers. They may have in mind only specific values for the unknown numbers.

Of course, these problems are overcome in the case of Directed and referenced relationships. However, while these justifications appear to be complete, even they need to be examined further in a class discussion where key elements such as allowable domain can be discussed.

Specific values of c and d are a form of incomplete justification peculiar to questions 2e, 4e, 6e and 8e. In the case of all Box A and Box B questions, students are invited to give three correct examples of the relationship, and in this regard, most students were able to write three examples, although a minority of students sometimes simply repeated the one correct instance three times. The fact that students typically gave only one pair of correct values for c and d does raise a serious question of whether students appreciate that c and d are variable numbers. Even more disconcerting is the fact that students appeared not to recognise to mathematical similarity between the four sentences involving c and d and their corresponding Box A and Box B sentences. Both these issues are probably best addressed through a class discussion where the teacher can collate several different responses to the same question involving c and d. This allows students to understand that, while they may have given a single pair of values for c and d, there are in fact multiple pairs of solutions; and hence the need to seek a rule that can encompass the variety of possible solutions. In the case of the 6e multiplication question, the given values for (c, d) are given as (7, 1) and (14, 2) as shown. This pair of possible solutions could be extended through class discussion to include (28, 4), (70, 10) and other whole number solutions. It should also be extended to include decimal and fractional values such as (0.7, 0.1) and (3½, ½), even though these are less likely to be used by students if left to themselves. With the range of solutions so extended, and where the domain is made to include negative numbers as well as whole numbers and rational numbers, students are better placed to see that the list of possible solutions can be extended without ever coming to an end. Hence, the need for some general rule that will allow them to cover not only the possible solutions listed by the class but all other possible values.

6. FINDINGS AND CONNECTIONS FROM SEVERAL COUNTRIES

In implementations of the same research questions consisting of the same Type II and Type III questions in Australia (Stephens, 2007, 2008), in China (Stephens & Wang, 2008), and in Indonesia (Stephens & Armanto, 2010), two conclusions strongly support the findings of this exploratory study of students' relational thinking in Brazil. Firstly, these other studies show the same uses of incomplete justifications that tend to confirm the categorizations used in this paper. This is especially interesting since these different forms of incomplete relational thinking appear to be independent of the particular language used - whether it is Portuguese, Mandarin Chinese, Bahasa Indonesian, or English. The prevalence ofthese various forms of incomplete relational thinking shows that many students of roughly the same age and school mathematical experience continue to experience difficulty in expressing themselves in clearly relational terms and so cannot frame a generalisation to describe how the given numbers vary (see Fujii, 2003; Cooper & Warren, 2011). We are not implying that the results of the sample used in this exploratory study are mirrored exactly in the other studies. The other studies sometimes showed that more students at the same Year level were able to engage in sophisticated relational thinking. Moreover, there may be other schools in Brazil where some students are more confident in relational thinking. The point we can make with confidence is that relational thinking needs to be cultivated, and that the various forms of incomplete relational thinking and non-relational thinking documented here are common across all the other studies. Non-relational and incomplete relational thinking needs to be supported by more explicit teaching in order to assist students in making progress and to remedy these prevalent incomplete forms.

Do students' responses to particular sub-questions predict the likelihood of their success or lack of success on subsequent sub-questions? The answer is that, across these countries, students' responses to part b and c of Type II questions demonstrate different potentials for successfully completing parts d and e of Type II and Type III questions. If students cannot completely specify the relationship between numbers in Box A and Box B in parts b and c, they cannot describe (in part d) how any number might be used in Box A and still have a true sentence. It is nearly impossible for students to answer a part d problem correctly if they have given an incomplete or incorrect justification to parts b and c. Students' correct answers on part b and c make it likely that they will be able to provide a correct answer for part d, and this is true for all four operations:

On the other hand, a successful generalisation in relation to Type II number sentences in part d is usually followed by a successful explanation of the relationship between c and d in Type III sentences. Successful performances on Type II and Type III sentences appear to be closely related. For example, one student commented that c and d ''are just like Box A and Box B''. When part d is correct, it is usually followed by a correct response to part e. This is illustrated as follows:

On the other hand, students who were unable to specify in fully relational terms the relationship between the numbers in Box A and Box B in parts b and c for Type II sentences, were always unable to specify the relationship between c and d in Type III sentences (part e). Having a correct answer for part b and c appears to be necessary condition for answering part e correctly:

On the other hand, some students who successfully described the relationships between c and d in part e, and having given a complete relational description to parts b and c, were not able to describe how any number could be used in Box A and still have a true number sentence. This suggests that framing a generalisation in part d may be more difficult for some students than generalising the relationship between c and d.

7. CONCLUSIONS AND IMPLICATIONS FOR TEACHING

In this exploratory study from a sample of Brazil students, very few students used relational justifications in solving Type I number sentences. The majority of correct answers to Type I number sentences seemed to be achieved using calculation. This clear reliance on calculation to solve Type I number sentences led to the need for a different kind of number sentence - namely Type II and Type III sentences - where students could no longer rely on calculation to achieve a successful result. Among the justifications offered by students for these sentences there was clear evidence of relational thinking, but it was still at a developing stage. We characterized several distinct kinds of incomplete relational thinking, and a small number of responses were categorized as non-relational or pre-relational. The sample size used in this study is small and does not justify us allocating proportions to these categories. However, the prevalence of responses conforming to the various categories is consistent with similar studies carried out in other countries. What implications for teaching arise from these incomplete responses?

While these limited relationships denote an early stage of relational thinking development, how can teachers use these limited relationships to support their students so that they are able to understand the need for and to express referenced and directed relational descriptions? This may be carried out by highlighting to students the disadvantages and advantages that different descriptions offer. When, for example, students say: ''There is two difference'' or ''Box A and Box B differ by two'' (as in the case of the addition question above), teachers should ask students to consider whether the expression 'Two difference' is completely clear to them. Teachers need to encourage students to say: ''Do we know which one is bigger?'', '''Two difference' doesn't tell us'', or: ''It's like saying that there is a difference of 10 centimetres between my height and the height of my friend. That doesn't tell us which one is taller''. In this way, teachers can help students think about whether these partial descriptions, typical of incomplete relational thinking, tell them what they need to know; and if they do not, how these descriptions can be improved?

Similarly, in Type III sentences, students need to know that specific values for c and d, while correct, are not the only possible answers. Teachers should ask students if they can find other correct pairs of c and d that make the Type III sentence correct. At first, it is very likely that students will suggest different whole number values for c and d. That may be enough for students to see a pattern. However, teachers need to ask students to consider if c and d might have fractional or decimal values. (Later, it might be possible to ask if c and d could be negative, and satisfy, for example, c + 2 = d + 10). This kind of discussion helps students to think of c and d as variable numbers that can take many possible values, provided c is 8 more than d.

Finally, we need to make several general recommendations to assist teachers in using the potential of Type I, II, and III sentences. Working with and discussing these several varieties of number sentences in the classroom can show teachers where students typically find these number sentences difficult to understand and solve. For example, knowing that many students will solve Type I sentences computationally and correctly, teachers need to encourage students to think about other ways of solving Type I sentences. In the case of Type II sentences, they will know that many students need help to correctly and fully express the relationship between Box A and Box B. In the case of Type III sentences, teachers also need to know that many students are inclined to stop after giving a specific pair of values for c and d that satisfy these sentences. Using the kind of classroom explorations that we have advocated above, teachers can help students to appreciate the mathematical similarities between Type II and Type III sentences and, as a result, build a clearer appreciation of how the numbers in Box A and Box B can be viewed as prototypes for c and d. These ''generalizations of the arithmetic model'', as we have seen, depend on having an in-depth understanding of equivalence and compensation; attention to structure and operations; attending to the range of possible variation (which numbers vary, which numbers stay the same); and generalisation. Relying on Type I number sentences alone to achieve these goals is probably insufficient. Strategies, such as teaching with variation, can help students to see that, for both Type II and III sentences, the permissible range of variation can include rational numbers and negative numbers. This can help to build a stronger foundation for the subsequent idea of variable in high school mathematics. These are clear examples of and necessary steps to achieving what Brazil's national curriculum standards means by ''working towards algebra''.

ACKNOWLEDGMENTS

We would like to thank Marcio Dorigo and Yuri Osti Barbosa, who assisted with data collection.

REFERENCES

ACARA, Australian Curriculum and Reporting Authority (2010). The Australian Curriculum: Mathematics. Sydney, Australia: ACARA. [ Links ]

Britt, M. & Irwin, K. (2011). Algebraic thinking with and without algebraic representation: A pathway for learning. In J. Cai & E. Knuth (Eds.), Early Algebraization: A global dialogue from multiple perspectives (pp. 137-159). Heidelberg, Germany: Springer. DOI: 10.1007/9783-642-17735-4 [ Links ]

Cai, J., Ng, S. & Moyer, J. C. (2011). Developing students' algebraic thinking in earlier grades: Lessons from China and Singapore. In J. Cai & E. Knuth (Eds.), Early Algebraization: A global dialogue from multiple perspectives (pp. 25-41). Heidelberg, Germany: Springer. DOI: 10.1007/978-3-642-17735-4_3 [ Links ]

Carpenter, T. P. & Franke, M. L. (2001). Developing algebraic reasoning in the elementary school: Generalization and proof. In H. Chick, K. Stacey, J. Vincent & J. Vincent (Eds.), Proceedings of the 12^th ICMI Study Conference: The Future of the Teaching and Learning of Algebra (Vol. 1, pp. 155-162). Melbourne, Australia: University of Melbourne. [ Links ]

Carpenter, T. & Levi, L. (1999). Developing conceptions of algebraic reasoning in the primary grades. Paper presented at the Annual Meeting of the American Educational Research Association, Montreal, Canada. [ Links ]

Cooper, T. & Warren, E. (2011). Year 2 to Year 6 students' ability to generalize: Models, representations and theory for teaching and learning. In J. Cai & E. Knuth (Eds.), Early Algebraization: A global dialogue from multiple perspectives (pp. 187-214). Heidelberg, Germany: Springer. DOI: 10.1007/978-3-642-17735-4_12 [ Links ]

Fujii, T. (2003). Probing students' understanding of variables through cognitive conflict problems: Is the concept of a variable so difficult for students to understand? In N. A. Pateman, B. J. Dougherty & J. Zilliox (Eds.), Proceedings of the 27^th Conference of the International Group for the Psychology of Mathematics Education (Vol. 1, pp. 49-65) Hawaii, U.S.A.: University of Hawaii. [ Links ]

Fujii, T. & Stephens, M. (2001). Fostering understanding of algebraic generalisation through numerical expressions: The role of quasi-variables. In H. Chick, K. Stacey, J. Vincent & J. Vincent (Eds.), Proceedings of the 12^th ICMI Study Conference: The Future of the teaching and learning of algebra (Vol. 1, pp. 258-264). Melbourne, Australia: University of Melbourne. [ Links ]

Hart, K. M. (1981). Children's understanding of Mathematics: 11-16. London, England: John Murray. [ Links ]

Irwin, K. & Britt, M. (2005). The algebraic nature of students' numerical manipulation in the New Zealand Numeracy Project. Educational Studies in Mathematics 58(2), 169-188. [ Links ]

Jacobs, V., Franke, M., Carpenter, T., Levi, L. & Battey, D. (2007). Professional developing focused on children's algebraic reasoning in elementary School. Journal for Research in Mathematics Education 38(3), 258-288. [ Links ]

Katz, V.J. (Ed.). (2007). Algebra: Gateway to Technological Future. Washington, DC: The Mathematical Association of America. [ Links ]

Kaput, J., Carraher, D. & Blanton, M. (Eds.) (2008). Algebra in the early years. Hillsdale, NJ, U.S.A.: Lawrence Erlbaum Associates and National Council of Teachers of Mathematics. [ Links ]

Kieran, C. (1981). Concepts associated with the equality symbol. Educational Studies in Mathematics 12(3), 317-326. [ Links ]

Lins, R., & Kaput, J. (2004). The early development of algebraic reasoning: The current state of the field. In K. Stacey, H. Chick, & M. Kendal (Eds.), The Future of the teaching and learning of algebra: The 12^th ICMI Study, (pp.47-70). Boston, U.S.A.: Kluwer Academic Publishers. DOI: 10.1007/1-4020-8131-6_4 [ Links ]

Mason, J., Stephens, M., & Watson, A. (2009). Appreciating mathematical structure for all. Mathematics Education Research Journal 21(2), 10-32. DOI: 10.1007/BF03217543 [ Links ]

Ministerio da Educaçao Brasil (1998). Parámetros Curriculares Nacionais. Brasilia: MEC/SEF. Recuperado el dia 15 de Marzo de 2004: de http://www.mec.gov.br/sef/sef/pcn.shtm. [ Links ]

Ministerio da Educaçao Brasil (2000). Parámetros Curriculares Nacionais: ensinomedio Brasilia: MEC/SEMTEC. Recuperado el dia 10 de Septiembre de 2009 de: http://portal.mec.gov.br/seb/arquivos/pdf/ciencian.pdf [ Links ]

Ministry of Education of People's Republic of China (2001). Mathematics Curriculum Standards for Compulsory Education. Beijing, China: Beijing Normal University Press. [ Links ]

Ministry of Education of People's Republic of China (2011). Mathematics Curriculum Standards for Compulsory Education (2011 version). Beijing, China: Beijing Normal University Press. [ Links ]

Molina, M., Castro E. & Ambrose, R. (2006). Trabajo con igualdades numéricas para promover pensamiento relacional. PNA 1(1), 31-46. [ Links ]

Molina, M., Castro, E. & Mason, J. (2008). Elementary school students' approaches to solving true/false number sentences. PNA 2 (2), 75-86. [ Links ]

NCTM, National Council of Teachers of Mathematics (2006). Curriculum Focal Points for Prekindergarten through Grade 8 Mathematics: A Quest for Coherence. Reston, VA, U.S.A.: NCTM. [ Links ]

Skemp, R. (1976). Relational understanding and instrumental understanding. Mathematics Teaching 77, 20-26 [ Links ]

Stephens, M. (2007). Students' emerging algebraic thinking in the middle school years. In J. Watson & K. Beswick (Eds.), Proceedings of the 30^th Annual Conference of the Mathematics Education Research Group of Australasia: Mathematics: Essential Research, Essential Practice (Vol. 2, pp. 678-687). Hobart, Australia: MERGA. [ Links ]

Stephens, M. (2008). Some key junctures in relational thinking. In M. Goss, R. Brown & K. Makar (Eds.), Proceedings of the 31^st annual conference of the Mathematics Education Group of Australasia: Navigating current and charting directions (Vol. 2, pp. 491-498). Brisbane, Australia: MERGA. [ Links ]

Stephens, M., & Armanto, D. (2010)., How to Build Powerful Learning Trajectories for Relational Thinking in the Primary School Years. In L. Sparrow, B. Kissane & C. Hurst (Eds.), Proceedings of the 33^rd Annual Conference of the Mathematical Education Research Group of Australasia: Shaping the Future of Mathematics Education (Vol. 2, pp. 523-530). Fremantle, Australia, MERGA. [ Links ]

Stephens, M., & Wang, X. (2008). Investigating Some Junctures in Relational Thinking: A study of Year 6 and Year 7 Students from Australia and China. Journal of Mathematics Education 1 (1), 28-39. [ Links ]

Stephens, M., & Wang, X. (2009). Probing some key junctures in relational thinking: A study of Year 6 and Year 7 students from Australia and China. In R. Hunter, B. Bricknell & T. Burgess (Eds.), Proceeding of the 32^nd Annual Conference of the Mathematics Education Group of Australasia: Crossing Divides (Vol. 2, pp. 499-506). Wellington, New Zealand: MERGA. [ Links ]