Introducción
Los retardos han estado presentes en diferentes tipos de sistemas de diversas áreas, por ejemplo, sistemas y modelos sociales, tecnológicos, electrónicos, de comunicaciones, biológicos, biomédicos, robóticos, mecatrónicos, entre otros; causando inestabilidad, oscilaciones y efectos de ruido. Dicho fenómeno aparece en la entrada y salida durante el envío y la recepción de señales del sistema, de la energía o del procesamiento de información, provocando deterioros de los sistemas. Actualmente existen teorías del control enfocadas específicamente para los sistemas con retardos, donde el sistema contiene por naturaleza retardos como: sistemas de combustión, sistemas eléctricos, sistemas de comunicaciones, entre otros (Fridman, 2014; Gu et al., 2003; Niculescu, 2001). Sin embargo, hay contribuciones de sistemas con retardos desde el diseño de controladores que contribuyen directamente en la estabilidad de la planta (Ramírez et al., 2015b; Gu et al., 2005; Cooke et al., 1982; Ramírez et al., 2015a; Ramírez et al., 2017). Dichas aportaciones han contribuido dentro de la línea de investigación para el control de sistemas con retardos, cuya implementación y diseño de los controladores con retardo han resuelto problemas donde están presentes ruidos, perturbaciones y oscilaciones, evitando en muchos casos, la medición de variables y haciendo uso de los filtros (Ramírez et al., 2017; Villafuerte et al., 2010; Villafuerte et al., 2012). Actualmente en la literatura existen dos enfoques de los sistemas con retardos para el estudio, el análisis de estabilidad y el diseño de controladores que engloban el enfoque frecuencial y temporal (Gu et al., 2005; Bellman et al., 1963; Cooke et al., 1994; Louisell, 1998; Krasovskii, 1956; La Salle et al., 2012; Razumikhin, 1956; Zubov, 1961).
Este trabajo está enfocado en el análisis frecuencial mediante el uso de cuasipolinomios. Dicho enfoque está basado en garantizar la estabilidad del sistema con retardos en el dominio complejo mediante el lugar de las raíces, realizando el análisis en lazo cerrado. El objetivo del enfoque frecuencial es colocar las raíces del cuasipolinomio en el semiplano izquierdo complejo para lograr que el sistema sea estable, es importante mencionar que si al menos una raíz se encuentra en el semiplano derecho el sistema será inestable (Cook, 1962 y 1966). Por lo tanto, es importante analizar el cruce de las raíces por cero, cuyo estudio ha sido aplicado para el análisis y el diseño de controladores de sistemas inestables, no lineales y oscilatorios con retardos.
Un estudio particular ha sido con el controlador Posicast para implementar un controlador capaz de amortiguar las oscilaciones con un retardo aplicado a un sistema de segundo orden lineal subamortiguado; donde el fin es amortiguar el fenómeno oscilatorio presente en esta clase de sistemas, cuando el coeficiente de amortiguamiento es menor a uno (Hung, 2003 y 2007) con infinito número de ceros estables. En Hung (2003) se modela un servomecanismo usando un patrón de segundo orden para la propuesta de un compensador Posicast incluyendo su estabilidad. En general, se ha probado que el controlador Posicast es capaz de estabilizar sistemas de segundo orden subamortiguados. En Hung (2007) se estudia un controlador integral (I) con estructura en cascada, se analiza el sistema mediante análisis frecuenciales.
Por otro lado, en Vrancic et al. (2012) se analiza y presenta el controlador Posicast, donde se detalla desde la sintonización hasta ejemplos prácticos, sin embargo, se considera un controlador en lazo abierto. Finalmente, también es propuesto un método de diseño para un controlador Proporcional Integral Derivativo (PID) en conjunto con un controlador Posicast. No obstante, los métodos de diseño y de sintonización de los controladores presentados en la literatura son mediante métodos iterativos donde los parámetros dependen de momentos característicos del proceso y de los filtros, los cuales pueden variar o tener diferentes aproximaciones según sea el caso.
Cabe mencionar que en este artículo se presenta un controlador Proporcional Integral Posicast para la estabilización de un sistema de segundo orden subamortiguado y es validada su robustez cuando se agrega una perturbación externa y constante en la salida, obteniendo un error en estado estacionario cero. Por lo tanto, la contribución de este artículo es añadir robustez mediante un controlador PI-Posicast capaz de amortiguar las perturbaciones externas con un lazo de control realimentado PI (Proporcional Integral) y el controlador Posicast en cascada.
En suma, el controlador es sintonizado mediante técnicas y metodologías óptimas para la estabilización de sistemas con retardos mediante el máximo decaimiento exponencial (Niculescu, 2001) y el método de D-particiones (Neimark, 1949). Además, se realiza el análisis y la simulación del controlador PI-Posicast que garantiza la robustez ante distintas perturbaciones añadidas al sistema y se comprueba la estabilidad del sistema perturbado mediante condiciones de σ-estabilidad.
Este artículo se organiza con la siguiente estructura: en la sección II se presenta la estructura del controlador Posicast, sus ventajas y sus desventajas. En la sección III se muestra la propuesta del artículo basado en el controlador PI-Posicast, el análisis en el dominio de la frecuencia usando D-particiones y el criterio de σ-estabilidad; y la estabilidad robusta del controlador propuesto. Finalmente en la sección IV se presentan las conclusiones y los trabajos futuros.
Control Posicast
El controlador Posicast fue diseñado por Smith (1957) para una clase de sistema de segundo orden subamortiguado, en la época de los cincuenta. La principal aportación de dicho trabajo fue amortiguar las oscilaciones en este tipo de sistemas. El efecto principal del controlador Posicast de Smith está basada en la asignación de los polos de la función de transferencia del sistema, los cuales son cancelados con los ceros del sistema en lazo cerrado. El controlador Posicast es aplicado para una clase de sistema de segundo orden de la forma:
en términos de los parámetros del coeficiente de amortiguamiento determinado en el rango 0 < ς < 1 y ω n la frecuencia natural. El diagrama de bloques del controlador Posicast propuesto por (Smith, 1957) se presenta en la Figura 1.
Cuya ganancia k ∊ ℝ+ es determinada como:
Donde a se define como el sobreimpulso máximo dado como:
La metodología del diseño del controlador Posicast está basada en separar la señal de referencia en dos secciones. En la primera sección son aplicadas directamente las ganancias. Por otro lado, la segunda acción de control es multiplicada con un retardo en el tiempo definido con T n como el periodo natural:
Donde el retardo h se define como:
El sobreimpulso máximo es representado por a y es mostrado gráficamente en la Figura 2, donde puede ser estimado mediante el periodo natural T n de la respuesta del sistema ante una entrada escalón.
Matemáticamente, el controlador Posicast se define mediante la siguiente función de transferencia:
Por otro lado, representando la Ecuación 6 en diagramas de bloques se obtiene la Figura 3. Donde es posible observar que el controlador Posicast tiene un retardo aplicado en el término a / 1 + a de la señal de referencia en un tiempo t < h. Además, es importante considerar que la salida del sistema es capaz de llegar al valor de referencia en un tiempo t ≥ h y pueda lograr un error en estado estacionario cero (Smith, 1957) como se muestra en la Figura 4.
Obteniendo la respuesta del sistema con y sin el controlador Posicast (Smith, 1957) (Figura 4) puede observarse que la respuesta de salida con el controlador Posicast en cascada es capaz de amortiguar las oscilaciones, incluso es capaz de alcanzar la referencia en menos del periodo de oscilación del sistema (t = 3.2064 seg), en caso contrario, puede verse la presencia de oscilaciones. Comprobando analíticamente la respuesta de la Figura 3 y estimando el error en estado estacionario para el controlador Posicast, además de considerar una referencia constante cuya función de transferencia del sistema es definida como:
Donde la salida es:
Además, la referencia es considerada constante. Por ende, su transformada de Laplace es:
Aplicando para estimar la salida el teorema del valor final (Spiegel, 1965) se emplea la referencia, el sistema y el controlador Posicast y se tiene:
Así, la salida del sistema en estado estacionario llega a la referencia deseada como se muestra en la Figura 4.
Sin embargo, ahora se pone a prueba de robustez el controlador Posicast, por lo que se agrega una perturbación externa y constante como se muestra en el diagrama de la Figura 5. Obteniendo la respuesta en el tiempo (Figura 6), puede observarse que la salida del sistema no converge a la referencia. Por tanto, existe un error en estado estacionario y se concluye que el controlador Posicast no es robusto.
Para demostrar analíticamente lo anterior, se considera el caso de insertar una perturbación externa y constante como se ve en el diagrama de la Figura 5. Del diagrama de bloques de dicha figura pueden definirse las siguientes funciones de transferencia:
y
Lo que ayuda a determinar la salida del sistema:
Por otro lado, la transformada de la Laplace de la perturbación constante se define como:
Ahora, aplicando el teorema del valor final para el sistema perturbado se estima la salida como:
Analíticamente se puede concluir que el efecto de la perturbación externa y constante aplicada al sistema provoca que la salida no sea la referencia, sino aún más, aparezca el efecto de la perturbación.
Por lo tanto, se recurrió a la propuesta de solución de este artículo, la cual ayudará a contrarrestar el efecto de la perturbación, es decir, se añade robustez mediante la suma del controlador PI (Proporcional Integral) en conjunto con el controlador Posicast en cascada.
El diseño del controlador PI-Posicast robusto se realiza mediante el uso de técnicas de implementación y estabilidad, empleadas para los sistemas con retardos (Fridman, 2014; Gu et al., 2003; Niculescu, 2001; Bellman et al., 1963; Cooke et al., 1994; Smith, 1957) el cual se presenta a continuación.
Controlador PI-Posicast
El controlador PI-Posicast, en cascada para el sistema de segundo orden tiene como objetivo amortiguar los efectos de las perturbaciones insertadas al sistema. Para el diseño del PI-Posicast robusto se utilizaron el sistema de segundo orden subamortiguado con el parámetro en el rango 0 < δ < 1 y el controlador Posicast de Smith, presentado anteriormente. Por lo tanto, ahora se valida cómo el PI-Posicast, en contraste al Posicast, tiene la ventaja de ser robusto, es decir, es capaz de amortiguar las perturbaciones externas y constantes insertadas al sistema.
El controlador PI-Posicast se define de la siguiente forma:
Donde puede observarse el control PI en conjunto con el controlador Posicast, cuyo diagrama de bloques se ejemplifica en la Figura 7.
A continuación, se presenta el diseño del controlador mediante el uso del control basado en retardos, empleando el análisis en el dominio de la frecuencia y usando D-Particiones y el criterio de σ-estabilidad.
Análisis en el dominio de la frecuencia
Para este análisis es necesario aplicar las técnicas de los diagramas de bloques, por lo que, obteniendo la función de transferencia del diagrama de bloques de la Figura 7 se tiene:
Donde el cuasipolinomio característico en lazo cerrado es determinado por:
Ahora se aplica el método D-particiones (Neimark, 1949) para determinar las regiones de parámetros del controlador y estimar los cruces de estabilidad/inestabilidad. Para ello, es necesario sustituir s = 0 y s = iω en la Ecuación 18 para determinar los parámetros k p y k i que garantizan que el sistema sea estable en lazo cerrado.
Para el caso cuando s = 0, se sustituye en la Ecuación 18 y se iguala a cero, es decir:
y despejando k i de la Ecuación 19 se tiene:
De esta manera se puede concluir que el espacio de parámetros está delimitado por la recta en cero para el eje k i y de acuerdo con el método de D-particiones, esto indica el lugar donde los polos cruzan de regiones estables a inestables.
Para el caso s = iω se sustituye en la Ecuación 18 y se iguala a cero, de esa forma se tiene que e -sh = cos hω + i sin hω. Ahora, expandiendo los términos y separando la parte real e imaginaria, e igualando cada parte a cero se tiene:
Despejando de ambas ecuaciones a las ganancias k p y k i , se obtienen las siguientes ecuaciones paramétricas para el espacio de parámetros (k p , k i ).
El espacio de parámetros debe ser seleccionado de manera que al estudiar las regiones de estabilidad sea posible determinar los valores de sintonización para k p y k i y obtenidos mediante el método de D-particiones que garanticen que el sistema en lazo cerrado sea estable, es decir, graficando el espacio de parámetros se determina mediante las Ecuaciones 20, 23 y 24 (Figura 8).
Aunado a lo anterior, los parámetros empleados del sistema para el diseño del controlador Posicast son ς = 0.2, ω n = 1, con un retardo h = 3.2064 y una ganancia k = 0.6924 que logran amortiguar las perturbaciones.
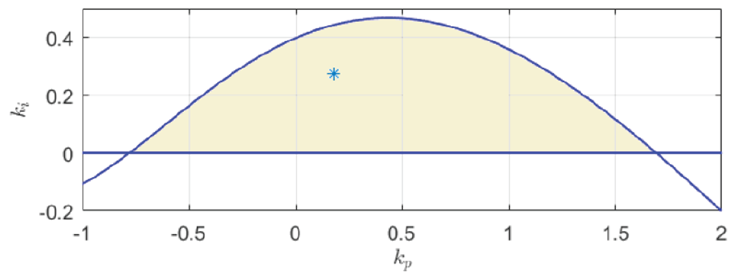
El espacio de parámetros mostrado en la Figura 8 contiene una gran región inestable, a excepción de una región pequeña cerca del origen entre la recta k i = 0 y las curvas de las ecuaciones paramétricas (Figura 9).
La región marcada en la Figura 9 pertenece a las ganancias (k p , k i ) que permiten lograr que el controlador PI-Posicast sea estable en lazo cerrado. Es decir, para que el sistema sea estable basta con seleccionar a las ganancias k p y k i en esta región.
Sin embargo, existen múltiples opciones. Por lo tanto, recurrimos al análisis de σ - estabilidad que determina un valor único de ganancias capaces de estabilizar al sistema y bridar un máximo decaimiento exponencial, como se presenta a continuación.
Análisis de σ - estabilización
El análisis de σ - estabilidad busca garantizar que los parámetros (k p , k i ), que σ - estabilizan al sistema, satisfagan la siguiente ecuación característica:
Lo que implica la existencia de una cota de decaimiento exponencial σ con L > 0.
Considerando la Figura 9, se muestra el espacio de parámetros que garantizan que el sistema de segundo orden bajo el controlador PI-Posicast es estable, ya que es evidente que hay un gran conjunto de ganancias (k p , k i ) que logran este fin. Ello, debido a que el comportamiento de las raíces del cuasipolinomio de la Ecuación 18 en el plano semicomplejo es contínuo respecto a los cambios de los coeficientes y de los tiempos de retardo.
El criterio de σ - estabilidad pierde efectividad cuando las raíces del cuasipolinomio tiene un par de raíces puramente imaginarias y las raíces cruzan el eje imaginario, que en efecto representan a un sistema críticamente estable o inestable mediante sus regiones de estabilidad cuando s = 0 o cuando las raíces son complejas s = ± iω y las raíces cruzan el eje imaginario.
Por lo tanto, es esencial realizar un cambio de variable en el dominio de la frecuencia s → s - σ en el cuasipolinomio característico en lazo cerrado de la Ecuación 18 donde se tiene:
Para el caso s = 0, se sustituye s = 0 en el cuasipolinomio característico de la Ecuación 26 y se iguala a cero para obtener:
Despejando a k p de la Ecuación 27 se tiene:
La Ecuación 28 define la primera frontera y simboliza el cruce de una raíz de alguna región estable a una región inestable. Cabe mencionar que para seleccionar σ se pueden tener datos con valor mayor a cero.
Para el caso s = iω, se sustituye en la Ecuación 26, separando la parte real y la parte imaginaria e igualando ambas partes a cero:
Se despeja k i de la Ecuación 30:
Por otro lado, se sustituye la Ecuación 31 en la Ecuación 29 y se despeja k p :
Así, para los parámetros 0 < ς < 1, ω n , k, h, σ ∊ ℝ+ dados por las Ecuaciones 29, 30, 31 y 32 definen las fronteras σ-estables del cuasipolinomio en lazo cerrado de la Ecuación 26.
Los parámetros (k
p
, k
i
) determinan el máximo decaimiento exponencial y se calculan analíticamente mediante p
σ
|
s=0
=0,
Obteniendo así mediante el método de D-particiones y σ-estabilidad los valores paramétricos fijos ς = 0.2, ω n = 1 y los valores de diseño del controlador Posicast h = 3.2064 y k = 0.6550 que logran brindar el máximo decaimiento exponencial σ * cuando las ganancias en lazo cerrado para el control son k p = 0.1810 y k i = 0.2742125. Cabe mencionar que el máximo decaimiento exponencial se obtiene cuando σ = 0.062659.
Análisis de robustez
El análisis de robustez del controlador es validado matemáticamente mediante el análisis del teorema del valor final, es decir, estimando la salida del sistema de segundo orden subamortiguado con el controlador PI-Posicast y la inserción de perturbaciones externas y constantes.
Para ello, se emplea el enfoque frecuencial para determinar el efecto de una perturbación externa y constante, como se muestra en el diagrama de bloques de la Figura 11.
La función de transferencia para el diagrama de control PI-Posicast de la Figura 11 se estima mediante:
Donde la salida es:
Usando el teorema del valor final para determinar el valor de la salida obtenida en la Ecuación 34 se tiene:
Ahora, estimando la salida en conjunto con el error en estado estacionario usando el teorema del valor final se tiene:
Desarrollando la Ecuación 36 se tiene:
En conclusión, la salida y(t) en el dominio del tiempo en estado estacionario se estima como:
Así, el error en estado estacionario se define como:
Converge a cero. Por lo tanto, es validada la robustez y la efectividad del controlador PI-Posicast cuando se inserta una perturbación externa y constante al sistema.
Para validar los resultados obtenidos se recurre a simulaciones numéricas con el controlador PI-Posicast agregando cuatro diferentes perturbaciones externas y constantes con el fin de evaluar el desempeño del control diseñado previamente. Las simulaciones numéricas se llevaron a cabo con ayuda de Matlab-Simulink R2018b. Como parte de la configuración de la simulación se utilizó un método numérico de paso fijo, en este caso, el Runge Kutta con tamaño de paso de 0.02 segundos y un tiempo de simulación de 28 segundos.
Los resultados del controlador son presentados bajo diferentes salidas del sistema con distintas perturbaciones. Cabe señalar que la perturbación d se incrementa y produce oscilaciones en la salida transitoria. Sin embargo, la perturbación constante y externa al sistema no afecta en el error en estado estacionario de la salida, ya que este converge asintóticamente a cero con la propuesta del controlador PI-Posicast robusto como se demuestra a nivel analítico y simulación (Figura 12).
Conclusiones
En este trabajo se presentó y se profundizó en el diseño del controlador PI-Posicast robusto garantizando su estabilidad en el dominio frecuencial para un sistema de segundo orden subamortiguado que consta de un controlador Posicast en conjunto con un control PI (Proporcional Integral) en cascada.
Se estudió el diseño del controlador Proporcional Integral Posicast (PI-Posicast) aplicado en cascada a un sistema de segundo orden subamortiguado mediante la sintonización de las ganancias usando el método frecuencial de D-particiones del controlador PI-Posicast encontrándose de forma gráfica valores para las ganancias del controlador (k p , k i ) que generan un decaimiento exponencial máximo.
La sintonía del esquema Posicast se logró de acuerdo con resultados reportados en la literatura. Para la sintonía del lazo de control Proporcional Integral se realiza un estudio en el dominio de la frecuencia utilizando el método de D-particiones y σ-estabilidad.
El estudio de robustez en el dominio de la frecuencia garantizó las cotas que garantizan la estabilidad robusta del sistema de lazo cerrado cuando se perturban los parámetros nominales del sistema de segundo orden subamortiguado.
En el caso del controlador se utilizó el método del dominio de la frecuencia para estudiar la robustez del sistema de lazo cerrado, cuando los parámetros del sistema de segundo orden están sujetos a perturbaciones, de esa manera se validó utilizando el teorema del valor final. Posteriormente, se presentaron resultados efectivos que validan la robustez ante diversas perturbaciones.
Sin embargo, se considera realizar un estudio del controlador en el dominio del tiempo. Finalmente, como trabajo futuro se busca realizar un estudio analítico de σ-estabilización y D-particiones en sistemas con modelos matemáticos de segundo orden subamortiguados donde sea posible aplicar el controlador PI-Posicast, incluso el diseño de los controladores PD-Posicast y PID-Posicast con experimentos en tiempo real, como motores eléctricos, motores piezoeléctricos, sistemas robóticos, sistemas mecánicos y sistemas mecatrónicos, entre otros.











 text new page (beta)
text new page (beta)