Introducción
El término fragilidad estructural se refiere a la probabilidad condicional de la falla de una estructura o componente dado un valor específico de la intensidad de la solicitación. La fragilidad se expresa en función de una variable aleatoria que representa la incertidumbre asociada a la intensidad. Los resultados de un análisis de fragilidad se representan a través de una curva de fragilidad. La curva de fragilidad se puede interpretar como la función de distribución acumulativa de la capacidad de la estructura o componente. Conforme la intensidad aumenta, la curva de fragilidad se aproxima a uno. La fragilidad de una estructura en efecto dependerá de las probabilidades de falla de sus múltiples componentes. Por simplicidad, el presente artículo aborda el problema de la fragilidad estructural de componentes o modos de falla individuales.
El análisis estocástico de la falla de componentes se ha utilizado extensamente en la evaluación probabilista del riesgo estructural desde finales de la década de los setentas, en aplicaciones relacionadas con el diseño de plantas de energía nuclear (Kennedy et al. 1980, 1984). Este tipo de análisis también se ha utilizado ampliamente en ingeniería sísmica para analizar la fragilidad -llamada en ocasiones vulnerabilidad sísmica- (Mayoral et al., 2016), y en geotecnia para determinar la probabilidad de falla de elementos de cimentación y otras obras (Popescu et al., 2005; Wu, 2015). En ingeniería hidráulica, este tipo de análisis se utiliza para evaluar el riesgo de inundación de las poblaciones (Vorogushyng et al., 2010; Apel et al., 2004).
Al analizar la fragilidad estructural de componentes, usualmente se supone a priori una distribución lognormal para la curva de fragilidad y sus parámetros se obtienen posteriormente recurriendo a alguna técnica de estimación estadística, ignorando el tipo de densidades de probabilidad de las variables básicas de diseño. Con base en el teorema del límite central (Papoulis, 1984), se puede mostrar que esta hipótesis a priori solo se cumple cuando la función de estado se da por el producto de un número grande de variables de diseño positivas e independientes. Sin embargo, suponer variables de diseño independientes no es una hipótesis válida en la mayoría de los casos. En otras ocasiones, la fragilidad estructural de componentes se evalúa suponiendo implícitamente que las densidades de probabilidad conjuntas entre cualquier par de variables aleatorias son gaussianas (Altarejos et al., 2015; Vorogushyn et al., 2010). El efecto de las densidades de probabilidad conjunta y marginales de las variables básicas de diseño sobre la fragilidad se ha abordado poco en la literatura (Popescu et al., 2005; Choi et al., 2004). El tipo de curva de fragilidad tendrá consecuencias importantes en la cuantificación del riesgo. Por lo tanto, es necesario conocer el efecto de las densidades de probabilidad de las variables básicas de diseño sobre la fragilidad estructural de componentes respecto a un mecanismo y amenaza específicos.
El uso de densidades marginales no gaussianas se justifica en la práctica de la ingeniería cuando los parámetros presentan un intervalo de variación estrictamente positivo y la información que se conoce del comportamiento de las variables incluye, además de un valor esperado y varianza, un valor mínimo y un valor máximo. En otras ocasiones puede suceder que la probabilidad de que ocurran valores positivos excepcionalmente grandes de la variable sea mayor que la que asocia un modelo gaussiano. Además, los resultados de experimentos de campo o laboratorio pueden mostrar un comportamiento distinto al gaussiano.
Al trabajar con variables aleatorias no gaussianas se presenta, sin embargo, la dificultad de expresar su correlación, porque el coeficiente de correlación lineal de Pearson, que se utiliza tradicionalmente para cuantificar la correlación entre pares de variables aleatorias, depende del tipo de densidad de probabilidad de las variables (Lemhann, 1966). Por ello, algunos autores proporcionan soluciones analíticas para el coeficiente de correlación de Pearson entre variables aleatorias con distintos tipos de densidades de probabilidad (Mood y Graybill, 1974). En este artículo se propone recurrir a medidas de correlación invariantes, como es el caso del coeficiente de correlación de Spearman (Schweizer y Wolf, 1981), para expresar correlación entre variables con distintas densidades de probabilidad. Este coeficiente se determina por las variables aleatorias asociadas a las distribuciones acumulativas, que siempre serán uniformes independientemente del tipo de densidad de probabilidad (Papoulis, 1984). Además, tiene la ventaja de estar relacionado directamente con el coeficiente de correlación de Pearson a través de expresiones sencillas (Gnest y Favre, 2007). Como una primera aproximación, en el presente artículo se considera que las densidades de probabilidad conjuntas entre variables aleatorias son gaussianas; una hipótesis muy razonable en ausencia de información acerca del comportamiento multivariado de las variables de diseño. En este contexto, el coeficiente de correlación de Pearson se puede utilizar para expresar la correlación de las densidades gaussianas conjuntas, a partir del coeficiente de correlación de Spearman, que expresaría la correlación deseada entre las variables marginales no gaussianas.
Conceptos básicos
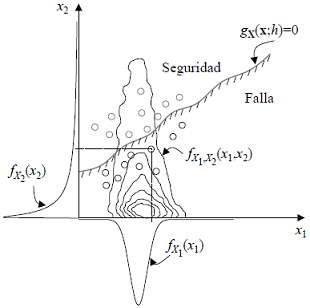
Sea xT =[X1, X2,…, XN] un vector de estado que contiene variables aleatorias básicas de diseño X1, X2,…, XN con densidades de probabilidad conjunta N -variadas, representadas por fx(x). Por simplicidad, los eventos de seguridad y falla ante un mecanismo específico se describen en términos de una función de estado gX(x), escrita de tal manera que {gX(x) ≥ 0}, representa el evento de seguridad; i.e. {x ϵ S} y {gx(x) <0}, representa el evento de falla; i.e. {x ϵ 𝔍}. En particular, la probabilidad de que x se encuentre en 𝔍 es la probabilidad de falla Pf. Formalmente (Casciati y Faravelli, 1991)
La probabilidad de falla dado un valor específico h de la intensidad es la fragilidad y se puede expresar como
En la ec. 2 el dominio de falla depende de la intensidad h. La curva dada por FH(h) es la curva de fragilidad. La curva de fragilidad expresa la probabilidad de que la capacidad sea menor que la demanda dada, una intensidad h de la solicitación, y se puede interpretar entonces como la función de distribución acumulativa de la capacidad para el mecanismo de falla considerado. En esta interpretación, la capacidad se muestra en las mismas unidades de h. Conforme la intensidad aumenta, la probabilidad de falla se aproxima a la unidad.
Enfoque basado en el método de Monte Carlo
En este contexto, la probabilidad de falla se obtiene escribiendo la ec. 1 en la siguiente forma (Rubistein, 1987)
donde Θ representa el dominio de las variables aleatorias en x e I(x) es una variable aleatoria binaria tal que: I(x)=0, si g(x) ≥ 0 o I(x) = 1, si g(x) <0.
Para diferentes valores de h, se podrá definir entonces una curva de fragilidad empírica (punto por punto) como
El símbolo “^” encima de FH(h) enfatiza que la curva dada por la ec. 4 es una curva de fragilidad empírica. La versión teórica de la curva experimental se puede obtener por medio de algún procedimiento de ajuste, usualmente recurriendo al método de mínimos cuadrados.
Para determinar el valor que toma la variable aleatoria binaria I(x), es necesario simular las variables aleatorias del vector x. Para simular variables aleatorias no gaussianas correlacionadas se puede utilizar, por ejemplo, una alternativa basada en el método de descomposición de Cholesky (Rao, 1992), en la siguiente manera:
Especificar la matriz de correlación deseada en términos del “rho” de Spearman 𝜌s.
Obtener la matriz de correlación correspondiente R en términos del “rho” de Pearson 𝜌 como: 𝜌=2sen(π𝜌s/6).
Realizar la descomposición de Cholesky de R, tal que: R = ΓΓT.
Simular N variables aleatorias gaussianas independientes: zT = (Z1,Z2,…,ZN).
Hacer: y = Γz.
Obtener: U = Φ(y); donde Φ(·) es la función de distribución gaussiana.
Hacer: X1 = F1-1(U1), X2 =F2-1(U2),…, X N = FN -1(UN); donde Fj-1(·) para j=1,2,…, N son los inversos de las funciones de distribución deseadas.
Con el procedimiento anterior es posible determinar la probabilidad de falla para diferentes valores de la intensidad h por medio de la ec. 4. La interpretación geométrica de dicho cálculo para un caso ilustrativo con dos variables aleatorias se muestra en la Figura 1. Debido a que las variables aleatorias del vector y se obtienen como una combinación lineal de las variables gaussianas en z, las densidades de probabilidad conjuntas de las variables aleatorias del vector y serán gaussianas con matriz de correlación dada por Γ.
Enfoque basado en el método FORM
Sea zT=[Z1,Z2,…,ZN] un vector que contiene variables aleatorias Z1,Z2,…,ZN gaussianas estandarizadas, independientes, con media cero y desviación estándar unitaria, con densidades de probabilidad conjunta N-variadas gaussianas, representadas por fz(z). En el conocido método de confiabilidad de primer orden (FORM), la función de estado se aproxima por medio de un hiperplano tangente a un punto z* y la probabilidad de falla se expresa como
donde α* representa un vector que contiene los cosenos directores de la normal al plano β+α*Tz*=0 y β corresponde a la distancia mínima del origen, en el espacio de las variables en z, al punto z* sobre la superficie de falla gz(z)=0. Debido a su simetría, fz(z) será invariante a cualquier rotación y su valor máximo a lo largo de gz(z)=0 ocurrirá en z*. Además, debido a que las variables en z son gaussianas, la variable aleatoria de la combinación lineal α*Tz* será gaussiana, con función de distribución acumulativa dada por Φ(∙) y β como su argumento. Hasofer y Lind (1974) propusieron utilizar β como un índice de confiabilidad que se puede obtener resolviendo el siguiente problema de optimación
El vector z que minimiza la ec. 6, sujeto a la restricción g z(z)=0, es z* y corresponde a un vector x* cuyos elementos definen el punto de diseño (x*ϵx). El punto de diseño es el punto de falla más verosímil. Dado un valor específico h de la intensidad, se tendrá un índice de confiabilidad β por medio de la ec. 6. La curva de fragilidad empírica se puede escribir por lo tanto como
Para determinar el índice β, Hohenbichler y Rackwitz (1981) proponen recurrir a la transformación de Rosenblatt con el propósito de transformar las variables originales en variables gaussianas no correlacionadas (Figura 2) y optimizar la ec. 6 con el algoritmo de Rackwitz y Fiessler (1978). La transformación de Rosenblatt mapea las variables en x a las variables en z a través de la ley de correspondencia dada como
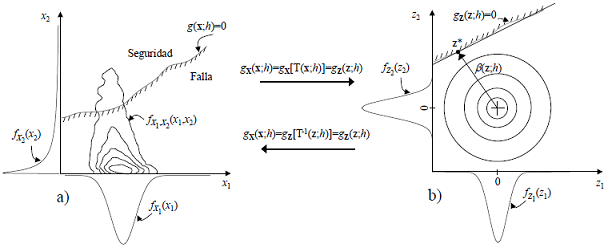
Figura 2 Ilustración de la región de falla y seguridad en función de la intensidad para una función de estado límite con dos variables aleatorias. Espacio de las variables aleatorias originales (izquierda). Espacio de las variables aleatorias transformadas (derecha)
donde:
La transformación inversa de Rosenblatt mapea las variables aleatorias en z a las variables en x de tal manera que
donde el inverso de la ley de correspondencia está dado por
Como una primera aproximación, en el presente artículo se considera que las densidades de probabilidad conjuntas entre variables aleatorias son gaussianas. Por lo tanto, las funciones de distribución acumulativas condicionales serán gaussianas. Utilizando la transformación de Rosenblatt y una variante del algoritmo descrito en Madsen et al. (1986), un punto de la curva de fragilidad en la intensidad h se puede calcular entonces de la siguiente manera:
Definir la matriz de correlación de las variables en x en términos del “rho” de Spearman 𝜌s.
Obtener la matriz de correlación correspondiente en términos del “rho” de Pearson 𝜌 haciendo: 𝜌 = 2sen(π𝜌s / 6).
Aplicar la transformación T al vector xj para obtener el vector zj. Usualmente, en la iteración j=1 se consideran los valores esperados de las variables aleatorias en x.
Obtener la matriz jacobiana: J=[ƏZi/ƏXj] y evaluar su inversa J-1.
Determinar la función gz(z) por medio de la ec. 9.
Calcular el gradiente de gz(z) como ∇gz(z)=(J-1)T ∇g(x). T indica “la transpuesta de”.
Obtener zj+1 =((zj)Tαj)αj-gz(zj)/|∆gz(zj)|; donde αj , es un vector unitario normal a gz(zj) dado por αj=∇gz(zj)/|∇gz(zj)|, siendo |∙|, la norma de ∇gz(zj).
Evaluar gz(zj+1 ). Si gz(zj+1)≅0, dentro de una aproximación aceptable, entonces obtener xj+1 =T-1(zj+1) y hacer x*=xj+1; z*=zj+1; α*=αj y βi =-(z*)Tα*. De lo contrario, ir al punto 3.
Repetir el procedimiento a partir del punto 3 con diferentes valores iniciales del vector xj y obtener: β=mín{β i ,…, β k }, donde i=1,2,…,k.
Observe que el nuevo vector x j+1 se obtiene aquí a partir de la solución analítica de la transformación inversa de Rosenblatt (punto 8), evitando así la recurrencia del algoritmo original que suele producir inestabilidades numéricas (Madsen et al., 1986). A la variante del método FORM descrita en este inciso se denomina en lo sucesivo método FORM-NG.
Análisis de la falla por erosión de un bordo perimetral sometido a un desbordamiento
Para ilustrar los resultados que se obtienen con el método de Monte Carlo (MC) y el método FORM-NG descritos atrás, en este inciso se comparan las curvas de fragilidad de un bordo perimetral para la falla por erosión debida al desbordamiento y se evalúa el desempeño general de ambos métodos.
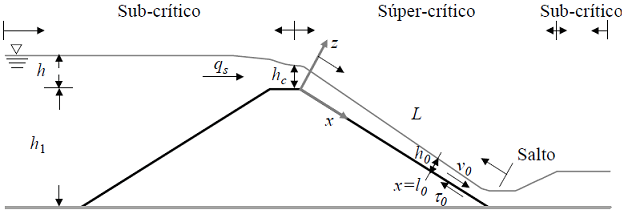
La falla por erosión se refiere a la ruptura parcial o total de un bordo sometido a un flujo de agua sobre su superficie. Esta condición representa la principal causa de falla en presas (Foster et al., 2000). El modelo teórico comúnmente aceptado que describe el flujo a superficie libre sobre un bordo perimetral durante un desbordamiento gradual (sin oleaje) se muestra en la Figura 3 (Powledge et al., 1989). El efecto erosivo del agua se puede cuantificar recurriendo a la ecuación de momento de Saint-Venant para flujo establecido unidimensional de donde se obtiene el esfuerzo cortante en la interfaz suelo-agua (Nadal y Hughes, 2009). Para determinar la tasa de erosión del material del bordo, con frecuencia se recurre a la ecuación del exceso del esfuerzo cortante (Zhao et al., 2015; Partheniades, 1965). Con base en esta última formulación, la ecuación de estado límite se puede escribir entonces en la siguiente forma
donde
ξ |
= erosión [mm] |
t |
= tiempo [h] |
kd |
= coeficiente de erosionabilidad [mm/h/Pa] |
τc |
= esfuerzo cortante crítico [Pa] |
τ0 |
= esfuerzo cortante en la interfaz suelo-agua [Pa] |
donde
𝜌 |
= densidad del agua [kg/m3] |
g |
= aceleración de la gravedad [m/s2] |
h0 |
= tirante de agua normal a la superficie del talud en régimen establecido |
Aguas abajo, el flujo es súper-crítico y el tirante normal al talud se puede obtener por medio de la fórmula para vertedores de cresta amplia (Henderson, 1966) y la ecuación de Manning en la siguiente forma
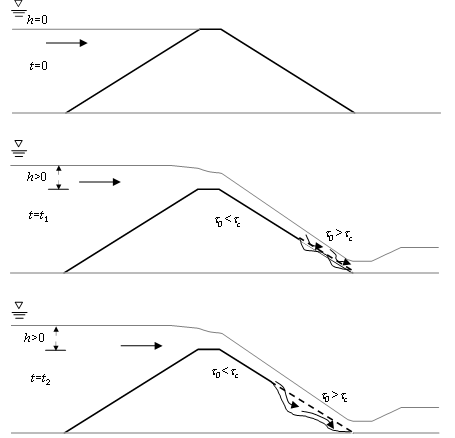
Cuando τ0 > τ c , la erosión del bordo ocurre a una velocidad dada por k d (Figura 4).
El umbral ξ determina la frontera entre la región de falla y seguridad. La experiencia muestra que un bordo de material fino compactado usando procedimientos modernos de compactación bajo un estricto control de calidad, puede tolerar una erosión superior a un metro de profundidad sin comprometer su seguridad (Hughes, 2010; Yuan et al., 2015). En el presente trabajo se adopta una escala de erosión permisible arbitraria en la siguiente forma:
Daño menor: Si la erosión es mayor que 0.30m
Daño intermedio: Si la erosión es mayor que 0.60m
Daño severo: Si la erosión es mayor que 0.90m
Se considera una situación de la práctica en la que el diseñador tiene incertidumbre en la estimación de cuatro variables básicas de diseño: n, τ c , k d y 𝜃. Estas incertidumbres se representan por medio del vector de variables aleatorias: x T = {X 1,…,X 4}. Las fragilidades se determinan para diferentes muestras de una variable aleatoria que refleja las fluctuaciones del nivel de agua en el embalse dentro del intervalo: 0 ≤ h ≤ 2. Los parámetros del conjunto de variables aleatorias básicas de diseño se indican en la Tabla 1. Estas variables y sus parámetros reflejan el conocimiento limitado que prevalece en la mente del diseñador. La dependencia entre las distintas variables aleatorias se indica por medio del coeficiente de correlación de Spearman en la Tabla 2. Se ha considerado que existe correlación entre los tres parámetros que dependen del tipo de material del bordo.
Tabla 1 Parámetros probabilistas de las variables básicas de diseño
| Parámetro | Unidad | E{X} | CV | Mín. | Máx. | Tipo |
|---|---|---|---|---|---|---|
| n | s/m1/3 | 0.0158 | 0.1 | 0.01 | 0.035 | Beta |
| τc | Pa | 16 | 6 | 0.0 | ---- | Lognormal |
| kd | mm/h/Pa | 2.5 | 6 | 0.1 | ---- | Weibull |
| θ | rad | 0.197396 | 0.1 | ---- | ---- | Normal |
Tabla 2 Correlación entre las variables básicas de diseño
| Coeficiente de correlación de Spearman | |||||
|---|---|---|---|---|---|
| Parámetro | θ | n | τc | kd | |
| n | 0.0 | 1.0 | -0.8 | 0.8 | |
| τc | 0.0 | -0.8 | 1.0 | -0.7 | |
| kd | 0.0 | 0.8 | -0.7 | 1.0 | |
| θ | 1.0 | 0.0 | 0.0 | 0.0 | |
La fragilidad del bordo se analiza para dos tiempos de permanencia del desbordamiento; es decir, para un periodo de 4h y otro de 20h. En la evaluación de las fragilidades con el método de Monte Carlo se consideran 500,000 simulaciones en cada caso.
Resultados y discusión
Las Figuras 5 y 6 muestran con símbolos las curvas de fragilidad empíricas para permanencias del desbordamiento de 4 y 20h, respectivamente. Los círculos corresponden a las fragilidades del método MC y los triángulos a las del método FORM-NG. Los resultados de ambos enfoques proporcionan resultados prácticamente idénticos cuando la permanencia del desbordamiento es de 4h. Cuando la permanencia del desbordamiento aumenta a 20h se observan pequeñas diferencias entre los resultados de ambos enfoques para desbordamientos cercanos a 2m, en los daños intermedio y severo. En otras palabras, las pequeñas diferencias ocurren cuando la probabilidad de falla se aproxima con mayor rapidez a uno, es decir, cuando el índice de confiabilidad tiende a ser más rápido a un valor muy pequeño. En esta situación, la no linealidad de la función de estado hace que el método de optimación quede atrapado fácilmente en un mínimo local. Otros métodos de optimación más robustos se pueden incorporar fácilmente en el contexto de la metodología descrita en el presente artículo y aumentar así su exactitud (Wang et al., 2016; Ezzati et al., 2015). La forma de la curva de fragilidad, sin embargo, se captura contundentemente con el método FORM-NG en un tiempo de cálculo muy inferior al del método MC comúnmente utilizado por varios autores (Popescu et al., 2005; Zentner, 2010). Además, el método FORM-NG permite modelar las incertidumbres en las variables de diseño de una manera más realista por lo que la evaluación de la curva de fragilidad resulta menos subjetiva que las aproximaciones utilizadas en los métodos de factores de seguridad (Kennedy et al., 1980; Pisharady y Basu, 2010).
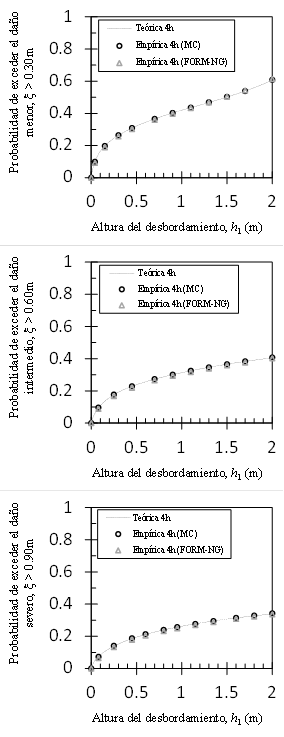
Figura 5 Comparación entre las curvas de fragilidad empíricas y la curva de fragilidad teórica para una permanencia del desbordamiento igual a 4h
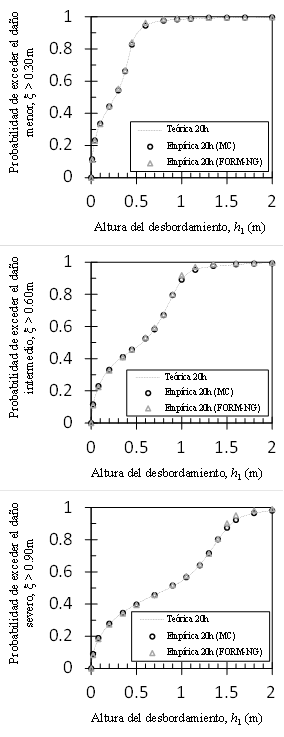
Figura 6 Comparación entre las curvas de fragilidad empíricas y la curva de fragilidad teórica para una permanencia del desbordamiento igual a 20h
En las Figuras 5 y 6 se observa además, que conforme la duración del desbordamiento aumenta la probabilidad de falla también aumenta, pero conforme el umbral de falla ξ aumenta la probabilidad de falla disminuye. Este último resultado se debe a que la frecuencia con la que ocurre una falla más severa es menor si se mantienen constantes los parámetros probabilistas de las variables básicas de diseño. Para un desbordamiento próximo a 2m y una duración de 20h, el bordo alcanza la falla con probabilidad muy cercana a uno. Adoptando la interpretación de Shinozuka (2000), las curvas de fragilidad en las Figuras 5 y 6 representan la probabilidad de que el bordo sufra al menos el daño especificado cuando se somete a un desbordamiento con intensidad h.
En los análisis de fragilidad tradicionalmente se supone a priori una distribución lognormal para la curva de fragilidad teórica y sus parámetros se obtienen posteriormente en forma estadística. Para determinar la forma de la curva de fragilidad teórica se ajustó por medio del método de mínimos cuadrados una función de distribución acumulativa a cada curva experimental del método MC. Se encontró que la curva teórica está dada por una distribución de Weibull compuesta (Razali y Al-Wakeel, 2013) en la siguiente forma:
donde
Gx(x) |
= función de distribución compuesta |
wj |
= ponderación asociada a la j-ésima distribución de Weibull |
F x(x) |
= función de distribución de Weibull dada por: F x (x) = 1 ˗ exp[ ˗ (x/𝛼)𝛽] con parámetros de escala y forma dados por 𝛼 y 𝛽, respectivamente. |
Las curvas de fragilidad teóricas se muestran con líneas discontinuas en las Figuras 5 y 6. Los parámetros que definen estas curvas se indican en la Tabla 3. Las curvas de fragilidad teóricas difieren, por tanto, significativamente de la distribución lognormal. La influencia de la densidad de probabilidad del parámetro k d sobre el tipo de curva de fragilidad es entonces mayor que la influencia de las densidades de probabilidad de las variables n, τ c y θ. La forma de la curva de fragilidad teórica dada por la ecuación 14 se puede explicar por el efecto no lineal de la función de estado sobre la densidad de probabilidad de k d . Cálculos preliminares mostraron que la correlación entre las variables de diseño modifica los parámetros de las curvas teóricas pero no cambian el tipo.
Tabla 3 Parámetros probabilistas de las curvas de fragilidad teóricas
| Daño | Duración | Ponderación | Escala | Forma | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| w 1 | w 2 | w 3 | α 1 | α 2 | α 3 | β 1 | β 2 | β 3 | ||
| Menor | 4h | 0.179 | 1.303 | 0.277 | 0.065 | 3.867 | 0.672 | 0.804 | 3.120 | 1.167 |
| 20h | 0.184 | 0.551 | 0.263 | 0.419 | 0.112 | 0.434 | 9.029 | 0.601 | 3.014 | |
| Intermedio | 4h | 0.196 | 0.120 | 0.181 | 0.163 | 1.459 | 1.898 | 0.762 | 0.981 | 1.405 |
| 20h | 0.414 | 0.505 | 0.208 | 0.893 | 0.255 | 9.815 | 5.872 | 0.636 | 0.355 | |
| Severo | 4h | 0.083 | 0.354 | 0.037 | 0.936 | 1.776 | 0.102 | 0.613 | 0.714 | 0.714 |
| 20h | 0.345 | 0.525 | 0.446 | 1.392 | 3.560 | 0.686 | 7.480 | 0.571 | 0.516 | |
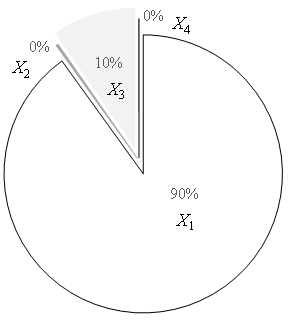
Además de su eficiencia computacional, otra ventaja que ofrece el método FORM-NG es la posibilidad de evaluar la sensibilidad de la falla a cada una de las variables aleatorias básicas de diseño por medio de los cosenos directores que contiene el vector 𝛼*, sin necesidad de realizar análisis estadísticos adicionales, como sucedería con el método MC. En estricto rigor, la influencia de las variables de diseño sobre la falla del bordo cambia con la intensidad de la solicitación, sin embargo, se pueden destacar las principales tendencias mostradas en el diagrama de la Figura 7. En dicha figura se puede observar que la falla por erosión del bordo es significativamente más sensible a la incertidumbre del coeficiente n de Manning, y que las incertidumbres en el esfuerzo cortante crítico τ c y el ángulo de inclinación 𝜃 del talud aguas abajo sobre dicha falla son prácticamente despreciables. Destaca que la influencia del coeficiente de erosionabilidad k d del material del bordo sobre la falla sea considerablemente inferior a la del coeficiente n de Manning y que aun así influya sobre el tipo de curva de fragilidad. Por lo tanto, el tipo de densidad de probabilidad de la variable aleatoria con mayor influencia sobre la falla del bordo no necesariamente determina el tipo de curva de fragilidad. En un contexto más realista de incertidumbres no gaussianas, no parece correcto suponer a priori un modelo teórico para la curva de fragilidad ignorando las distribuciones de las variables básicas, ya que no se puede anticipar su tipo teniendo en cuenta únicamente la distribución de la variable aleatoria con mayor incidencia sobre la falla del componente. El coeficiente de variación de las variables básicas podría tener un efecto sobre el tipo de curva de fragilidad. Sin embargo, un escenario distinto al que muestra la Tabla 1 no sería representativo de los contrastes que existen entre las variaciones de los parámetros. En efecto, la variabilidad de τ c y k d siempre será significativamente mayor que la variabilidad de n y 𝜃.
Conclusiones
Este artículo describe cómo se pueden modificar dos métodos clásicos de la confiabilidad estructural con el propósito de considerar incertidumbres no gaussianas correlacionadas en las variables básicas de diseño al evaluar la fragilidad estructural de componentes. Una de estas metodologías modificadas se basa en el método de Monte Carlo (MC) y la otra en el método de confiabilidad de primer orden (FORM). La variante del segundo método se ha denominado aquí “método FORM-NG”.
El desempeño general de ambos métodos se evaluó comparando las curvas de fragilidad para la falla por erosión asociada al desbordamiento de un bordo perimetral. El método MC y el método FORM-NG proporcionaron resultados muy semejantes debido a que ambos toman en cuenta la información completa de las variables aleatorias y suponen un mismo tipo de dependencia, es decir, ambos métodos suponen que la dependencia entre las variables de diseño es gaussiana y que se puede cuantificar a través del coeficiente de correlación de Spearman. Se observaron pequeñas diferencias en algunos casos, específicamente, cuando la probabilidad de falla se aproxima rápidamente a uno, es decir, cuando el índice de confiabilidad tiende rápidamente a un valor muy pequeño. Tales diferencias se pueden asociar a la no linealidad de la función de estado. Sin embargo, debe destacarse que la forma de la curva de fragilidad se captura muy satisfactoriamente utilizando el método FORM-NG y que su eficiencia en términos de tiempo de cálculo es superior a la del método de Monte Carlo.
En la práctica, la curva de fragilidad teórica se multiplica por la curva asociada a la amenaza específica para obtener la probabilidad de falla anualizada del componente respecto al mecanismo y amenaza específicos. El tipo de curva de fragilidad tendrá entonces consecuencias importantes en la cuantificación del riesgo. Por lo tanto, es recomendable que el efecto del tipo de densidad de las variables básicas de diseño sobre el riesgo se evalúe en todos los casos. En la práctica profesional el diseñador encontrará estructuras expuestas a múltiples modos de falla, pero la curva de fragilidad para cada modo se podrá evaluar con los métodos descritos en este artículo. Las metodologías son generales y se pueden utilizar en el análisis estocástico de la falla de componentes.











 text new page (beta)
text new page (beta)