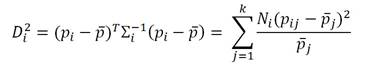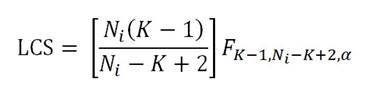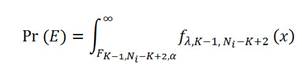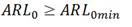Introducción

La calidad es un aspecto imprescindible en la fabricación de productos. Hay factores que introducen variación en un proceso de producción, por ejemplo, la materia prima varía de lote en lote y las máquinas y herramientas se desgastan. Entonces, resulta necesario que los procesos operen bajo condiciones de variación que no representen un problema en la calidad del producto. Para este fin se desarrollaron herramientas estadísticas, llamadas gráficos o cartas de control estadístico, que sirven para monitorear la variación presente en los procesos y ayudan a identificar cuando ocurra algún cambio en la misma. Su utilización contribuye a la reducción de la variabilidad del proceso; permitiendo mejorar su calidad.

Una clasificación general de las cartas de control se muestra según el tipo de variable capaz de monitorear, a saber se dividen en, cartas de control para variables continuas y variables discretas, conocidas como cartas para variables y cartas para atributos, respectivamente. Las primeras son útiles para monitorear variables que se pueden expresar en alguna escala continua de medición, por ejemplo, el diámetro interno de un rotor para uso automotriz. Por su parte, los gráficos de control para atributos se usan cuando la variable se expresa en una escala nominal u ordinal, es decir, la variable se expresa como una clasificación de artículos según ciertas características o atributos. Por ejemplo, en lugar de obtener la medida del diámetro del rotor se emplea un dispositivo mediante el cual es posible decidir si la pieza tiene el diámetro correcto o no, sin necesidad de obtener la magnitud exacta. En este caso, la pieza se clasifica como conforme si se determina que el diámetro es el correcto y como no conforme en caso contrario, también se le conoce como variables categóricas.

En 1924, Walter A. Shewhart introdujo la primera carta de control para variables. Desde entonces, se han propuesto nuevos enfoques, generalizaciones y modificaciones. Por ejemplo, las cartas de control adaptativas consideran tamaños de muestra variables o frecuencia variable de muestreo o ambos (^{Mahadik and Shirke 2011}; ^{Seif et al. 2011}; ^{Faraz et al. 2012}). En las cartas de control con muestreo secuencial, el muestreo en fases según la localización de los valores del estadístico de prueba (^{Irianto and Juliani 2010}; ^{Khoo et al. 2010}; ^{Costa and Machado 2011}). Otro tipo de cartas de control, llamadas sintéticas, combinan una carta de control clásica y el monitoreo de una variable aleatoria, que puede ser el número de muestras inspeccionadas entre dos señales fuera de control (^{Ghute and Shirke 2008}; ^{Khoo et al. 2010}).

Con frecuencia las cartas de control se emplean para detectar cambios inusuales en variables que son independientes y no influenciadas por el comportamiento de otras variables (cartas de control univariado). Sin embargo, hay muchos entornos industriales donde el desempeño del proceso se basa en el comportamiento de un conjunto de variables relacionadas entre sí (^{Mason y Young 2002}). En estos casos, el uso de una carta de control univariado puede no ser apropiado debido a que solo pueden monitorear una variable a la vez y no consideran su posible correlación. Los procedimientos de control multivariado, por su parte, están diseñados para monitorear más de una variable simultáneamente y considerar la relación entre ellas. Para una revisión de cartas de control multivariado para variables ver ^{Bersimis et al. (2007}). Este trabajo se enfoca a cartas de control multivariado para atributos, es decir, a cartas de control multiatributo.

Algunos enfoques que consideran el monitoreo simultáneo de más de un atributo de calidad en una misma gráfica son, por ejemplo, ^{Lu et al. (1998}) quienes desarrollaron una carta llamada MNP basada en la distribución binomial. Ellos definieron el estadístico X con la suma de conteos de unidades no conformes de todas las características de calidad en una muestra. Por su parte, ^{Jolayemi (1999}) propuso un modelo para controlar procesos multiatributo, el cual es una extensión de la carta univariada np. Se supone que los atributos del proceso son variables aleatorias binomiales independientes.

Adicionalmente, ^{Taleb y Liman (2005}) y ^{Niaki y Nasaji (2011}) propusieron cartas de control multiatributo basadas en técnicas estadísticas y de inteligencia artificial. Un enfoque sintético para datos categóricos se propuso por ^{Li et al. (2014}).

Cuando se monitorea un proceso es necesario extraer muestras del proceso e inspeccionarlas, esto representa un costo. Es común, que las cartas de control por atributos requieran mucha más información para operar, con cierta precisión estadística, que las cartas para variables.

Hay procesos donde recolectar muestras de gran tamaño es difícil, por ejemplo, cuando el estándar de producción es bajo, o cuando la inspección requiere pruebas destructivas, o simplemente, para reducir el costo de inspección. En particular, en un proceso de soldadura para la industria automotriz, una pieza se clasifica en siete defectos de asociados a la soldadura, dicho proceso, de hecho, tiene bajo volumen de producción. Entonces, existe un problema cuando se monitorean procesos multiatributo y tienen que considerarse restricciones en el uso de muestras de gran tamaño.

La carta de control D², propuesta por ^{Mukhopadhyay (2008}), no se basa en la distribución Chi cuadrada. Esto implica que, en teoría, no se requieran tamaños grandes de muestra para funcionar de manera eficiente. Para obtener una buena aproximación a la Chi cuadrada es necesario que el número esperado de piezas por atributo sea de al menos 5. De otra manera, se hace una corrección por finitud, por ejemplo la propuesta por ^{Yates (1934}). Sin embargo, resulta necesario comprobar que la carta propuesta por Mukhopadhyay es eficiente con muestras pequeñas y determinar si es una alternativa adecuada para situaciones como las descritas en el párrafo anterior. Con este fin, en este trabajo se estudia el desempeño de la carta con diferentes tamaños de muestra para investigar el efecto de reducir el tamaño de muestra sobre la eficiencia de la carta. Adicionalmente se presentan diseños óptimos de carta para diferentes escenarios. El desempeño se midió en términos de la longitud promedio de corrida (ARL, Average Run Length). Los resultados sugieren que la carta de control no puede ser eficiente cuando el tamaño de muestra es pequeño, por tal motivo se buscaron diseños óptimos que maximizan la eficiencia de la carta para esos casos.

Este artículo se organiza de la siguiente manera: la introducción se presenta en la primera sección, la segunda sección contiene el desarrollo de la investigación, siguiendo con el análisis y discusión de resultados en la tercera sección. Finalmente, se presentan las conclusiones.

Desarrollo

Enseguida se expone una descripción del gráfico D². Este gráfico se propuso por ^{Mukhopadhyay (2008}) y es capaz de monitorear más de un atributo simultáneamente. Se basa en una generalización de la distancia de Mahalanobis y en la distribución multinomial. Este gráfico se adecua para monitorear procesos que puedan describirse de la siguiente manera:

Durante un proceso de producción, un artículo terminado se clasifica en una y solo una de 𝑘 categorías de defectos incluyendo la categoría de piezas conformes, es decir, hay k - 1 defectos en total. Sea p_ij la proporción observada de artículos clasificados en la categoría j, j=1,2,…,k, en una muestra de tamaño N_i, y (Ƥ_i1,Ƥ_i2,Ƥ_i3,…,Ƥ_ik) = Ƥ_i^T es el vector de proporciones asociadas a cada categoría. Ahora suponga que p-T = [p-1, p-2, ..., p-k] denota el vector de categorías no conformes en un proceso bajo control. p-T puede estimarse mediante una base histórica de datos o especificarse arbitrariamente. Entonces, p_i^T tiene una distribución multinomial con parámetro p-T. En lo consecutivo, p-T se referirá como vector objetivo. Es claro que el vector objetivo se fija para representar un proceso de alta calidad: proporciones bajas en las categorías no conformes y proporción alta en la categoría conforme.

Para el caso multinomial, una distancia de Mahalanobis generalizada se define como

(1)

Donde, D_i² mide, en un punto particular de tiempo, la distancia entre el vector de proporciones observadas y el vector de proporciones objetivo. El límite de control superior (LCS) es

(2)

La cantidad, F_{K-1,Ni-K+2,α} es el cuantil α de la distribución F con (K - 1) y N_i - K+2 grados de libertad. El límite de control inferior es cero. Ver ^{Mukhopadhyay (2008}) para más detalles.

Una medida de desempeño comúnmente utillizada para evaluar la eficiencia de una carta de monitoreo es el ARL. El ARL mide la rapidez con que la carta detecta un cambio en la calidad. Se supone que el proceso arranca dentro de control, es decir, p- = p-0; y en algún tiempo después la calidad del proceso decrece (p- = p-1). A continuación se presenta una breve descripción del ARL.

La longitud promedio de corrida (ARL) se usa para medir la rapidez con la que una carta de control detecta un cambio o una perturbación del proceso que afecta la calidad del producto. El ARL se define como el número promedio de muestras que se requieren para que la carta muestre una señal fuera de control. Si las observaciones graficadas en la carta de control son independientes, entonces el número de puntos graficados hasta que un punto excede un límite de control es una variable aleatoria geométrica como parámetro p. La media de la distribución geométrica es 1/p.

Una carta de control es una secuencia de pruebas de hipótesis. Entonces existen errores asociados conocidos como error tipo I y error tipo II, que consisten en rechazar la hipótesis nula si es cierta y aceptar la hipótesis nula si es falsa, respectivamente. En este contexto, la hipótesis nula establece que el proceso se encuentra dentro de control. Entonces, el error tipo I ocurre cuando el proceso se declara fuera de control cuando no es así; a esto se le conoce como una falsa alarma. En este caso, el ARL se denota por ARL₀ y se desea que sea grande, de forma que se tengan pocas falsas alarmas. El ARL₀ se expresa en (3). Por otra parte, cuando el proceso está fuera de control, el ARL debe ser pequeño para proveer una rápida detección de perturbaciones en la calidad del proceso. En este caso, se denota por ARL₁ y se calcula mediante (4).

(3)

Donde P es la probabilidad de cometer error tipo I; cuando esta probabilidad se especifica se denota con la letra α.

(4)

Donde, P es la probabilidad de concluir que el proceso está fuera de control y que la hipótesis nula (el proceso está dentro de control) es falsa. Se calcula como el complemento de β, que denota la probabilidad de cometer el error tipo II. Es fácil ver que el valor mínimo de ARL es 1. Hay dos formas de calcular el ARL, una es obtener la expresión analítica de P y la otra es calcular un valor aproximado del ARL mediante simulación. En este trabajo se obtuvo la forma analítica de P, considerando las propiedades distribucionales del estadístico de prueba.

El evento “la carta señala un estado fuera de control” ocurre si E= {Di2 ≥ UCL}, entonces la probabilidad de que la carta señale un estado fuera de control está dada por

P = Pr(E)

Considerando la distribución de estadístico Di,j2,

La probabilidad Pr(E) se obtiene mediante

(5)

Donde f_{λ,K-1,Ni-K+2} (∙) es la función de densidad de una distribución F no central con parámetro de no centralidad λ y con K-1 y N _i-K+2 grados de libertad. α, la probabilidad de un error tipo I, es fijo y la cantidad F_{k-1,Ni-K+2,α} es el punto percentil (1 - α) de una distribución 𝐹 central con K-1 y N_i-K+2 grados de libertad. De hecho, α se fijó en 0.01. C= Ni(K-1)Ni(K+2).

Resultados y discusión

Obtención de las curvas de potencia

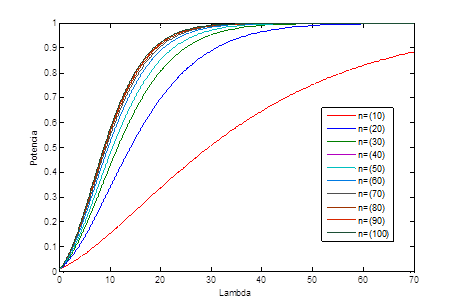
Para estudiar el desempeño de la carta, se obtuvieron con (7) las curvas de potencia suponiendo número de categorías K= {3,6} y con tamaños de muestra n, n = {10,20,30,40,50,60,70,100}. Los resultados se muestran en las Figuras 1 y 2, respectivamente. Como el ARL está en función de la potencia, por razones de apariencia se optó por mostrar las curvas de potencia en lugar de las de ARL.

Figura 1 Curvas de potencia de la carta D² para K = 3 

Figura 2 Curvas de potencia de la carta D² para K = 6 

Como puede observarse en las Figuras 1 y 2, el tamaño de muestra tiene una influencia importante en el desempeño de la carta. Por ejemplo, la carta tiene el mejor desempeño cuando n=100 y el peor cuando n=10. Aunque en ^{Mukhopadhyay (2008}) se sugiere que la carta no debería presentar problemas relacionados al tamaño de muestra, con los resultados obtenidos, se demuestra que la carta no puede ser eficiente cuando el tamaño de muestra es pequeño. Las curvas con el peor desempeño para K=3 son las que corresponden a n = {10,20,30} y para K=6 son n = {10,20,30,40,50}. Además, puede observarse que el efecto es mucho mayor si el número de categorías K se acerca a n, el tamaño de muestra, así por ejemplo, la potencia de la carta para n = 10 es mucho menor para K= 6 que para K= 3, recordando que es deseable que la potencia, la probabilidad de declarar que el proceso está fuera de control sea grande, cuando λ > 0, que representa un proceso multinomial fuera de control estadístico.

Diseño óptimo de la carta D²

Para implementar el gráfico de control D², se requiere seleccionar los parámetros de diseño N y LCS. Usualmente, la selección se hace considerando en ARL.

En este caso, se requiere especificar el ARL dentro control mínimo (ARL_0min), el número de categorías (C), el tamaño de muestra máximo total (n_max) y la magnitud del corrimiento de calidad (s) que se desea monitorear. Tal información debe proveerse por el especialista del proceso. Se usó un método de optimización, basado en un algoritmo genético (AG), para encontrar los mejores parámetros de diseño x* = [N, LCS], el valor del tamaño de la muestra N, del límite de control LCS que minimicen el ARL₁ con ARL_0, s y n_max fijos. Formalmente

Donde P se calcula con la expresión (4), con λ > 0.

Sea χ el espacio de búsqueda, donde x* ϵ χ. Las restricciones son:

(6)

(7)

(8)

(9)

(10)

Donde (6) resulta de (n_i - C + 2), (7) de (C - 1) los grados de libertad de la distribución F en (5), esas cantidades deben ser iguales o mayores que 1, entonces K ≤ N + 1. La expresión (8) surge de la idea que el tamaño de muestra debe limitarse para acotar la búsqueda a regiones de interés, de acuerdo con restricciones prácticas. La ecuación (9) es una restricción técnica. Por otra parte, el estadístico de prueba es una distancia, por lo tanto, no es negativa, así el límite de control no debe ser negativo, lo cual se especifica en (10). Los valores K, n_max , ARL_0min y s son entradas para el problema, en la práctica esta información se obtiene del proceso.

En este modelo se necesita la solución x*= (x_i |i=1,2,…,r) que minimiza ARL₁ , así que el conjunto de parámetros x* ϵ χ debe determinarse. El algoritmo genético (GA, Genetic Algorithm) usa una representación binaria de una posible solución. Esta codificación se necesita ya que el GA manipula bits. En el modelo se empleó una representación binaria de dieciséis por cada solución. La matriz de población inicial fue de 100 filas, que representan cada bit de la solución binaria codificada, es decir, cada individuo en la población representa un conjunto de (r×r) soluciones codificadas de 16 bits. Se empleó selección por torneo de tamaño 2 con cruce de un solo punto y una mutación simple. Las probabilidades de cruce y mutación fueron de 0.9 y 0.1, respectivamente. El ARL₁ definido en la ecuación (4) se usó como una función de evaluación con 200 generaciones en el GA.

Los parámetros de diseños que se muestran en la Tabla 1, se obtuvieron suponiendo ARL_0min = 200, numero de categorías C = {3, 6,9}, n_max ={20,30}, y se consideraron magnitudes de corrimiento s = {0.5,1.0,1.5,2.0,2.5,3.0}. Para cada combinación de valores, se encontró un diseño óptimo mediante un GA (optimización local, ver Tabla 1). Por ejemplo, se obtuvo un diseño óptimo para K = 3 y s = 0.5. Lo mismo se hizo para K = 6 y s = 1, así sucesivamente.

Tabla 1 Diseños para la carta D² con LCS = C lcs  

El valor ARL_0min = 200 se eligió porque se consideró una búsqueda de diseños con tamaños de muestra pequeños. Seleccionar un valor grande (el valor estándar es 370) puede llevar a tamaños de muestra muy grandes para asegurar una potencia de detección razonable (^{De Araújo et al., 2011}).

Los diseños de la Tabla 1 se pueden utilizar para monitorear procesos con características similares a los escenarios probados, únicamente se elige la magnitud de corrimiento que se desea monitorear. El empleo de alguno de estos diseños supone que el tamaño de muestra permanecerá fijo, esto implica una modificación al procedimiento de la carta D², el cual considera variar el tamaño de muestra de forma arbitraria.

El valor ARL_0min = 200 se eligió porque se consideró una búsqueda de diseños con tamaños de muestra pequeños. Seleccionar un valor grande (el valor estándar es 370) puede llevar a tamaños de muestra muy grandes, para asegurar una potencia de detección razonable (^{De Araújo et al., 2011}).

Los diseños que se muestran en la Tabla 1 se pueden utilizar para monitorear procesos con características similares a los escenarios probados, solo debe elegirse la magnitud de corrimiento que se desea monitorear. El empleo de alguno de estos diseños supone que el tamaño de muestra permanecerá fijo, esto implica una modificación al procedimiento de la carta D², el cual considera variar el tamaño de muestra de forma arbitraria.

Conclusiones

La carta de control D² es una herramienta recomendable para monitorear procesos multinomiales. Sin embargo, el método supone qué tamaño de muestra puede variar arbitrariamente, lo cual implica que la potencia de la carta será distinta en cada muestreo, siempre que el tamaño de muestra sea diferente.

Se estudió el desempeño de la carta D², los resultados sugieren que cuando el tamaño de muestra es pequeño (menor a 30 para K = 3, menor a 50 para K = 6) se espera que la carta no sea eficiente.

Mediante un algoritmo genético se buscaron diseños que mejoren el desempeño de la carta en situaciones que se espera sean deficientes (tamaño de muestra pequeño). De esta manera, se presentan diseños para diferentes escenarios, los cuales pueden utilizarse para el monitoreo de procesos multinomiales que tengan características similares. Elegir alguno de estos diseños para monitorear un proceso, implica fijar el tamaño de muestra, lo que evitará que la potencia de la carta tenga fluctuaciones.

Cuando se emplea una carta de carta de control multivariable o multiatributo, y la carta da una señal fuera de control, esta representa la información contenida en las variables o atributos que se monitorean. Sin embargo, es común que no sea posible establecer, de manera específica, cuál o cuáles variables son las que provocan que el proceso salga de control. De tal manera que resulta necesario un método para identificar el atributo que con mayor probabilidad provoque una situación fuera de control. Este método tendría un impacto práctico, debido a que brindaría información útil para encontrar la causa raíz del problema. Investigar un método como el descrito aplicable a la carta de control estudiada se deja como trabajo futuro.