Optimización de forma de un cuerpo suspendido basada en reglas evolutivas y modelado paramétrico: la forma de un fruto

 

Shape Optimization of a Hanging Body Based on Evolutive Rules and Parametric Modeling: The Shape of a Fruit

 

Velázquez-Villegas F.¹ y Santillán-Gutiérrez S.D.²

 

¹ Centro de Diseño Mecánico e Innovación Tecnológica Facultad de Ingeniería Universidad Nacional Autónoma de México. Correo: fernvel@unam.mx

² Centro de Alta Tecnología Facultad de Ingeniería Universidad Nacional Autónoma de México. Correo: saulsan@unam.mx

 

Información del artículo: recibido: junio de 2009.
Aceptado: junio de 2012.

 

Resumen

En este trabajo se desarrolla la optimización de forma de un cuerpo suspendido y sometido a fuerzas de cuerpo. La geometría del cuerpo es modelada con curvas paramétricas B-Spline. Dicha optimización se logra por medio de la modificación del contorno de la geometría con base en el nivel de esfuerzo calculado usando Análisis por Elementos Finitos. Reglas evolutivas clásicas son empleadas en el proceso de optimización; sin embargo, el método para realizar la modificación del contorno de la geometría no es ni clásico ni trivial. A diferencia de la mayoría de los métodos de optimización de forma, que utilizan sólo la información de los puntos del contorno aisladamente, en este trabajo se aplica un método que toma en cuenta la información de los puntos del contorno y su vecindad.

Descriptores: diseño óptimo, optimización de forma, optimización estructural, análisis por elementos finitos.

 

Abstract

This paper develops the shape optimization of a body, which is hanged and subjected to body forces. The geometry of the body is modeled using parametric curves B-Spline. The shape optimization is carried out modifying the boundary of the body based on the stress level calculated via Finite Element Analysis (FEA). Traditional evolutive rules are used for the optimization process; however, the method of boundary modification in the optimization process is neither traditional nor trivial. Unlike most shape optimization methods, which only use the information of boundary points in an isolated way, in this approach the geometry boundary is modified considering both points and neighborhood information.

Keywords: optimal design, shape optimization, structural optimization, finite element analysis.

 

Introducción

Los métodos de optimización pueden agruparse en dos tipos: métodos basados en el gradiente y métodos heurísticos. Los primeros implican que los problemas a resolver están representados por funciones continuas de las que es necesario calcular sus derivadas para obtener sus mínimos (máximos). Por otra parte, los métodos heurísticos no requieren derivadas ni funciones continuas, en lugar de ello, aplican iterativamente búsquedas seudoaleatorias, regidas por algunas reglas para obtener soluciones cercanas a la óptima.

Gracias al impresionante desarrollo de los equipos de cómputo, ahora es posible utilizar poderosos métodos numéricos, como el método de los elementos finitos (FEM) y el método de los elementos frontera (BEM), en la creación de algoritmos eficientes aplicados a la optimización estructural, cuya meta es obtener las mejores soluciones para problemas estructurales.

Uno de los problemas más interesantes en la optimización estructural es la optimización de forma. La pregunta fundamental en estos problemas es ¿cuál es la forma que debe tener una estructura bajo ciertas condiciones de operación para considerarse óptima? Para responder esta pregunta lo primero que se debe contestar es: ¿cuáles son las variables de diseño de las que depende la geometría de una estructura?

Pueden identificarse dos tipos de métodos en este sentido. En primer lugar aquellos que utilizan los elementos de una malla de elementos finitos como parte del conjunto de variables de diseño y en segundo lugar, los métodos que toman a los nodos en una malla (ya sea de elementos finitos o elementos frontera) como parte de las variables de diseño. Al primer conjunto pertenecen los métodos como ESO (Evolutionary Structural Optimization, Xie y Steven, 1997) en el que la optimización de la forma de una estructura se genera quitando material, es decir, quitando elementos en la periferia de la malla.

Por otra parte, métodos como los propuestos por Mattheck (1990, 1998, 2006), Ramm et al. (1998), Maute and Ramm (1995), Sethian y Wiegmann (2000), Cerrolaza et al. (2000), Annicchiarico y Cerrolaza (2001), Cervera y Trevelyan (2005a y 2005b), entre otros, pertenecen al segundo grupo en los que la frontera se modifica a partir de las características de los nodos en el contorno de la estructura. Una característica de este tipo es el resultado de aplicar una acción externa (sistema de fuerzas) sobre la estructura, es decir, esfuerzos, deformaciones, energía interna, etcétera.

La esencia que distingue a cada uno de los métodos no se encuentra en las reglas que siguen para evaluar la geometría de una estructura, sino en la forma en que la modifican. Aunque en apariencia todos actúan de la misma manera, es decir, aplicando gradual e iterativamente pequeños cambios en el contorno de la estructura, en realidad no son iguales.

El método de optimización utilizado en este trabajo para optimizar la forma del cuerpo suspendido (Velázquez, 2009; Velázquez y Santillán, 2012) actúa de manera similar a como lo hacen Mattheck, Cervera, Annicchiarico, entre otros. La frontera se desplaza en cada iteración con base en el nivel de esfuerzos existente en los nodos sobre ella. Guarda una similitud importante con lo propuesto por Cervera, en cuanto a que emplea las propiedades del modelado paramétrico para generar contornos suaves y evitar la aparición de concentradores de esfuerzo.

La diferencia fundamental se encuentra en el cálculo de los desplazamientos necesarios para cambiar el contorno de una estructura. La dirección de los desplazamientos de cada nodo sobre la frontera se calcula con base en la información de toda la vecindad en lugar de hacerlo con la información particular de cada uno de ellos. La información de la vecindad está dada por los valores de las funciones de interpolación con las que se modela la frontera; dichos valores son una medida de la influencia de los puntos de control en la posición de los nodos. El resultado es que, en lugar de generar desplazamientos perpendiculares al contorno, se producen desplazamientos cuya dirección considera la información de la vecindad en lugar de sólo la de un nodo en particular. En el siguiente apartado se describe el método propuesto por Velázquez.

 

Modelado paramétrico: curvas B-Spline

El cambio de posición de los nodos en una curva paramétrica B-Spline se realiza de manera indirecta al mover los puntos de control que definen dicha curva (figura 1). Lo anterior se hace patente si revisamos la definición de las curvas B-Spline.

Sean P₁, P₂, ... , P_m puntos de control de un polígono y u₁, u₂, ... , u_m valores de un parámetro u, con los cuales se pueden definir los m - 1 segmentos [u_i, u_i+1], donde i = 1, 2, ... , m - 1. Entonces, la curva B-Spline contenida por el polígono de los puntos de control y constituida por m - 1 polinomios de grado p se define como:

De esta definición se observa que realizar un cambio en los puntos de control genera que toda una región de la curva sufra modificaciones. Ahora bien, si dichas modificaciones están regidas por alguna característica medida sobre los nodos de la curva, entonces los cambios en los puntos de control deben tomar en cuenta los cambios necesarios en cada uno de los nodos que estén bajo su influencia.

 

Método

El método de optimización de forma utilizado en este trabajo suspendido (Velázquez, 2009; Velázquez y Santillán, 2012), se agrupa en el conjunto de métodos basados en estrategias evolutivas, debido a que emplea reglas basadas en parámetros que cambian gradual y lentamente (evolucionan) (Querin, 1997; Steven y Xie, 1993). La manera como cambian dichos parámetros permite que la geometría de una estructura se adapte satisfactoriamente a los requerimientos que imponen las condiciones de carga y restricciones aplicadas dentro de un proceso que se hace más exigente con el paso del tiempo. De esta manera, el proceso de optimización genera geometrías que se adecuan paulatinamente a las condiciones, hasta el punto en que no hay cambio posible que genere un mejor resultado. El modelado con curvas paramétricas produce contornos suaves a la geometría de los modelos, lo cual se traduce en evitar, en la medida de lo posible, la aparición de aristas con cambios bruscos de dirección que puedan actuar como concentradores de esfuerzo o aristas rugosas no deseables. A continuación se describe el algoritmo desarrollado para el método propuesto.

1. La geometría del modelo se define con curvas B-Spline y se indican las restricciones y los casos de carga aplicados al modelo.

2. Se calcula el esfuerzo de von Mises en los nodos por medio de FEA.

3. Se modifica la frontera de la geometría con base en un proceso de remoción o adición de material basada en el nivel de esfuerzo de los nodos en la frontera. La remoción se lleva a cabo en los nodos de bajo nivel de esfuerzo, aplicando vectores de desplazamiento en dirección interior sobre los puntos de control asociados a dichos nodos. Por otra parte, la adición de material se aplica a aquellos nodos cuyo nivel de esfuerzo sea alto o el esfuerzo de von Mises sea mayor al esfuerzo de cedencia del material. En este caso, la dirección del desplazamiento de los puntos de control es exterior.

4. Los pasos 2 y 3 se repiten hasta que no sea posible mejorar el modelo.

Los pasos en la descripción del algoritmo son sencillos de entender; sin embargo, la forma como se modifica la frontera, es decir el paso 3, requiere de especial atención, debido a que el cálculo de los vectores de desplazamiento generados para dicha modificación no es trivial.

 

Modificación de la frontera

La optimización de la geometría del cuerpo se realiza a través de cambios graduales en la frontera del mismo. Los cambios en la geometría emulan un proceso de remoción o adición de material en la frontera del modelo. Mientras que en métodos como ESO, esta remoción o adición de material se lleva a cabo agregando o retirando fragmentos de la geometría, lo que genera fronteras escalonadas y rugosas.

El método propuesto por el autor se realiza aplicando desplazamientos pequeños sobre los nodos que definen la frontera y que muestran un nivel de esfuerzo identificado como bajo o alto.

 

Regiones modificables

Para modelos sometidos a un solo caso de carga, una región modificable (o ineficiente) será aquella que esté compuesta por nodos que cumplan con alguna de las siguientes inecuaciones:

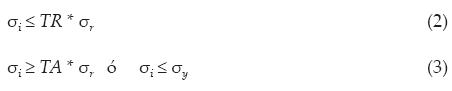
donde

σ₁ es el esfuerzo de von Mises del i-ésimo nodo,

σ_r es un esfuerzo de referencia, por ejemplo el esfuerzo máximo de la estructura,

σ_y es el esfuerzo de cedencia del material, TR y TA son las tasas de remoción y adición de material, respectivamente, también se conocen como parámetros de evolución.

Así, aquellos nodos que satisfagan la inecuación (2) son candidatos a ser modificados emulando remoción de material, mientras que los que cumplan la desigualdad (3) emulan adición. Dicho de otra forma, (2) identifica regiones sub-esforzadas de la frontera y (3) identifica regiones sobre-esforzadas.

Los valores de TR y TA pertenecen al intervalo de 0.0 a 1.0, donde TR < TA, cuya función es definir límites temporales en el nivel de esfuerzo para cada iteración en el proceso de optimización. Estos valores se actualizan cada vez que se alcanza un estado permanente en el proceso, es decir, aquel para el cual no es posible mejorar el modelo (remover o adicionar material) empleando los valores actuales de TR y TA. Así, la actualización de los parámetros se lleva a cabo de acuerdo con:

donde TER y TEA son las tasas evolutivas de remoción y adición, respectivamente y j indica el j-ésimo estado permanente.

En este trabajo, después de hacer pruebas con diferentes valores de los parámetros se establecieron los siguientes valores: TR ≈ 0.01 → 0.1, TA ≈ 0.9 → 0.99, TER ≈ 0.01, TEA ≈ 0.0 → 0.001.

Para problemas en los que existen múltiples casos de carga, las regiones ineficientes deben determinarse comparando el efecto de cada uno de los niveles de esfuerzos obtenidos para cada caso de carga. De esta forma, un nodo será candidato a remoción si lo es para todos los casos de carga, mientras que será candidato a adición si lo es al menos para uno de los casos. A esta manera de considerar los nodos de remoción y adición se le puede englobar en un algoritmo de lógica AND/ OR (Li et al., 1999)

Tomando en cuenta lo anterior, las inecuaciones (2) y (3) cambian de la siguiente forma: si N es el número de casos de carga aplicados en el modelo, para cada nodo i se verifican las siguientes expresiones, donde j representa al caso de carga j-ésimo:

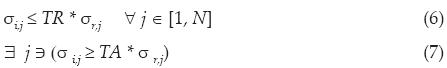
Si para el nodo i se cumple (6), dicho nodo se somete a remoción (lógica AND); si se satisface (7) entonces el nodo sufrirá adición de material (lógica OR).

 

Modificación de los puntos en la frontera

La optimización del modelo o estructura se lleva a cabo por medio de la modificación de su contorno. Ésta se realiza cambiando indirectamente la posición de los nodos de las curvas B-Spline desplazando los puntos de control P_i que las definen.

En general, los diferentes métodos de optimización estructural que trabajan con base en movimientos de la frontera, lo hacen aplicando desplazamientos en dirección perpendicular a la frontera sobre los nodos de la misma (Annicchiarico y Cerrolaza, 2001; Cerrolaza et al., 2000; Mattheck, 1998 y 2006; Cervera, 2005a y 2005b). El problema común de estos es que al tomar en cuenta sólo la dirección perpendicular a la frontera en el nodo a desplazar, no se considera que puedan existir nodos vecinos también susceptibles de modificación. En este sentido, la información importante de la geometría y el estado de esfuerzos en la vecindad del nodo no se toman en cuenta.

En este trabajo se propone utilizar la información de la vecindad de los nodos a modificar aprovechando las propiedades de las curvas B-Spline. En primer lugar, la posición de un nodo C (u_i) en una curva B-Spline de grado p es dependiente de la posición de los puntos de control de acuerdo con (1); sin embargo, en realidad lo es sólo de p +1 puntos de control (Shene, 1998).

Por otra parte, las B-Spline son curvas paramétricas definidas por segmentos. Si m es el número de nodos que definen la curva, entonces existen m - 1 segmentos, cada uno en el intervalo [u_i, u_i+1] y m puntos de control. Además, si cada nodo C (u_i) de la curva coincide con el inicio de un intervalo, entonces los p + 1 puntos de control de los cuales depende la posición del punto son: P¡_{- 1} > P¡> P_i+1 , P_i+2 , .. P_{i+p- 1}. Dado que, en este trabajo se utiliza el valor p = 3, los puntos de control que determinan la posición de C (u_i) son: P_{i - 1} , P_i, P_i+1 , P_i+2 (figura 2).

Lo anterior también se puede apreciar si se estudia el siguiente sistema (8) en el que se muestra la relación entre nodos de la curva, puntos de control y funciones de interpolación correspondientes a una curva B-Spline de 3er grado.

ecuación (8)

o, matricialmente:

Una propiedad importante de las funciones de interpolación es que para todo punto de la curva se cumple (10):

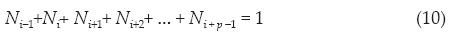
Esta propiedad también puede entenderse como que los puntos de control P_i-1 , P¡ , P_i+1 , P_i+2 , ... , P_{i+p - 1} contribuyen con porcentajes N_i-1 , N¡ , N_i+1 , N¡ +₂ , ... , N_i+1, respectivamente, en la posición del nodo C(u_i) de la curva. De esta manera, un punto de control P_i afecta en porcentajes N_i (u_i-p+1), ..., N_i (u_i-p+2), ..., N_i(u_i), N_i(u_i+1) posición de los nodos C(u_i-p+1), C(u_i-p+2), ... ,C(u_i), C(u_i+1) respectivamente (figura 3). Observe que, en general:

Si se desea modificar la posición del nodo C(u_i) de una curva B-Spline con un desplazamiento 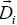, los puntos de control P_i-1 , P_i, P_i+1, P_i+2, ..., P_i+p-1 deben afectarse por los desplazamientos respectivamente. Aún más, si se debe cambiar la posición de los nodos C(u_i) y C(u_i+1) con desplazamientos independientes 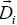y 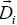+₁ respectivamente, entonces los desplazamientos a calcular serán y 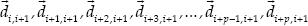, los cuales son arbitrarios e independientes entre sí.

Conjuntos similares de vectores de desplazamientos se generan para cada uno de los nodos, donde el primer subíndice corresponde al punto de control sobre el cual se deben aplicar y el segundo al nodo sobre la curva para el cual fue generado. Si se aíslan los vectores correspondientes a un punto de control P_i se obtiene el conjunto .

Es evidente que el vector de desplazamiento equivalente necesario para llevar a cabo las modificaciones correspondientes a cada uno de los nodos dependientes de la posición de P_i no es igual a la suma de los vectores asociados, es decir:

Aparentemente, para determinar los desplazamientos de cada punto de control bastaría con resolver la ecuación (13)

Sin embargo, esta ecuación no considera que modificar arbitrariamente la posición de los nodos, provoca que los valores de los parámetros u sobre dichos nodos (y, por lo tanto, los intervalos de definición de los segmentos de la curva) cambien al mismo tiempo que los valores de las funciones de interpolación. Hay que recordar que los valores de los parámetros u son resultado de una relación geométrica entre los nodos C(u). Así, resolver la ecuación (13), sin tomar en cuenta tales circunstancias, produciría puntos de control que representarían una curva B-Spline diferente a la original. Adicional-mente, si los cambios en los parámetros y los intervalos son demasiado grandes es muy probable que la nueva curva sufra distorsiones indeseables para la optimización del modelo (Cervera, 2005a; Yang, 2004).

En el método de optimización empleado en este trabajo es regla general que en cada iteración se modifique la posición de varios puntos de la frontera a la vez. El cambio de posición está directamente relacionado con el nivel de esfuerzo de dichos puntos a través de las ecuaciones (2) y (3), si se trata de un problema con un solo caso de carga, o de las ecuaciones (6) y (7), si existen múltiples casos de carga. A su vez, los cambios deben llevarse a cabo desplazando los puntos de control de la curva, cuyo cálculo, como ya fue descrito, no es trivial. Los vectores de desplazamiento de los puntos de control se calculan de forma que, por una parte, se asegure que la magnitud de los desplazamientos no genere distorsiones indeseables y, por la otra, la dirección de los mismos considere la información de la vecindad de cada punto.

 

Cálculo de la magnitud y la dirección de los desplazamientos

Para asegurar que no se generen distorsiones en la frontera de la estructura y obtener una velocidad moderada en el proceso de optimización, la magnitud de los desplazamientos de todos los puntos de control se restringe, de modo que

donde esize es el tamaño promedio de los elementos finitos en la frontera, y f es un factor de modificación que permite controlar la velocidad con la que cambia la geometría, cuyo valor es menor o igual a la unidad.

Sólo los nodos C(u) que satisfagan las ecuaciones (2) y (3) o (6) y (7) deben considerarse para el cálculo de los desplazamientos de los puntos de control. Para cada nodo C(u) se calcula un vector de desplazamiento 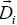de acuerdo con las siguientes reglas:

□ Si C(w) satisface (2) o (3), entonces la magnitud es respectivamente:

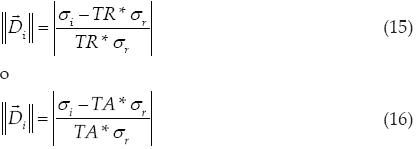
□ Si C(u) satisface (6) o (7), entonces la magnitud es respectivamente:

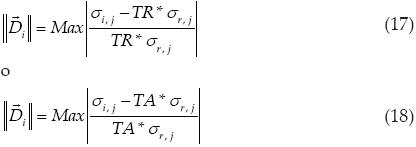
donde j = 1, 2, ... , N, indica cada uno de los casos de carga.

Por otro lado, si es el vector unitario normal exterior a la frontera en el nodo C(u_i), la dirección de 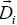es:

Esto implica que en regiones de bajo nivel de esfuerzo se remueva material, mientras que en las de alto nivel de esfuerzo se ejecute adición de material. Los vectores son la base para el cálculo del vector d_i de cada punto de control P_i. Para desplazar a P_i deben tomarse en cuenta los desplazamientos de los nodos C(u_i-p+1), C(u_i-p+2), ... , C(u_i), C(u_i+1) es decir, . A su vez, a estos nodos les corresponden, por la influencia de P_i , respectivamente, los valores de las funciones de interpolación N_i(u_{i - p + 1}), N_i (u_{i- p + 2}), ... , N_i (u_i), N_i(u_i+1). Estos últimos representan el porcentaje de participación del punto de control P_i en la posición de cada uno de los nodos mencionados. Dicho de otra form a, si el punto de control P_i debe desplazarse, el vector debe tomar en cuenta la participación del punto de control sobre los nodos correspondientes de la curva.

El procedimiento propuesto para el cálculo del vector emplea los valores N_i(u_i-p+1), N_i(u_i-p+2), ... , N_i(u_i), N_i(u_¡+1) como factores de ponderación para combinar los vectores de acuerdo con:

donde es la suma vectorial ponderada de los desplazamientos de los nodos que están asociados al punto de control P_i. El cálculo de es necesario para determinar la dirección del desplazamiento del punto de control P_i, de forma que tome en cuenta, en su justa medida, la dirección de desplazamiento de los nodos sobre la frontera (figura 4).

Por otra parte, si m es el número de nodos en la frontera y q es el subíndice del parámetro u de la función de interpolación que cumple con (23), entonces el valor de será el dado por (24).

En otras palabras, la magnitud del desplazamiento del punto de control P_i es igual al valor normalizado del desplazamiento del nodo sobre el cual P_i tiene mayor efecto (es decir, C(u_q)), multiplicado por el tamaño promedio de la malla (esize) y por el factor de modificación (f). La idea principal de esta forma de calcular el vector es que, por una parte, en el cálculo de la dirección se utiliza la información de la vecindad de los nodos en la frontera y no sólo la de un nodo aislado; por la otra, en el cálculo de la magnitud se favorece el desplazamiento de los nodos más influenciados por el punto de control.

 

Criterio de paro

En los métodos de optimización existen diferentes criterios de paro, los cuales dependen de las variables de diseño y las características que se estén considerando. Una característica deseable de un diseño es la homogeneidad del nivel de esfuerzos. El nivel de esfuerzos mide qué tan alejado del valor de referencia (esfuerzos máximo, promedio, de fluencia, etcétera) está el esfuerzo de cada uno de los elementos finitos que componen al cuerpo. El homogeneizarlo significa que durante la optimización su valor converge. En el caso ideal el nivel de esfuerzos convergería a cero, lo cual significa que todo el modelo experimenta el esfuerzo de referencia. Cuando el esfuerzo es homogéneo se dice que se tiene un diseño completamente esforzado. En la realidad esto es casi imposible debido a las condiciones de frontera, teniendo así niveles homogéneos de esfuerzo mayores a cero.

El nivel de esfuerzos Na de todo el modelo se calcula como

La convergencia del nivel de esfuerzos se da cuando (26) se satisface para n iteraciones consecutivas.

Los valores de n y tol deben fijarse de forma que se superen los óptimos locales en los casos en que el o_r, debido a que la magnitud de las fuerzas aplicadas, no alcance un valor límite, por ejemplo, el esfuerzo de fluencia del material empleado para diseño en el rango elástico. Para el problema del cuerpo suspendido abordado en este trabajo, se definieron n =5 y tol = 10^-4, donde el segundo es el recomendado por Cervera en 2005a y 2005b. El uso de valores de tol menores, provocaría que la homogeneidad del nivel de esfuerzos fuera menor, mientras que valores mayores implicarían una mejor homogeneidad; sin embargo, el tiempo de cómputo se incrementaría considerablemente.

 

Índice de desempeño

La pregunta inherente a cualquier método de optimización empleado en el diseño óptimo de estructuras es: ¿la geometría generada por el método, realmente es la óptima para las condiciones de cargas y las restricciones dadas? Aunque existen algunas soluciones estándar para algunos problemas específicos (como las desarrolladas por Michell (1904), Hemp (1973), Rozvany (1995), entre otros), el espectro de problemas que pueden plantearse es ilimitado, por lo que resulta imposible encontrar una solución estándar para cada uno de ellos. Más aún, si las soluciones estándar de un problema particular son comparadas entre sí, se llega a la conclusión de que son similares más no iguales, ya que cada una de ellas tiene una fuerte dependencia con los planteamientos, suposiciones, consideraciones y objetivos empleados en la formulación de los métodos que las produjeron (figura 5).

Por estas razones, es necesaria una medida que cuantifique qué tan bueno y qué tan cercano a un resultado óptimo está la estructura generada, independientemente del método utilizado para ello. A esta medida se le llama índice de desempeño.

 

Cálculo del índice de desempeño

El procedimiento de cálculo del índice de desempeño usado en este trabajo es una adaptación del procedimiento desarrollado por Querin (1977). Las dos características principales del PI son: que es un número que engloba las características completas de la solución y que es adimensional. Dado que el método propuesto se basa en el nivel de esfuerzos, el PI se calcula como una medida del efecto sufrido por el modelo o estructura y la causa que lo provoca. Dicho de otra manera, PI es una relación del estado de esfuerzos de la estructura entre el sistema de cargas aplicado, esto es

donde

σ_e y V_e son el esfuerzo de von Mises y el volumen del e-ésimo elemento finito,

NE es el número de elementos finitos en la malla,

F es la resultante del sistema de fuerzas aplicado y

L es una longitud nominal de la geometría.

Si el problema de optimización implica la aplicación de varios casos de carga, entonces (27) debe adaptarse

donde LC es el número de casos de carga aplicados y, F_j es la fuerza resultante del j-ésimo caso de carga.

 

Interpretación de PI

Querin (1997), señala que el mejor modelo o estructura optimizado es fácilmente identificado si se monitorea el valor de PI durante el proceso de optimización y se elige aquella con el menor valor de PI. Una característica fundamental de PI es que, durante el proceso de optimización, mientras una estructura evoluciona hacia la estructura óptima constituida por una geometría continua, el valor de PI se decrementa.

Geometría continua debe entenderse como aquella que no presenta huecos, cavidades o concavidades importantes.

En general, cuando la geometría deja de ser continua, por ejemplo, cuando se crean huecos, el valor de PI se eleva abruptamente. Dado que en este trabajo sólo se optimiza la estructura modificando su frontera, este efecto ocurrirá durante el proceso de optimización, cuando la frontera presente concavidades de consideración o regiones de curvatura elevada. Lo anterior es de esperarse, pues los huecos, concavidades, etcétera actúan como concentradores de esfuerzo, por lo que (27) y (28) en sus numeradores contendrán valores que se incrementan respecto a los correspondientes de una geometría continua.

Se pueden hacer algunas observaciones en cuanto al significado de PI. Si bien el óptimo global es la estructura que muestre el menor valor de PI, los resultados obtenidos por Querin (1997) muestran que pueden obtenerse varios óptimos locales durante el proceso de optimización. El óptimo global, en general, es una estructura con geometría continua; sin embargo, si el proceso de optimización se lleva a cabo más allá del óptimo global, la geometría evoluciona a una que deja de ser continua, pero el PI continúa cambiando y mostrando mínimos locales que corresponden a resultados óptimos que también pueden llamarse locales. En este sentido, PI permite identificar más de un óptimo durante el proceso, es decir, un óptimo global y un conjunto de óptimos locales, cada uno para las características geométricas del modelo en las iteraciones identificadas.

La figura 6 corresponde al diseño de un caso de las estructuras de Michell. De a) se identifica como óptimo global la estructura obtenida en la iteración 21. Al continuar con el proceso de optimización aparecen óptimos locales para las iteraciones 28 y 55, los cuales se identifican en a) como los puntos que corresponden a mínimos locales. Como se explicó, estos óptimos locales están caracterizados por la aparición de cavidades en la estructura.

A diferencia de lo realizado por Querin, el método y el algoritmo empleados en este trabajo, únicamente trabajan sobre el contorno de los modelos a optimizar. Por lo tanto, los óptimos tanto global como locales se caracterizan por la aparición de concavidades de curvatura elevada que actúan como concentradores de esfuerzos. A pesar de esta diferencia, la información arrojada por el historial del índice de desempeño permite identificar los óptimos del proceso. Hay que mencionar que la elección del óptimo más útil entre el global y los locales depende de varios factores, tales como facilidad de fabricación, material de fabricación, peso, estética, entre otros.

 

Diseño de la geometría de un fruto

Las formas que la naturaleza ha dado a los frutos son bien conocidas por todo mundo, aunque no todos saben el por qué de éstas. Querin (1997), por medio del método ESO, demostró que la forma de algunos frutos, como la cereza o la manzana, surge de un proceso de optimización natural que depende fundamentalmente del nivel de esfuerzo superficial experimentado por el fruto, debido a fuerzas de cuerpo. En este apartado se corrobora lo comprobado por Querin, aplicando la metodología de optimización descrita.

El dominio de diseño representa un cuerpo suspendido sujeto a la acción de fuerzas de cuerpo debidas a la gravedad (densidad de 2700 kg/m³ y g = 9.81 m/s² en dirección vertical negativa), con módulo de Young de 70 GPa y coeficiente de Poisson de 0.33, el cual está contenido en un cuadrado de 100 mm por lado, (figura 7a). Es importante señalar que las propiedades del material empleado para la optimización no corresponden a las de los frutos en la naturaleza. Sin embargo, no es necesario que correspondan debido a que, como es sabido, la distribución de esfuerzos en un cuerpo homogéneo es función sólo de la geometría y las condiciones de frontera (fuerzas y restricciones) aplicadas, de tal suerte que la forma óptima obtenida es válida para el material propio de los frutos.

En la figura 7b se observa la distribución de esfuerzos de von Mises inicial en el dominio de diseño, obtenida usando un tamaño promedio de elemento de 2 mm, resultando en una malla de 50x50 elementos finitos, donde los esfuerzos máximo y promedio son: 65.87 kPa y 2.99 kPa, respectivamente. Debe apuntarse que el tamaño de malla elegido genera una distribución de esfuerzos sin cambios abruptos, como se observa en las figuras 7b y 10. Tamaños de malla más pequeños no aportarían mayor calidad en la distribución de esfuerzos y sí requerirían mucho mayor tiempo de cálculo.

Se utilizaron los siguientes valores iniciales para los parámetros de optimización: TR = 0.5, TA = 0.9, TRE = 0.015, TAE = 0.001. Durante el proceso se consideraron las líneas L1, L2 y L4 como fijas, evolucionando únicamente la L3, la cual modela el cuerpo del fruto. Los cambios en el área y los esfuerzos máximo y promedio de von Mises generados durante la optimización se pueden apreciar en los gráficos de la figura 8.

En la figura 9 se muestran el comportamiento del nivel de esfuerzos y del índice de desempeño. En el primer caso, se observa que el nivel de esfuerzos tiene una tendencia a disminuir, presentando incrementos repentinos, pero que cada vez son de menor magnitud. La convergencia del nivel de esfuerzos se alcanza después de las 90 iteraciones, como lo indica la figura, donde en la iteración 97 se alcanza el criterio de paro.

Según el gráfico del índice de desempeño, se alcanza una geometría óptima en la iteración 39. Sin embargo, el índice continúa disminuyendo paulatinamente con la cualidad de que las geometrías correspondientes son similares entre sí cambiando prácticamente sólo en su tamaño.

En la iteración 61 se presenta otro cambio en la tendencia del índice de desempeño, así como en la forma de las geometrías resultantes.

Observando los gráficos de la figura 10 se pueden identificar formas bien conocidas de frutos. Estos resultados, igual que el de Querin (figura 11), indican que la forma que la naturaleza ha dado a muchos de los frutos que se conocen se define con base en el nivel de esfuerzos de las mismas. Cabe señalar que, aunque las geometrías producidas por ambos métodos son muy similares, el método propuesto por el autor requiere mucho menos recursos de cómputo. Mientras que Querin utilizó una malla de 100x100 elementos finitos, los resultados mostrados en la figura 10 requirieron únicamente una malla de 50x50, una cuarta parte de la cantidad de elementos finitos usada por el primero. Lo anterior es una de las virtudes intrínsecas al modelado paramétrico de la geometría. Hablando de la similitud de los resultados de uno y otro método, hay que resaltar que, tal como fue mostrado en la comparación entre métodos de la figura 5, las diferencias entre la forma de tratar a las geometrías provocan que los resultados no sean exactamente iguales; sin embargo, ambos resultados son válidos en el contexto de las características propias de los métodos.

En el caso de ESO se trata a la geometría como formada por pequeños bloques, los cuales son eliminados o añadidos, mientras que en el método utilizado en este trabajo la geometría se concibe como un contorno formado por curvas paramétricas. Por lo anterior, difícilmente los resultados de los diferentes métodos serán idénticos, pero tendrán enormes similitudes entre sí.

 

Conclusiones

Con los resultados descritos en el apartado anterior se corrobora que la forma de un fruto es el resultado de un proceso de optimización de forma, en el cual el nivel de esfuerzos superficiales es homogéneo. Tanto los resultados obtenidos por Querin (1997) como los mostrados en este trabajo lo demuestran. No obstante, el método descrito en este trabajo no requiere una malla de elementos finitos tan fina, lo cual es una ventaja sobre el método ESO en cuanto a recursos de cómputo se refiere. La modificación de la frontera basada en la información de los puntos en la frontera, así como de su vecindad produce resultados adecuados, lo cual demuestra su funcionalidad y factibilidad.

 

Referencias

Annicchiarico W., Cerrolaza M. Structural Shape Optimization 3D Finite-Element Models Based on Genetic Algorithms and Geometric Modeling. Finite Elements in Analysis and Design, volumen 37 (número 5), 2001: 403-415.         [ Links ]

Cerrolaza M., Annicchiarico W. et al. Optimization of 2D Boundary Element Models Using B-Splines and Genetic Algorithms. Engineering Analysis with Boundary Elements, volumen 24 (número 5), 2000: 427-440.         [ Links ]

Cervera E., Trevelyan J. Evolutionary Structural Optimisation Based on Boundary Representation of NURBS: Part I: 2D Algorithms. Computers & Structures, volumen 83 (números 23-24), 2005a: 1902-1916.         [ Links ]

Cervera E., Trevelyan J. Evolutionary Structural Optimisation Based on Boundary Representation of NURBS: Part II: 3D Algorithms. Computers & Structures, volumen 83 (números 23-24), 2005b: 1917-1929.         [ Links ]

Hemp W.S. Optimum Structures, Claredon Press, Oxford, 1973.         [ Links ]

Li Q., Steven G.P., Xie Y.M. On Equivalence between Stress Criterion and Stiffness Criterion in Evolutionary Structural Optimization. Structural Multidisciplinary Optimisation, volumen 18 (número 1), 1999: 67-73.         [ Links ]

Liang Q.Q., Xie Y.M. Optimal Selection of Topologies for the Minimum-Weight Design of Continuum Structures with Stress Constraints. Proc. Inst. of Mech. Engrs., volumen 213, Part C, 1998.         [ Links ]

Mattheck C., Burkhardt S. A New Method of Structural Shape Optimization Based on Biological Growth. International Journal of Fatigue, volumen 12 (número 3), 1990: 185-90.         [ Links ]

Mattheck C. Design in Nature- Learning from Trees, 1a ed., Alemania, Springer Verlag, 1998.         [ Links ]

Mattheck C. Teacher Tree: The Evolution of Notch Shape Optimization from Complex to Simple. Enginering Fracture Mechanics, volumen 73 (número 12), 2006:1732-1742.         [ Links ]

Maute K., Ramm E. Adaptative Topology Optimization. Structural and Multidisciplinary Optimizaction, volumen 10 (número 2), 1995: 100-112.         [ Links ]

Michell A.G.M. The Limits of Economy of Material in Frame Structures. Philosophical Magazine, volumen 8, 1904: 589-597.         [ Links ] Querin O. Evolutionary Structural Optimisation: Stress Based Formulation and Implementation, tesis (Ph.D Dissertation), Australia, Department of Aeronautical Engineering, University of Sydney, Abril 1997.         [ Links ]

Ramm E. et al. Adaptative Topology and Shape Optimization, Computational Mechanics-New Trends and Applications, CIMNE, Barcelona, Spain, 1998.         [ Links ]

Rozvany G.I. et al. Layout Optimization of Structures. Appl. Mech. Rev., volumen 48 (número 2), 1995: 41-119.         [ Links ]

Shene C. Introduction to Computing with Geometry [en línea] [fecha de consulta: julio 1 de 1998], Course Notes. Disponible en: http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/        [ Links ]

Sethian J.A., Wiegmann A. Structural Boundary Design via Level Set and Immersed Interface Methods. J. Comp. Phys., volumen 163 (número 2), septiembre 2000: 489-528.         [ Links ]

Steven G.P., Xie Y.M. Evolutionary Structural Optimization with FEA. Computational Mechanics, volumen 1, 1993: 27-34.         [ Links ]

Velázquez-Villegas F. Optimización estructural evolutiva: Optimización de forma basada en modelado paramétrico y reglas evolutivas, tesis (doctorado en ingeniería), México DF, Facultad de Ingeniería, Universidad Nacional Autónoma de México, Octubre 2009.         [ Links ]

Velázquez-Villegas F., Santillán-Gutiérrez S.D. Optimización de forma de modelos paramétricos bidimensionales basada en ponderación geométrica y reglas evolutivas. Rev. internacional de métodos numéricos para cálculo y diseño en ingeniería, volumen 28 (número 3), 2012: 135-141.         [ Links ]

Xie Y.M., Steven G.P. Evolutionary Structural Optimization (ESO), 1a ed., Londres, Springer, 1997.         [ Links ]

Yang H. et al. Control Point Adjustment for B-Spline Curve Approximation. Cumputer-Aided Design, volumen 36 (número 7), 2004: 639-652.         [ Links ]

 

Semblanza de los autores

Fernando Velázquez-Villegas. Es doctor en ingeniería y profesor de tiempo completo de la carrera de ingeniería mecánica en la Facultad de Ingeniería de la UNAM. Su línea de investigación está relacionada con técnicas de optimización aplicadas al diseño mecánico y estructural. Ha dirigido tesis de licenciatura y posgrado en las mismas áreas. Coordinador y colaborador en proyectos de desarrollo tecnológico en el Centro de Diseño Mecánico e Innovación Tecnológica (CDMIT) y en Centro de Alta Tecnología (CAT). Líder del Grupo de Diseño Mecánico Óptimo (GDMO) de la Facultad de Ingeniería.

Saúl Daniel Santillán-Gutiérrez. Es doctor en ingeniería de diseño por Loughbo-rough University of Technology en Inglaterra. Ha dirigido tesis de licenciatura en el área de diseño mecánico, así como proyectos de investigación y desarrollo tecnológico. Es miembro de la Sociedad de Exalumnos de la Facultad de Ingeniería de la UNAM (SEFI), de la American Society of Mechanical Engineers (ASME), de la Asociación de Ingenieros Universitarios Mecánicos Electricistas (AIUME), así como miembro fundador de la Sociedad Mexicana de Ingenieros Mecánicos. Imparte cursos a niveles licenciatura y maestría en el área de desarrollo de productos, inteligencia artificial y métodos de diseño. Actualmente es jefe de la Unidad de Desarrollo Tecnológico Querétaro.