Analysis of Equivalent Circuits for Cells: A Fractional Calculus Approach

 

Análisis de circuitos equivalentes para células: un enfoque de cálculo fraccionario

 

Gómez-Aguilar F.¹ Rosales-García J.² Guía-Calderón M.³ Bernal-Alvarado J.⁴

 

¹ Departamento de Ingeniería Física División de Ciencias e Ingenierías Campus León Universidad de Guanajuato Correo: jfga@fisica.ugto.mx

² Departamento de Ingeniería Eléctrica División de Ingenierías Campus Irapuato Salamanca Universidad de Guanajuato Correo: rosales@salamanca.ugto.mx

³ Departamento de Ingeniería Eléctrica División de Ingenierías Campus Irapuato Salamanca Universidad de Guanajuato Correo: guia@salamanca.ugto.mx

⁴ Departamento de Ingeniería Física División de Ciencias e Ingenierías Campus León Universidad de Guanajuato Correo: bernal@fisica.ugto.mx

 

Información del artículo: recibido: abril de 2011
Reevaluado: agosto de 2011
Aceptado: agosto de 2011

 

Abstract

Fractional order systems are considered by many mathematicians the systems of the XXI century. The reason is that nature has proved to be best described in terms of systems composed of fractional order derivatives. This emerging area of research is slowly gaining more strength in engineering, biochemistry, medicine, biophysics, among others. This paper presents an analysis in the frequency domain equivalent of cellular systems described by equations of integer and fractional order; it also carries out an analysis in time domain in order to display the memory capacity of fractional systems. It presents the fractional differential equations equivalent models and simulations comparing integer and fractional order.

Keywords: electrical impedance, fractional calculus, fractional capacitor.

 

Resumen

Los sistemas de orden fraccionario son considerados por muchos matemáticos como los sistemas del siglo XXI. Esto se debe a que se ha visto que la naturaleza se describe mejor en términos de sistemas compuestos de derivadas de orden fraccionario. Esta área de investigación emergente está ganando más fuerza en ingeniería, bioquímica, medicina, biofísica, entre otros. Este artículo presenta un análisis en el dominio de la frecuencia de los sistemas celulares descrito por las ecuaciones de orden entero y de orden fraccionario, también lleva a cabo un análisis en el dominio del tiempo con el fin de mostrar la capacidad de memoria de los sistemas fraccionarios. Se presentan las ecuaciones diferenciales fraccionarias equivalentes a los modelos descritos y las simulaciones que comparan el orden entero y fraccionario.

Descriptores: impedancia eléctrica, cálculo fraccionario, capacitor fraccionario.

 

Introduction

Although the mathematical foundation of fractional calculus was established over 200 years ago, remains a subject quite new to mathematicians. The basic idea lies in considering derivatives and integrals of arbitrary order. The calculation of fractional order had not been used in engineering because of its complexity and apparent satisfactory description of the phenomena with the calculation of integer order (regular), together with the fact that it has no physical interpretation and geometric totally acceptable (Machado et al., 2003). However, due to the fact that most accurately represents some natural behaviors related to different areas of engineering, has been used more frequently. Some applications are in bioengineering (Magin and Ovadia, 2008), electromagnetism (Machado et al., 2006) among others. The advantage of using fractional order systems compared with systems of integer order (ordinary) is that the former has infinite memory, while others have finite memory.

The fractional computational complexity lies in the many definitions that describe it. Some common definitions found in (Podlubny, 1994; Gutiérrez et al., 2010). To analyze the dynamic behavior of a link fractancia we need a proper definition of fractional derivative associated to a representation in the frequency domain. The need to obtain ordinary differential equations of fractional order to resolve problems of initial value suggests that a good definition of fractional derivative is that proposed by Caputo (Podlubny et al., 1994), which is defined by:

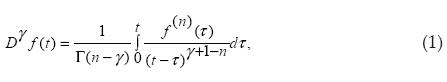
where n - 1 < y < n (n is N), and f ⁽ⁿ⁾(τ) represents the derivative of order n, real function evaluated in t. Working with this definition is important due to its ability to be implemented numerically (Diethelm et al., 2005). The Caputo derivative has the following property: if f (t) is a constant, then its derivative is zero which does not happen with other representations. Another very important feature in the form of Caputo fractional derivative is that its Laplace transform is:

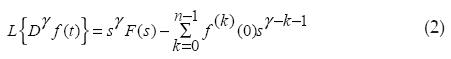
From equation (2), we can see that the representation of the Caputo derivative in Laplace domain using the initial conditions f^(k)(0) where k is an integer. If the initial conditions are zero, this reduces to:

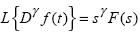
This is consistent with the usual definition of the Laplace transform when y is an integer. In general, a fractional order differential equation has the form

where y_k > y_k-1 and a_k are any real numbers, g(t) can be seen as the source of a dynamic system. The inverse transform 0 < y < 1 requires the introduction of a special function. The Mittag-Leffler function, where Γ is the gamma function defined as

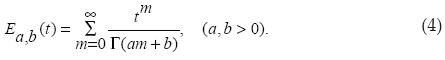
from (4) if a = 1, b = 1, then we obtain the expression E_1,1(t) = e^t. Therefore, the Mittag-Leffler function includes the exponential as a special case.

Bode diagram provides a graphic representation of the magnitude and phase versus frequency of the transfer function, which we have 2 graphs, for magnitude and phase (Dorf, 2000). The Nyquist diagram is a polar plot of the magnitude of the impedance and phase angle, its usefulness is related to the stability analysis of the circuits studied with a model in complex variable impedance of the sample (Dorf, 2000). The Cole impedance model was postulated in its final form by Kenneth Cole in 1940 (Cole, 1940), which is based on replacing the ideal capacitor in the Debye model (Deb-ye, 1945) for a general element called constant phase (EFC). The idea of introducing an EFC came after reviewing a number of phenomena in electrochemistry and tissue and cell suspensions, and by measuring the impedance in the complex plane (Nyquist diagram) were arches whose geometries showed a lag in center, and observed that these arcs are proposing best fit constant phase elements. The analysis of the Cole impedance model requires three things: an equivalent circuit, the development of their corresponding equations, and the simulation which gives the complex impedance behavior. The impedance model was developed in 1930 by obtaining the complete mathematical equation (Cole, 1940).

The following section describes the application of the above scheme to modeling biological systems using equivalent circuits. The mathematical model is obtained with ordinary derivatives of integer and fractional order and analyzes the behavior of some of its state variables.

The electrical impedance spectroscopy applied to the characterization of biological materials is called bioimpedance. The characteristics of biological tissues and organisms can be measured through various methods, based on the physical properties of the cells and their components, or from the collection of parameters associated with the cell and cellular activity. Of all these methods, bioimpedance focuses on the extent of the passive electrical characteristics of organisms, tissues and biological materials in general.

The most simple but not simple to measure are the cell culture and fermentation processes, which have highlighted the need to measure the concentration of biomass. Moreover, the advancement of these techniques has allowed their use for non-invasive measurements of living tissues.

These techniques are intended to improve the diagnosis of some diseases and to determine tissue damage while avoiding aggressive testing of damaged tissues. Finally, you can determine the global characteristics of the whole human body (body composition). When determining the impedance by applying a variable frequency current to a biological material, it behaves differently depending on the frequency due to the structure of the cell. This different behavior is often reflected in a change in the impedance spectrum of the whole cell.

The variation of impedance, called relaxation, occurs in some frequencies. In particular the relaxation gives us information about the parameters of interest; it is the so-called f> relaxation. The electrical behavior of cell suspensions or tissues in the region of the f> relaxation will help us to obtain a lumped electrical model representing the different electrical conduction phenomena that occur in it. To determine the parameters of this model it is necessary to accurately measure the impedance with at least two frequencies, before and after relaxation.

If we tried to characterize tissue, we usually obtained impedance spectrum frequency of several samples, from 8 to 30 spread over 3 or more decades, depending on the application.

A measurement system used must have a resolution of about 0.1% and a frequency range up to 20 MHz, making it expensive equipment. One solution is to restrict the number of measures and their scope, and adjust to models that allow us to approach similar performance curves of the material impedance spectrum (Cole-Cole model). So instead of determining, for example, the estimate of biomass growth from low and high-frequency measurements, what needs to be done is to measure the impedance in a frequency sweep with the maximum frequency limited by technology used to approximate the full spectrum with the Cole-Cole model, whose parameters could lead to the estimator.

The bioimpedance measuring method is based on the injection of an alternating electrical current of a very small intensity in the human body to be measured in tissue or cell suspension. This voltage produces a voltage drop that is greater and greater in the electrical impedance of the material.

The team gets the value of the impedance from the measurement of the current amplitude, the voltage amplitude and the phase difference between voltage and current. The impedance Z, represents the opposite biological materials that show the passage of an alternating electrical current.

This can be decomposed into two measurable components: resistance, determined by the flow of current through intra- and extra-cellular electrolyte solutions, and phase, determined by the dielectric properties of tissues, or by the temporary accumulation of charges on cell membranes or other interfaces immersed in the electrolyte solution, structures that act as capacitors to the passage of current. For bioimpedance the measure is based on the principle that biological tissues behave as conductors in varying degrees of electric current and/or dielectric (insulation) depending on their composition.

 

Cole-Cole model

The simplest mathematical model for describing the behavior of biological tissues is the model of Cole-Cole, comprising a resistance circuit (R_p) with a capacitor (C_p), in parallel with a series resistance (R_s); in general, it reflects the electrical resistance of the interface sample-electrode and maintains a value, negligible with respect to (R_p), n is the order of the power that best fits the model obtained. Using the algebraic representation of the circuit we can say it represents the total impedance as:

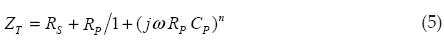
This model allows the characterization of tissue impedance values measured with the Cole model parameters and the values of the components of circuit models, (Casona et al., 1999).

 

Fractional equations Cole-Cole model

Figure 1 shows the equivalent circuit of the Cole-Cole model, where R_s = 0.3, C = 0.6, and R_p = 0.6, all per unit (pu). To determine the equivalent equations, the impedance is calcuated, which is given by the following formula in the complex frequency domain.

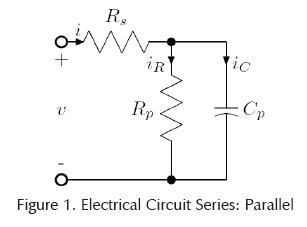
Applying Kirchhoff laws to the circuit of Figure 1, we have:

Before applying the Laplace transform to (7) and (8) we must make the following considerations:

Applying the definition of fractional derivative (Pod-lubny et al., 1994), we have:

Substituting (11) and (12) into (8), we obtain:

Applying the Laplace transform to (13) and (14) we obtain:

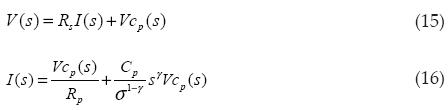
Finally from (15) and (16) we have:

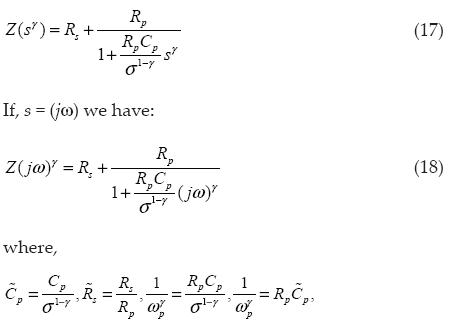
which is the capacitance dispersion. Including this variable and rearranging (18), we have:

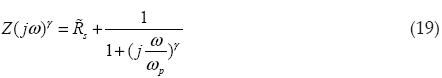
which is the impedance of the Cole-Cole model.

 

Bioimpedance: Application as cell suspensions

The electrical impedance spectroscopy applied to the characterization of biological materials is called bioim-pedance. The characteristics of biological tissues and organisms can be measured through various methods, based on the physical properties of the cells and their components or from the collection of parameters associated with the cell and cellular activity. To determine the impedance by applying a variable frequency current to a biological material has a different behavior depending on the frequency, because of the cell structure. This different behavior is often reflected in a change in the impedance spectrum of the whole cell (Cole, 1941). The biological material is composed of cells in extracellular ion. The cells can be seen simply as an insulating membrane characteristic, called cytoplasmatic membrane; the surrounding of the intracellular fluid is also ionic. The membrane is what gives the dielectric properties of the cell. In addition, changes in ionic permeability of the membrane also cause changes in impedance. Figure 2, shows the equivalent circuit of the cell suspension. Where there is a resistance in parallel, which corresponds to the extracellular medium and impedance that models the cell. This is modeled by a capacitor (C₁) representing the membrane and a resistance that models the intracellular environment (R₂). Where R₁ = 0.2, C₁ = 0.3, and R₂ = 0.4, all per unit (pu). The source is given by u = δ(f) volts.

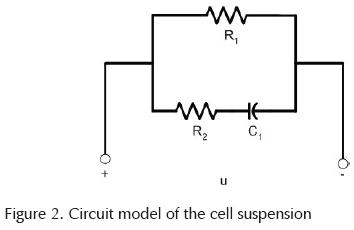
The equation describing the circuit is in terms of the voltage capacitor. Applying Laplace transform with zero initial conditions, we have

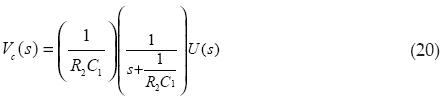
For the equation of fractional order, applying Laplace with zero initial conditions, we have

 

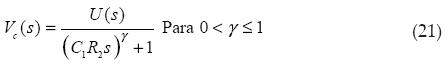
Getting the fractional electric model of the membrane of a cell in terms of the elements of Cole

Figure 3 shows the electrical equivalent circuit of a cell membrane; to determine the equivalent equations, we calculate the impedance, given by the following formula in the complex frequency domain:

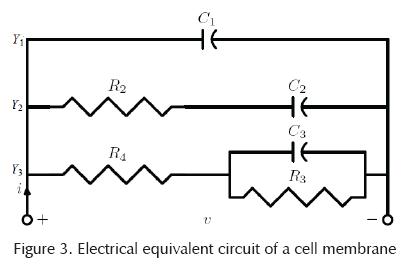
Based on the circuit in Figure 3, we have the following admittances in the Laplace domain:

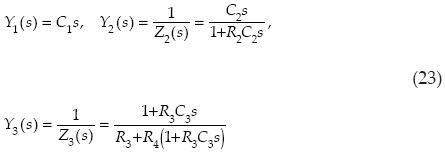
Defining

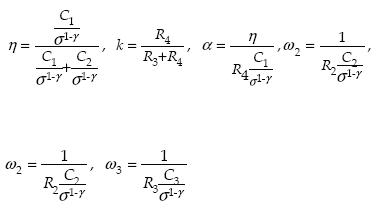
The total circuit admittance is

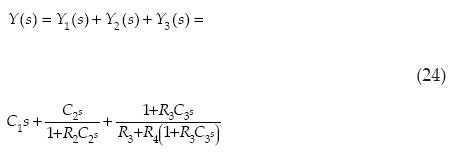
Applying the definition of fractional derivative to (24), the impedance of the system is

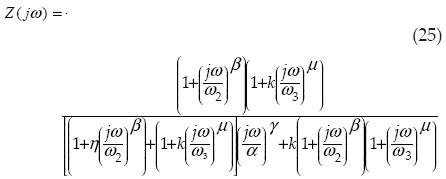
where, s = (jω), equation (25) is the Cole impedance model for the membrane of a cell.

 

Results

All simulations used MATLAB 6.5. Figure 4 shows the simulation for y = 0.95, we can see in Figure 4 and the semicircle described by the Full Nyquist plot (real and imaginary parts for -∞ < ω < ∞) fails to occur due to the fractional power of the Cole model itself. This figure also shows the Bode plot (frequency response).

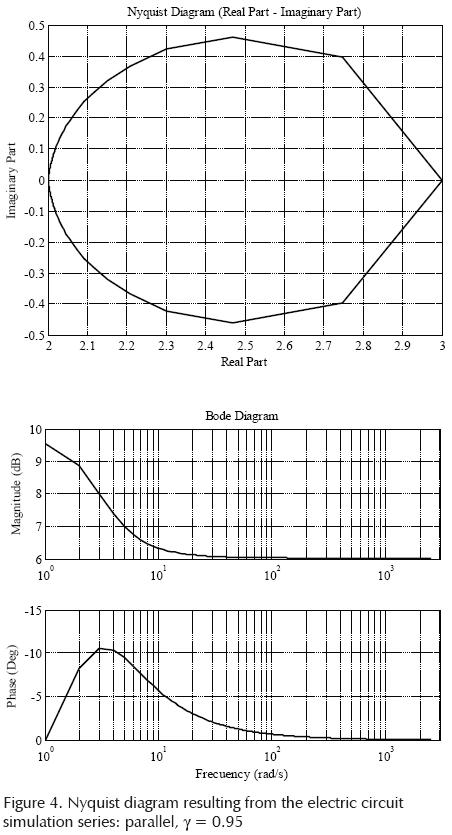
The simulation time was 4.516000 seconds on a computer using Intel Core 2 Duo, 1.8 GHz, 2.99 GB of RAM.

Applying the inverse Laplace transform to (20) and the fractional inverse Laplace transform to (21) we obtain the Mittag-Leffler function with which to perform the analysis in time domain. From Figure 5, we can see that with y < 1, in this case y = 0.8, we note that the function resulting from the fractional model has dropped to 8% of its initial value while the function resulting from the integer model has fallen to 0.6 % of its initial value which allows to observe the response due to the longer fractional model, we calculated the value of the fractional model response for 20 τ(2.4 sec) and reached a value of almost 2% of its final value However, for higher values of time, the response began to oscillate, from which we can deduced that the fractional model has an infinite memory.

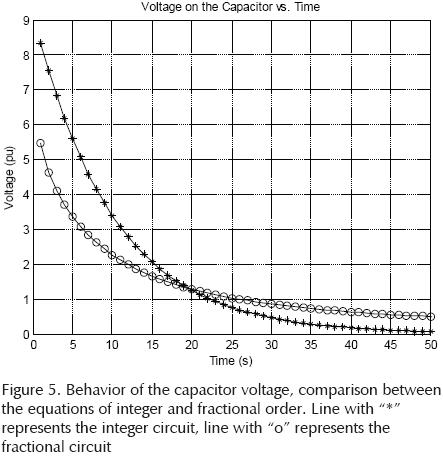
Equation (26) and (27), represent the equation of integer and fractional order, respectively.

where τ = R₂, C₁ = 0.12, y = 0.8, in equation (21) E_y,1 is the Mittag-Leffler function.

The transfer function is given by (28) and (29) for the integer and fractional case, respectively

Obtaining the circuit transfer function of fractional order is part of the transfer function of the capacitor voltage (integer order) and replaces the exponent of the product (ts), initially 1, y is consistent with the Cole model (Cole, 1940), and gives the values of y as 1 (integer case) and 0.8 (fractional case). Thus, the generalized transfer function obtained. The simulation time was 55.164000 seconds, on a computer using Intel Core 2 Duo, 1.8 GHz, 2.99 GB of RAM.

Figure 6, shows the system simulation, with the following values for R₂ = 0.1, R₄ = 0.6, R₃ = 0.4, C₁ = 0.1, C₂ = 0.1, C₁ = 0.1, C₂ = 0.1, C₃ = 0.3, all per unit. Equation (25) comprises fractional derivatives of the three capacitors, and has several cases depending on the equation you want to split (capacitor 1, 2, 3 or combinations exist). In Figure 6, we find that the fractional exponent is y = 0.95 for the differential equation (depending on the capacitor 1) and other equations are of integer order. This figures present the Full Nyquist plot (real and imaginary part for -∞ < ω < ∞) and the Bode plot (frequency response).

Figure 7, shows the simulation for a fractional exponent y = 0.95, taking the differential equation 1 (depending on the capacitor 1) and differential equation 3 (depending on the capacitor 3), β = 0.95. Figure 5 shows the full Nyquist plot (real and imaginary parts for -∞ < ω < ∞) and the Bode plot (frequency response).

The simulation times for Figures 6 and 7 were 18,437 seconds and 18,578 seconds, respectively, using an Intel computer Core 2 Duo, 1.8 GHz, 2.99 GB of RAM.

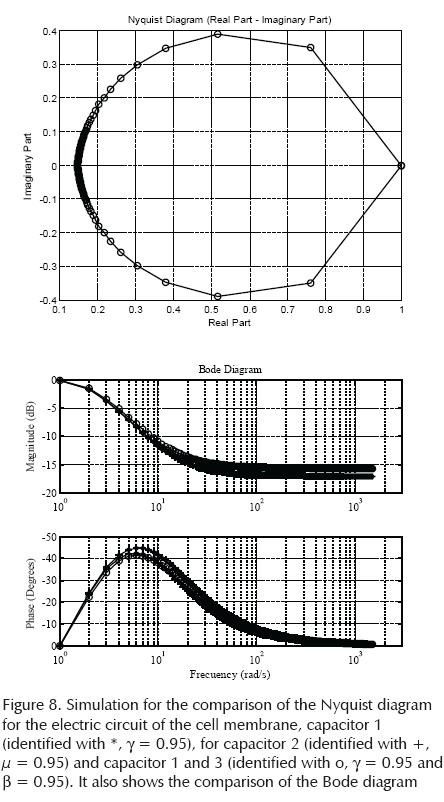
Figure 8, shows the simulation for capacitor 1 (identified with *, y = 0.95), for capacitor 2 (identified with +, μ = 0.95) and capacitor 1 and 3 (identified with o, y = 0.95 and β = 0.95). The full Nyquist plot (real and imaginary parts for -∞ < ω < ∞), has good sensitivity in differentiating the three spectra in comparison with the diagram or Bode (frequency response).

 

Discussion and Conclusions

The study of fractional-order circuits and their technological implications is definitely an emerging area of interdisciplinary research. The study of fractional-order circuits can revolutionize the way we study electrical engineering, and biomedical applications are of particular importance. There is no reason why we should continue modeling and designing systems and circuits in the integer order. The results also suggest that the equivalent circuital representation of biological systems can be used to model the electrical response or frequency response transfer function of an equivalent electrical circuit, the description of bioelectric phenomena, since, as shown in Figure 8, the Bode and Nyquist plots are sensitive to differentiate and characterize the behavior of various biological equivalent circuits.

 

Conclusions

Fractional calculus has been used successfully to modify many existing models of physical processes. The representation of equivalent models in integer order derivatives provided a good approximation of the bioelectric response of the model, however, with the formal introduction of fractional calculus to the study of fractional derivative systems, we have a better approximation of this response, this is due to the nature of fractional calculus and the fact that the systems described by these equations have infinite memory. The representation of the Cole model to describe biological systems has a foundation based on fractional order differential equations. Because of this it is expected that the electrical equivalent model representation of both cellular circuits as action potentials and biological tissues have a bioelectrical response more accurate than could be obtained with the modeling of integer order differential equations, using the quality of regular operators is local, while fractions are not local and incorporated into modeling the effects of memory and contributions of many spatial scales naturally. In the modeling of cellular systems and biological processes are taken into account regular (i.e., follow classical physical laws), but the medium is complex, not only because it is not homogeneous in the classical sense, but also because the medium is broken down more or less random in highly heterogeneous components with very different scales.

Gomez et al. (2010a) presents an analysis and modeling of electrical impedance spectra applied to the study of experimental data of blood tissue and its main components: red, white and plasma. Using electrical circuit theory yields the transfer functions and Bode plot and Nyquist, and Gomez et al., (2010b) presents the theoretical representation using RC circuits of bioelec-trical conduction in a multilayer biological system. In particular, an equivalent circuit type skin: epidermis, dermis and subcutaneous tissue. Representation in Bode and Nyquist diagram is obtained to differentiate the layers of the equivalent circuit, of interest in both studies is the analysis of the representation of equivalent electrical models described in fractional differential equations as it is expected that these have a more accurate response than the bioelectrical obtained with the modeling of integer order differential equations, building on quality that the non-local fractional operators give, and incorporating into the model the effects of memory and contributions of many spatial scales, naturally. In the modeling of cellular systems and biological processes regular (i.e., follow classical physical laws) are taken into account, but the medium is complex, not only because it is not homogeneous in the classic sense, but also because the medium is broken down more or less randomly into highly heterogeneous components with very different scales.

This description would allow a better understanding of bioelectric processes arising in these systems.

 

Acknowledgements

Francisco Gomez is grateful for the support given by CONACYT through the doctoral scholarship granted.

 

References

Casona-Román M., Paul-Torres S., Casanova-Bellido M. Bases físicas del análisis de la impedancia bioeléctrica. Vox pediátrica, volume 7 (issue 139), 1999:143.         [ Links ]

Cole K.S. Permeability and Impermeability of Cell Membranes for Ions. Proc. Cold Spring Harbor Symp. Quant. Biol., volume 8 (issue 110), 1940:122.         [ Links ]

Debye P. Polar Molecules, New York, Dover, 1945.         [ Links ]

Diethelm K., Ford N.J., Freed A.D., Luchko Y. Algorithms for the Fractional Calculus: A selection of Numerical Methods. Comp. Meth. in Appl. Mech. and Eng., volume 194 (issue 743), 2005:773.         [ Links ]

Dorf-Svoboda. Circuitos eléctricos, 6 ed., Alfaomega, December 2000.         [ Links ]

Gómez-Aguilar F., Bernal-Alvarado J., Córdova-Fraga T., Rosales-García J., Guía-Calderón M. On the Construction of Models for electrical Conduction in Biological Tissues, on: Brandan M.E., Herrera-Martínez F., Ramírez-R V., Rodríguez Villa-fuerte M., Eds., AIP Conf. Proc., USA (issue 1310), 2010: 73-76.         [ Links ]

Gómez-Aguilar J.F., Bernal-Alvarado J.J., Rosales-García J.J. Guía-Calderón M., Córdova-Fraga T., Aquino-Modesto S., Hernández-Cabrera F., Palomares-Anda P. Caracterización eléctrica de tejido sanguíneo mediante función de transferencia. Acta Universitaria, volume 20 (special issue 3), December 2010.         [ Links ]

Gutiérrez R.E., Rosário J.M., Machado J.T. Fractional Order Calculus: Basic Concepts and Engineering Aplications, Hindawi Publishing Corporation, Mathematical Problems in Engineering, volume 2010, March 2010.         [ Links ]

Machado J.T. A Probabilistic Interpretation of the Fractional-Order Differentiation. Fractional Calculus and applied Analysis, volume 6 (issue 1), 2003: 73:80.         [ Links ]

Machado J.T., Jesus I.S., Galhano A., Cunha J.B. Fractional Order Electromagnetics. Signal Processing, volume 86 (issue 10), 2006: 2637-2644.         [ Links ]

Magin R.L., Ovadia M. Modeling the Cardiac Tissue Electrode Interface Using Fractional Calculus. Journal of Vibration and Control, volume 14 (issues 9-10), 2008: 1431:1442.         [ Links ]

Podlubny I. The Laplace Transform Method for Linear Differential Equations of the Fractional Order, Tech. Rep., Slovak Academy of Sciences, Institute of Experimental Physics, 1994.         [ Links ]

 

Citation for this article:

Chicago citation

Gomez-Aguilar, Francisco, Juan Rosales-Garcia, Manuel Guia-Calderon, Jesus Bernal-Alvarado. Analysis of Equivalent Circuits for Cells: A Fractional Calculus Approach. ingenieria, investigation y Tecnologia, XIII, 04 (2012): 375-3B4.

ISO 690 citation

Gomez-Aguilar F., Rosales-Garcia J., Guia-Calderon M., Bernal-Alvarado J. Analysis of Equivalent Circuits for Cells: A Fractional Calculus Approach. ingenieria, investigation y Tecnologia, volume XII (issue 4), October-Dicember 2012: 375-3B4.

 

About the authors

Francisco Gómez-Aguilar. He obtained a Masters degree in Electrical Engineering from the Faculty of Mechanical Electrical and Electronics Engineering, University of Guanajuato, specializing in Instrumentation and Digital Systems. He is currently studying his PhD in the Department of Engineering Physics, Division of Science and Engineering Campus León, University of Guanajuato. His interests are bioelectromagnetism, mathematical modeling of biological systems, numerical methods applied to engineering, and fractional calculus.

Juan Rosales-García. He obtained his Doctor of Science degree at UAM Iztapalapa. He currently works in the Department of Electrical Engineering, Division of Engineering, Campus Irapuato, Salamanca, University of Guanajuato. His interests are electromagnetic effects in biological systems and fractional calculus.

Manuel Guía-Calderón. He obtained his Masters degree in Electrical Engineering at the Faculty of Mechanical Electrical and Electronics Engineering, University of Guanajuato, specializing in Instrumentation and Digital Systems. He currently works in the Department of Electrical Engineering, Division of Engineering, Campus Irapuato, Salamanca, University of Guanajuato. His interests are electromagnetic effects in biological systems, numerical methods applied to engineering and fractional calculus.

Jesús Bernal-Alvarado. He obtained his Doctor of Science degree at the University of Guanajuato. He currently works in the Department of Engineering Physics, Division of Science and Engineering Campus León, University of Guanajuato. His interests include electrical impedance spectroscopy and mathematical modeling of biological systems.