1 Introduction
Since the arising of the original proposal of quantum dots technology for quantum computation [1], a number of studies on the subject testing the consistence of the model have been made [2,7]. It is worth emphasizing that a relevant technological application of quantum dots is the concerning to revolutionary TV displays [8-9]. In order to improve the technology it results important to study the gates which are a basic ingredients of this one.
So far the common quantum dots studies employed approaches have considered mainly systems of one and two electron dots. However, it is worth mentioning that in Refs. [5,10] the study of systems composed by many-electron dots have also been included. In fact, in Ref. [5] it has been pointed out that many-body interaction arise when there are more than two electron spins in a computer. Through an approach based on an effective Hamiltonian, in Ref. [5] a system of three and four quantum dots were considered. From such an approach, important observations about contributions to decoherence from the many-body interactions have been done.
One of the main achievements of [5] is the calculation of the exchange interaction through the use of an harmonic oscillator confinement potential of the electron dots. However, such a confinement potential of an electron dot is not a realistic while in the original quantum dot model, the quantum dot confinement is almost complete and this includes scarce tunneling.
On the other hand, it is worth mentioning that the exchange interaction among three and four electron dots induces a CCNOT (Toffoli) [11] and CCCNOT gates respectively, however in Ref. [5] such an gates were not considered. In the present work we point out that the exchange interaction among three and four electron dots induces a CCNOT and CCCNOT gates which change one qubit if the each one of the rest of the control qubits have a value of one.
In order to be more realistic than Ref. [5], in the present approach it is employed a confinement potential of an electron dot which consist of a very high potential well of approximated length equal to one nanometer1.
With such a potential, we calculate the respective times of execution of CCNOT and CCCNOT gates as a function of the coupling constant between the spins. It is worth mentioning that the present approach is both a natural extension and refining of the work done in Ref. [5].
The Hamiltonian that we are employing is:
where V(r) is the confining potential. The 2n basis states are given by:
where
If one assumes that the effective spin operator Hamiltonian (H
spin) has rotation, inversion, and exchange symmetry, considerable
information is extracted from it. In particular, it can be concluded that this is a
function of
where the expansion coefficients Li(i=1,
2, ...) are real constants with dimensions of energy. The information on
Li can be extracted easily by employing the
eigenstates of
If we equate the two expressions
2 Proposal
2.1 Case n = 3 qubits
Through Eq. (1) and a simple manipulation of the results of Ref. [5] it is obtained that:
where the coefficients
In order to estimate the time of execution of the CCNOT (Toffoli) gate 2 it is necessary to calculate the
transition frequencies between the states
In this way, the approximation for the execution time of the Toffoli gate is given by:
where use has been made of Eqs. (4) and (5). In order to calculate the six matrix
elements appearing in Eq. (6), we are using the well known result that the
scalar product is invariant under rotations. The later means that
In order to determine L1, let us consider the
following vertices of an equilateral tetrahedron contained in the
XY plane A = (0,0,0), B =
(ℓ,0,0), C = (ℓ,ℓ,0), and
D = (0,ℓ,0) containing a quantum dot each of
them. Furthermore, we are assuming that the present device is such that
From the above considerations, the Hamiltonian turns out to be:
In order to fix the structure of the confining potential V(r) of the Hamiltonian H, we note that according with the quantum dots model [1], an electron-dot is almost completely confined to a circle of radius of the order of three orders of magnitude the electron's Compton wavelength L ~ 10-9m[12]. Let us observe that the potential employed in [5] does not account for a realistic strict confinement of the electron-dots.
By the above reason, in the present work we are employing a very high rectangular potential well of longitude ~ L which has the form:
Where
for ξ = A, B, C, D and
providing that the Coulomb interaction between the electron-dots is neglected. In
the present work, we are considering only the case
Consequently, with a confinement potential of a very high square well potential, the exchange interaction must be both small and proportional to the transmission coefficient through the walls. In other words, we are assuming that the exchange interaction J = 2L1 is such that, it results simpler to calculate J in this way than with the use of Eq. (3):
where the reflection coefficient of the electron-dot against the wall is [13]:
Being
and T is the transmission coefficient of the quantum dot
electron through the walls of the potential. It results convenient to define the
exchange energy J of Eq. (11) in units of the height of the
potential well which is
where

Fig. 1 The exchange energy of Eq. (13) as a function of
xb in the range
Substitution of (13) in (7) yields:
The above expression predicts that when the height of the box is very high i.e.
On the other hand, in Ref. [14] it has been suggested that the
decoherence times in quantum dots technologies are typically ~
10-7s. In Figure
1 is plotted
On the other hand for small enough values of xb and
T0, the above times of execution become small,
making then the computer more efficient for processing the information. Ideally,
one must have that
The scale of time 10-7s is the estimated decoherence
time of the electron-dots [14]. We note from Eqs. (7, 10, 11) that in
the general case when the three quantum dots are hyper excited i.e.
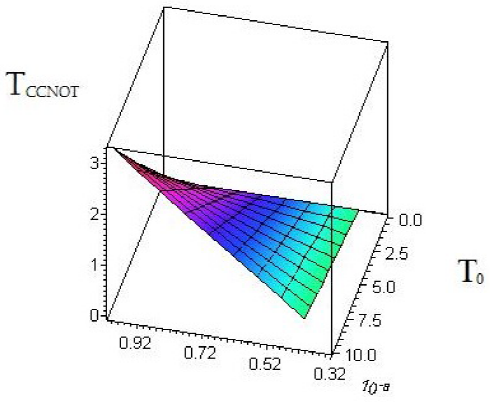
Fig. 2 Time of execution of the CCNOT gate as it is given by Eq. (14) as
a function of xb and
T0 in the range
The later can be explained by saying that when the quantum dots are excited then there will be tunneling effects allowing the necessary interaction between the three parties for executing efficiently the CCNOT gate diminishing with this its execution time.
2.2 Case n = 4 qubits
The approximated expression for the time of execution of the CCCNOT gate 3 is related to the transition
frequencies between the states
where Hspin is given by Eq. (1). Thus, if both the confinement potential of the four quantum dots is given by Eqs. (8) and (9) and we neglect the respective Coulomb interaction then the total energy of the four electron-dots system is given by:
By assuming that
In Figure 3 it is plotted
3 Conclusions
We have studied a systems composed of several quantum dots within an approximated architecture where the Coulomb-like interaction among them can be neglected. By the characteristics of the original electron dot model, the figure of merit is the nature of the confining potential. It is worth mentioning that in the original quantum dot model, the confinement is almost total with scarce tunneling towards outside the region of confinement.
For the above reason in the present work we employ a very high rectangular potential well. Due that the original quantum dot model of Loss and DiVincenzo works in the range of MeV, consequently we have assumed that the confinement potential has a length of the order of one nanometer. We remark that the exchange interaction between the quantum dots induces both CCNOT and CCCNOT gates.
Furthermore, in the present paper a soft tunneling is accounted to consider a not very excited states. Let us observe that a soft tunneling is necessary in order to execute a quantum logic gate. The above is due that with a soft tunneling of the electron dots, they can communicate each other through entanglement which is a necessary ingredient for an exponential speeding up of the processing of the information.
In such a situation the system of quantum dots can execute efficiently the respective quantum gates. The above argument is employed as a basis for the calculation of the times of execution of the CCNOT and CCCNOT gates. It is worth mentioning that the present estimation of such a times is not performed through the use of Eqs. (2) and (3) which involve a cumbersome calculations. Instead we employ both symmetry and probabilistic considerations given by Eq. (11). We have found that allowing a soft tunneling of the dot electrons through the walls of the potential the times of execution of both the CCNOT and CCCNOT gates are drastically small.











 text new page (beta)
text new page (beta)



