1 Introduction
Among the different data mining tasks, classification is appeared as revolutionary task. Classification problems occur when we have to allocate an object in specific group or class on the base of their features or attributes. Classification task depends on two phases.
First phase is to construct the model, which consists of precogitated classes group. Second phase is to classify the unknown objects. The impact of classification task can be viewed in real life phenomena’s such as stock exchange [1], marketing [2], leukemia classification [3], EMG classification [4] gait type classification on inertial sensors data [5] and health care data classification [6].
From last few decades, a variety of models have been developed for data mining. Statistical and artificial neural network models are prominent models. With the passage of time, artificial neural networks (ANNs) have gained much popularity as useful alternative of statistical techniques and due to having the variety of applications in real life [7]. MLP is type of ANNs, which consist of input, hidden and output nodes. In MLP each node is connected with other node in next layer to make connection between them. To train the MLP, different learning algorithms have been used with back propagation such as adaptive momentum to improve gradient descent accuracy [8] and Levenberg Marquardt for classification task. MLP was used to find missing values in data [9], fault detection in gearbox [10], pathological brain detection [11] and power quality disturbance [12].
MLP has large number of applications, meanwhile, MLP has also some drawbacks such as; firstly, multilayer structure causes increase in computational work by stuck in local minima. Secondly, it cannot be used for unsupervised learning. Thirdly, MLP was unable to make high combination of inputs to tackle nonlinear high dimensional problems. To overcome the nonlinear higher order dimensional problem, Chebyshev Multilayer Perceptron (CMLP) was proposed [13]. In this neural network, Chebyshev polynomials based functional expansion layer was introduced to confront high dimensional nonlinear problems. Chebyshev polynomials were used to make standard MLP an efficient tool to perform different types of data mining tasks. This network has been used for classification task.
In this paper, two functional expansions were introduced with MLP such as Shifted Genocchi polynomials and Chebyshev Wavelets. The reason behind using these expansions is well explained in section 2. Simulation results were compared with CMLP based on five evaluation measures.
The contributions made by this study are as follow:
- We proposed Shifted Genocchi Polynomials and Chebyshev Wavelets based Multilayer Perceptron for classification.
- The properties of Shifted Genocchi polynomials such as; firstly, less number of terms as compared to the shifted Chebyshev, Legendre and Chebyshev polynomials, which means that with increasing degree of polynomials, the number of terms also increases. Secondly, the coefficients of individual terms in shifted Genocchi polynomials are smaller than the coefficients of individual terms in the classical orthogonal polynomials. These properties encourage us to implement these polynomials as functional expansion.
- The properties of chebyshev wavelets such as; orthonormality, compact support and function approximation with different resolutions made this proposed model novel, where these wavelets are used as functional expansion.
- A comparative analysis of proposed models with CMLP was completed using five datasets. The performance of all models was verified in terms of five evaluation measures.
The remainder of this paper is organized as follows. Section 2 describes a brief about proposed Models. The experimental design used in this work is discussed in section 3. In section 4 we present the results and discussion. Finally, the conclusion is given in section 5.
2 Functional Expansions Based Multilayer Perceptron Neural Network: Proposed Models
This section describes about functional expansions based proposed models with their network structure.
2.1 Shifted Genocchi Multilayer Perceptron
Functional expansion plays a vital role to make high combination of inputs. These expansions are based on basis functions and selection of basis function is very important task, because basis functions are selected according to the nature of the problem. According to approximation theory, usually orthogonal polynomials are considered as good approximates such as Chebyshev orthogonal polynomial. Researchers have used different types of basis functions as functional expansion such as Chebyshev polynomials, Laguerre polynomials and Legendre polynomials [14].
We introduce shifted Genocchi (non-orthogonal) polynomial, which is better approximation property as compared to orthogonal polynomials due to certain characteristics. Firstly, Shifted Genocchi polynomials have less number of terms than the shifted Chebyshev, Legendre and Chebyshev polynomials, which means that with increasing degree of polynomials, the number of terms also increases. For example, on third order degree Shifted Genocchi have three numbers of terms and shifted Chebyshev have four numbers of terms leading to less computational work. Secondly, the coefficients of individual terms in shifted Genocchi polynomials are smaller than the coefficients of individual terms in the classical orthogonal polynomials.
Since the computational errors in the polynomial are related to the coefficient of individual terms, the computational errors are less by using shifted Genocchi polynomials. Motivated from above properties, Shifted Genocchi polynomials are proposed. The equation to derive the polynomials is given in Equation 1 as follows:
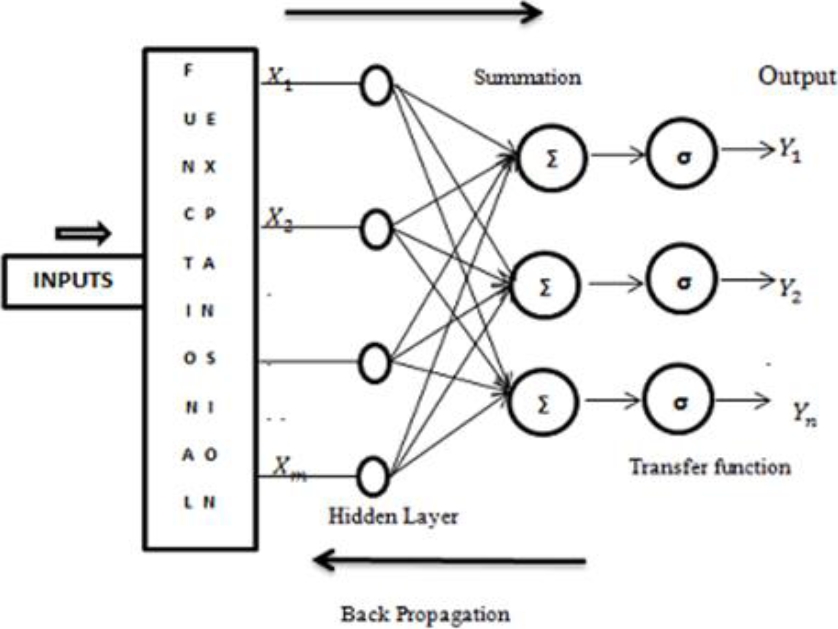
where SG 0(t), SG 1(t) are the first and second polynomials respectively. SG 1(t) is the analytical form of n th shifted Genocchi polynomials and ‘G’ is the Genocchi number. The network structure is presented in Figure 1, where, X 1, X 2 … X m are the inputs and Y 1, Y 2 … Y n indicates the output of the neural network.
2.2 Chebyshev Wavelets Multilayer Perceptron
As discussed earlier that, basis functions have very important role as functional expansions to tackle the high dimensions nonlinear problems. Here, Chebyshev wavelets which are derived from Chebyshev polynomials are also used as functional expansion. These wavelets were derived from the dilation and translation of single function. The properties of orthonormality, compact support and due to functions approximation with different resolutions in Chebyshev wavelets made them better as compared to Chebyshev polynomials and Shifted Genocchi polynomials [15]. To understand the reason behind using wavelets, we have discussed three cases regarding to these properties.
Case 1. Orthonormality
Two vectors in an inner product space are orthonormal if they are orthogonal and unit vectors. In more simple way, “A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length”. An orthonormal set which forms a basis is called an orthonormal basis. In case of functional expansion, the constant of expansion for the wavelets is more accurate due to orthonomality property as compared to polynomials, where constant of expansion is not more accurate due to orthogonality.
Case 2. Compact Support
In mathematics, compact support can be defined as, “A function has compact support if it is zero outside of a compact set”. For example, set ‘A’ has a compact support means that it has support which is closed and bounded. On the other hand, the function f:x → x 2 in its entire domain (i.e., f:R → R +) does not have compact support. In case of wavelets as functional expansion, wavelets with compact support have more advantage over that without compact support, because function approximation within the interval will be more accurate as compared to out of the interval.
Case 3. Function approximation with different resolution
In case of functional expansion, for wavelets we can maintain the degree of governing polynomial and increase the resolution by increasing values of k(integer). Therefore, we have the advantage of seeing the values of expansion at different intervels. For polynomials, just with the maintenance of degree, we cannot see the advantage of increase in accuracy.
Therefore, with the advantages of above three properties, we have proposed Chebyshev Wavelets based MLP (CWMLP) in this study. In this proposed method, these wavelets were used as functional expansion for more accurate classification. Chebyshev wavelets can be derived as following.
Chebyshev wavelets for piecewise polynomial spaces can be construct on interval [0, 1].
Some notations are needs to be introduce for this work, such as:
N 0: = {0,1, …}, N denotes the natural numbers and Z δ : = {0,1,2, …, δ − 1} for a positive integer δ.
For an integer δ > 1, contractive mappings is considered on I: = [0, 1]:
Mappings {ψ v } clearly fulfil the following properties:
Let G 0 is finite dimensional linear space on [0, 1], which is spanned by Chebyshev polynomials:
where M ∈ N and T m (x) is the polynomial of m-order, namely:
It is known that Chebyshev polynomials T
m
(x) are orthogonal w.r.t weight function
For construction of orthonormal base of L 2[0, 1], we define for each v ∈ Z δ an isometry R v on L 2[0, 1]:
Starting from G 0 space, we define the sequence of spaces {G k k ∈ N 0} via the recurrence relation:
where
Generally denotes the direct sum of A and B spaces:
and
Now by constructing the orthonormal base for each space G k :
where:
is an orthonormal base of space G 0 and for all f(x) ∈ L 2[0, 1].
Then the set of {ψ (k) n,m (x) | n = 1,2, …, δ k , m ∈ Z M } forms an orthonormal base for space G k w.r.t weight function w n (x) where:
For δ = 2, k = 1 and M = 3, Chebyshev wavelets on interval [0, 1) are as follows:
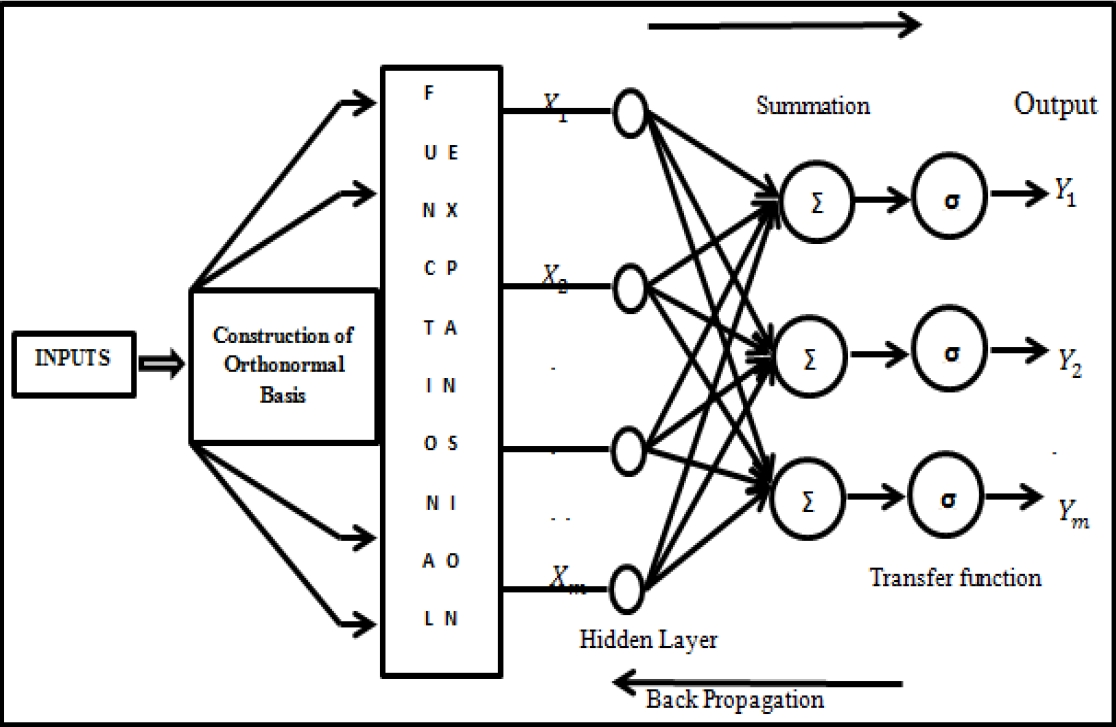
The network structure of Chebyshev Wavelets Multilayer Perceptron (CWMLP) is depicted in Figure 2, where, X 1, X 2 … X m are the inputs and Y 1, Y 2 … Y n indicates the output of the neural network.
The construction of orthonormal basis box was used to construct the wavelets because without constructing orthonormal basis wavelets cannot be derived. Functional expansion layer is the representation of high combination of inputs.
2.3 Correct / Wrong Classification Examples
To check that, whether the both proposed techniques such as SGMLP and CWMLP can classify the data correctly or not firstly we have considered the XOR binary dataset. The summary of the dataset is given in Table 1.
This dataset is too small to train and test the performance of proposed techniques therefore we have taken twenty times of this dataset for the experiments. The simulation results are shown inTable 2.
Table 2 XOR dataset simulation results
| XOR (Dataset) | SGMLP | CWMLP |
|---|---|---|
| Training set | 92.38 % | 95.97% |
| Testing set | 94.16% | 98.73% |
| When X 1 = 0, X 2 = 0 | 100% | 100% |
| When X1 = 0, X2 = 1 |
96.02% | 98.89% |
| When X 1 = 1, X 2 = 0 | 100% | 100% |
| When X 1 = 1, X 2 = 1 | 97.25% | 98.46% |
| Average | 93.27% | 97.35% |
The simulation results of training, testing sets and all samples training results using SGMLP and CWMLP are summarized in Table 2. The results have shown that, SGMLP has performed 92.38 % and 94.16% accuracy on training and testing dataset respectively.
On the other hand, the performance of CWMLP was found 98.73% on testing set, which is more accurate on XOR binary dataset which means that, both models have ability to perform better on multi-class dataset due to addition of functional expansional layer for data Classification. Moreover, these simulation results have also shown that, both techniques have correctly classified the binary dataset.
2.4 Basic Definitions
This section comprises of some basic definitions that are related to this research work.
Imbalanced Datasets: Imbalanced datasets are a special case for classification problem where the class distribution is not uniform among the classes. Typically, they are composed by two classes:
The majority (negative) class and the minority (positive) class.
Balanced Datasets: A balanced dataset is a set that contains all elements observed in all time frames.
Supervised Learning: All data is labeled and the algorithms learn to predict the output from the input data.
Unsupervised Learning: All data is unlabeled and the algorithms learn to deduce structure from the input data.
3 Experimental Design
This section explains step by step about experimental design of all techniques. The datasets, evaluation measures, data pre-processing and network topology of comparison and proposed techniques were discussed.
3.1 Data Collection
The data sets for classification analysis, which is the requisite input to the models, are obtained from UCI Repository1 and KEEL datasets2 [16, 17].
Here the UCI Machine Learning Repository is a collection of databases, domain theories, and data generators that are used by the machine learning community for the empirical analysis of machine learning algorithms and KEEL (Knowledge Extraction based on Evolutionary Learning) is an open source (GPLv3) Java software tool that can be used for a large number of different knowledge data discovery tasks.
We have collected five datasets namely, Ringnorm, Banana, Titanic, Breast Cancer and Bank Note Authentication datasets. Each dataset was divided into two parts; training set and testing set. The data ratio of 70% and 30% was set for training and testing respectively. The details of the used data sets are described in Table 3.
3.2 Evaluation Measures
The performance of comparison and proposed models is evaluated on the base of five evaluation measures. The formulae of evaluation measures is given in Table 4, where Tp, Tn, Fp and Fn are the true positive, true negative, false positive and false negative values respectively.
Table 4 Description of Evaluation Measure
| Evaluation Matrices | Mathematical Equations |
|---|---|
| Accuracy |
|
| Sensitivity |
|
| Specificity |
|
| Precision |
|
| F-Measure |
|
| Epochs | 1000 |
| Area Under the Curve |
|
| Mean squared error |
|
3.3 Data Pre-Processing
Data transformation is the process to normalize each data set into useful data. Data was normalized to the range [0.2, 0.8] and minimum and maximum normalization method was applied as given in Equation 2:
where
3.4 Training and Network Topology
The proposed models topology of SGMLP and CWMLP is shown in Table 5. Settings were selected empirically.
Table 5 Network Topology
| Setting | Value |
|---|---|
| Activation Function | Sigmoid function |
| Genocchi Polynomial degree | 3 |
| Stopping Criteria | Maximum no. of epochs=1000 |
| Learning rate Momentum Learning Algorithm |
[0.1-0.3] [0.3-0.9] LM back propagation |
Levenberg Marquardt (LM) back propagation was used as learning algorithm with all techniques.
4 Results and Discussion
This section consists of simulation results of comparison and proposed models. The experiments were performed 10 times and then average was taken to obtain verified results.
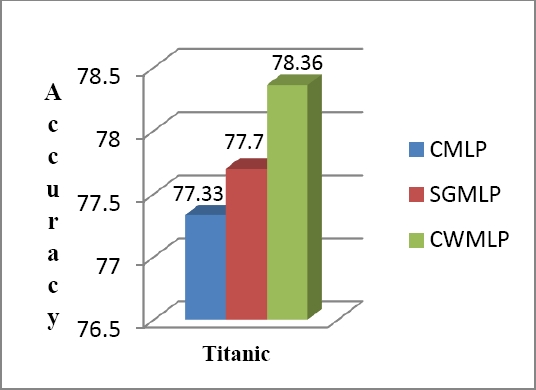
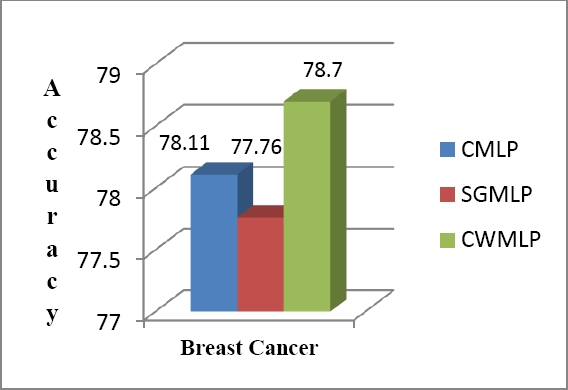
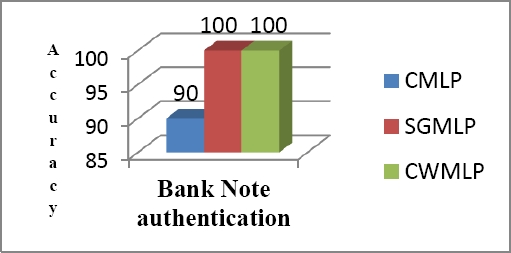
1000 number of iterations was taken in all experiments. Levenberg Marquardt back propagation was used as learning algorithm in all models. Classification accuracy of all models in all datasets was shown in bar graph from Figure 3 to Figure 7.
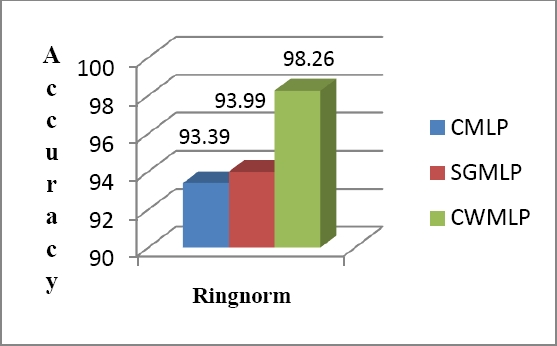
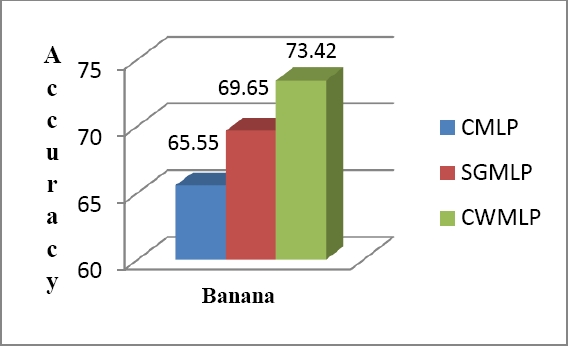
The accuracy is used to check the overall effectiveness of the techniques. It can be seen that, CWMLP performance was better on Ringnorm and Banana datasets, whereas, CWMLP perform slightly better on Titanic dataset as compared to SGMLP and CMLP.
The reason behind these significant results is that, the proposed solution helps CWMLP to raise and find more appropriate settings during the training which helps to enhance the classification performance for network. This better performance is also due the reason that, Chebyshev wavelets can generate more numbers of basis functions using same degree as compared to Shifted Genocchi polynomials based MLP technique that help to generate more enhanced values with small coefficients and reduced the computational task. Meanwhile, it seems that SGMLP was not fully supported by parameter settings that cause less improvement with CWMLP.
In case of Brest Cancer dataset, SGMLP performance was lower than the CMLP, but CWMLP perform better than both of the techniques with 78.70% classification accuracy. This is due to the reason that, sometime due to the imbalanced dataset, techniques are not able to classify the data correctly. In Bank Note Authentication dataset, CWMLP and SGMLP performance was 100% to classify the data. The same parameters setting and number of epochs are the reason behind the same results on the other hand CMLP performance was found to be 90%. Over all, it can be seen that CWMLP performance was much better than the SGMLP and CMLP on all datasets in terms of classification accuracy.
The best performance with CMLP, SGMLP and CWMLP using the Banana, Titanic, Ringnorm, Breast Cancer and Bank Note Authentication datasets in terms of Sensitivity, Specificity and Precision is shown in Table 6. As it can be noticed from Table 6, CWMLP identify the proportion of positive values (Sensitivity), proportion of negative values (specificity) and selected items, which are relevant (Precision) correctly with higher performance on Bank note Authentication and Ringnorm datasets.
Table 6 Comparison in terms of sensitivity, specificity and precision
| Datasets | Techniques | Sensitivity | Specificity | Precision |
|---|---|---|---|---|
| Ringnorm | CMLP | 93.41 | 93.41 | 93.41 |
| SGMLP | 94.79 | 94.79 | 94.79 | |
| CWMLP | 98.26 | 98.26 | 98.26 | |
| Banana | CMLP | 71.97 | 71.97 | 80.09 |
| SGMLP | 72.54 | 72.54 | 80.71 | |
| CWMLP | 77.08 | 77.08 | 78.95 | |
| Titanic | CMLP | 80.09 | 80.09 | 80.09 |
| SGMLP | 80.65 | 80.71 | 80.49 | |
| CWMLP | 80.77 | 80.79 | 80.77 | |
| Breast Cancer |
CMLP | 74.88 | 72.13 | 70.93 |
| SGMLP | 76.25 | 76.25 | 76.25 | |
| CWMLP | 77.32 | 77.22 | 77.02 | |
| Bank Note Authentication |
CMLP | 90 | 90 | 90 |
| SGMLP | 100 | 100 | 100 | |
| CWMLP | 100 | 100 | 100 |
In Titanic dataset, there is slightly difference between all comparison techniques. In Breast Cancer dataset, SGMLP perform well as compared to CMLP, because Shifted Genocchi can generate more better enhanced inputs due to small coefficient value and less degree, similarly, CWMLP perform slightly high than the SGMLP in terms of Sensitivity, Specificity, and Precision. Over all, it can be seen that CWMLP outperform on all datasets in comparison of SGMLP and CMLP. Bold font was used to prominent the proposed techniques results.
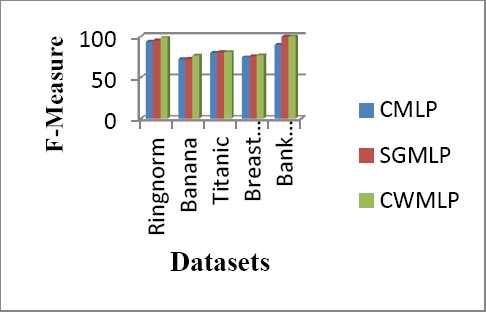
Test’s accuracy was measured by F-Measure. Precision and Sensitivity were used to compute the f1-score. The higher value shows its best, lower value shows its worst. In the Figure 8 bar graph represents the F-Measure results of all the comparison techniques. In Bank Note Authentication, SGMLP and CWMLP gives their best with 100% f1-score as compared to CMLP. After that, in Ringnorm dataset CWMLP perform well with 98.26 % as compare to SGMLP and CMLP.
In Titanic dataset all the comparison techniques score was slightly different from each other. From results we can conclude that, CWMLP performance was much better than the other techniques in terms of F- Measure. On the whole, it can viewed that the performance of CWMLP is much better due to their property of generating more number of small value coefficient based wavelets as compared to other basis functions. Whereas, the enhanced inputs generated by Chebyshev polynomials are not able to reduce the computational complexity of the network.
4.1 Significance Using T-test
To check that how much significant are our proposed techniques, we have applied paired two samples for means t-test in relation of accuracy. We found that, in all datasets SGMLP has shown significance except in Ringnorm dataset when compared with CMLP. Insignificance has caused due to approximately similar high accuracy of both proposed and comparison techniques. In Breast Cancer dataset, SGMLP again remain insignificant due to approximately similar accuracy when compared with CWMLP. In rest of datasets, CMLP remained insignificant in all datasets. The hypothetic value was taken 0.05. If we achieved ‘value < 0.05’ then called as significant and ‘value >0.05’ then called as insignificant.
5 Conclusion
In this paper, two functional expansions based multilayer perceptron models were proposed to tackle higher dimension nonlinear problems. The concept of adding new functional expansion layer in MLP using Shifted Genocchi polynomials and Chebyshev wavelets were proved much better. It is due to reason that, the number of enhanced inputs generated by these polynomials and wavelets are small in values and less computational as compared to CMLP. Moreover, Chebyshev wavelets have ability to produce more number of basis functions on the same degree as compared to Shifted Genocchi and Chebyshev polynomials. Which is helpful to increase the accuracy of the classifier.
CWMLP and SGMLP were experimentally trained and tested on five benchmarked data sets, which were taken from UCI repository and KEEL datasets. The performance of the proposed models indicates their validity for classification task. The evaluation measures performance show that the SGMLP and CWMLP has better performance in terms of accuracy, sensitivity, specificity, precision and F-Measure over CMLP. Overall, CWMLP performance was outstanding as compared to rest of the techniques.
Similarly, t-test clearly validates the significance of proposed techniques over the benchmarked approaches.











 nova página do texto(beta)
nova página do texto(beta)